A 2020-ban bevezetett NAT és kerettanterv következtében megváltoztak az érettségi követelmények is. (A változásokkal – egy ötrészes cikksorozat keretében – részletesen foglalkoztunk az Érintőben is (27–31. szám) 2023 márciusától kezdve.) A változások miatt a 2024. májusi érettségi feladatsorokat a megszokottnál is nagyobb érdeklődés övezte, így érdemesnek tűnik a vizsga után visszatekinteni az eredményekre, különös tekintettel azokra a feladatokra, amelyek valamilyen szempontból újak, újszerűek voltak a feladatsorokban.
Az alábbi elemzés gerincét az iskolák által nyújtott önkéntes adatszolgáltatás adatainak elemzését tartalmazó, 2012 óta minden évben elkészített összeállítás idei változata adja.
A kétszintű érettségi szoftverben a matematika vizsgadolgozatok esetében az I. és II. rész pontszámait szükséges csak rögzíteni, így korábban nem álltak rendelkezésre részletes adatok a feladatonkénti pontszámok országos eloszlásáról. Ezen próbáltunk változtatni, amikor először a 2012-es tavaszi vizsgaidőszakban az Oktatási Hivatalon keresztül az iskolákat önkéntes adatszolgáltatásra kértük: gyűjtsék össze és küldjék el a vizsgázók pontszámait feladatonként.
Idén már tizenharmadik alkalommal végeztük el ezt a kutatást, és azóta összesen több mint 200 ezer középszintű vizsgázó által megoldott 234 feladat, illetve közel 13 ezer emelt szintű vizsgázó által megoldott 117 feladat részletes pontszámai állnak rendelkezésre. 2018-ban a kutatás tovább bővült: az iskolákat arra kértük, ha idejük engedi, alkérdésenként is rögzítsék a pontszámokat, bár elfogadtuk a feladatonkénti rögzítést is, ha ez nem volt kivitelezhető.
A 2024. május-júniusi vizsgaidőszakban középszinten 64 630-an, emelt szinten 6371-en írták meg a matematika írásbeli érettségit magyar nyelven. E vizsgázók közül 22 307 (34,5%) középszinten és 1539 (24,2%) emelt szinten szereplőről kaptunk részletes adatokat. A minta nagysága idén is lehetővé teszi, hogy a teljes vizsgázói populációra vonatkozóan megbízható következtetéseket vonjunk le, bár az összes vizsgázóra nézve a minta reprezentativitása nem igazolható. A középszintű dolgozatok közül 12 914 (57,9%), az emelt szintűek közül pedig 947 (61,5%) vizsgázó pontszámait alkérdésenként kaptuk meg. Idén is felülreprezentáltak voltak a jobb eredményű dolgozatok: a visszaküldött középszintű dolgozatok átlaga 2,5, az emelt szintűeké pedig 3,9 százalékponttal magasabb az összes vizsgázó átlageredményénél.
Az adatokat az 1. táblázat foglalja össze.
| középszint | emelt szint | |||
| darabszám | átlageredmény | darabszám | átlageredmény | |
| összes írásbeliző | 64 630 | 52,1% | 6371 | 66,6% |
| összes visszajelzett | 22 307 | 54,6% | 1539 | 70,5% |
| ebből alkérdésenként rögzített | 12 914 | 55,0% | 947 | 70,4% |
| ebből alkérdésenként rögzített | 9393 | 54,1% | 592 | 70,6% |
| nem visszajelzett | 42 323 | 50,8% | 4832 | 65,4% |
1. táblázat: A magyar nyelven írt matematika írásbeli vizsgadolgozatok átlageredménye (2024. május)
Az emelt szintű vizsgázók aránya – mind az összes érettségi vizsga, mind a matematika esetében – idén érezhetően növekedett, amit az újonnan bevezetett „kétharmados” szabály is ösztönzött. Ez a szabály kimondja, hogy a középszintű vizsgaeredményt csak kétharmados szorzóval veszik figyelembe az érettségi pontok számításánál. Hasonló mértékű növekedés utoljára 2020-ban volt tapasztalható, amikor bevezették azt a követelményt, hogy a továbbtanuláshoz szükséges legalább egy emelt szintű vizsga. Az emelt szintű matematikavizsgák 8,7%-os aránya azonban továbbra is a magyar nyelv és irodalom után a második legalacsonyabb a „nagy” tárgyak között, és jelentősen elmarad az összes tantárgyi vizsga körében mért 17,5%-os aránytól.
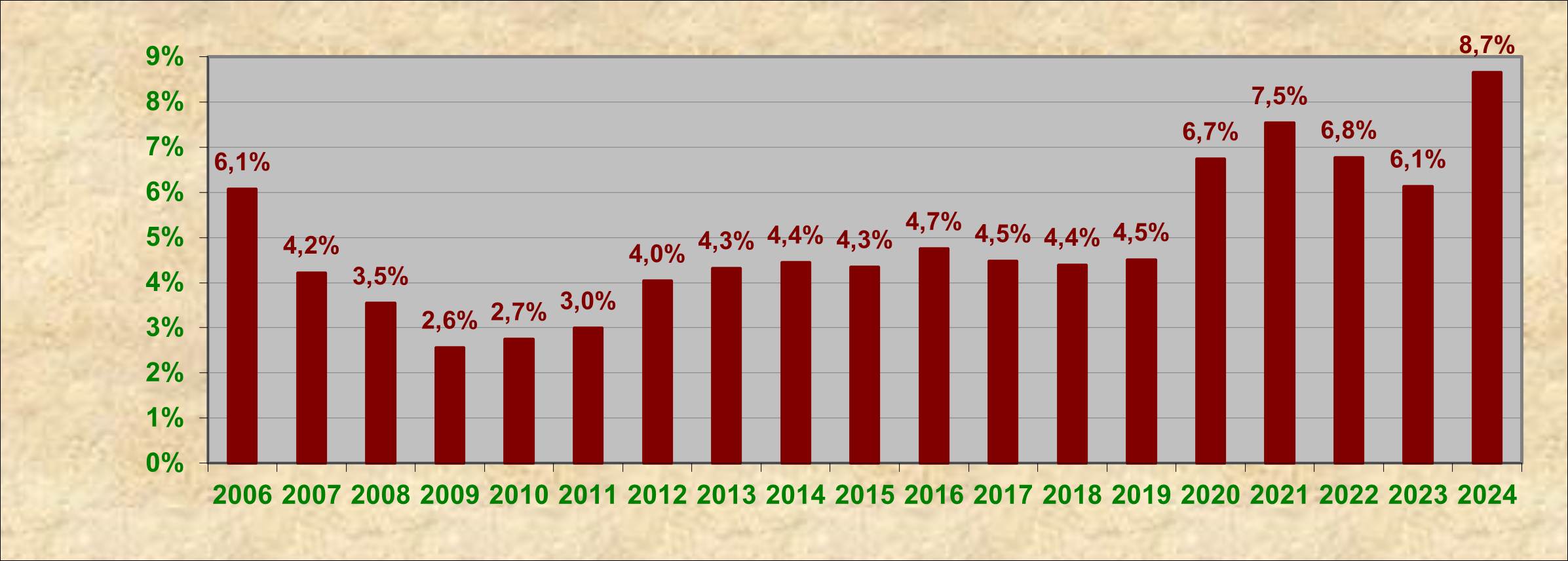1. ábra: A matematikából emelt szinten vizsgázók aránya a tavaszi vizsgaidőszakban (2006-2024)
Az elmúlt 18 év magyar nyelvű középszintű matematika írásbeli feladatsorai között az idei bizonyult a második legmagasabb megoldottságúnak – a tavalyit éppen megelőzve, de a 2022-es év eredménye mögött –, annak ellenére, hogy a végzősöket tanulmányaik során hosszabb ideig érintette a digitális tanrend. A 2007 óta készült összes feladatsor átlagos eredménye 47,8%, míg a 2022-es feladatsoré 53,7%, a tavalyié 51,2%, az ideié pedig 52,1% lett. Az elmúlt három évben kitűzött feladatsorok így a legjobban sikerült dolgozatok közé tartoznak.
Az, hogy az írásbeli vizsga jól sikerült a sokéves átlaghoz képest, azzal is alátámasztható, hogy a 2012-es (10-ről 12 pontra történt) ponthatáremelés óta idén volt a második legalacsonyabb a sikertelen, 12 pont alatti írásbelik aránya (1,3%), csak a 2020-as 0,9%-os arány volt alacsonyabb. (Ez okozhatta azt, hogy 2025 őszén a korábban megszokott létszám körülbelül 60%-a tett középszinten érettségi vizsgát.)
A magyar nyelven írt emelt szintű írásbeli vizsgák átlageredménye 2024-ben 66,6% volt, ami megfelel a sokéves átlagnak. A középszint helyett az új pontszámítási szabályok miatt emelt szintet választó 2-3%-nyi vizsgázó eredménye kis mértékben csökkenthette az országos átlagot mindkét szinten: ők középszinten vélhetően inkább a jobbak közül kerültek volna ki, és jó eredményük hiányzik a középszintű átlagból, emelt szinten viszont jellemzően a kevésbé jók közé tartozhatnak.
Az alábbiakban az egyes feladatok eredményessége az önkéntes adatszolgáltatás során gyűjtött értékekből származik.
Középszint
A középszintű feladatsort itt tekinthetik meg olvasóink.
A javítási-értékelési útmutató itt található.
Miután a középszintű változások túlnyomó része valamely követelmény kikerülését jelentette a korábbiak közül, így kevés újdonságról, illetve annak eredményességéről tudunk beszámolni. A 4-es feladat (statisztikai manipuláció felismerése) és a 15. c) alfeladat (dobozdiagram értelmezése) volt olyan, amilyennel korábban a vizsgázók nem találkozhattak, a többi feladat tulajdonképpen a 2024 előtti feladatsorokban is előfordulhatott volna.
A 4-es feladat volt idén a legsikeresebb feladat (86%-os eredményesség), amit nyilvánvalóan az okozott, hogy meglehetősen egyszerű formában kérte számon a statisztikai manipuláció felismerését. A 15. c) alfeladatban egy diagram alapján négy kijelentésről kellett megítélni azok igazságtartalmát (igaz-hamis-nem lehet eldönteni). Ez a feladat szintén átlagon felüli eredményességet hozott (61%), amiből óvatosan levonható az a következtetés, hogy a vizsgázó diákok alapvetően megismerték és értik a dobozdiagramot (boxplot-diagramot).
| Feladat | Átlag | Kihagy |
| 1. A és B halmaz megadása | 81% | |
| 2. derékszögű háromszög befogója | 82% | |
| 3. négyjegyű pozitív páratlan számok | 70% | |
| 4. statisztikai manipuláció felismerése | 86% | |
5.  |
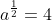70% | |
| 6. számtani sorozat első 6 tagjának összege | 58% | |
| 7. hatszög alapú gúla (csúcsok, lapok, élek) | 73% | |
| 8. szám kétszeresének 2-es alapú logaritmusa | 42% | |
| 9. polgármester-választás | 75% | |
| 10. függvények zérushelye | 64% | |
| 11. 1, 5, 5, 5 átlaga és szórása | 64% | |
| 12. P(három különböző dobás) | 61% | |
| I. rész összesen | 67,8% | |
| 13. a) elsőfokú egyenlet | 76% | |
| 13. b) 1896 és 1956 közös osztói | 53% | |
| 14. a) szabályos tízszög egy belső szöge | 59% | |
| 14. b) szabályos tízszög területe | 39% | |
| 14. c) 2015 átlójú sokszög | 39% | |
| 15. a) éttermi rendelés – lineáris egyenletrendszer | 49% | |
| 15. b) éttermi rendelés – valószínűségszámítás | 44% | |
| 15. c) dobozdiagram | 61% | |
| II/A rész | 52,3% | |
| 16. a) függvények kiválasztása | 40% | 67% |
| 16. b) lineáris függvény | 43% | |
| 16. c) kör egyenlete | 33% | |
| 17. a) habos isler – térfogat | 74% | 24% |
| 17. b) habos isler – átmérő | 48% | |
| 17. c) habos isler – valószínűségszámítás | 28% | |
| 17. d) cukrászdai rendelések | 36% | |
| 18. a) hatpontú gráf | 78% | 10% |
| 18. b) elektromos autó hatótávolsága – számtani sorozat | 61% | |
| 18. c) elektromos autó hatótávolsága – mértani sorozat | 31% | |
| II/B rész | 46,4% | |
| II. rész összesen | 49,0% | |
| Dolgozat összesen | 54,6% |
2. táblázat: Az egyes feladatok eredményessége a középszintű vizsgadolgozatokban (2024)
I. RÉSZ
Az I. rész feladatainak megoldottsága 68%-os volt, ami kissé magasabb a sokéves átlagnál. Míg tavaly és tavalyelőtt csupán egyetlen feladat megoldottsága érte el a 80%-ot, idén (a korábbi trendekhez hasonlóan) ismét három ilyen feladat is volt a feladatsorban. Ezeket a feladatokat a feladatsor „nagyon könnyű” feladatai közé sorolhatjuk.
Nem meglepő módon a legalacsonyabb megoldottságú feladat a 8. feladat lett (és ez az egyetlen, amely az 50%-os megoldottsági szintet sem érte el), ugyanakkor kissé váratlan, hogy a második legalacsonyabb megoldottságú feladat a számtani sorozatokra vonatkozó 6. feladat volt. A 11. feladat megoldottsága átlagosnak mondható, bár érdekesség, hogy a vizsgázók mindössze 1,7%-a kapott rá 0 pontot: a négy egyjegyű szám átlagának kiszámítása a többségnek sikerült, de a szórás kiszámítását már a vizsgázók fele nem tudta megoldani.
II. RÉSZ
A vizsgázók átlagos teljesítménye a II. részben 49,0% volt, ami meghaladja a sokéves átlagot, bár alacsonyabb az előző két év eredményeinél. A II/A rész (52,3%) ismét jobban sikerült, mint a II/B rész (46,4%). A II. részben három feladat megoldottsága haladta meg az 50%-ot, míg egy feladaté 40% alatt maradt.
Kiemelkedő a 13. feladat 63%-os megoldottsága; ennél magasabb értéket 2012 óta csak egyszer (2022-ben, a 15. feladatnál) mértünk. A 14. feladattal kapcsolatban érdekes megfigyelés, hogy a 20% alatti összteljesítményt elérő 1092 vizsgázó 83%-a 0 pontot kapott, és esetükben a feladat megoldottsága 3% alatt maradt, noha egy látszólag nem túl nehéz geometriai feladatról van szó. Ugyanakkor a legjobb eredményt elérők (akik 90% fölött teljesítettek) körében épp ez a feladat bizonyult a legsikeresebbnek a II. rész feladatai közül.
A II/B részben idén is megfigyelhető volt, hogy minél nehezebbnek bizonyult egy feladat, annál többen hagyták ki, vagyis a vizsgázók általában jól mérték fel, mely feladatok megoldásával érdemes foglalkozniuk, és megfelelően használták ki a vizsgaleírás által kínált választási lehetőséget. Ahogy szinte minden évben, idén is szignifikáns különbségek figyelhetők meg a kihagyott feladatoknál: a 17. feladatot kihagyók átlageredménye a teljes feladatsoron 51,4 pont volt, míg a 18. feladatot kihagyók átlaga 59,1 pont. Ez azt mutatja, hogy a II/B részben a viszonylag könnyebb 18. feladatot nagyobb arányban hagyták ki a magasabb pontszámú vizsgázók.
Ez a jelenség nem új, 2013 óta minden évben úgy alakult, hogy a 90% fölött teljesítők az összes vizsgázóhoz képest nagyobb arányban hagyták ki a 18. feladatot. Valószínű, hogy ez azért történik így, mert a kiválóan teljesítők sorban haladva sikeresen megoldják a feladatsor előző részeit, így a 16. és 17. feladatot is, és végül a legutolsó, 18. feladatot hagyják ki.
Az 1–15. feladatokat minden vizsgázónak meg kell oldania, így ebben a közös részben pontosan ismerjük az összes vizsgázó által elért átlagos eredményt, amely idén 54,6% volt. Hasonlóan, ismert az adott választható feladatot megoldó vizsgázók átlageredménye is ebben a közös részben. A két érték hányadosa jól mutatja, hogy a választható feladatot választó vizsgázók átlagos képessége hogyan viszonyul az összes vizsgázó átlagos képességéhez.
A tényleges megoldottságot ezzel a hányadossal korrigálva kapjuk meg a feladat normált megoldottságát, ami pontosabb mérőszámot ad a feladat valós nehézségéről. A 2024-es feladatsorban ezzel a módszerrel számított normált megoldottsági értékek a következők: 36,2% (16. feladat), 43,5% (17. feladat) és 52,7% (18. feladat). A normált megoldottság hitelesebb képet ad a feladatok valódi nehézségéről, bár idén a tényleges és normált megoldottságok között a szokásosnál kisebb eltérések mutatkoztak. (A 2. táblázat a tényleges megoldottságokat tartalmazza, a 16., a 17. és a 18. feladat esetében is 1 százalékponton belül volt idén az eltérés a tényleges és a normált megoldottságok között..)
Emelt szint
Az emelt szintű feladatsort itt tekinthetik meg olvasóink.
A javítási-értékelési útmutató itt található.
Az emelt szintű követelmények lényegében nem változtak meg 2024-ben (a középszintről kikerülő követelmények általában átkerültek emelt szintre, de ezek korábban is az emelt szintű követelmények részét képezték), néhány újdonság a gráfok és a statisztika témakörben jelent meg. A 2024-es feladatsorban ezek közül a 9. a) feladatban kellett az n pontú teljes gráf éleinek a számát felírni, és ezzel kapcsolatos feladatot megoldani.
Néhány sor a szóbeli vizsgákról. A szóbeli vizsgák átlageredménye 2011 és 2019 között nagyon stabil volt: egy szűk, 1,5%-os sávban (75,2–76,7%) mozgott. 2020-ban és 2021-ben elmaradtak a szóbeli vizsgák, 2022-ben pedig jelentős visszaesés történt (70,1%). 2023-ban és idén ismét enyhe javulás volt érzékelhető (72,1%, illetve 72,0%), de a 2020 előtti magasabb értékeket még nem sikerült elérni. Ennek oka lehet a koronavírus-járvány miatt kimaradt jelenléti oktatási időszak, ami hatással lehetett az ebben az időszakban érettségiző diákokra. Továbbá az idei eredményt némileg csökkenthette, hogy egyesek a középszint helyett emelt szintű vizsgát választottak az új felsőoktatási pontszámítási szabályok miatt (ők az emelt szintű vizsgázók körülbelül egynegyedét-egyötödét tehetik ki).
| Feladat | Átlag | Kihagy |
|---|---|---|
| 1. a) logaritmusos egyenlet | 90% | |
| 1. b) exponenciális egyenlet | 83% | |
| 1. c) inverzfüggvény | 48% | |
| 2. a) hétjegyű számok | 66% | |
| 2. b) négyelemű részhalmazok | 57% | |
| 2. c) állítás megfordítása | 62% | |
| 3. a) kockapóker – Sor | 65% | |
| 3. b) kockapóker – Full House vagy Royal | 78% | |
| 3. c) p értékének meghatározása | 56% | |
| 4. a) négyzetben háromszög – területek aránya | 67% | |
| 4. b) négyzetben háromszög – szakaszok hossza | 75% | |
| 4. c) négyzetben háromszög – háromszögek hasonlósága | 52% | |
| I. rész összesen | 68,5% | |
| 5. a) sorozat határértéke | 77% | 24% |
| 5. b) sorozat monotonitása | 66% | |
| 5. c) egyenlet megoldása | 69% | |
| 5. d) integrálszámítás | 85% | |
| 6. a) felülések | 95% | 7% |
| 6. b) Sziget-kör-futás | 60% | |
| 6. c) közepek | 88% | |
| 7. a) homokszemek | 82% | 15% |
| 7. b) homokkupac – térfogat | 93% | |
| 7. c) homokkupac – szélsőérték | 54% | |
| 8. a) kör középpontja, sugara | 91% | 21% |
| 8. b) húrtrapéz magassága, szögei | 80% | |
| 8. c) koordináták | 53% | |
| 9. a) gráf pontjai | 89% | 33% |
| 9. b) doppingellenőrzés valószínűsége | 62% | |
| 9. c) kézfogások | 48% | |
| II. rész összesen | 72,1% | |
| Dolgozat összesen | 70,5% |
3. táblázat: Az egyes feladatok eredményessége az emelt szintű vizsgadolgozatokban (2024)
I. RÉSZ
Az idei emelt szintű feladatsor szokatlan eredményeket hozott. Az I. rész megoldottsága mindössze másodszor maradt 70% alatt a kutatás kezdete óta: az idei 68,5%-os eredmény a 2013-as 63% után a második legalacsonyabb. Ezzel szemben a II. rész megoldottsága rekordot döntött, elérve az eddigi legmagasabb értéket. Csak az elmúlt három évben fordult elő, hogy a II. rész megoldottsága 70% fölé emelkedett, és most először haladta meg az I. rész eredményét.
Az is csak másodszor fordult elő, hogy az I. rész mind a négy feladata 80% alatti megoldottságot mutatott: 2018-ban történt hasonló eset, bár akkor mind a négy feladat elérte a 74%-ot. Szintén másodszor fordul elő, hogy három feladat 70% alatti eredményt hozott (az első alkalom a 2013-as év volt), pedig általában az I. rész mind a négy feladata eléri a 70%-os megoldottságot.
Az első feladat sikerességét egyértelműen az inverzfüggvénnyel kapcsolatos c) kérdés húzta le, amelynek megoldottsága mindössze 48% lett, ami a feladatsorban a 9. c) részfeladattal együtt a leggyengébb eredményt hozta. Bár az inverzfüggvény fogalmával kapcsolatos kérdés szokatlan lehetett az 1. feladatban, a megoldáshoz mindössze az inverzfüggvény legalapvetőbb tulajdonságának ismerete volt szükséges. Az alacsony megoldottság azonban azt mutatja, hogy ez a fogalom még az emelt szinten vizsgázók körében is hiányosságként jelentkezik.
Kissé váratlanul a 2-3-4. feladatok mindegyike az I. részben megszokottnál nehezebbnek bizonyult, még az alfeladatok szintjén is: csak a 3. b) és a 4. b) kérdések megoldottsága haladta meg a 70%-ot, és mindhárom feladatban akadt egy olyan alfeladat, amelynek a megoldottsága a 60%-ot sem érte el.
II. RÉSZ
A II. rész 72%-os megoldottsága új rekordot jelent, 1%-kal felülmúlva a tavalyi, akkor szintén rekordot jelentő értéket. Érdekes módon az egyes feladatok megoldottsága és kihagyási aránya is nagyon hasonlóan alakult a tavalyihoz. Mind az öt feladat megoldottsága a 65 és 75 százalék közötti sávban mozgott, így idén sem voltak sem kiugróan nehéz, sem kiemelkedően könnyű feladatok.
Az idei második részben két olyan feladat volt, amely kiválóan mérte a vizsgázók képességeit. A feladat pontszáma és az összpontszám közötti korrelációs együttható az 5. és a 7. feladat esetében rendre 0,839 és 0,821 volt, amely értékek az elmúlt 13 év során feldolgozott 117 feladat közül a legjobb 10 között szerepelnek. Ha alfeladatonként vizsgáljuk a feladatok „magyarázó erejét” (azaz a fenti korrelációs együtthatót), kiemelkedően teljesített a 7. c) (adott alkotójú forgáskúpok közül a maximális térfogatú meghatározása), amelynek 0,777-es értéke a második legmagasabb a 2018 óta vizsgált 174 alfeladat között (csak a 2020/9. b) előzi meg). Érdekes módon a másik véglet éppen az idei feladatsorban a 7. b) feladat volt (0,207). Ennek a feladatnak nem elsősorban az volt a célja, hogy hatékonyan elkülönítse a jó és a gyengébb vizsgázókat, hanem inkább azt szolgálta, hogy előkészítse és felvezesse a 7. c) feladat problémáját.
A vizsgázók nagy része idén is jól felismerte, hogy a 9. feladat lehet a legnehezebb: ezt hagyták ki a legtöbben, bár a 33%-os kihagyási arány nem számít kiugróan magasnak. Emelt szinten is láthatók eltérések a különböző képességű vizsgázók választásaiban: a leggyengébbek (40% alatt teljesítők) körében a legkevésbé népszerű és egyben legnehezebbnek bizonyuló feladat az 5. volt. Ennek egyik valószínű oka, hogy a határérték-számítás és az integrálszámítás a követelmények között a legnehezebb témakörök közé tartoznak, és sokakat már önmagában a témakör is elriaszthatott a feladat megoldásától. A legjobbak (90% fölött teljesítők) több mint fele (51%) hagyta ki a 9. feladatot. Így a 9. feladatot kihagyók átlageredménye a teljes feladatsoron 68,2%, míg az 5. feladatot kihagyóké 73,3% volt.
Összefoglalva a fentieket elmondhatjuk, hogy a 2024-es közép- és emelt szintű feladatsor egyaránt megfelelt az új követelményeknek, fel lehetett ezekre készülni az előzetes információk alapján, az eredmények pedig azt mutatják, hogy ez a felkészülés sikeres volt.
Koncz Levente, Óbudai Árpád Gimnázium
Csapodi Csaba, ELTE