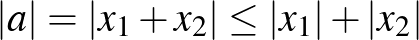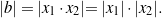A 2024 júniusában megjelent cikkben olyan 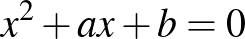 és
és  alakú másodfokú egyenletpárokat vizsgáltam, amelyeknél
alakú másodfokú egyenletpárokat vizsgáltam, amelyeknél  és
és 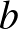 egész számok, és a két egyenlet gyökei szintén egész számok. Az alábbiakban vizsgált egyenletpárok megoldási módszere más matematikai eszközök bemutatását teszi lehetővé, tehát más szempontból érdekesek. Itt nem alkalmazunk komplex számokat a megoldások során, sokkal inkább támaszkodunk az emelt szintű érettségi követelményeire.
egész számok, és a két egyenlet gyökei szintén egész számok. Az alábbiakban vizsgált egyenletpárok megoldási módszere más matematikai eszközök bemutatását teszi lehetővé, tehát más szempontból érdekesek. Itt nem alkalmazunk komplex számokat a megoldások során, sokkal inkább támaszkodunk az emelt szintű érettségi követelményeire.
Középiskolai tanulmányok során gyakran találkozunk az 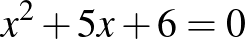 és az
és az 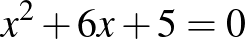 másodfokú egyenletekkel, amelyeknek a gyökei egyaránt egész számok. Másik ilyen „szerencsés” páros a következő két egyenlet:
másodfokú egyenletekkel, amelyeknek a gyökei egyaránt egész számok. Másik ilyen „szerencsés” páros a következő két egyenlet:  és
és 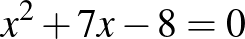 . Mindkét esetben a konstans tag és az elsőfokú tag együtthatóját felcserélve olyan másodfokú egyenletet kaptunk, amelynek szintén egész számok a gyökei, csakúgy, mint az eredetinek. ( Az alábbi ábrán a koordináta-rendszerben ábrázoltuk a fenti négy egyenlet megoldásait a függvények megrajzolásával.)
. Mindkét esetben a konstans tag és az elsőfokú tag együtthatóját felcserélve olyan másodfokú egyenletet kaptunk, amelynek szintén egész számok a gyökei, csakúgy, mint az eredetinek. ( Az alábbi ábrán a koordináta-rendszerben ábrázoltuk a fenti négy egyenlet megoldásait a függvények megrajzolásával.)
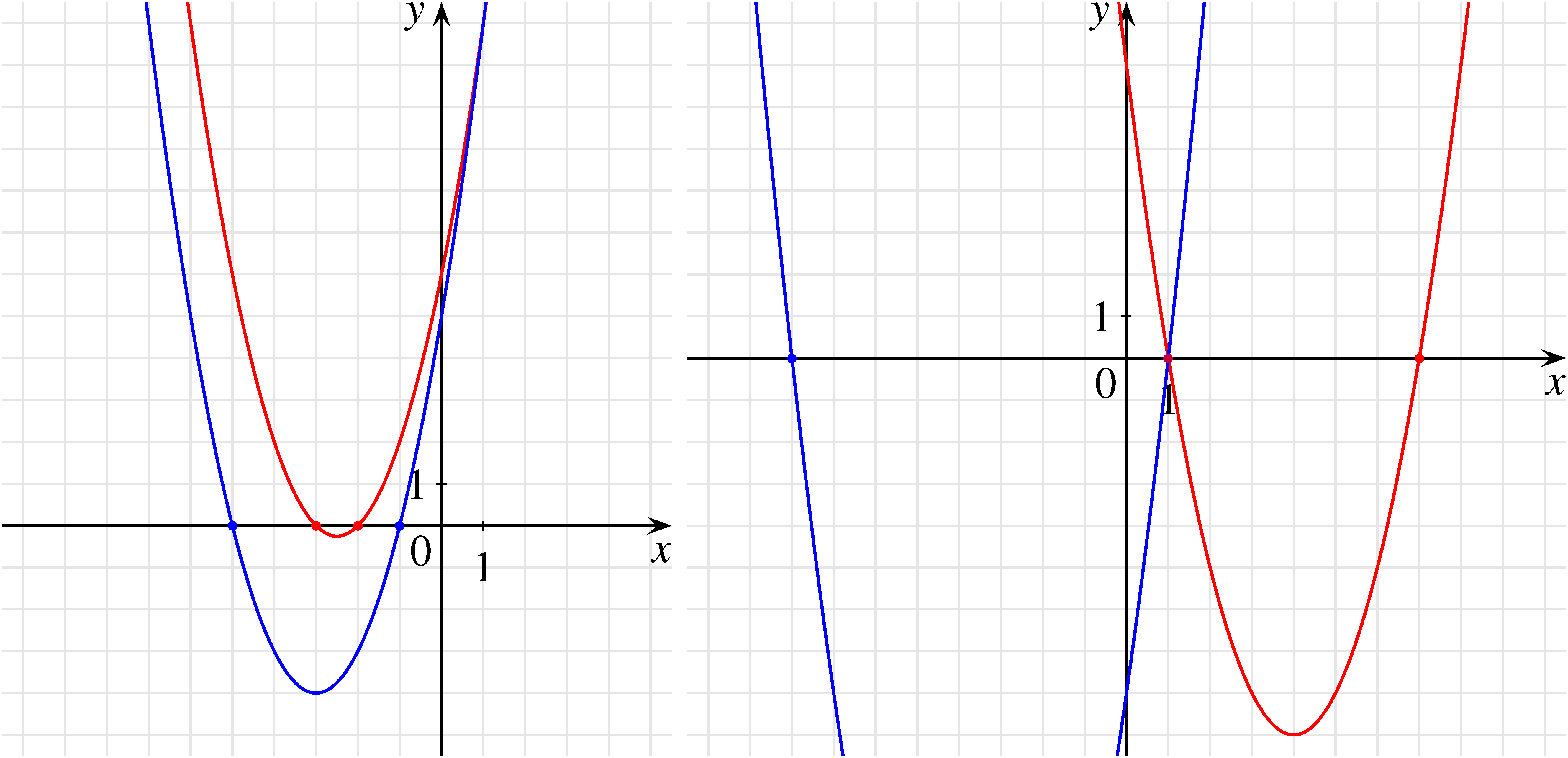
Ahogy azt a fent említett cikkben láttuk, ezúttal is felvethetjük matematika szakkörön és matematika tagozaton (vagy egyéb haladó csoportokban tanórán) az alábbi kérdéseket:
– Véges vagy végtelen sok ilyen páros létezik?
– Hogyan lehet ilyen egyenletpárokat előállítani a fenti két példán kívül (ha egyáltalán vannak)?
Ezekre a kérdésekre keressük a választ ebben a cikkben, és a probléma megoldásában a Viète-formulákat fogjuk segítségül hívni.
A probléma tehát a következő: melyek azok az  és
és 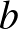 egész számok, amelyekre az
egész számok, amelyekre az 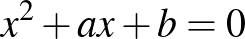 és az
és az 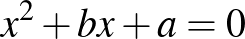 másodfokú egyenletek gyökei egyaránt egész számok?
másodfokú egyenletek gyökei egyaránt egész számok?
Elsőként vegyük észre, hogy ha 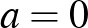 , akkor az
, akkor az 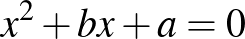 egyenlet gyökei 0 és
egyenlet gyökei 0 és 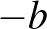 (ezek tehát egészek), az
(ezek tehát egészek), az 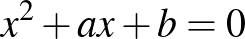 egyenlet gyökei viszont pontosan akkor lesznek egészek, ha
egyenlet gyökei viszont pontosan akkor lesznek egészek, ha 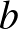 egy négyzetszám ellentettje. Hasonlóan, ha
egy négyzetszám ellentettje. Hasonlóan, ha 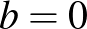 , akkor
, akkor  -nak egy négyzetszám ellentettjének kell lennie ahhoz, hogy egész gyököket kapjunk. Ezek a feladatunk triviális megoldásai, amelyekből végtelen sok van, és nem túl érdekesek a számunkra. Innentől kezdve a nemtriviális megoldásokat vizsgáljuk, vagyis feltesszük, hogy sem
-nak egy négyzetszám ellentettjének kell lennie ahhoz, hogy egész gyököket kapjunk. Ezek a feladatunk triviális megoldásai, amelyekből végtelen sok van, és nem túl érdekesek a számunkra. Innentől kezdve a nemtriviális megoldásokat vizsgáljuk, vagyis feltesszük, hogy sem  , sem
, sem 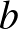 nem 0. Két esetet fogunk vizsgálni, ha
nem 0. Két esetet fogunk vizsgálni, ha 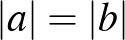 , illetve, ha
, illetve, ha 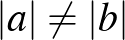 .
.
1. eset: 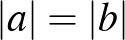 , és
, és 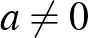 .
.
Ekkor két egyenletpárunk van, az egyik kétszer az 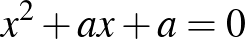 egyenletből, a másik pedig az
egyenletből, a másik pedig az 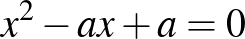 és az
és az 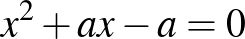 egyenletekből áll. Világos, hogy mindegyik egyenlet diszkriminánsának négyzetszámnak kell lennie. Az
egyenletekből áll. Világos, hogy mindegyik egyenlet diszkriminánsának négyzetszámnak kell lennie. Az 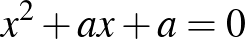 és az
és az 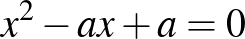 egyenlet diszkriminánsa közös, nevezetesen
egyenlet diszkriminánsa közös, nevezetesen 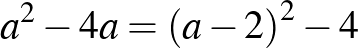 . Ezek szerint
. Ezek szerint 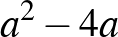 és
és 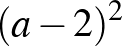 is négyzetszámok, és a különbségük 4. Nem nehéz ellenőrizni, hogy csak akkor lehet két négyzetszám különbsége 4, ha az egyik 0, a másik pedig 4. Azt kaptuk tehát ebből az észrevételből, hogy
is négyzetszámok, és a különbségük 4. Nem nehéz ellenőrizni, hogy csak akkor lehet két négyzetszám különbsége 4, ha az egyik 0, a másik pedig 4. Azt kaptuk tehát ebből az észrevételből, hogy  , amiből következik, hogy
, amiből következik, hogy 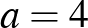 , hiszen
, hiszen 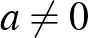 . Vagyis két egyenletpár jöhet szóba:
. Vagyis két egyenletpár jöhet szóba:
– az 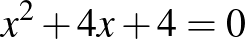 , amelyik saját magával alkot párt. Gyors számolással meggyőződhetünk róla, hogy ennek tényleg egész gyökei vannak:
, amelyik saját magával alkot párt. Gyors számolással meggyőződhetünk róla, hogy ennek tényleg egész gyökei vannak: 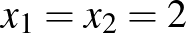 .
.
– a másik pedig az 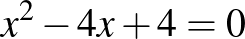 és
és  egyenletekből álló pár. Viszont a második egyenletnek nem egész számok a gyökei, azaz ebben az esetben az eredeti problémára nem kapunk megoldást.
egyenletekből álló pár. Viszont a második egyenletnek nem egész számok a gyökei, azaz ebben az esetben az eredeti problémára nem kapunk megoldást.
Az  esetben tehát egyetlen megoldás adódott:
esetben tehát egyetlen megoldás adódott: 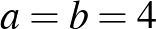 .
.
2. eset: 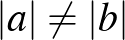 ,
, 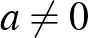 és
és 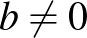 .
.
Mivel  és
és 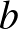 szerepe felcserélhető a kitűzött problémában, ezért feltehetjük, hogy
szerepe felcserélhető a kitűzött problémában, ezért feltehetjük, hogy 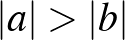 . Legyenek az
. Legyenek az 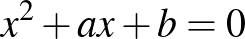 egyenlet gyökei
egyenlet gyökei 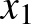 és
és 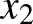 . Természetesen egyik sem lehet 0, mert
. Természetesen egyik sem lehet 0, mert 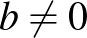 . A Viète-formulák alapján
. A Viète-formulák alapján 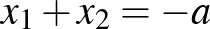 és
és 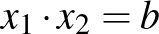 . Ebből, a háromszög-egyenlőtlenség általánosítását is felhasználva azt kapjuk, hogy:
. Ebből, a háromszög-egyenlőtlenség általánosítását is felhasználva azt kapjuk, hogy:
Mivel 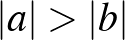 , ezért a következőt kapjuk:
, ezért a következőt kapjuk:
A gyökök abszolútértékei pozitív egész számok, és azt kaptuk, hogy a szorzatuk kisebb az összegüknél. Hogyan lehetséges ez? Legyenek 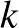 és
és 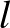 pozitív egészek, és tegyük fel, hogy
pozitív egészek, és tegyük fel, hogy

Az egyenlőtlenség mindkét oldalából kivonjuk a 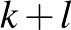 kifejezést és hozzáadunk 1-et.
kifejezést és hozzáadunk 1-et.
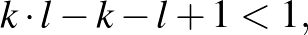
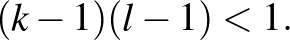
Mivel  és
és  nemnegatív egész számok, ez csak úgy lehetséges, ha legalább az egyikük 0, tehát
nemnegatív egész számok, ez csak úgy lehetséges, ha legalább az egyikük 0, tehát 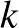 vagy
vagy 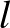 egyikének 1-nek kell lennie. Ezért (3) alapján valamelyik gyök abszolútértéke biztosan 1. Mivel
egyikének 1-nek kell lennie. Ezért (3) alapján valamelyik gyök abszolútértéke biztosan 1. Mivel 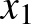 és
és 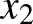 szerepe szimmetrikus, ezért feltehető, hogy
szerepe szimmetrikus, ezért feltehető, hogy 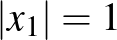 . Legyen
. Legyen 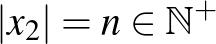 . Ekkor (2) miatt
. Ekkor (2) miatt 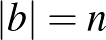 és (1) miatt
és (1) miatt 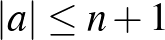 . Mivel
. Mivel 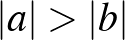 , ezért
, ezért 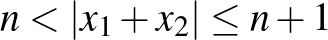 . Ebből pedig az következik, hogy
. Ebből pedig az következik, hogy 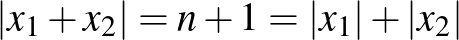 . Ha két, 0-tól különböző szám összegének abszolútértéke megegyezik az abszolútértékük összegével, akkor a két szám azonos előjelű. Tehát
. Ha két, 0-tól különböző szám összegének abszolútértéke megegyezik az abszolútértékük összegével, akkor a két szám azonos előjelű. Tehát 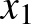 és
és 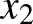 azonos előjelűek, ezért
azonos előjelűek, ezért 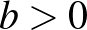 , tehát
, tehát 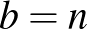 .
.
Innentől két esetet különböztetünk meg attól függően, hogy  pozitív vagy negatív.
pozitív vagy negatív.
a) 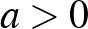 . Ekkor
. Ekkor 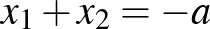 miatt a két gyök összege negatív, és mivel azonos előjelűek, ezért mindkettő negatív. Tehát
miatt a két gyök összege negatív, és mivel azonos előjelűek, ezért mindkettő negatív. Tehát  és
és 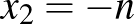 , így a Viète-formulák alapján
, így a Viète-formulák alapján  és
és 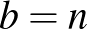 . Most tekintsük a kiindulási
. Most tekintsük a kiindulási 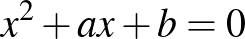 egyenlet párját, azaz az
egyenlet párját, azaz az 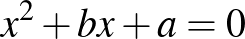 egyenletet. Ennek diszkriminánsa:
egyenletet. Ennek diszkriminánsa:
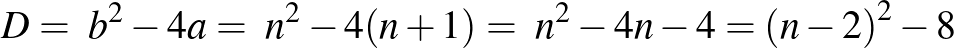 .
.Az egész gyökök miatt 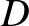 -nek négyzetszámnak kell lennie, és mivel
-nek négyzetszámnak kell lennie, és mivel 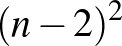 is négyzetszám, ezért két olyan négyzetszámot keresünk, amelyek különbsége 8. Nem nehéz ellenőrizni, hogy csak akkor lehet két négyzetszám különbsége 8, ha az egyik 1, a másik 9. Ezek szerint
is négyzetszám, ezért két olyan négyzetszámot keresünk, amelyek különbsége 8. Nem nehéz ellenőrizni, hogy csak akkor lehet két négyzetszám különbsége 8, ha az egyik 1, a másik 9. Ezek szerint 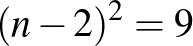 , amiből következik, hogy
, amiből következik, hogy 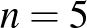 , mert
, mert 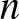 pozitív. Tehát
pozitív. Tehát 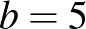 és
és 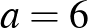 , vagyis ebben az esetben egyetlen megoldás adódott, a cikk elején is említett
, vagyis ebben az esetben egyetlen megoldás adódott, a cikk elején is említett 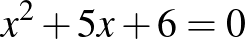 és az
és az 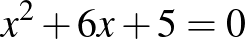 másodfokú egyenletpár.
másodfokú egyenletpár.
b) 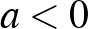 . Ekkor
. Ekkor 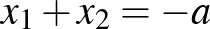 miatt mindkét gyök pozitív, ezért
miatt mindkét gyök pozitív, ezért 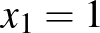 és
és 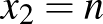 , valamint
, valamint 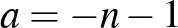 és
és 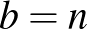 . Az
. Az 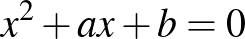 egyenlet párjának, vagyis az
egyenlet párjának, vagyis az 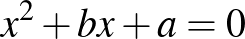 egyenletnek a diszkriminánsa:
egyenletnek a diszkriminánsa:

Az 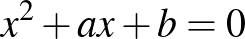 egyenlet diszkriminánsa pedig:
egyenlet diszkriminánsa pedig:
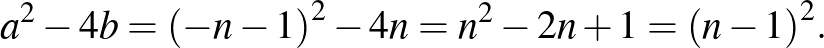
Látható, hogy mindkét egyenlet diszkriminánsa négyzetszám. Mivel a megoldóképletben szereplő számláló két tagjának paritása megegyezik, ezért ha 2-vel osztjuk, egész számokat kapunk, tehát egész számok lesznek a gyökei mindkét egyenletnek. Vagyis ebben az esetben végtelen sok, a feltételeknek megfelelő másodfokú egyenletpár létezik, hiszen 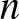 tetszőleges pozitív egész szám lehet.
tetszőleges pozitív egész szám lehet.
Összefoglalva: a cikkben kitűzött feladat nemtriviális megoldásai a következők:
– Az 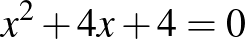 egyenlet, amelynek a párja önmaga.
egyenlet, amelynek a párja önmaga.
– Az 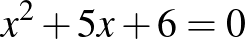 és az
és az 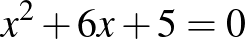 másodfokú egyenletpár.
másodfokú egyenletpár.
– Az 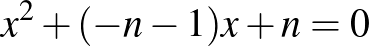 és az
és az 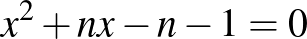 másodfokú egyenletpárok, ahol
másodfokú egyenletpárok, ahol 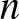 pozitív egész szám. Ebbe a kategóriába tartozik a cikk elején említett
pozitív egész szám. Ebbe a kategóriába tartozik a cikk elején említett  és
és 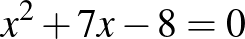 egyenletpár.
egyenletpár.
Beláttuk tehát, hogy végtelen sok nemtriviális megoldása van a cikkben kitűzött problémának, és egyúttal a Viète-formulákra is találtunk egy szép alkalmazást.