A matematikaoktatás jelenlegi helyzete a Révai Miklós Gimnáziumban
Korábbi cikkünkben bemutattuk a győri Révai Miklós Gimnázium kialakulásának történelmi vonatkozásait, valamint bemutattuk Arany Dániel, dr. Kárteszi Ferenc és Czapáry Endre munkásságát. Ebben az írásban az iskolában napjainkban zajló matematikaoktatást, a tehetséggondozás formáit és lehetőségeit tárgyaljuk.
A Révai Miklós Gimnáziumban nincs speciális matematika tagozat, de több osztálytípusban is kiemelten kezeljük a matematika oktatását.
Az „F osztály”
Az F osztály iskolánk jelenleg egyetlen hatévfolyamos képzést biztosító osztálya. Ebbe az osztályba hatodikos korukban válogatjuk ki a jelentkező kisdiákok közül a legjobbakat. A felvételi eljárásban a központi írásbeli vizsgák eredményén kívül figyelembe vesszük a szóbeli vizsgán elért teljesítményt is. A szóbeli vizsgán magyar nyelv, történelem és matematika tantárgyakból kérdezzük a jelentkezőket. A matematika-feladatlap három, a központi írásbeli feladatoknál kicsit nehezebb feladatot tartalmaz. A feladatlappal a matematikai szövegértés mellett a kombinatorikus gondolkodás, a modellalkotás és a geometriai alapismeretek alkalmazásának képességét mérjük. Az F osztályokban a matematika tanítása heti 4 tanórában csoportbontásban zajlik. A csoportok kialakítása kezdetben névsor szerint történik, de a matematika szempontjából ígéretesebb osztályokban a 8. vagy a 9. évfolyamon érdeklődés és képességek alapján kialakítunk egy „mini-fakultációs” csoportbontást egy erősebb és egy középszintet megcélzó csoport létrehozásával. Az F osztályba járó diákokkal tudunk a leghosszabb ideig foglalkozni, ezért a legkiválóbb versenyeredményeket legtöbbször az ebbe az osztályba járó diákok érik el.
Matematika–idegen nyelvi osztály
A C osztály négyévfolyamos képzése során a matematikát szintén kiemelten kezeljük. Ebben az osztálytípusban is csoportbontásban történik a matematika tanítása, heti 5 órában. Az osztály helyi tanterve alapján már az első két tanévben is emelt szintre készítjük fel a diákokat, de marad idő a versenyekre történő felkészítésre is.
Reál osztály
A D osztályunk jelenleg két eltérő érdeklődésű csoportból áll. Az osztály egyik fele biológia–kémia, a másik fele pedig matematika–fizika orientációt követ. A „mat–fizes” csoportban szintén heti 5 tanórában tanulják a diákok a matematikát, a C osztályokban alkalmazott tanterv alapján.
A fenti osztályokon kívül iskolánkban még egy négy évfolyamos osztályt (idegen nyelvi orientációval) és két öt évfolyamos képzést biztosító osztályt indítunk: egy nyelvi előkészítőt és egyet az Arany János Tehetséggondozó Program keretei közt.
A diákok az utolsó két tanévben fakultációt választhatnak. A matematika fakultációt választó tanulók egységesen heti 5 tanórában, az alapórát választók 3 tanórában tanulják a matematikát. Minden tanévben négy fakultációs csoportot indítunk: egyet-egyet a C, D, F osztályokban és egy „vegyes” csoportot a többi osztály tanulói számára.
Tehetséggondozás a Révaiban
Iskolánkban nagy múltra tekint vissza a matematika-tehetséggondozó munka, amelyről elmondhatjuk, hogy rendkívül sikeres, és amelyre nagyon büszkék vagyunk. A tehetséggondozás alapját a matematika szakkörök, tehetséggondozó foglalkozások adják, amelyekből minden tanévben összesen hatot indítunk, ami Győr–Moson–Sopron vármegyében különlegesen soknak számít. A szakköreinket évfolyami szinten szervezzük, heti 2-szer 45 perces foglalkozások formájában, és akár kis létszámmal is elindítjuk azokat.
A 7. évfolyam számára szervezett szakkörre iskolánk egyetlen 7. osztályából általában 3–10 tanuló szokott jelentkezni, ezért körülbelül 10 éve felmerült a munkaközösségünk tagjai közt, hogy a szakkört érdemes lenne kiterjeszteni városi szintre. Ez többé-kevésbé meg is valósult, azóta minden szakkörünk örömmel és szeretettel várja a város (és a környező települések) minden érdeklődő, tehetséges diákját. A 7. évfolyam számára indított szakkörünk nem titkolt célja a tehetséges diákok felfedezése és fejlesztése. Kezdetben logikai és egyéb egyszerű matematika eszköztárral megoldható feladatokkal foglalkozunk, majd később tematikus rendben dolgozzuk fel a versenyek feladatait. A 8. évfolyam számára szervezett szakkörökön a tematikus feldolgozás mellett egyre markánsabban jelennek meg nehezebb versenyfeladatok is.
Szakköri feladatok a 7. évfolyam számára
Összegek és szorzatok átalakításai
1. Melyek azok az egész számok, amelyekkel az 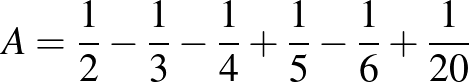 számot megszorozva egész számot kapunk eredményül?
számot megszorozva egész számot kapunk eredményül?
2. Mivel egyenlő a következő szorzat? Próbálj általánosítani!
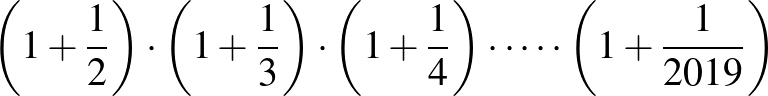
3. Mivel egyenlő a következő összeg? Próbálj általánosítani!
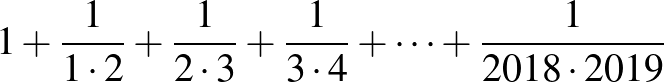
4. Keress olyan három egymást követő páros számot, amelyek szorzata 2-vel kezdődő és 2-re végződő hatjegyű szám? Vajon több ilyen számhármas is van? Miért?
5. Bergengóciában a távolbanézés nemzeti sportnak számít. Ebből a sportágból csapatversenyeket is szerveznek. A nemzeti ligában 2020 csapat versenyez, és bármely két csapat pontosan egy mérkőzést játszik egymással a szezon során. Összesen hány mérkőzésből áll a szezon?
6. Figyeld meg az alábbi szorzótáblát! Add össze a számokat a megjelölt „L” alakú sávokban! Fogalmazz meg sejtést az eredmények alapján! Vajon akkor is igaz a sejtés, ha a szorzótáblát tovább folytatjuk? Miért?
![\begin{picture}(5,5)\linethickness{7mm}
\put(0,1.5){\color{black!20}\line(1...
....5){\makebox(0,0)[c]{4}}%
\put(4.5,4.5){\makebox(0,0)[c]{5}}%
%
\end{picture}](/images/stories/latexuj/2024-11/2024-11-revai2/img5.png)
7. Helyezzetek el az ábrán látható 8 szobában

a) 18 b) 20 c) 25 d) 27 e) 30 f) 31 g) 32 h) 33
embert úgy, hogy mind a négy oldal mentén a 3-3 szobában lévő személyek száma pontosan 9 legyen!
8. Nyolc valós szám összege  , és közülük bármely hét összege pozitív. Mi az a legkisebb egész érték, amelyet nyolc ilyen szám valamelyike felvehet?
, és közülük bármely hét összege pozitív. Mi az a legkisebb egész érték, amelyet nyolc ilyen szám valamelyike felvehet?
A 9. és a 10. évfolyamos szakkörökre körülbelül 10 diákunk jár, és minden évben csatlakozik egy-két „külsős” diák is. A 11–12. évfolyam számára igazodva az OKTV-kiíráshoz, már csak egy szakkört indítunk.
Szakköri feladatok a 11–12. évfolyam számára
Vektorok skaláris szorzata
1. Bizonyítsuk be, hogy ha egy tetraéderben két kitérő élpár merőleges egymásra, akkor a harmadik élpár is merőleges egymásra!
2. Bizonyítsuk be, hogy egy tetraéder magasságvonalai akkor és csak akkor illeszkednek egy pontra, ha a tetraéder szemközti élei merőlegesek egymásra!
3. Az egy síkban fekvő 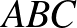 és
és 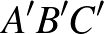 háromszögekről tudjuk, hogy az
háromszögekről tudjuk, hogy az 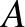 ,
, 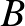 és
és  pontokból rendre a
pontokból rendre a 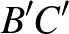 ,
, 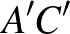 , illetve
, illetve 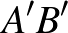 egyenesekre állított merőlegesek egy ponton haladnak át. Bizonyítsuk be, hogy az
egyenesekre állított merőlegesek egy ponton haladnak át. Bizonyítsuk be, hogy az 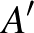 ,
, 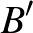 és
és 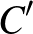 pontokból rendre a
pontokból rendre a 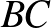 ,
, 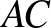 , illetve
, illetve 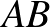 egyenesekre állított merőlegesek is egy ponton haladnak át!
egyenesekre állított merőlegesek is egy ponton haladnak át!
4. Bizonyítsuk be, hogy ha 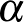 ,
, 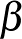 és
és 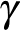 egy háromszög belső szögei, akkor
egy háromszög belső szögei, akkor
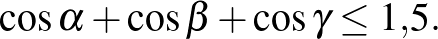
5. Bizonyítsuk be, hogy ha 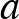 ,
, 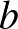 ,
, 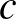 ,
, 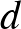 ,
, 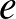 ,
, 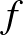 ,
, 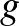 és
és 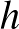 tetszőleges valós számok, akkor a következő összegek közül legalább az egyik nemnegatív:
tetszőleges valós számok, akkor a következő összegek közül legalább az egyik nemnegatív:

6. A tér közös kezdőpontból kiinduló 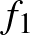 ,
, 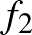 , …,
, …, 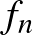 (
(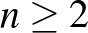 , egész) félegyenesei közül bármelyik kettő tompaszöget zár be egymással. Határozzuk meg
, egész) félegyenesei közül bármelyik kettő tompaszöget zár be egymással. Határozzuk meg 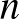 maximális értékét!
maximális értékét!
6. Oldjuk meg az alábbi egyenletet a valós számok halmazán!
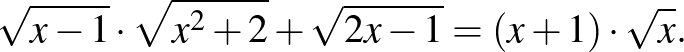
Az öt matematika szakkör mellett még egy további tehetséggondozó foglalkozást hirdetünk, elsősorban 12. évfolyamos diákok számára. Ez az Analízis szakkör, amely rendkívül népszerű a végzős diákok körében. A szakkör körülbelül 15 éve működik, és több funkciója van. Elsődleges célja a felkészítés az egyetemi tanulmányokra, a foglalkozások tematikája úgy került összeállításra, hogy lefedje a műszaki, gazdasági szakok első két féléves kalkulus tantárgyi követelményeinek jelentős részét. A szakkör közvetlen módon segíti a versenyekre és az emelt szintű érettségire felkészülést is, hiszen olyan technikákat is megismernek a diákok az analízis témaköreiből, amelyek jól használhatók a versenyeken vagy akár az érettségin is.
A tanórai keretek, a szakköri foglalkozások stabil alapot biztosítanak a motivált és tehetséges diákjaink számára, de messze nem elegendőt a sikeres versenyszereplésekhez. Elkötelezett és szakmailag felkészült matematikatanáraink a legkiválóbb diákjainkat egyénileg és sokoldalúan mentorálják. Ezekkel a diákokkal személyre szabottan igyekszünk foglalkozni, heti rendszerességgel szervezett egyéni (vagy szerencsés esetben kiscsoportos) felkészítő foglalkozásokkal, amelyeken gyakran szemezgetünk az OKTV, vagy nemzetközi matematikaversenyek feladataiból. Ehhez a munkához biztos hátteret ad tanáraink tapasztalata, egyénileg összeállított feladatbankjai, iskolánk jól felszerelt könyvtára. Az egyéni mentorálás során tanulóink figyelmét igyekszünk felhívni egyéb lehetőségekre is. Alázatos, szorgalmas és tehetséges diákjainkat bátorítjuk az Erdős Pál Matematikai Tehetséggondozó Iskola programjain való részvételre (veszprémi hétvégék, matematikatáborok), iskolánk alapítványán keresztül anyagi támogatásban is részesítjük őket. A legkiválóbb versenyzőinket támogatjuk a budapesti olimpiai szakkörön való részvételben is. A matematikai kutatómunka iránt érdeklődő diákjaink indulását segítjük tudományos cikkíró-pályázatokon (pl. Polygon pályázat középiskolásoknak). Összességében elmondható, hogy a Révai Miklós Gimnáziumban igyekszünk sokoldalú, személyre szabott felkészítő munkát végezni. Végezetül álljon itt iskolánk matematikai „dicsőségfala”, azaz legkiválóbb diákjaink elmúlt 15 évben elért eredményei:
Olimpikonjaink
| Név | Versenyeredmény |
| Mészáros András | IMO 2010: dicséret |
| Di Giovanni Márk | IMO 2014: ezüstérem |
| IMO 2015: bronzérem | |
| MEMO 2013: aranyérem | |
| Kocsis Anett1 | EGMO 2018: bronzérem |
| EGMO 2019: bronzérem | |
| EGMO 2020: bronzérem | |
| IMO 2020: bronzérem | |
| Jánosik Máté | MEMO 2021: bronzérem |
Arany Dániel Matematikai Tanulóverseny
| Név | Tanév | Helyezés |
| Vuchetich Bálint | 2008/2009 | dicséret |
| Nagy Gergely | 2011/2011 | dicséret |
| Di Giovanni Márk | 2012/2013 | 2. díj |
| Nagy Gergely | 2012/2013 | 2. díj |
| Nagy Fanni | 2012/2013 | dicséret |
| Póta Balázs | 2015/2016 | 2. díj |
| Jánosik Áron | 2016/2017 | 3. díj |
| Kocsis Anett | 2016/2017 | 3. díj |
| Póta Balázs | 2016/2017 | 1. díj |
| Balogh Zsófia | 2017/2018 | 1. díj |
| Jánosik Áron | 2017/2018 | 3. díj |
| Jánosik Máté | 2018/2019 | 1. díj |
| Balogh Zsófia | 2018/2019 | 1. díj |
| Jánosik Máté | 2019/2020 | 1. díj |
| Dékány Csaba | 2019/2020 | 2. díj |
| Hajba Milán | 2023/2024 | dicséret |
| Éliás Simon | 2023/2024 | 3. díj |
OKTV
| Név | Tanév | Helyezés |
| Gőgös Balázs | 2009/2010 | 1. |
| Mészáros András | 2009/2010 | 4. |
| Di Giovanni Márk | 2013/2014 | 1. |
| Nagy Gergely | 2013/2014 | 5. |
| Di Giovanni Márk | 2014/2015 | 1. |
| Póta Balázs | 2017/2018 | 5. |
| Jánosik Áron | 2018/2019 | 3. |
| Póta Balázs | 2018/2019 | 5. |
| Jánosik Áron | 2019/2020 | 1. |
| Jánosik Máté | 2020/2021 | 1. |
| Dékány Csaba | 2020/2021 | 5. |
| Jánosik Máté | 2021/2022 | 1. |
Lábjegyzet
- 1 Kocsis Anett a Fazekas Mihály Gimnáziumban érettségizett.











