A cikk első része a IV. fejezettel folytatódik: most a kockadobások, a geometria és a matematikai játékok világába kalauzoljuk el a kedves Olvasót. Azt szokták mondani, hogy aki a játékokat szereti, az szellemiségében örökké fiatal marad, és biztosan szereti a matematikát is. Reméljük, hogy a közölt feladatok ezt igazolni fogják. A geometriai feladatokkal pedig azt próbáljuk illusztrálni, hogy egy váratlan gondolat vagy egy megfelelően irányított döntéssorozat hogyan segítheti elő nehéz problémák megoldását. A közölt példákkal a geometria sokszínűségét is szeretnénk megmutatni.
IV. Játék nem szabályos dobókockákkal
9. feladat. Rózinak van két azonos „nem szabályos” dobókockája (azaz nem teljesül rá, hogy az egyes kimenetelek valószínűsége ugyanannyi), amelynek lapjain az 1, 2, 3, 4, 5, 6 számok szerepelnek. Rózi elgurítja a két kockát, és képezi a dobott számok összegét. A 2-es összeg valószínűsége 0,04, a 12-é 0,01.
Mennyi lehet a 7-es összeg maximális esélye?
Megoldás.
Legyen 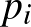 az
az  szám dobásának esélye (
szám dobásának esélye (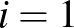 , 2, …, 6). Ekkor
, 2, …, 6). Ekkor  és
és 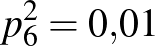 , amiből
, amiből 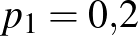 és
és 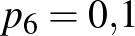 . Ebből
. Ebből 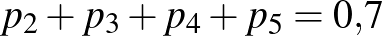 .
.
A korábbi feltételek teljesülése esetén a
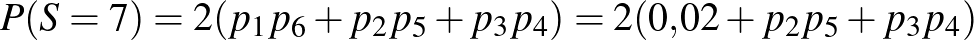
kifejezés maximumát keressük.
Vezessük be a 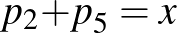 és
és 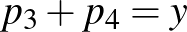 jelöléseket. A számtani és mértani közép közötti összefüggést felhasználva:
jelöléseket. A számtani és mértani közép közötti összefüggést felhasználva:
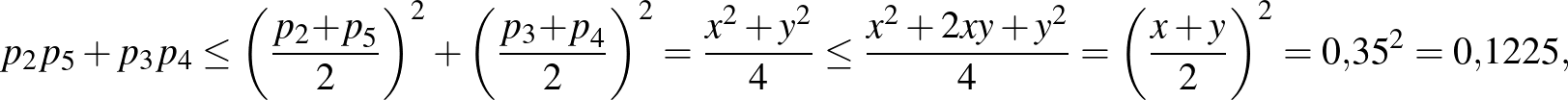
és így
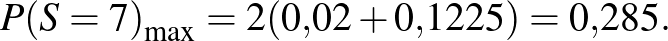
Az egyenlőség feltétele:  ,
, 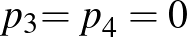 vagy
vagy 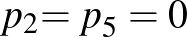 ,
, 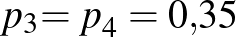 .
.
10. feladat. Lehetséges-e két kockát úgy „cinkelni” (tehát az egyes számok dobásának valószínűségét a kockán úgy megváltoztatni), hogy a két kockával dobva 2-től 12-ig minden összegnek ugyanakkora legyen a valószínűsége?
Megoldás. Jelölje 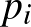 és
és 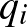 az
az  szám dobásának esélyét a két kockán (
szám dobásának esélyét a két kockán (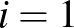 , 2, …, 6). Ekkor megfelelő „cinkelés” esetén – mivel 11 különböző kimenetel lehet –, a feltétel szerint mindegyiknek 1/11 valószínűségűnek kell lennie. Így
, 2, …, 6). Ekkor megfelelő „cinkelés” esetén – mivel 11 különböző kimenetel lehet –, a feltétel szerint mindegyiknek 1/11 valószínűségűnek kell lennie. Így
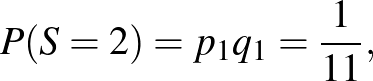


A 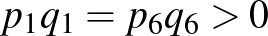 feltétel alapján a
feltétel alapján a 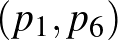 ,
, 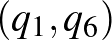 valószínűség-párok nagyságviszonya ellentétes. Ennek figyelembevételével:
valószínűség-párok nagyságviszonya ellentétes. Ennek figyelembevételével:


Így 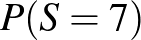 nem lehet 1/11.
nem lehet 1/11.
Tehát a kockákat nem lehet úgy „cinkelni”, hogy teljesítsék a feladat feltételét.
11. feladat. Egy gyárban Andris és Dávid kockákat készít. Mindkét fiú elkészíti saját kockáját is. Andris a szokásoknak megfelelően 1, 2, 3, 4, 5, 6 pontot helyez el a kockája lapjaira. A rafinált Dávid szintén 21 pontot oszt el a kockáján, de nem a szokásoknak megfelelően, hanem az egyes lapokra egyedi elrendezésben tesz nemnegatív számú pontokat. (Az ismétlődés is megengedett.) Ezután a két fiú elkezd játszani.
Az nyer, aki nagyobb számot dob. Egyenlő pontérték esetén addig dobálnak, amíg a csata el nem dől.
Mekkora a maximális valószínűsége annak, hogy Dávid nyer?
Adjunk példát olyan kockapontozásra, amellyel ez az esély elérhető.
Megoldás. Jelölje 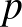 Dávid nyerési esélyét,
Dávid nyerési esélyét, 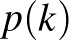 pedig annak a valószínűségét, hogy Dávid elsőre
pedig annak a valószínűségét, hogy Dávid elsőre 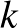 értéket dobva le tudja győzni Andrist. Felhasználva, hogy döntetlen helyzet után Dávid
értéket dobva le tudja győzni Andrist. Felhasználva, hogy döntetlen helyzet után Dávid 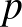 eséllyel nyer a játék folytatása során,
eséllyel nyer a játék folytatása során,

A 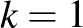 , 2, 3, 4, 5, 6 értékekre vonatkozó képletet annak alapján kapjuk, hogy Andris kockáján
, 2, 3, 4, 5, 6 értékekre vonatkozó képletet annak alapján kapjuk, hogy Andris kockáján 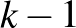 db
db 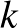 -nál kisebb pontérték található, és
-nál kisebb pontérték található, és  esély van az első dobás utáni döntetlen helyzetre.
esély van az első dobás utáni döntetlen helyzetre.
Jelöljük Dávid kockáján a pontértékeket 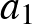 ,
, 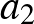 , …,
, …, 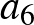 -tal. Ekkor
-tal. Ekkor
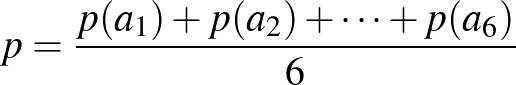
Tegyük fel, hogy Dávid kockáján pontosan  db lapon van pozitív pontérték.
db lapon van pozitív pontérték.
Ha  , akkor Dávid kockáján a lapoknak legalább a fele automatikusan vesztő, így nyerési esélye
, akkor Dávid kockáján a lapoknak legalább a fele automatikusan vesztő, így nyerési esélye 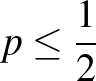 .
.
 esetén tegyük fel, hogy a Dávid kockáján szereplő pozitív pontértékek
esetén tegyük fel, hogy a Dávid kockáján szereplő pozitív pontértékek 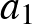 ,
, 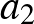 , …,
, …, 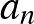 , és vegyük figyelembe, hogy
, és vegyük figyelembe, hogy  (
(  ).
).
Emiatt

A kapott egyenlőtlenségből a 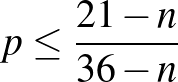 feltétel adódik.
feltétel adódik.
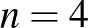 , 5, 6 esetén kiszámítva
, 5, 6 esetén kiszámítva 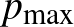 -ot, az alábbi értékeket kapjuk:
-ot, az alábbi értékeket kapjuk:
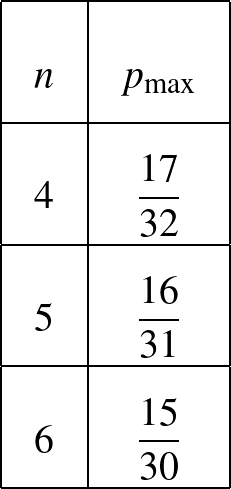
Tehát Dávid maximális nyerési esélye 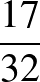 , és ez az esély akkor érhető el, ha a kockáján 4 lapra helyez el összesen 21 pontot, és pontosan két lapot hagy üresen. Vagyis 6, 6, 6, 3, 0, 0 vagy 6, 6, 5, 4, 0, 0 vagy 6, 5, 5, 5, 0, 0 pontot tesz a kocka lapjaira (tetszőleges elrendezésben).
, és ez az esély akkor érhető el, ha a kockáján 4 lapra helyez el összesen 21 pontot, és pontosan két lapot hagy üresen. Vagyis 6, 6, 6, 3, 0, 0 vagy 6, 6, 5, 4, 0, 0 vagy 6, 5, 5, 5, 0, 0 pontot tesz a kocka lapjaira (tetszőleges elrendezésben).
V. Valószínűség a geometria területén
12. feladat. Egy 1 m hosszúságú pálcát 7 töréssel 8 részre osztunk fel. Minden lépésben véletlenszerűen, azaz egyenlő eséllyel kiválasztunk egy rendelkezésre álló pálcadarabot, és azt pontosan középen kettétörjük.
Mennyi a valószínűsége annak, hogy a végén minden darab hossza  m lesz?
m lesz?
Megoldás.
Az első törés 1-féleképpen,
a második törés 2-féleképpen,
a hetedik törés 7-féleképpen történhet, ezért a pálca feldarabolására összesen 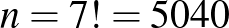 lehetőség adódik.
lehetőség adódik.
A megfelelő darabolás esetén az első törés egyértelmű.
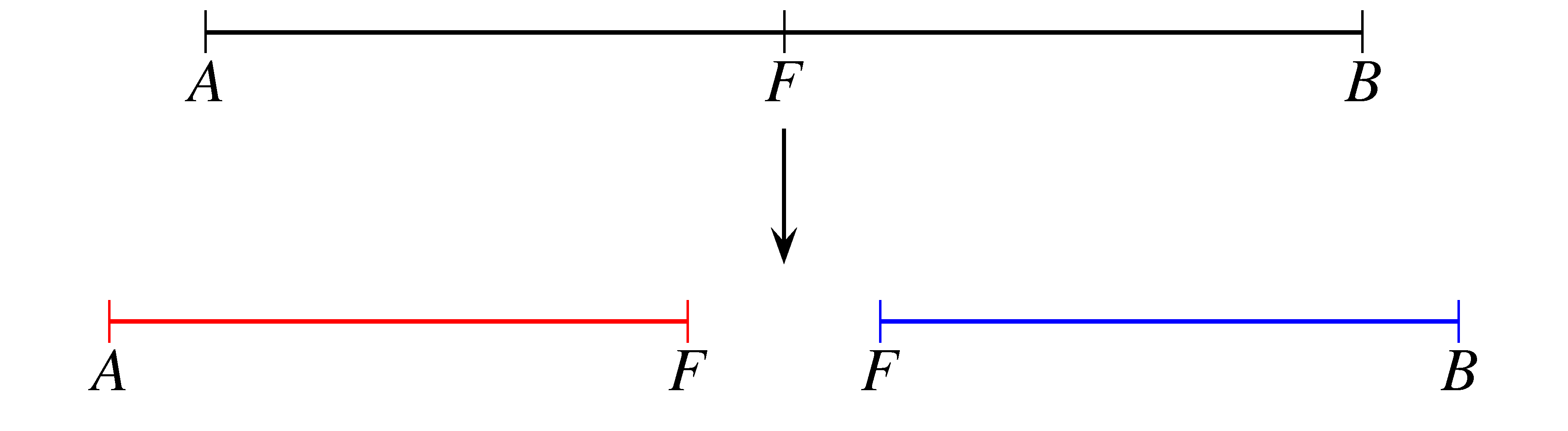
Ezután 3 törést az 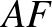 , 3 törést az
, 3 törést az 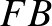 szakaszon kell végrehajtani. A törések sorrendje
szakaszon kell végrehajtani. A törések sorrendje 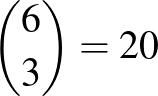 -féleképpen valósítható meg.
-féleképpen valósítható meg.
A megállapított sorrend ismeretében az 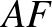 és
és 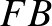 részek felezése már egyértelműen végezhető el.
részek felezése már egyértelműen végezhető el.
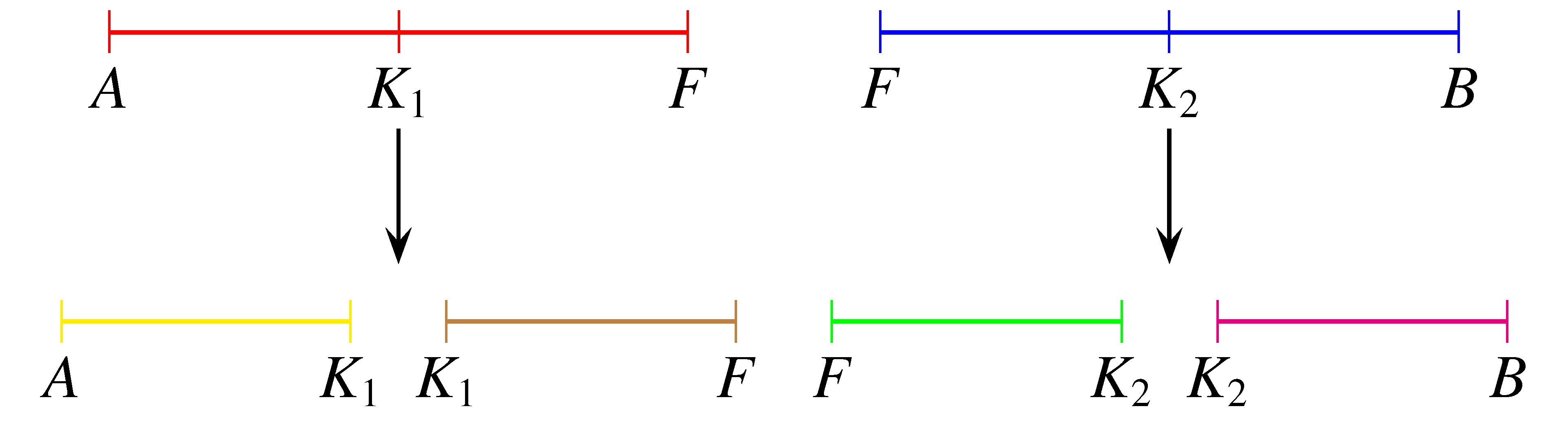
Az  és
és  darabok törése után az (
darabok törése után az ( ,
, 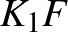 ) és (
) és (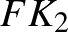 ,
, 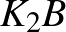 ) párokon belül a törési sorrend 2–2-féle lehet, így a kedvező esetek száma:
) párokon belül a törési sorrend 2–2-féle lehet, így a kedvező esetek száma:
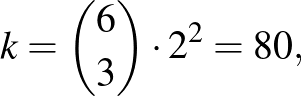
a keresett valószínűség pedig
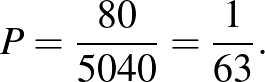
13. feladat. A 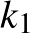 és
és 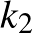 koncentrikus körök sugarainak hossza rendre 1, illetve 2 egység. A
koncentrikus körök sugarainak hossza rendre 1, illetve 2 egység. A 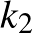 körvonalon véletlenszerűen kiválasztunk 4 különböző pontot, és összekötjük azokat úgy, hogy egy konvex négyszöget alkossanak.
körvonalon véletlenszerűen kiválasztunk 4 különböző pontot, és összekötjük azokat úgy, hogy egy konvex négyszöget alkossanak.
Mennyi a valószínűsége annak, hogy a négyszög oldalainak van közös pontja 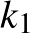 -gyel?
-gyel?
Megoldás.
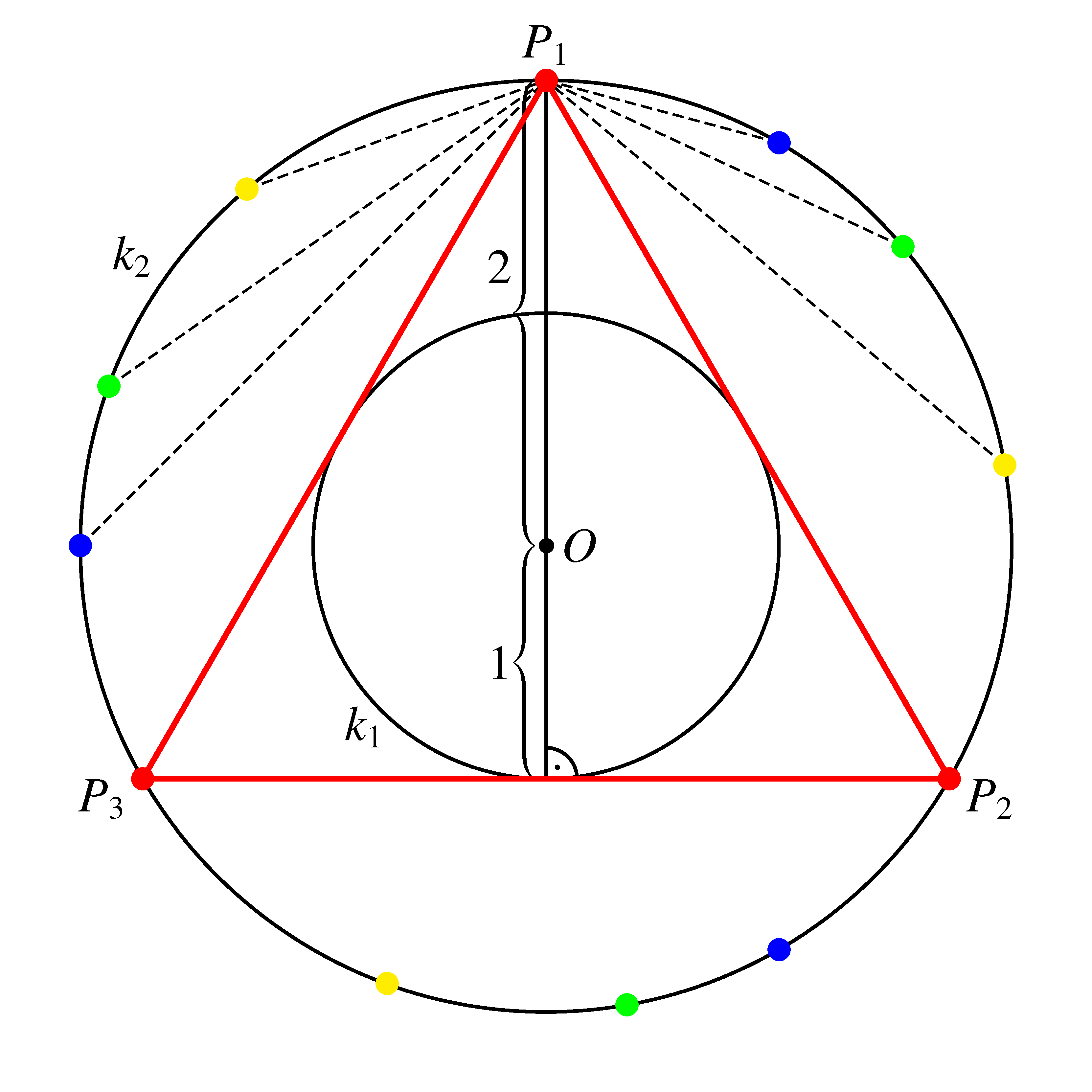
Nevezzünk triónak 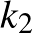 -n egy olyan ponthármast, amely pontjai szabályos háromszöget alkotnak. Egy ilyen trió által meghatározott háromszög oldalai érintik
-n egy olyan ponthármast, amely pontjai szabályos háromszöget alkotnak. Egy ilyen trió által meghatározott háromszög oldalai érintik 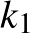 -et.
-et.
Ahelyett, hogy 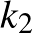 -n véletlenszerűen jelölnénk ki 4 különböző pontot, válasszunk véletlenszerűen 4 közös pont nélküli triót, majd ezekből véletlenszerűen jelöljünk ki 1-1 pontot. Így megvalósul a feladat szerinti pontok kiválasztása
-n véletlenszerűen jelölnénk ki 4 különböző pontot, válasszunk véletlenszerűen 4 közös pont nélküli triót, majd ezekből véletlenszerűen jelöljünk ki 1-1 pontot. Így megvalósul a feladat szerinti pontok kiválasztása 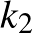 -n.
-n.
Vizsgáljuk meg, hogy a 4 pont által meghatározott konvex négyszögnek milyen valószínűséggel nem lesz közös pontja 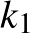 -gyel. Ennek szükséges és elégséges feltétele, hogy a négyszög csúcsai első-, másod- vagy harmadszomszédos pontok legyenek
-gyel. Ennek szükséges és elégséges feltétele, hogy a négyszög csúcsai első-, másod- vagy harmadszomszédos pontok legyenek 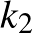 -n. Ennek figyelembevételével az alábbi két lehetőség kínálkozik arra, hogy a konvex négyszög oldalainak ne legyen közös pontja
-n. Ennek figyelembevételével az alábbi két lehetőség kínálkozik arra, hogy a konvex négyszög oldalainak ne legyen közös pontja 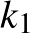 -gyel.
-gyel.
a) 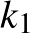 a négyszög belsejében található.
a négyszög belsejében található.
Ekkor minden megfelelő négyszög csúcsai között csak harmadszomszédos pontok lehetnek  -n. Három ilyen négyszög létezik:
-n. Három ilyen négyszög létezik: 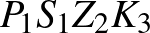 ,
, 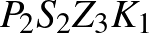 ,
, 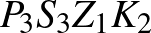 .
.
b)  a négyszögön kívül található.
a négyszögön kívül található.
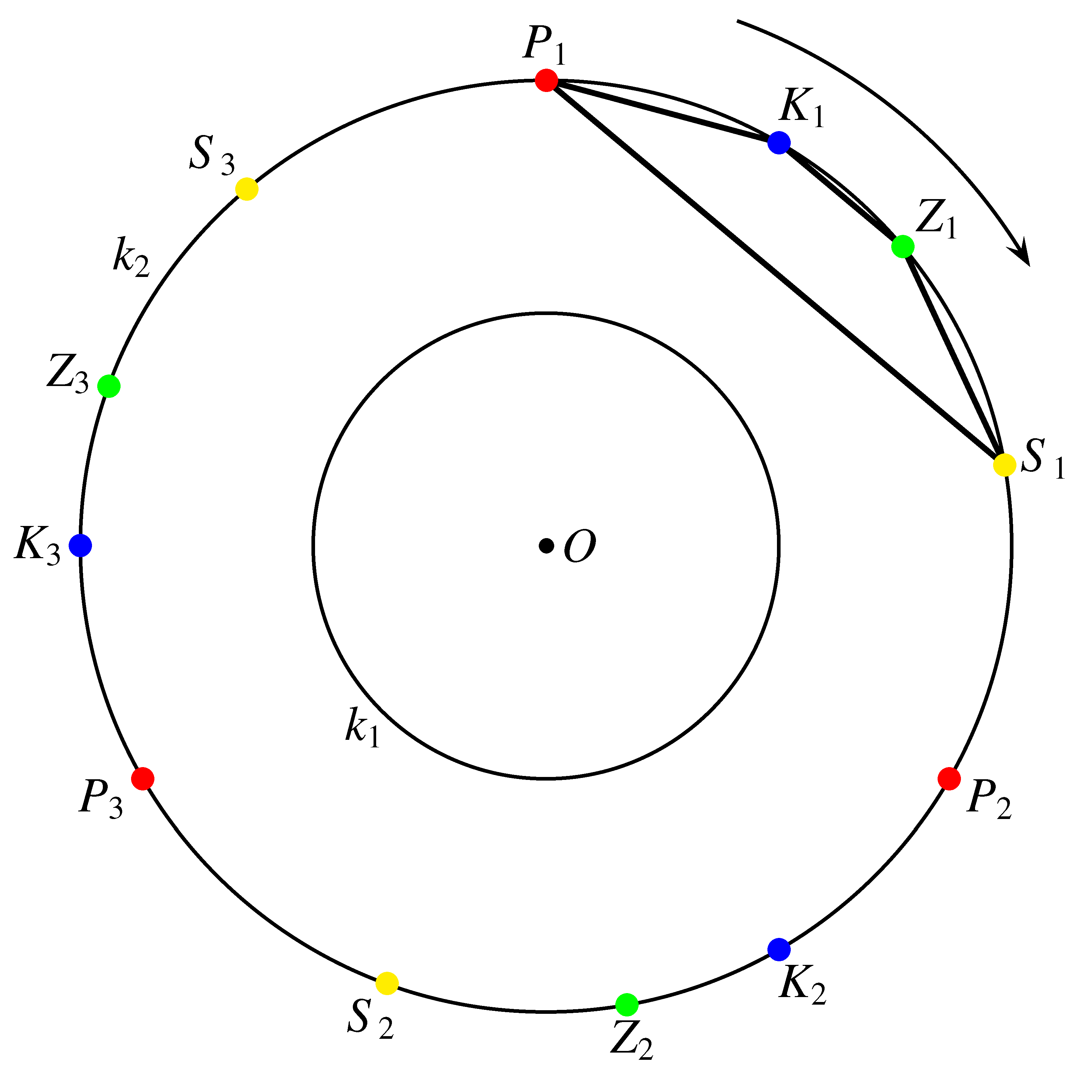
Ekkor a 4 kiválasztott pont közül a két legtávolabbi harmadszomszédos csúcs.
12 ilyen négyszög létezik. Így a 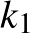 -gyel diszjunkt négyszögek száma összesen 15.
-gyel diszjunkt négyszögek száma összesen 15.
Mivel a triókon belül a négyszög csúcsainak kiválasztása 3-3-féleképpen történhet, ezért az összes esetek száma  , és az általunk vizsgált valószínűség:
, és az általunk vizsgált valószínűség:
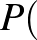 négyszög
négyszög 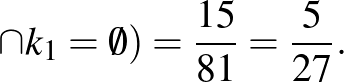
Ennek figyelembevételével annak esélye, hogy a négyszög oldalainak van közös pontja  -gyel:
-gyel:
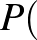 négyszög
négyszög 
Megjegyzés. A feladat általánosítható.
Ha 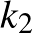 -n
-n 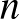 -szöget (
-szöget (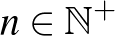 ,
, 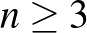 ) jelölünk ki, akkor annak a valószínűsége, hogy a sokszög oldalainak van
) jelölünk ki, akkor annak a valószínűsége, hogy a sokszög oldalainak van 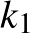 -gyel közös pontja:
-gyel közös pontja: 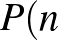 -szög
-szög 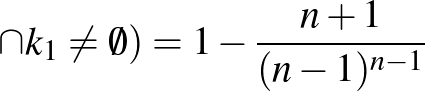 (
(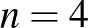 esetén
esetén 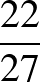 ).
).
VI. Győzelmi esély optimális játékstratégia esetén
14. feladat. Egy játékbemutatón Vikinek egy 2024 darabból álló golyósorozatot mutatnak meg egyesével. A golyók mindegyike piros vagy kék. Viki minden lépésben csak egy golyót lát, és azzal az alábbi három dolgot teheti:
 ha az piros, és megtartja, akkor
ha az piros, és megtartja, akkor 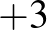 pontot kap,
pontot kap,
 ha az kék, és megtartja, akkor
ha az kék, és megtartja, akkor 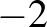 pontot kap,
pontot kap,
 ha a golyót nem kéri, akkor 0 pontot kap.
ha a golyót nem kéri, akkor 0 pontot kap.
A döntését később már nem változtathatja meg. A színeloszlás véletlenszerű. Viki akkor nyer, ha pontszámai összege éppen 1.
Mennyi az esélye annak, hogy nyer, ha ügyesen játszik?
Megoldás.
a)

Ha a sorozatban minden golyó piros, akkor Viki csak 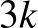 (
( 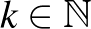 ,
, 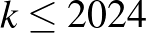 ) pontot szerezhet, és nem nyerhet.
) pontot szerezhet, és nem nyerhet.
b)

Ha a sorozatban minden golyó kék, akkor Viki csak 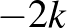 (
( 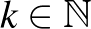 ,
, 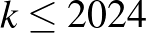 ) pontot szerezhet, és nem nyerhet.
) pontot szerezhet, és nem nyerhet.
c)

Ha a sorozatban mindkét színű golyó előfordul, akkor Viki biztosan nyerhet, ha az első piros és az első kék golyót megtartja, a többit nem kéri. Mivel a 2024 tagú sorozatban minden golyó színe 2-féle lehet, ezért Viki nyerési esélye:
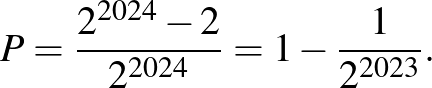
15. feladat.
Egy asztalon 3 megkülönböztethetetlen doboz áll. Az egyikben 2 piros, a másikban 2 kék, a harmadikban 1-1 piros és kék golyó van. A dobozok sorrendje véletlenszerű. Dia két golyót fog kivenni valahonnan; akár különböző, akár ugyababból a dobozból. Előtte azonban „megjósolja”, hogy azok színe azonos vagy különböző lesz-e. Ezután kivesz egy golyót az egyik dobozból, és megnézi. A 2. golyót bármelyik dobozból kihúzhatja. Akkor nyer, ha az eredeti tippje bejön.
Mit mondjon, majd milyen stratégiával húzzon (vagyis az első húzás után váltson-e dobozt, vagy sem) ahhoz, hogy maximális esélye legyen a nyerésre? Mennyi esélye van a győzelemre?
Megoldás. Jelöljük az egyes dobozokat az ábra szerint  ,
,  ,
,  -vel, és ugyanígy azokat az eseményeket is, amikor Dia ezekből húz golyót.
-vel, és ugyanígy azokat az eseményeket is, amikor Dia ezekből húz golyót.
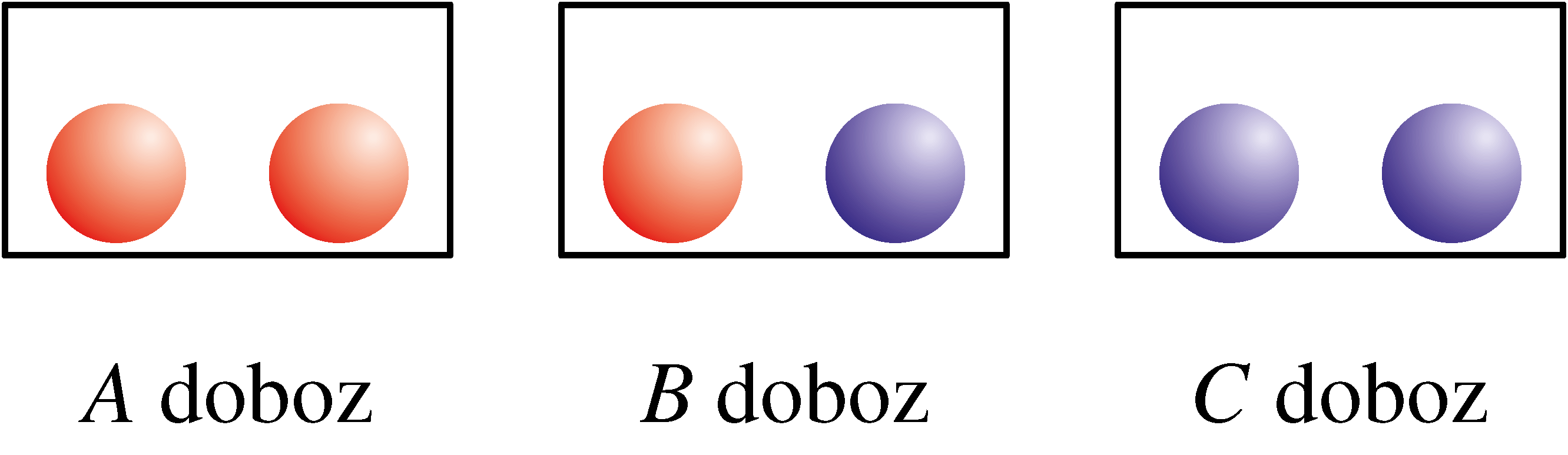
Az általánosság megszorítása nélkül feltehetjük, hogy Dia első kihúzott golyója piros. Ekkor
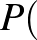 piros
piros 
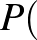 piros
piros 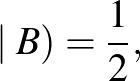
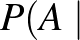 piros
piros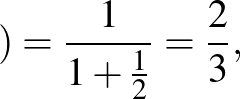
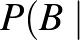 piros
piros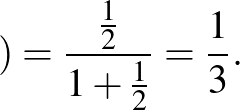
Vizsgáljuk ezután Dia nyerési esélyét aszerint, hogy mi volt az eredeti tippje, illetve a két húzását melyik dobozból végzi el.
I. eset: Dia eredeti jóslata két azonos színű golyó.
a) Ha Dia nem vált dobozt:
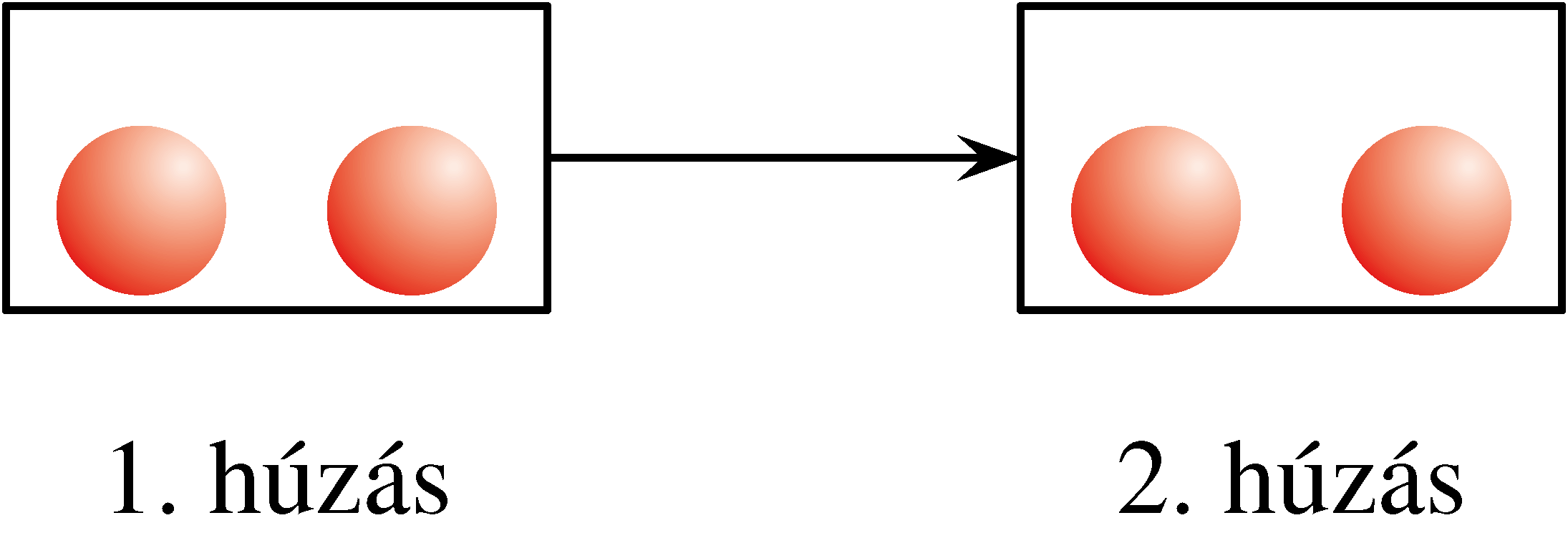
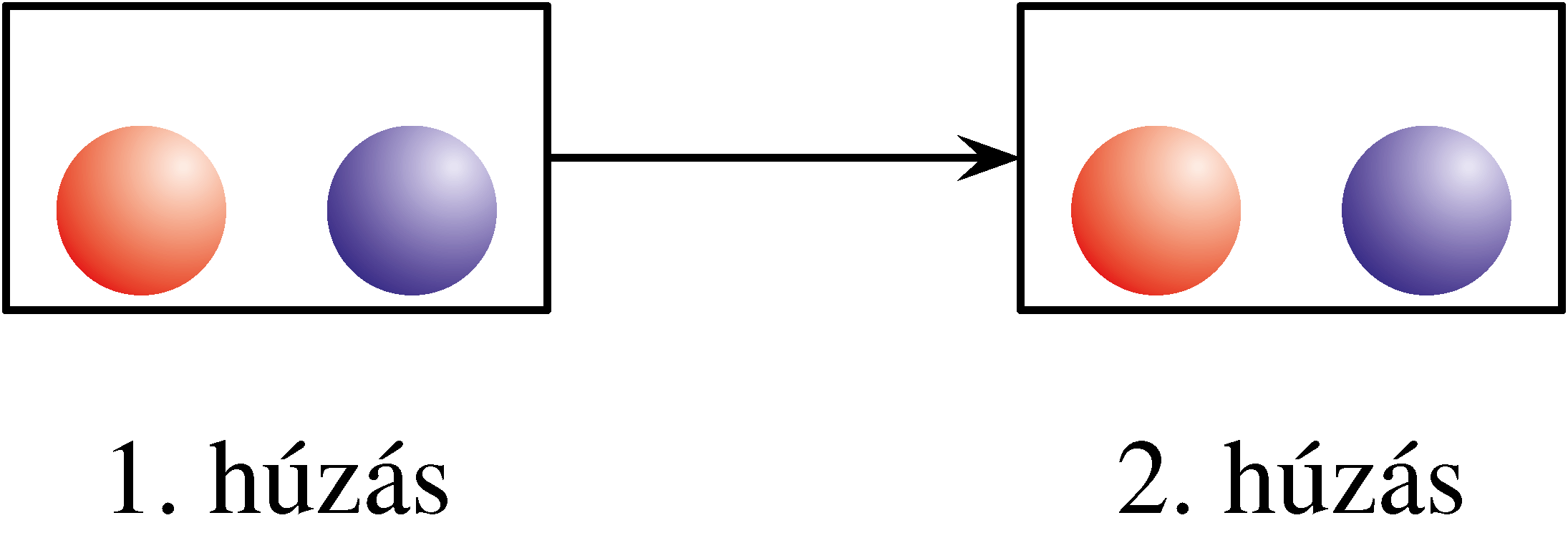
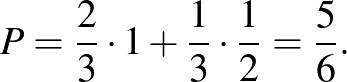
b) Ha Dia dobozt vált:

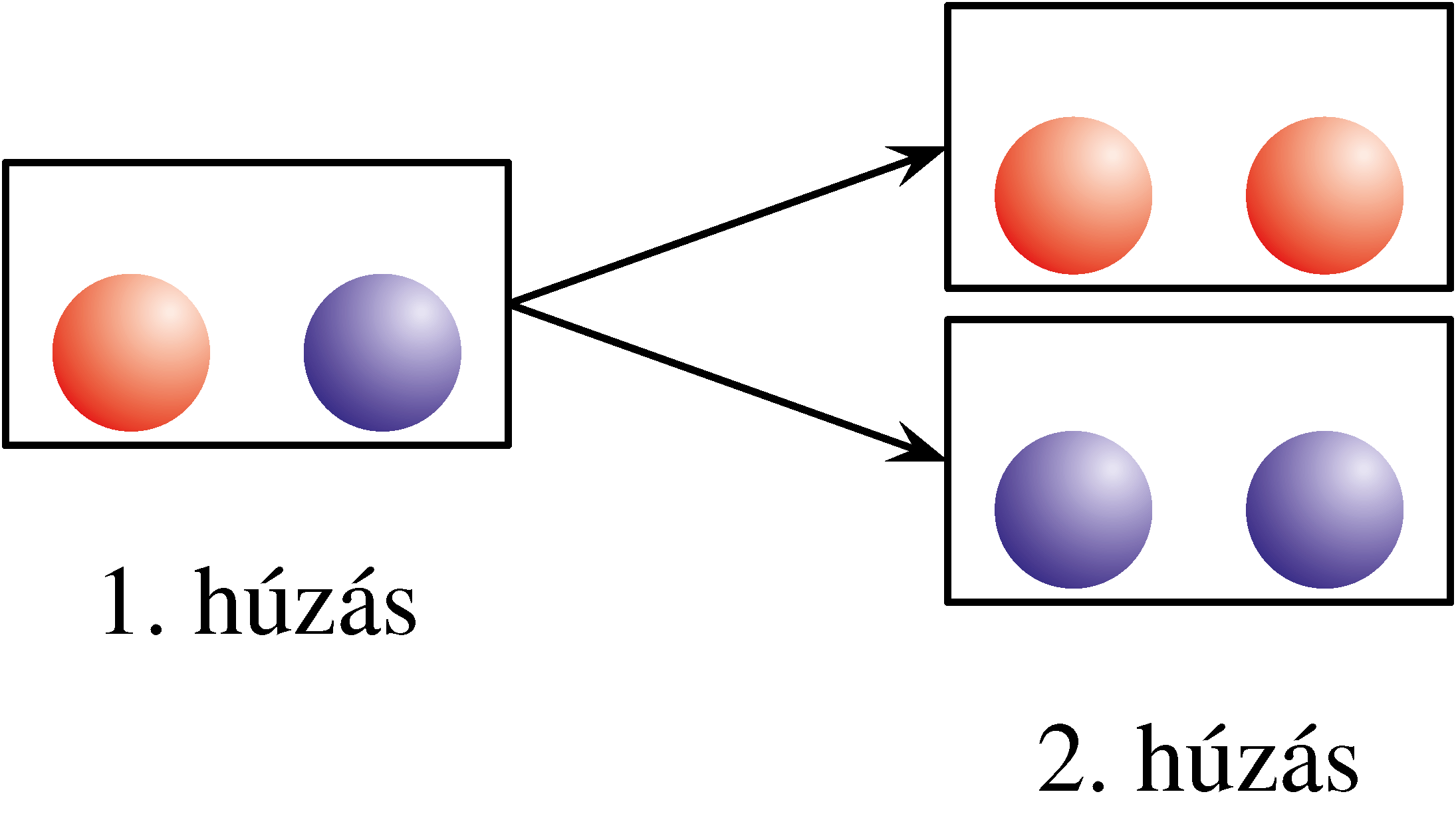
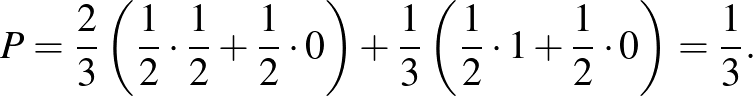
II. eset: Dia eredeti jóslata két különböző színű golyó.
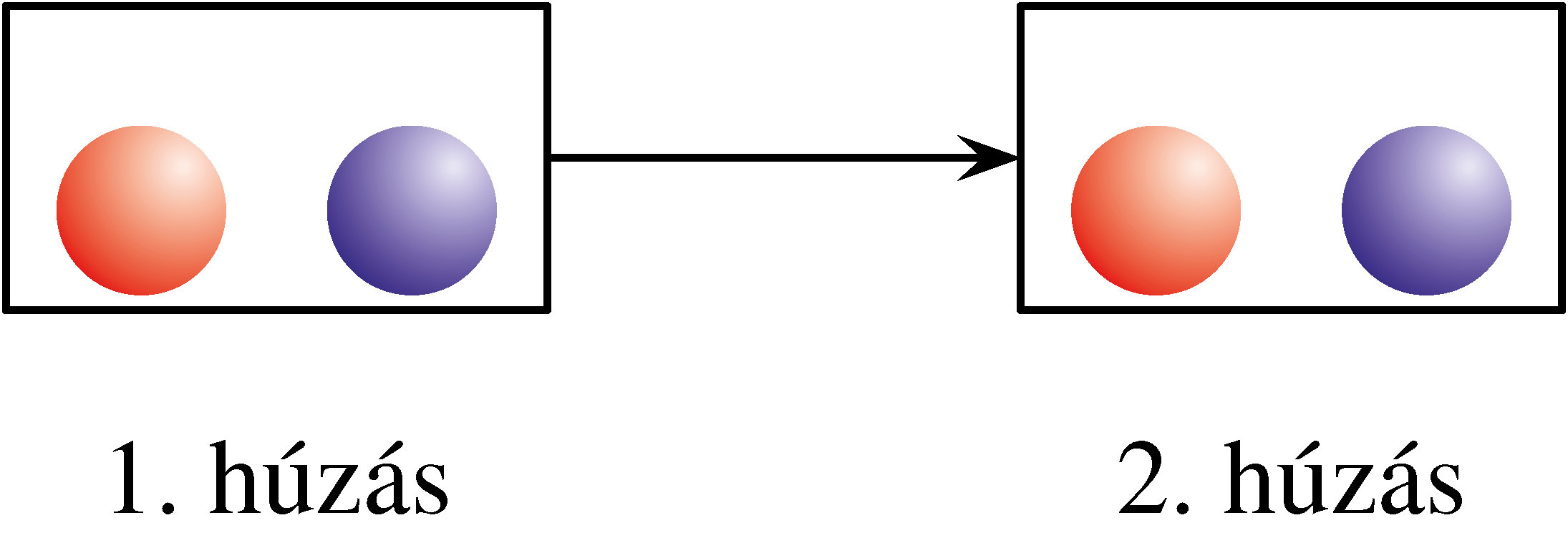
c) Ha Dia nem vált dobozt:


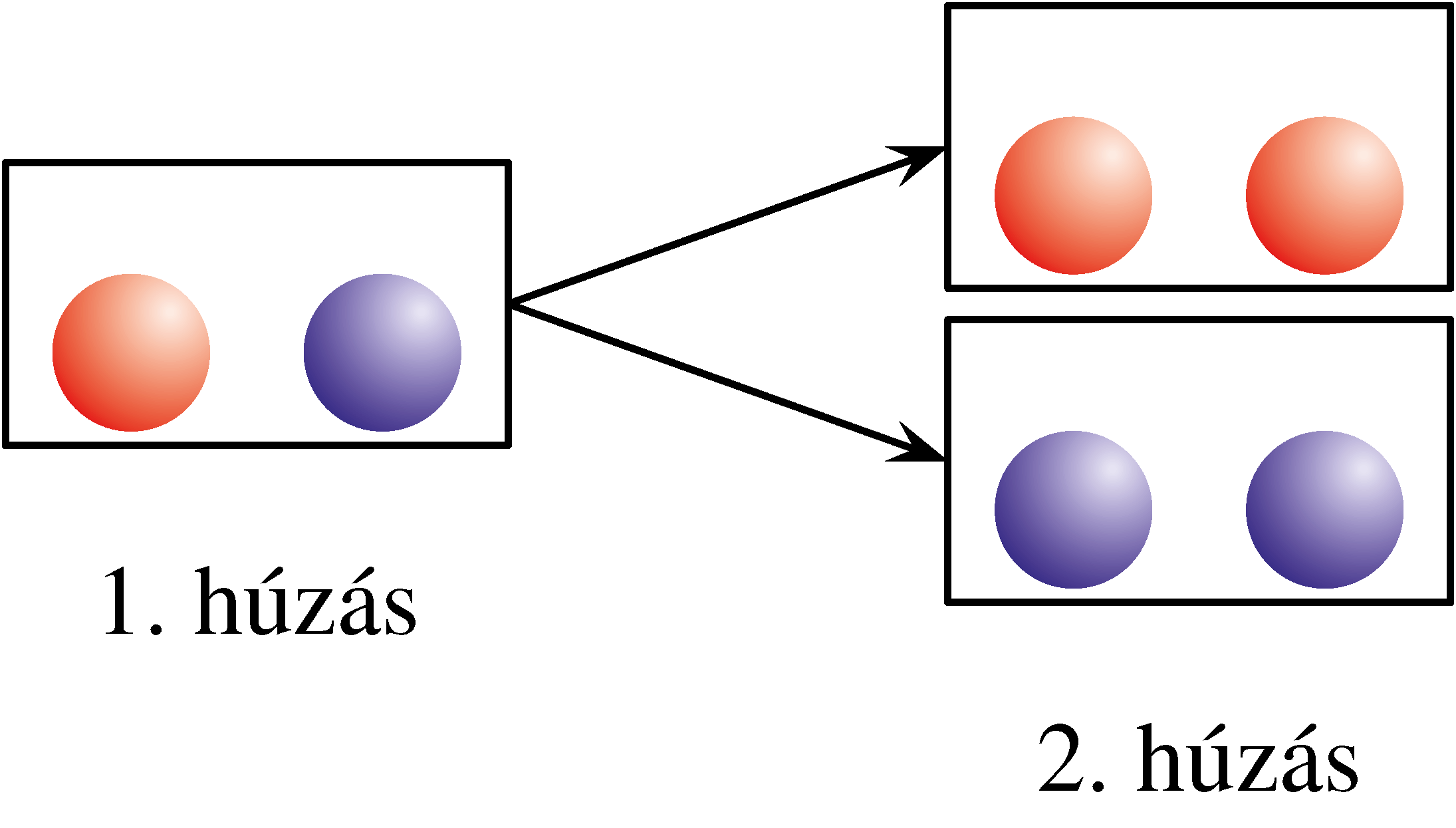
d) Ha Dia dobozt vált:

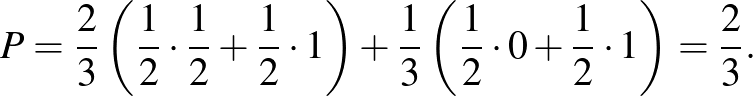
A kapott eredmények alapján tehát Diának az a legjobb stratégiája, ha mindkét golyót ugyanabból a dobozból húzza ki, és arra tippel, hogy a golyók színe azonos lesz. Ekkor nyerési esélye  .
.
Ez az írás a 2024-ben a békéscsabai Rátz László Vándorgyűlésen elhangzott szemináriumi foglalkozás alapján készült. A bemutatott feladatokkal felkelthetjük a középiskolás tanulók érdeklődését a valószínűségszámítási feladatok iránt. A cikkben közölt példákkal próbáltunk jól hasznosítható anyagot nyújtani a középiskolában tanító és a tehetséggondozásban résztvevő kollégáknak.
Fonyó Lajos – Fonyóné Németh Ildikó,
Keszthely











