„Akinek van szeme a matematikai látásra, az általában úgy emlékszik vissza
az iskolai matematikaórákra, mint folyamatos, masszív unatkozásra.
Akinek nincs erre szeme, az úgy, mint folyamatos, reménytelen frusztrációra.”
(Mérő László)
Hogyan lehet érdekesebb a matematikaóra?
Leülünk az online Honfoglalós párbajokhoz, és azt nehéz otthagyni. A matematikaóra is lehet ilyen, hogy leköt, odaköt, érdekes … Például egy matekos párbajjal.
Az óra témája mondjuk a háromszög területe. Legyen két játékos az osztályból, egyszerre kapják a kérdéseket ebben a témában, és aki gyorsabban ad helyes választ, övé a pont. A válaszadások után megbeszélik a megoldást. Így pöröghetnek a kvízkérdések, a szurkolótábor izgulhat a játékosokért. Csapatban is játszhatnak a gyerekek (mondjuk fiúk-lányok verseny). Lehetne párbaj az osztály és a tanár között is. De más játékokat is szervezhetünk. Persze ehhez gazdag és változatos feladatbank szükséges.
Azt szeretnénk, hogy a gyerekek átéljék a gondolkodás örömét, és minél többször megtapasztalják, milyen nagyszerű élmény önállóan rájönni valamire. Érdekes feladatokon jó gondolkodni.
Lehet jókat játszani, érdekessé válnak az órák. A gyerekek kíváncsiak lesznek a feladatok megoldására. Élvezik a tanulást, problémákat oldanak meg, együttműködnek egymással.
Ez nem ábrándozás. Kipróbáltuk, teszteltük, szeretik a gyerekek. A matekos párbaj élvezetes játék. És átvihető az online térbe is, az online játékok közé.
Weisz Ágoston és csapata (Alphacademy) elkészítette a párbajos játék első online változatát, az AlphaGame játékot, 1600 feladattal. Nyáron 3 hónapon át játszottak vele a gyerekek. A demo májusra elkészült, majd küldtek egy levelet iskoláknak, intézményvezetőknek. A gyerekek a tanároktól értesültek a játéklehetőségről. Gyorsan felfutott háromezer közelébe a regisztrált versenyzők száma, és egy időben átlagosan 20-40 játékos használta a játékot, délutánonként 100 körül.
A játékosok véleménye:
- Ez a játék a legjobb! Mindennap játszom vele suli után. Az osztálytársaimmal versenyzünk, hogy ki tud több kupát szerezni, és a matek is könnyebb lett nekem, amióta játszom. Tuti, hogy nyerhetek valami menő ajándékot!
- Nagyon szórakoztató játék, a kérdések érdekesek, és a motiváció is megvan, a nyereménynek köszönhetően. Gyors, az agyat kicsit megtornáztató körök. Tanulás előtt be tudja indítani az ember agyát! Nagyon értékelem, hogy nem szerencsén múlik, így mindenkinek ugyanannyi esélye van. Nekem nagyon tetszik!
- Meghívtam a legjobb barátomat, hogy próbálja ki ezt a játékot, és most mindketten imádjuk! Szerintem ez a legjobb játék, amit valaha játszottam. Nemcsak szórakoztató, de tényleg segít abban, hogy jobbak legyünk matekból. Plusz, imádom gyűjteni a kupákat és látni, hogy fejlődöm!
Az AlphaGame az első lépés. Látjuk, hogy életképes egy ilyen matematikai kvízjáték, de a fejlesztés erőforrásokat igényel ... Társak kellenek …
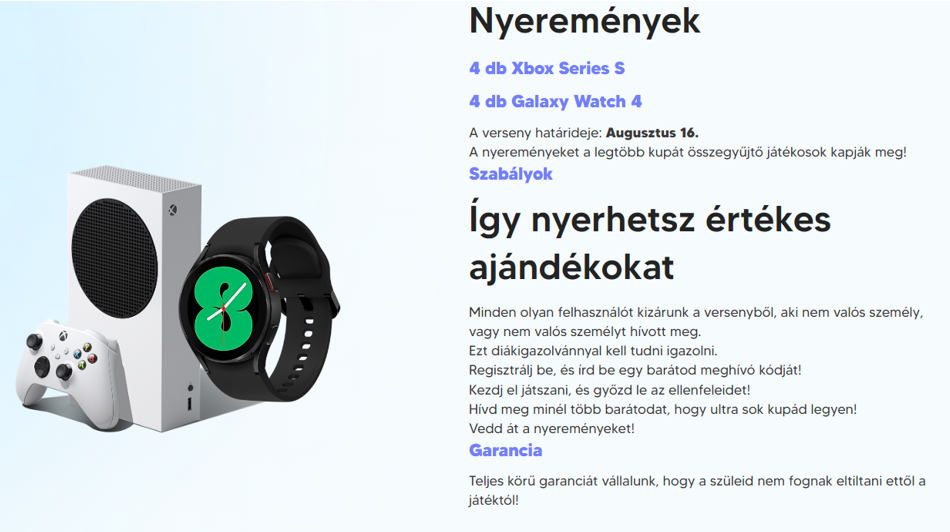
Ez a verseny az ügyességet és a kitartást díjazta, a hosszútávfutókat, azokat, akik három hónap alatt a legtöbb kupát (pontot) gyűjtötték. Itt egy kis ízelítő, hogyan is működött 2024 májusa és augusztusa között az a játék, amire a készítők teljes körű garanciát is vállaltak. (Teljes körű garanciát vállalunk, hogy a szüleid nem fognak eltiltani ettől a játéktól!)
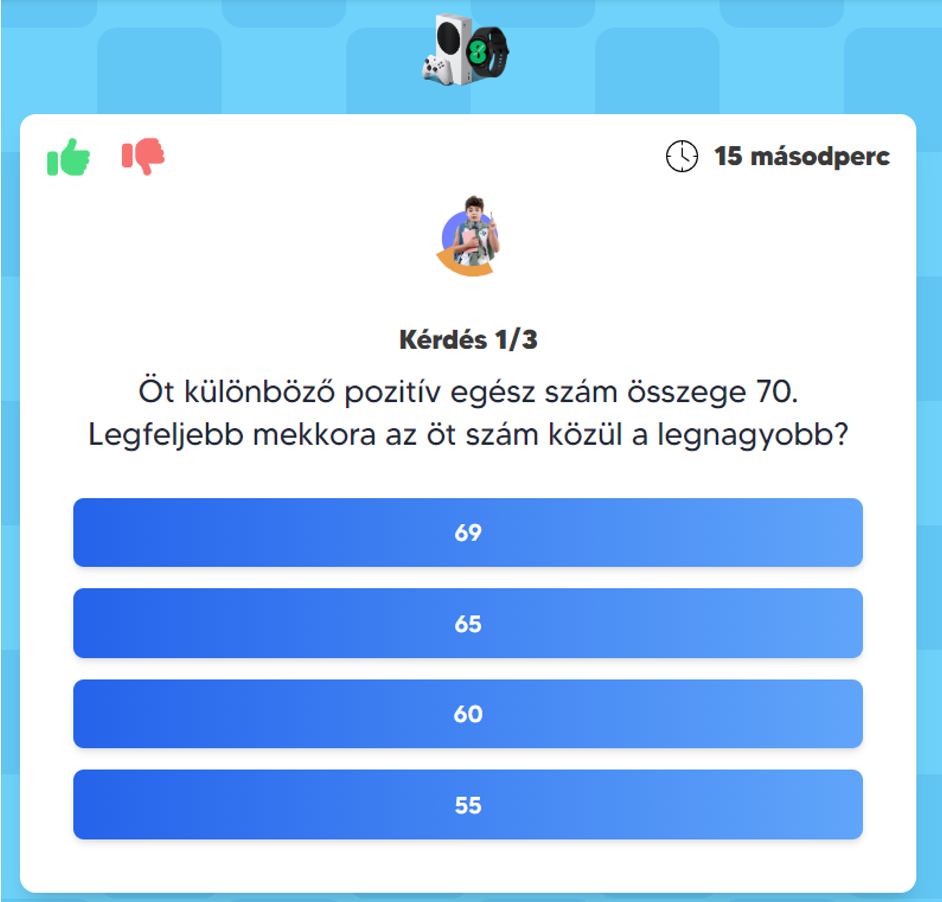
Egy ilyen versenyen mindenkinek lehet sikerélménye, ahogyan a Honfoglaló párbajaiban, vagy más online párbajozós játékban. Előnyeit más párbajokhoz képest pedig talán nem is kell ecsetelni (tudás, gyakorlás, hasznos időráfordítás…).
Ehhez fel kell építeni egy digitális feladatbankot, sokezer érdekes feladattal. Olyan feladatokkal, melyekre gyorsan lehet válaszolni. A feladatokat ellátjuk metaadatokkal, például hogy melyik korosztálynak ajánljuk, mi a témaköre, és további más hasznos címkékkel. A feladat nehézségét a játékok tapasztalataiból tudjuk mérni, és így jobban látjuk, mintha megjósolnánk azt. Így folyamatosan javítható, bővíthető a kezdeti feladatbank.
Vegyük észre, hogy a matematika tanításában milyen lehetőségek vannak előttünk, ezeket kár lenne kihagyni.
Látjuk, hogy visszaesett az érdeklődés a hagyományos versenyeinken. Népszerű lehet egy olyan új verseny, ami használja az online teret, a digitális lehetőségeket.
Egy megfelelően kialakított feladatbankból a tanár generálhat feladatlapot is az adott tanítási órára vagy szakköri foglalkozásra. Ha megadja a témát, az osztályt, a nehézséget, ehhez kaphat egy feladatsort a kidolgozott megoldásokkal, amit saját igénye, ízlése szerint átformálhat. A Feladatbank könnyíti a tanár munkáját.
Lehetne egy Tanulószoba, ahol a tanulók használják a Feladatbankot az önálló tanulásban. A Gyakorlótéren az aktuális leckéhez gyakorlófeladatokat kér, megnézheti azok megoldását, ezzel saját tempójában tanul a diák. A Küzdőtéren több tanuló közös játékban mérkőzhet egymással.
A Feladatbank egy ráépült mobilapplikációval segíthetné a tanítást, tanulást olyan módon, amelyről Lannert Judit beszélt egy riportban:
„A magyar iskolákban egy félévben írnak mondjuk három dolgozatot a diákok. Ha az elektronikus naplóba év elején bekerül egy kettes, a gyerek hiába ír utána két ötös dolgozatot, akkor sem kaphat félévkor jelest. Viszont a motivációját tökéletesen leépítjük ezzel a módszerrel. Ha azonban egész félévben pontszámokat gyűjthetne, ahogy az online videójátékokban, akkor nagy küzdelem árán felhozhatná a jegyét akár ötösre is.
Van, ahol inverz iskolát hoztak létre, figyelembe véve, hogy a személyre szabott oktatást a gépekkel lehet a legjobban elérni. A diákok otthon tanulnak, egy szoftver érzékeli, mi megy nekik, mi nem, és aszerint adja a feladatokat. Iskolába csak azért mennek be, hogy megtanulják a közösségi létet, megbeszéljék az anyagot, de a tanulás jellemzően egyéni tevékenység.”
Ha már nagyon nagy a Feladatbank, akkor használható a tanárképzésben és a tanárok önképzésére, továbbképzésére. Lehetne egy Versenyvizsga felület, ahol a vizsgára jelentkező valamilyen témakörben meg tudja méretni magát. Lennének szintvizsgák, ahogyan például a nyelvvizsgáknál.
A Feladatbankkal nemzeti értéket teremtünk. Segítséget adunk a diákoknak, segítjük a tanárokat. Ha megépítjük …
A szerző várja az ötlet iránt érdeklődők és a további fejlesztésben együttműködők jelentkezését.
Mintafeladatok a párbajhoz
1. Egy gazdának 11 báránya van. Közülük 9 kivételével mind elpusztult. Hány bárány maradt?
2. Legalább hány gyerek van abban a családban, ahol minden gyereknek van fiú és lánytestvére is?
3. Egy tó felszínén alga szaporodik. Minden nap megduplázódik az általa lefedett terület. A 32. napon befedi az egész tavat. Hányadik napon fedte be félig a tavat?
4. A tündérkirálynő 2 kortyot ivott a fiatalító vízből, és így újra 20 éves lett. Hány évet fiatalodott, ha minden korty után felére csökkent éveinek száma?
5. Melyik a huszadik kétjegyű szám?
6. Felírtam sorban a 12, 13, 14, …, 59, 60 számokat. Hány számot írtam fel?
7. Hány egész szám van 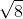 és
és 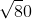 között?
között?
8. Hány prímszám van 90 és 100 között?
9. Hány olyan szám van, amely megegyezik a reciprokával?
10. Hány olyan kétjegyű szám van, amely akkora, mint számjegyei összegének négyzete?
11. Hány olyan kétjegyű szám van, amelyben a számjegyek összege páros szám?
12. Mennyi az 1, 3, 5, 7, ..., 99 számok összege?
13. Melyik az a legnagyobb kétjegyű szám, amelyben a számjegyek szorzata kisebb 7-nél?
14. Írd le a legkisebb, különböző számjegyekből álló négyjegyű páros számot.
15. Két szám egyike sem osztható 6-tal, a szorzatuk 36. Mennyi az összegük?
16. Hány olyan 6-ra végződő négyjegyű szám van, amely osztható 3-mal?
17. Egy utcában egymástól egyenlő távolságra 10 fát ültetünk. Az első és az utolsó fa közötti távolság 90 méter. Hány méter a távolság két szomszédos fa között?
18. Összeadtam egy háromjegyű szám számjegyeit, majd a kapott szám számjegyeit is. Mekkora az így kapható legnagyobb szám?
19. Egy nyolcjegyű szám első két számjegye 5 és 4, az utolsó jegye 9, és bármely négy egymás mellett álló számjegyének összege 20. Mennyi a nyolcjegyű szám számjegyeinek összege?
20. A 2002 úgynevezett palindrom szám, mivel visszafele olvasva ugyanannyi az értéke. Melyik a hozzá legközelebbi palindrom szám?
21. Négy egymást követő pozitív egész szám szorzata 3024. Mennyi ennek a négy számnak az összege?
22. Hány olyan szám van, amellyel a 103-at elosztva a maradék 13?
23. Mi az 501 legnagyobb, 501-nél kisebb osztója?
24. Melyik a legkisebb természetes szám, mely osztója a 24-nek, de nem osztója a 60-nak?
25. Hány olyan kétjegyű szám van, amelynek az 1-en kívül nincs páratlan osztója?
26. Hány olyan prímszám van 100 és 300 között, amelyben a számjegyek összege 15?
27. Hány olyan prímszám van 100 és 300 között, amelyben a számjegyek szorzata 15?
28. Hány jegyű a 45 legkisebb olyan pozitív többszöröse, melynek felírásában csak a 0 és 6 számjegyek szerepelnek?
29. Egy háromjegyű szám osztható 4-gyel. Legfeljebb mennyi lehet a szám számjegyeinek összege?
30. Hány olyan kétjegyű szám van, amelyben a számjegyek összege páros, és az 1-gyel nagyobb számban is páros a számjegyek összege?
31. Legfeljebb hány pontban metszheti egymást egy háromszög és egy négyszög, ha nincs közös oldalegyenesük?
32. Hány egyenes húzható egy kocka nyolc csúcsán át úgy, hogy minden egyenes két csúcsot tartalmazzon?
33. A kocka lapsíkjai hány részre osztják a teret?
34. A kocka minden lapját kiszíneztük, minden lapot egyszínűre úgy, hogy az élben szomszédos lapok különböző színűek. Legkevesebb hány színt kell ehhez használni?
35. A kocka minden lapját kiszíneztük, minden lapot egyszínűre úgy, hogy nincs két olyan azonos színű lap, amelyeknek van közös csúcsa. Legkevesebb hány színt kell ehhez használni?
36. Egy szolga évi bére 100 tallér és egy öltözet ruha volt. Nyolc hónap elteltével azonban elhagyta a helyét, megkapta a ruhát és még 20 tallért. Hány tallért ért a ruha?
37. Az iskolai síkfutó versenyen hárman indultak, Anna, Hanna és Panna. Hányféle olyan befutási sorrend alakulhat ki, amikor van holtverseny?
38. 20 asztaliteniszező között kieséses versenyt szervezünk. Minden forduló után a párokból a győztes jut tovább. Ha egy fordulóban valamelyik játékosnak nem jut ellenfél, úgy ő automatikusan tovább jut. Hány mérkőzést játszanak le, míg megtalálják a legjobb játékost?
39. A nyári táborozás során 8-szor esett az eső délelőtt vagy délután. Ha délelőtt esett, akkor délután nem esett. Összesen 5 esőtlen délelőtt és 7 esőtlen délután volt. Hány napig tartott a táborozás?
40. A mozi utolsó sora 12 székből áll, és néhány szék foglalt. Legtöbb hány foglalt szék lehet, ha minden szék mellett van üres szék?
Válaszok
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. |
| 9 | 4 | 31 | 60 | 29 | 25 | 6 | 1 | 2 | 1 |
| 11. | 12. | 13. | 14. | 15. | 16. | 17. | 18. | 19. | 20. |
| 45 | 2500 | 90 | 1024 | 13 | 300 | 10 | 10 | 40 | 1991 |
| 21. | 22. | 23. | 24. | 25. | 26. | 27. | 28. | 29. | 30. |
| 30 | 5 | 167 | 8 | 3 | 0 | 0 | 4 | 25 | 4 |
| 31. | 32. | 33. | 34. | 35. | 36. | 37. | 38. | 39. | 40. |
| 8 | 28 | 27 | 3 | 3 | 140 | 7 | 19 | 10 | 6 |
Róka Sándor
szerkesztő, Érintő, szerk.ematlap@gmail.com












