Bevezető gondolatok
A magyarországi matematikának egyik kiemelkedő területe a gráfelmélet. A nemzetközi szakkönyvekben, példatárakban nagyon gyakran találkozhatunk hivatkozásokkal magyar matematikusok tételeire, hazánkban kitűzött versenyfeladatok bemutatásával. Ezek a példák megmozgatják a fiatalok fantáziáját, hiszen a problémák megoldása szinte minden esetben valamilyen speciális felismerésen, különleges fogalomtársításon alapul, így komoly szellemi kihívást jelent még a matematikailag képzettek számára is.
Az iskolai tanórákon a diákok többsége általában csak a legalapvetőbb megoldási lehetőségekkel ismerkedik meg, és egyszerű feladatok megoldására válik alkalmassá. A tanulók rutinszerű példákat oldanak meg, adott tulajdonságú egyszerű gráfokat hoznak létre, és vizsgálják a létezés feltételeit. Ebben a cikkben más szempontok szerint vizsgáljuk meg a gráfokat. Áttekintjük, hogy a gráfok milyen széles körben lehetnek segítségünkre a problémák megoldásában. Tesszük ezt a színek segítségével úgy, hogy kiderüljön, hogy egy ilyen szemléltetéssel még a nehezebb feladatok is könnyebben megoldhatóvá válnak. Elkalandozunk a játékok, a sík- és a kombinatorikus geometria, a poliéderek, a versenyek világába, foglalkozunk optimális útvonalak, elhelyezkedések, kapcsolatrendszerek kialakításával. Eközben találkozunk a gráfelmélet legfontosabb összefüggéseivel, a fokszámokra vonatkozó ismeretekkel, a Turán-tétellel, a fákkal, a síkgráfokkal, az Euler-féle poliédertétellel, a Ramsey-problémákkal és a versenygráfokkal.
Az egyes módszerek segítségével nagyon változatos nehézségű és érdekes feladatok megoldását mutatjuk meg. A cikk végén azt is bemutatjuk, hogy hogyan készíthetünk mi magunk is nevezetes tételek segítségével feladatokat mások számára. Összességében egy jól hasznosítható anyagot szeretnénk adni a kollégáknak az iskolai szakköri munkához.
A cikkben a következő fogalmakat ismertnek tekintjük: gráf, teljes gráf, körmentes gráf, reguláris gráf, izolált pont, csúcs fokszáma.
A cikkben említett tételek bizonyítása megtalálható ezekben a művekben: Katona Gyula–Recski András–Szabó Csaba: A számítástudomány alapjai, Xiong Bin–Zheng Zhongyi: Graph Theory.
1. Gráfok alkalmazása nem várt helyzetekben
A következő két feladat arra mutat be egy-egy példát, hogy mennyire eredményesen használhatók a gráfok a játékelméletben. Segítségükkel tudatosan, gyorsan alakíthatunk ki egy játékhelyzetet, és könnyen indokolhatóvá válik az is, ha egy állás nem hozható létre.
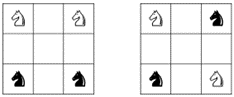
Egy 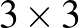 -as négyzetrács négy sarokmezőjében a bal oldali ábra szerint két világos és két sötét huszár áll. A huszároknak a sakk szabályai szerinti mozgatásával elérhető-e, hogy a bábuk a jobb oldali ábra szerinti helyzetbe kerüljenek, ha a lépések során a bábuk csak üres mezőkre ugorhatnak?
-as négyzetrács négy sarokmezőjében a bal oldali ábra szerint két világos és két sötét huszár áll. A huszároknak a sakk szabályai szerinti mozgatásával elérhető-e, hogy a bábuk a jobb oldali ábra szerinti helyzetbe kerüljenek, ha a lépések során a bábuk csak üres mezőkre ugorhatnak?
Megoldás:
Számozzuk meg a négyzetrács mezőit az alábbi ábra szerint:

Rendeljük hozzá a rács négyzeteihez egy gráf  ,
,  , ...,
, ...,  csúcsait, és kössük össze éllel azokat a csúcsokat, amelyekhez tartozó mezők elérhetők egymásból egy lóugrással. Ekkor a huszárok kezdeti és végső helyzetét is bejelölve az alábbi
csúcsait, és kössük össze éllel azokat a csúcsokat, amelyekhez tartozó mezők elérhetők egymásból egy lóugrással. Ekkor a huszárok kezdeti és végső helyzetét is bejelölve az alábbi 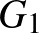 és
és 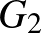 gráfokat kapjuk:
gráfokat kapjuk:
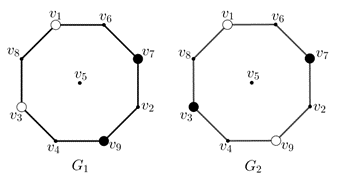
Mivel a huszároknak megfelelő csúcsokat a mozgatás mindig csak szomszédos üres csúcsba viheti, ezért a forgásirány szerinti sorrendjük a lépegetések során nem változhat meg.
Így a fehér–fehér–fekete–fekete huszár helyzete nem változhat át fehér–fekete–fehér–fekete sorrendre. Tehát a kívánt állapot nem érhető el.
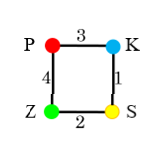
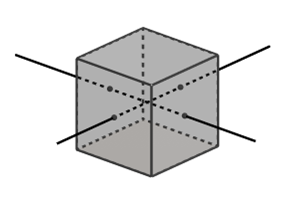
Egy 4 kockából álló logikai építőjáték elemeinek lapjai az alábbiak szerint vannak színezve:
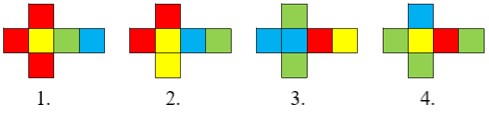
A játék célja az, hogy a kockákból úgy építsünk 4-szintes tornyot, hogy annak minden oldallapján az összes szín előforduljon.
Megoldás:
Rendeljünk az egyes kockákhoz egy-egy gráfot úgy, hogy ezen a kockák lapjainak a színezését át tudjuk tekinteni. Az egyes gráfoknak legyen négy csúcsa a négy színnek megfelelően. Két csúcs között akkor haladjon él, ha a kocka két szemben lévő lapja ilyen színű. Ha két ilyen lap azonos színű, akkor ezt az ábrán hurokél jelöli. Négy csúcsból és 3 élből álló gráfokat kapunk:
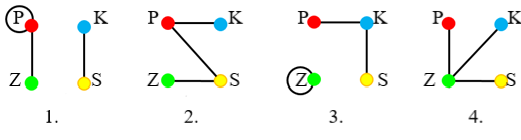
A négy gráfot egyesítve az alábbi  gráf adódik. Minden élre ráírjuk, hogy melyik kockából került az egyesített gráfba.
gráf adódik. Minden élre ráírjuk, hogy melyik kockából került az egyesített gráfba.

A feladat megoldásához olyan 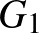 ,
, 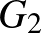 részgráfokat keresünk, amelyek megadják azokat a színeket, amelyek a torony elején-hátulján, illetve bal és jobb oldalán szerepelnek.
részgráfokat keresünk, amelyek megadják azokat a színeket, amelyek a torony elején-hátulján, illetve bal és jobb oldalán szerepelnek. 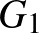 ,
, 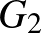 kiválasztásának szempontjai:
kiválasztásának szempontjai:
– A torony felépítésében mind a 4 kocka részt vesz, ezért 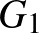 és
és  minden számozott gráfnak egy élét tartalmazza.
minden számozott gráfnak egy élét tartalmazza.
– A hasáb oldallapjain minden szín előfordul, ezért  és
és 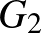 pontjai a
pontjai a  ,
, 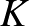 ,
, 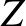 és
és  csúcsok.
csúcsok.
– A hasáb szemközti oldallapjain minden szín egyszer-egyszer, összesen kétszer szerepel, ezért a csúcsok másodfokúak, 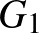 és
és 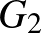 2-regulárisak.
2-regulárisak.
Egy lehetséges megoldás:
 |
 |
 |
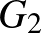 |
| Elöl – hátul | Balra – jobbra |
A két gráf mindegyikén szerepel az 1, 2, 3, 4 szám. Ez azt jelenti például, hogy az 1-es kockát úgy tegyük magunk elé, hogy elöl legyen a kék, hátul a sárga (vagy fordítva), balra legyen a piros, jobbra a zöld (vagy fordítva). A 2-es, 3-as, 4-es kocka elhelyezését hasonlóan olvashatjuk le a 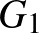 ,
, 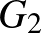 gráfokról. A második kocka elhelyezésétől kezdve figyelnünk kell arra, hogy azonos oldalra ne kerüljön kétszer egy szín. A kockát megfelelő tengelye/tengelyei körül elforgatva ez a probléma megoldható.
gráfokról. A második kocka elhelyezésétől kezdve figyelnünk kell arra, hogy azonos oldalra ne kerüljön kétszer egy szín. A kockát megfelelő tengelye/tengelyei körül elforgatva ez a probléma megoldható.
Ha ilyen módon felépítettünk egy tornyot, akkor a kockák sorrendje függőlegesen tetszőlegesen permutálható.
Az alábbi torony ilyen elvek szerint épült:
 |
hátsó lap | bal oldali lap | |
| 4. kocka | P | Z | |
| 3. kocka | K | K | |
| 2. kocka | Z | S | |
| 1. kocka | S | P |
2. Csúcsok fokszámának vizsgálata
Felhasznált tételek:
T1: Ha egy  gráfban a
gráfban a 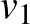 ,
, 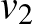 , ...,
, ..., 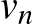 (
( 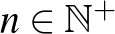 ) csúcsok fokszámai rendre
) csúcsok fokszámai rendre 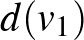 ,
, 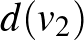 , ...,
, ..., 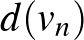 és az élek száma
és az élek száma  (
( 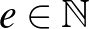 ), akkor
), akkor
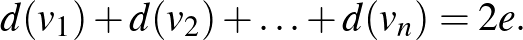
T2: Bármely  gráfban a páratlan fokú csúcsok száma páros.
gráfban a páratlan fokú csúcsok száma páros.
Egy háromszög csúcsai piros, kék és zöld színekkel vannak kiszínezve. A nagy háromszög belsejében elhelyezünk néhány pontot, és így azt több kisebb háromszögre bontjuk. Két kis háromszögnek lehet közös csúcsa, közös oldala, vagy lehetnek közös pont nélküliek is. A kis háromszögek csúcsait is kiszínezzük a piros, kék vagy zöld színek valamelyikével. Bizonyítsuk be, hogy bármilyen színezés esetén kapunk olyan háromszöget, amelynek csúcsai különböző színűek.
Megoldás:
Válasszunk ki egy pontot (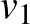 ) a nagy háromszögön kívül, és kössük össze azt a nagy háromszög piros-kék oldalára illeszkedő részháromszögének egy belső pontjával (
) a nagy háromszögön kívül, és kössük össze azt a nagy háromszög piros-kék oldalára illeszkedő részháromszögének egy belső pontjával (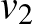 ). Továbbá keressük meg belül az összes piros-kék végpontú oldalt, és kössük össze az azokra illeszkedő két háromszögnek egy-egy belső pontját egy-egy szakasszal [az ábra szerint
). Továbbá keressük meg belül az összes piros-kék végpontú oldalt, és kössük össze az azokra illeszkedő két háromszögnek egy-egy belső pontját egy-egy szakasszal [az ábra szerint  ,
, 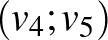 ,
, 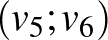 ].
].
Tekintsük a kiválasztott  pontokat egy
pontokat egy  gráf csúcsainak, a berajzolt szakaszokat
gráf csúcsainak, a berajzolt szakaszokat  éleinek.
éleinek.
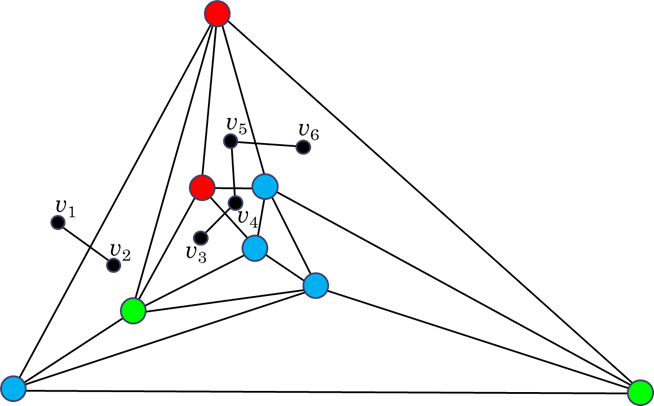


Ekkor a  gráf azon belső csúcsai, amelyek foka 1 és a nagy háromszög belsejében találhatók, egy háromszínű háromszög belsejében vannak.
gráf azon belső csúcsai, amelyek foka 1 és a nagy háromszög belsejében találhatók, egy háromszínű háromszög belsejében vannak.
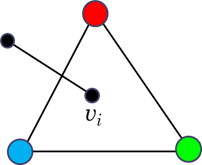
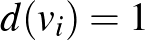
Másrészt  azon belső csúcsai, amelyek foka 2, egy piros-kék háromszög belsejében helyezkednek el.
azon belső csúcsai, amelyek foka 2, egy piros-kék háromszög belsejében helyezkednek el.

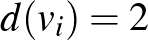
 csúcsainak fokszámát vizsgálva, mivel a nagy háromszögön kívüli csúcs foka 1, és a gráfban a páratlan fokú csúcsok száma páros, ezért
csúcsainak fokszámát vizsgálva, mivel a nagy háromszögön kívüli csúcs foka 1, és a gráfban a páratlan fokú csúcsok száma páros, ezért  tartalmaz még legalább egy 1-fokú csúcsot. A korábbi megállapításunk szerint ez a pont egy háromszínű háromszög belsejében helyezkedik el.
tartalmaz még legalább egy 1-fokú csúcsot. A korábbi megállapításunk szerint ez a pont egy háromszínű háromszög belsejében helyezkedik el.
3. Turán-tétel
Egyszerűbb formában:
Ha egy 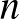 csúcspontú
csúcspontú  gráfban nincs
gráfban nincs 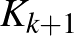 (teljes
(teljes 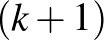 -es), akkor éleinek száma legfeljebb
-es), akkor éleinek száma legfeljebb
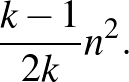
Teljes formában:
Ha 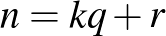 , ahol
, ahol 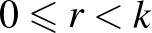 (
( ,
, 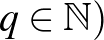 , és az
, és az 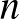 csúcspontú
csúcspontú  gráfban nincs
gráfban nincs 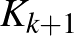 , akkor az élek
, akkor az élek  számára teljesül, hogy
számára teljesül, hogy
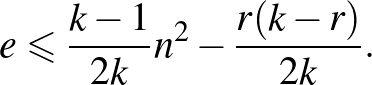
Az egyenlőség olyan 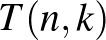 Turán-gráfra teljesül, amely
Turán-gráfra teljesül, amely  közös elem nélküli
közös elem nélküli  ,
,  , ...,
, ...,  ponthalmazból áll, ahol
ponthalmazból áll, ahol 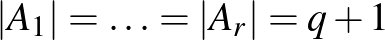 ,
, 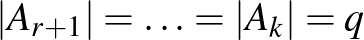 , és két pontot pontosan akkor kötünk össze, ha azok különböző ponthalmazokhoz tartoznak.
, és két pontot pontosan akkor kötünk össze, ha azok különböző ponthalmazokhoz tartoznak.
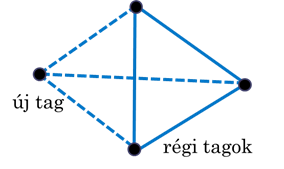
Egy bridzsklubnak van egy speciális szabálya, amely szerint 4 tag csak abban az esetben játszhat együtt, ha a párokon belül egyik játékos sem volt korábban a párjának partnere.
Egy találkozón 14 tag jelent meg, akik közül mindenki korábban 5 társának volt partnere. Az est folyamán 3 mérkőzés lejátszása után a tagok szomorúan tapasztalták, hogy a klubszabály miatt be kell fejezniük a játékot. Már készülnek a befejezésre, amikor beállít egy új tag, akit egyikük sem ismer. Mutassuk meg, hogy az ő érkezésével még legalább egy játék lejátszható.
Megoldás:
Rendeljük hozzá az eredetileg jelen levő 14 taghoz egy  gráf egy-egy csúcsát. Kössük össze éllel azokat a csúcsokat, amelyekhez tartozó emberek még nem volt partnerei egymásnak, majd vizsgáljuk a gráf
gráf egy-egy csúcsát. Kössük össze éllel azokat a csúcsokat, amelyekhez tartozó emberek még nem volt partnerei egymásnak, majd vizsgáljuk a gráf 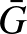 komplementerét.
komplementerét.
Figyelembe véve, hogy a 14 személy mindegyikének korábban 5 partnere volt, és az est folyamán az új tag érkezéséig már 3 mérkőzést lejátszottak, ezért 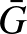 éleinek száma:
éleinek száma:
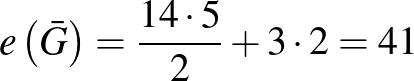 , és
, és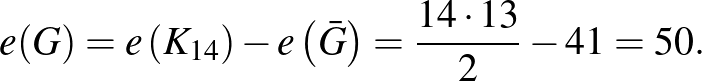
Az új tag érkezésével akkor nyílik lehetőség új partira, ha  tartalmaz háromszöget. A Turán-tétel alapján, ha
tartalmaz háromszöget. A Turán-tétel alapján, ha  -ben nincs
-ben nincs 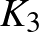 , akkor
, akkor
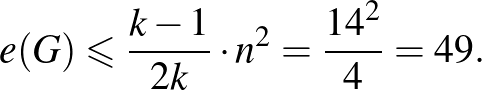
Mivel  -ben az élek száma meghaladja a 49-et, így
-ben az élek száma meghaladja a 49-et, így  tartalmaz háromszöget. Ehhez a háromszöghöz tartozó személyek és az új tag között tehát lebonyolítható a szabályoknak megfelelő mérkőzés.
tartalmaz háromszöget. Ehhez a háromszöghöz tartozó személyek és az új tag között tehát lebonyolítható a szabályoknak megfelelő mérkőzés.
4. Fagráfok
Fontosabb definíciók, tételek:
D1: Az összefüggő, körmentes gráfokat fáknak nevezzük.
T1: Minden legalább 2 pontú 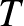 fagráfban van legalább 2 elsőfokú pont.
fagráfban van legalább 2 elsőfokú pont.
T2: Ha a 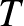 fagráf csúcsainak száma
fagráf csúcsainak száma 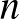 (
( 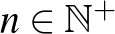 ), akkor éleinek száma
), akkor éleinek száma 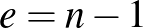 .
.
T3: Legyen a 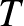 fagráf csúcsainak száma
fagráf csúcsainak száma 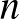 , éleinek száma
, éleinek száma  . Ekkor az alábbi tulajdonságok ekvivalensek egymással:
. Ekkor az alábbi tulajdonságok ekvivalensek egymással:
a) 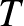 fagráf,
fagráf,
b) 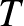 körmentes és
körmentes és 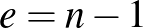 ,
,
c) 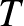 összefüggő és
összefüggő és 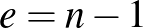 .
.
Egy 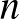 csúcsú teljes gráf éleit Dia és Viki a megadott sorrend szerint felváltva színezi ki pirosra. Az veszít, aki először hoz létre piros kört. Melyik lánynak van nyerő stratégiája?
csúcsú teljes gráf éleit Dia és Viki a megadott sorrend szerint felváltva színezi ki pirosra. Az veszít, aki először hoz létre piros kört. Melyik lánynak van nyerő stratégiája?
Megoldás:
A feladatban szereplő játéknak csak  esetén van értelme, hiszen
esetén van értelme, hiszen 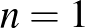 ,
,  esetén senki sem veszít, tehát a játék döntetlen eredménnyel ér véget.
esetén senki sem veszít, tehát a játék döntetlen eredménnyel ér véget.
Használjuk fel a feladat megoldásához az alábbi két gráfelméleti tételt:
– Egy 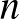 csúcsú összefüggő gráfnak legalább
csúcsú összefüggő gráfnak legalább 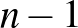 éle van.
éle van.
– Egy 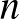 csúcsú körmentes gráfnak legfeljebb
csúcsú körmentes gráfnak legfeljebb 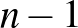 éle van.
éle van.
Azt fogjuk belátni, hogy  esetben helyes játék esetén az veszít, akinek az
esetben helyes játék esetén az veszít, akinek az 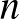 . élt kell pirosra színeznie. Állításunk igazolásához elég belátni, hogy ha
. élt kell pirosra színeznie. Állításunk igazolásához elég belátni, hogy ha 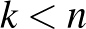 , akkor az a játékos, aki a
, akkor az a játékos, aki a 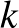 élt színezi, még meg tudja tenni, hogy ne ő hozzon létre piros élekből álló kört.
élt színezi, még meg tudja tenni, hogy ne ő hozzon létre piros élekből álló kört.
Tekintsük azt a 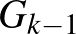 gráfot, amit az addig kiszínezett
gráfot, amit az addig kiszínezett 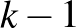 él alkot az
él alkot az 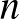 csúccsal.
csúccsal.
Ha 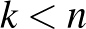 , akkor
, akkor 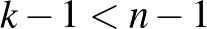 , így
, így 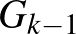 nem összefüggő. Ez azt jelenti, hogy szétbomlik két vagy több
nem összefüggő. Ez azt jelenti, hogy szétbomlik két vagy több 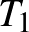 ,
, 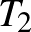 , ...,
, ...,  fára, amelyek között nem fut él.
fára, amelyek között nem fut él.
Pl.  ,
, 
Az éppen következő játékosnak nem kell mást tennie, mint két fa egy-egy pontját kell összekötnie egy piros éllel. Ha 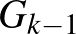 -ben nem volt piros kör, akkor
-ben nem volt piros kör, akkor 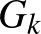 -ban sem lesz, mivel a kör kialakításához fel kellene használni az újonnan behúzott élt, illetve a két fa között kellene lennie még egy összekötő élnek. Ilyen pedig nincs.
-ban sem lesz, mivel a kör kialakításához fel kellene használni az újonnan behúzott élt, illetve a két fa között kellene lennie még egy összekötő élnek. Ilyen pedig nincs.
Így beláttuk, hogy ha az egyik leánynak a 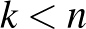 sorszámú élt kell kiszíneznie, akkor el tudja kerülni a piros kör kialakulását. Az a játékos viszont, akinek az
sorszámú élt kell kiszíneznie, akkor el tudja kerülni a piros kör kialakulását. Az a játékos viszont, akinek az 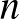 . él jut, ezt már nem tudja megtenni. Ezért helyes stratégia esetén páros
. él jut, ezt már nem tudja megtenni. Ezért helyes stratégia esetén páros 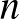 -re Dia, páratlanra pedig Viki nyer.
-re Dia, páratlanra pedig Viki nyer.
5. Euler-vonal
Felhasználható definíciók, tételek:
D1: Vonalnak nevezzük egy gráf éleinek egymáshoz csatlakozó sorozatát, amelyben minden él legfeljebb egyszer szerepelhet, de lehetnek olyan pontok, amelyek többször is előfordulnak.
D2: Euler-vonalnak nevezünk egy gráfban egy vonalat, ha az a gráf minden élén áthalad. Az Euler-vonal lehet nyitott, ha a kezdő- és végpontja nem azonos, és lehet zárt, ha kezdő- és végpontja megegyezik.
T1: Izolált pontot nem tartalmazó gráfban akkor és csak akkor van zárt Euler-vonal, ha a gráf összefüggő és minden pont fokszáma páros.
T2: Izolált pontot nem tartalmazó gráfban akkor és csak akkor van nyitott Euler-vonal, ha a gráf összefüggő és két pont fokszáma páratlan, a többi pont fokszáma páros.
Az ábra szerint Atom Anti és Zé, a két hangya az 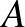 és
és 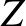 pontokban állnak. Azt mondja Anti Zé-nek: „Versenyezzünk, nézzük meg, hogy melyikünk halad át először a 9 élen és ki ér előbb a
pontokban állnak. Azt mondja Anti Zé-nek: „Versenyezzünk, nézzük meg, hogy melyikünk halad át először a 9 élen és ki ér előbb a 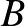 csúcsba.” A két hangya egyszerre indul, és azonos sebességgel halad. Ki nyeri meg a versenyt?
csúcsba.” A két hangya egyszerre indul, és azonos sebességgel halad. Ki nyeri meg a versenyt?

Megoldás:
Tekintsük a pontokat egy  gráf csúcsainak, a köztük húzott szakaszokat pedig az éleinek.
gráf csúcsainak, a köztük húzott szakaszokat pedig az éleinek.  összefüggő, és az egyes csúcsok fokszámai:
összefüggő, és az egyes csúcsok fokszámai: 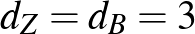 ,
, 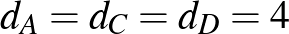 .
.
Tehát  -ben pontosan két páratlan fokú csúcs van (
-ben pontosan két páratlan fokú csúcs van (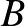 és
és 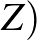 . Így T2 alapján a gráfban van nyílt Euler-vonal, amelynek két végpontja
. Így T2 alapján a gráfban van nyílt Euler-vonal, amelynek két végpontja  és
és  .
.
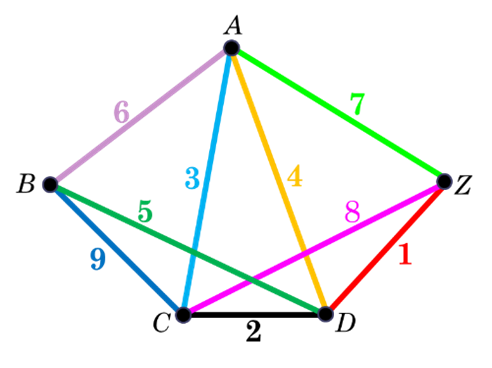
Ezért, ha Zé például  -ből indulva a
-ből indulva a 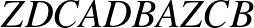 nyílt Euler-vonalon halad, akkor 9 él érintésével eljuthat
nyílt Euler-vonalon halad, akkor 9 él érintésével eljuthat 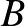 -be (lásd a fenti ábrát). Anti a páros fokszámú
-be (lásd a fenti ábrát). Anti a páros fokszámú 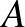 pontból indul, így ő nem juthat el élismétlés nélkül
pontból indul, így ő nem juthat el élismétlés nélkül 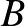 -be. Tehát a megfelelő útvonalválasztás esetén Zé nyeri meg a versenyt.
-be. Tehát a megfelelő útvonalválasztás esetén Zé nyeri meg a versenyt.
6. Hamilton-kör
Fontosabb definíciók, tételek:
D: Egy  gráfban egy kört Hamilton-körnek nevezünk, ha
gráfban egy kört Hamilton-körnek nevezünk, ha  minden pontját pontosan egyszer tartalmazza.
minden pontját pontosan egyszer tartalmazza.
T1 (Ore-tétel): Legyen  egyszerű gráf csúcsainak száma
egyszerű gráf csúcsainak száma 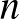 (
(  ,
, 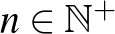 ). Ha bármely
). Ha bármely 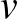 ,
, 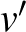 nem szomszédos csúcspár esetén
nem szomszédos csúcspár esetén 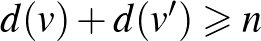 , akkor
, akkor  tartalmaz Hamilton-kört.
tartalmaz Hamilton-kört.
T2 (Dirac-tétel): Legyen  egyszerű gráf csúcsainak száma
egyszerű gráf csúcsainak száma 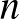 (
(  ,
, 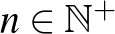 ). Ha a gráfban minden pont foka legalább
). Ha a gráfban minden pont foka legalább 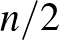 , akkor a gráfban létezik Hamilton-kör.
, akkor a gráfban létezik Hamilton-kör.
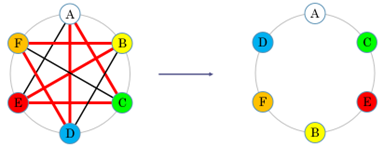
Egy kör alakú asztal körül legalább 5 ember ül. Lehetséges-e, hogy úgy módosítsuk az ülésrendet, hogy mindenkinek két új szomszédja legyen?
Megoldás:
5 fő esetén egy lehetséges megoldás:
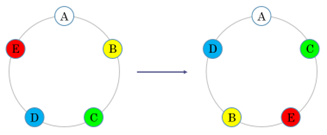
5-nél több személy esetén rendeljük a társaság tagjaihoz egy gráf csúcsait, és kössük össze éllel azokat a csúcsokat, amelyekhez tartozó emberek az eredeti helyzet szerint nem voltak szomszédok. Így olyan  gráfot kapunk, amelyben minden csúcs foka
gráfot kapunk, amelyben minden csúcs foka  (
(  ,
, 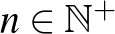 ). Ekkor a gráfban bármely két csúcs fokszámának összege
). Ekkor a gráfban bármely két csúcs fokszámának összege 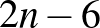 .
.
 esetén
esetén 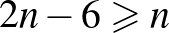 , és az Ore-tétel miatt
, és az Ore-tétel miatt  tartalmaz Hamilton-kört. Ez alapján alakítható ki a helyes ülésrend. Az ábra
tartalmaz Hamilton-kört. Ez alapján alakítható ki a helyes ülésrend. Az ábra  esetén mutatja be a megoldást:
esetén mutatja be a megoldást:
7. Síkba rajzolható gráfok
D: Egy gráf síkba rajzolható, ha lerajzolható a síkban úgy, hogy élei kizárólag a csúcspontokban találkoznak.
Euler-formula: Ha adott egy véges összefüggő síkgráf, ahol 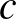 a csúcsok,
a csúcsok,  az élek,
az élek, 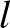 pedig a tartományok számát jelöli, beleértve a külső nagy területet is, akkor
pedig a tartományok számát jelöli, beleértve a külső nagy területet is, akkor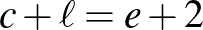
Adott egy körön 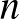 pont (
pont (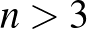 ,
, 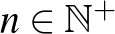 ). Bármelyik két pontot összekötjük egy-egy szakasszal. Ezen szakaszok között nincs 3 olyan, amelyek a körön belül egy pontban metszik egymást. Határozzuk meg a körön belül kialakult tartományok számát.
). Bármelyik két pontot összekötjük egy-egy szakasszal. Ezen szakaszok között nincs 3 olyan, amelyek a körön belül egy pontban metszik egymást. Határozzuk meg a körön belül kialakult tartományok számát.
Megoldás:
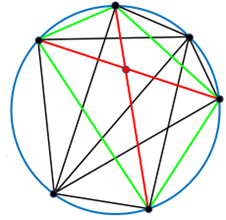
A kör 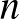 ívének eltávolítása után egy egyszerű síkgráfot kapunk, amelynek csúcsai a körön levő pontok és a szakaszok körön belüli metszéspontjai.
ívének eltávolítása után egy egyszerű síkgráfot kapunk, amelynek csúcsai a körön levő pontok és a szakaszok körön belüli metszéspontjai.
A körön levő pontok közül bármelyik 4 pontosan egy belső metszéspontot határoz meg, így
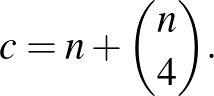
A körön levő pontok mindegyikéhez 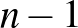 , a belső pontokhoz 4-4 él tartozik, és minden élnek két végpontja van, ezért
, a belső pontokhoz 4-4 él tartozik, és minden élnek két végpontja van, ezért
![$\displaystyle e=\frac{1}{2}\cdot \left[n(n-1)+4\binom{n}{4}\right].
$](/images/stories/latexuj/2022-10/2022-10-sokszinnel/img83.png)
A síkgráfokra vonatkozó Euler-formula alapján a tartományok száma:
![$\displaystyle \ell'=e+2-c=\left[\frac{n\left(n-1\right)}{2}+2\binom{n}{4}\right]+2-\left[n+\binom{n}{4}\right].
$](/images/stories/latexuj/2022-10/2022-10-sokszinnel/img84.png)
Az így kimaradt tartományokhoz hozzáadva a körívek által határolt 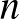 tartományt és levonva a körön kívüli részt:
tartományt és levonva a körön kívüli részt:
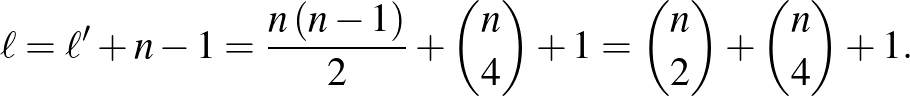
8. Ramsey-számok
Fontosabb ismeretek:
T (Ramsey-tétel): Adott 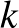 és
és 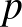 pozitív egészekhez létezik egy olyan legkisebb
pozitív egészekhez létezik egy olyan legkisebb  szám, hogy bármely
szám, hogy bármely 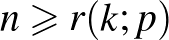 (
( 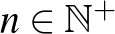 ) esetén az
) esetén az 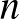 pontú
pontú  teljes gráf éleit két színnel – kékkel és pirossal – kiszínezve van a gráfban egy kék
teljes gráf éleit két színnel – kékkel és pirossal – kiszínezve van a gráfban egy kék 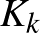 vagy egy piros
vagy egy piros 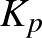 .
.
T1: 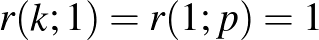
T2: 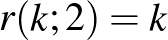 ,
, 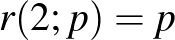
T3: 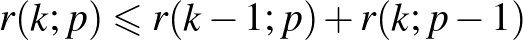
T4: (Erdős–Szekeres): 
Néhány Ramsey-szám:
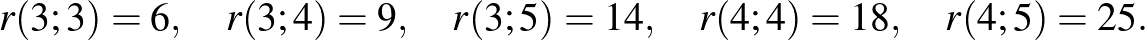
Az 1, 2, 3, 4, 5 számokat véletlenszerűen két csoportba (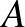 és
és 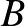 ) osztjuk. Bizonyítsuk be, hogy az egyik csoportba kerül két olyan szám, amelyek különbsége megegyezik a csoport egyik számával.
) osztjuk. Bizonyítsuk be, hogy az egyik csoportba kerül két olyan szám, amelyek különbsége megegyezik a csoport egyik számával.
Megoldás:
Az 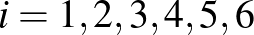 számokhoz rendeljük hozzá egy
számokhoz rendeljük hozzá egy  gráf
gráf 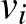 csúcsait. Bármely
csúcsait. Bármely 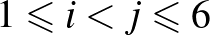 esetén kössük össze a
esetén kössük össze a 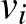 ,
, 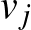 csúcsokat kék éllel, ha
csúcsokat kék éllel, ha 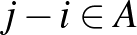 , és pirossal, ha
, és pirossal, ha 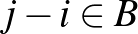 . Így egy kétszínű
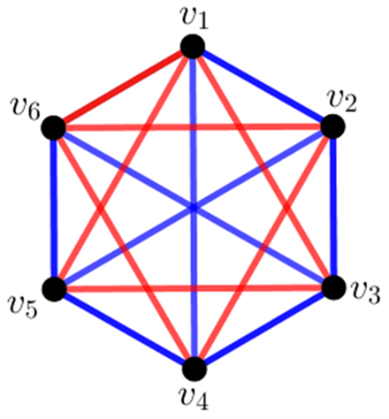
. Így egy kétszínű  teljes gráfot kapunk, amely
teljes gráfot kapunk, amely 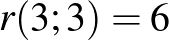 miatt tartalmaz monokromatikus háromszöget. Legyenek ennek csúcsai
miatt tartalmaz monokromatikus háromszöget. Legyenek ennek csúcsai 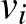 ,
, 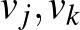 (
( 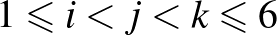 ). Ekkor az
). Ekkor az 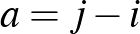 ,
, 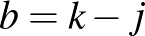 ,
,  számok egy csoportban vannak, és
számok egy csoportban vannak, és
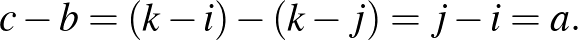
Például 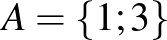 ,
,  esetén:
esetén:
Piros háromszög 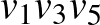 , (
, (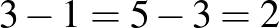 ,
, 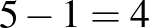 ) és
) és 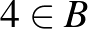 ,
, 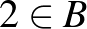 és
és 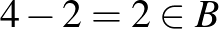 .
.
9. Versenygráfok
Fontosabb ismeretek:
D: Egy gráfot irányított versenygráfnak nevezünk, ha 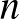 (
( 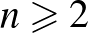 ,
, 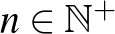 ) csúcsot tartalmaz, és bármely két csúcsot pontosan egy irányított él köt össze.
) csúcsot tartalmaz, és bármely két csúcsot pontosan egy irányított él köt össze.
Jelölése: 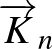 .
.
Az él a győztestől mutat a vesztes felé.
A 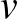 csúcs kifoka az adott csúcsból kiinduló, befoka pedig az oda befutó élek száma. Jelölésük:
csúcs kifoka az adott csúcsból kiinduló, befoka pedig az oda befutó élek száma. Jelölésük: 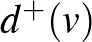 , illetve
, illetve 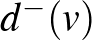 .
.

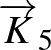 ,
, 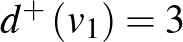 ,
, 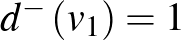
T1: Legyenek 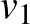 ,
, 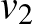 , ...,
, ..., 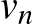 egy
egy 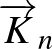 versenygráf csúcsai. Ekkor
versenygráf csúcsai. Ekkor
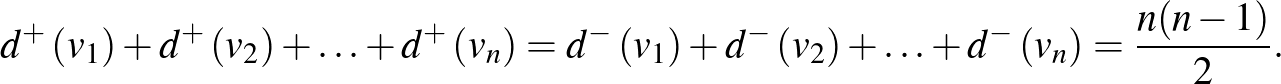
T2: Egy versenygráfban mindig létezik olyan csúcs, ahonnan vezet irányított út bármely más csúcsba. Az ilyen utak maximális hossza 2.
T3: A 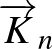 versenygráf mindig tartalmaz
versenygráf mindig tartalmaz 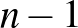 hosszú Hamilton-utat.
hosszú Hamilton-utat.
T4: Egy 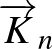 versenygráf (
versenygráf (  ,
, 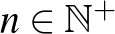 ) akkor és csak akkor tartalmaz kört, ami háromszög, ha létezik két olyan
) akkor és csak akkor tartalmaz kört, ami háromszög, ha létezik két olyan 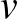 és
és 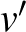 csúcs, melyekre teljesül, hogy
csúcs, melyekre teljesül, hogy
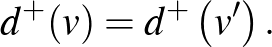
A tételek alapján nagyon könnyen készíthetünk magunk is versenyfeladatokat. A feladatok megoldása a tételek bizonyítása szerint történik, amelyekre a cikk terjedelme miatt nem térünk ki. Lássuk tehát a versenyeken kitűzhető, nem túl könnyű példákat!
Egy egyfordulós körmérkőzéses tornán 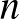 (
( 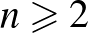 ,
, 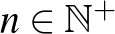 ) játékos vesz részt, és mindenki a többiekkel egy-egy mérkőzést játszik. A mérkőzéseken nincs döntetlen eredmény. Bizonyítsuk be, hogy a versenyzők között van olyan személy, hogy ő, az általa legyőzött személyek és az általa legyőzött személyek által legyőzött ellenfelek az összes sportolót tartalmazzák.
) játékos vesz részt, és mindenki a többiekkel egy-egy mérkőzést játszik. A mérkőzéseken nincs döntetlen eredmény. Bizonyítsuk be, hogy a versenyzők között van olyan személy, hogy ő, az általa legyőzött személyek és az általa legyőzött személyek által legyőzött ellenfelek az összes sportolót tartalmazzák.
Megoldás: T2-ből következik az állítás.
Egy asztalitenisz tornán bármely két játékos pontosan egyszer játszik a többi versenyzővel. Bizonyítsuk be, hogy a játékosokat lehet úgy sorszámozni, hogy minden játékos legyőzte a közvetlenül utána következőt.
Megoldás: T3-ból következik az állítás.
Egy körmérkőzéses egyfordulós röplabda tornán 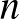 (
(  ,
, 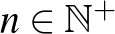 ) csapat vesz részt. A tornán egyetlen csapat sem győzte le az összes ellenfelét. Bizonyítsuk be, hogy a résztvevők között található három olyan
) csapat vesz részt. A tornán egyetlen csapat sem győzte le az összes ellenfelét. Bizonyítsuk be, hogy a résztvevők között található három olyan 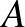 ,
, 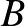 ,
,  csapat, hogy
csapat, hogy 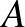 legyőzte
legyőzte 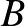 -t,
-t, 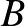 legyőzte
legyőzte  -t és
-t és  legyőzte
legyőzte 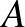 -t.
-t.
Megoldás: A skatulyaelvből és T4-ből következik az állítás.
Ez az írás a 2022-ben az egri Rátz László Vándorgyűlésen elhangzott szemináriumi foglalkozás alapján készült. A bemutatott feladatokkal felkelthetjük a középiskolás tanulók érdeklődését a gráfelméleti feladatok iránt. A cikkben közölt példák között amerikai, kínai, magyar versenyfeladatok mellett saját feladatok is szerepelnek. Ezekkel próbáltunk jól hasznosítható anyagot biztosítani a középiskolában tanító és a tehetséggondozásban résztvevő kollégáknak.









