Hitel, törlesztőrészlet, járadékszámítás

Miért tanulunk kamatszámítást?

A bankbetétek, hitelek kamatozása az úgynevezett kamatos kamatozás szerint történik, amelynek matematikai alapját a mértani sorozatok jelentik. Ahhoz, hogy az alkalmazott matematikai modelleket és számításokat mindenki megértse, fel kell idézni a középiskolában a mértani sorozatról tanult ismereteket. Aki tisztában van a mértani sorozat tulajdonságaival és összegképletével, az átugorhatja a bevezetést.

Bevezetés

Mértani sorozat

Definíció. Mértani sorozatnak nevezzük azt a számsorozatot, amelyben [a másodiktól kezdve] bármelyik tagnak és az azt megelőző tagnak a hányadosa állandó. Ezt az állandó hányadost 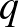$q$ -val jelöljük, és a mértani sorozat hányadosának (kvóciensének) nevezzük.

A definícióból következik a mértani sorozat rekurzív képzési szabálya: 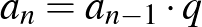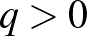${a_{n}=a_{n-1}\cdot q}$ . [ $q>0$ esetén a tagok előjele azonos, 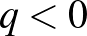$q<0$ esetén a tagok előjele váltakozó.]

Teljes indukcióval könnyen belátható, hogy a mértani sorozat 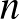$n$ -edik tagját az 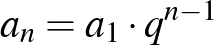$a_{n}=a_{1}\cdot q^{n-1}$ képlettel adhatjuk meg.

Megjegyzés. Ez a definíció kizárja az 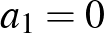$a_{1}=0$ , illetve 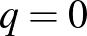$q=0$ eseteket. Ekkor ugyanis vagy a 0, 0, 0, ..., vagy az 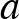$a$ , 0, 0, 0, ... típusú sorozatokat kapnánk, azonban kényelmi szempontok miatt ezeket nem tekintjük mértani sorozatoknak.

Egyszerűen megmutatható, hogy 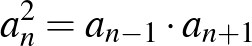$a_{n}^{2}=a_{n-1}\cdot a_{n+1}$ . Nem mondhatjuk azonban [a számtani sorozattal analóg módon], hogy a mértani sorozat egy tagja az őt közrefogó elemek mértani közepe, hisz a mértani sorozatnak negatív tagjai is lehetnek, így a fenti kijelentésünk nem lenne összhangban a mértani közép definíciójával. Helyesebb tehát csak a pozitív tagú mértani sorozatokra szorítkozni ebben az esetben. Ekkor megállapíthatjuk, hogy a pozitív számokból álló mértani sorozat bármely három egymást követő elemére igaz, hogy a két szélső mértani közepe egyenlő a középső taggal.

Megjegyzés. Természetesen mértani sorozatról beszélünk abban az esetben is, ha 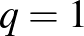$q=1$ .

A mértani sorozat első 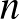tagjának összege

Idézzük fel a gimnáziumi első osztályos tananyagból az 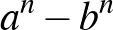$a^{n}-b^{n}$ kifejezés szorzattá alakítását!

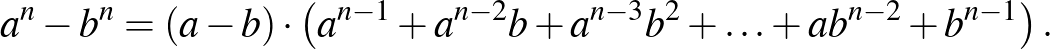
$\displaystyle a^{n}-b^{n}=(a-b)\cdot \left(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+\ldots+ab^{n-2}+b^{n-1}\right).$

A mértani sorozat első 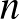$n$ tagjának összegzésekor az alábbi összeget kell kiszámítanunk:

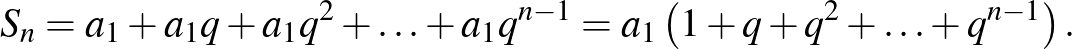
$\displaystyle S_{n}=a_{1}+a_{1}q+a_{1}q^{2}+\ldots+a_{1}q^{n-1}=a_{1}\left(1+q+q^{2}+\ldots+q^{n-1}\right).$

Ha a zárójeles kifejezést összevetjük a fenti szorzattal, akkor látható, hogy ott 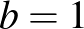$a=q$ , $b=1$ helyettesítéssel hasonlót kapunk:

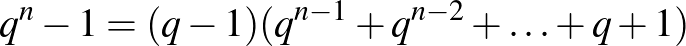$\displaystyle q^{n}-1=(q-1)(q^{n-1}+q^{n-2}+\ldots+q+1)$ .

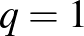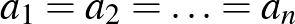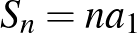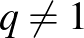Ha $q=1$ , akkor természetesen $a_{1}=a_{2}=\ldots=a_{n}$ , azaz $S_{n}=na_{1}$ , ha $q\ne 1$ , akkor pedig 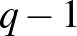$q-1$ -gyel leoszthatunk:

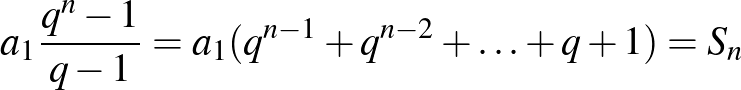$\displaystyle a_{1}\frac{q^{n}-1}{q-1}=a_{1}(q^{n-1}+q^{n-2}+\ldots+q+1)=S_{n}$ .

Ezeket az összefüggéseket fogjuk a továbbiakban felhasználni.

Kamatszámítás

Mi a kamat?

A kamat egyszerűen fogalmazva a pénz (helyesebben tőke) szolgáltatásainak az ára. A kamat (helyesebben szólva inkább a hozam) a befektető jutalma azért, hogy tőkéjét lekötve elhalasztja a fogyasztását. A kamat fogalma szorosan összefügg a pénz időértékével. A pénz időértéke legegyszerűbben kifejezve annyit jelent, hogy egy forint „ma” többet ér, mint ugyanez az egy forint „holnap” (a „ma” alatt itt a jelent, míg a „holnap” alatt a jövőt kell érteni), mert a mai forint befektethető és kamatozik. Másként kifejezve a befektető a kamatot mint jutalmat azért kapja, mert a mai biztos forintot felváltja egy jövőbeni kockázatos forintra. (Forrás: https://sevenday.ewk.hu/kamatos-kamat-csodaja/)

Kamatos kamat

Egy adott év elején befizetünk a bankba 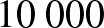$10\;000$ Ft-ot. A bank évi 5% kamatos kamatot ad a betét után, a kamatot mindig az év végén írják hozzá a betétünkhöz. Hány forintunk lesz a bankban 20 év elteltével?

Megoldás. A bank által adott kamattal minden év végén a pénzünk 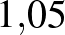$1{,}05$ -szörösére változik. 20 év elteltével a kamattal növelt összeg 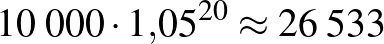$10\;000\cdot 1{,}05^{20}\approx 26\;533$ Ft lesz.

Definíció. Évi kamatos kamat: a kamat jóváírása évente egyszer történik, év végén. A kamatláb az egész évre érvényes kamatlábbal egyezik meg.

Definíció. Havi kamatos kamat: a kamat jóváírása havonta egyszer történik, a hónap végén. A kamatláb az egész évre érvényes kamatláb 1/12 részével egyezik meg.

Történelmi kapcsolódás: Manhattan „megvásárlása”

New York-i hagyományok szerint Manhattan-t 1626-ban a hollandok 60 guldenért (24 dollárnyi holland pénzért) vették meg az indiánoktól. (Valójában ez inkább területhasználati díjnak számított akkoriban. Az esetről Pieter Schaghen holland kereskedő számolt be a West India Company vezetőinek küldött, 1626. november 7-én kelt levelében.) Az indiánok egyik késői leszármazottja be akarta perelni az Egyesült Államokat, hogy milyen előnytelen üzletet kötöttek az őseivel, és kártérítést szeretett volna kapni. Azonban mielőtt a perre sor került volna, egy ügyvéd kiszámította, hogy nem az ár volt alacsony, hanem rosszul fektették be a vételárat: ha az 1626-ban kapott 24 dollárt akkoriban nagyon alacsonynak számító, mindössze 6%-os kamatra fektették volna be, akkor a közben eltelt 380 év alatt körülbelül 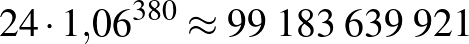$24\cdot 1{,}06^{380}\approx 99\;183\;639\;921$ dollárra növekedett volna az összeg, ami nem nevezhető alacsonynak.

Hitelkamatok összetétele

Mi határozza meg a banki hitelkamat mértékét?

$\bullet$ infláció: a kamatok jelenléte azt az általános várakozást eredményezi, hogy a jövőben mindenkinek több pénze lesz, így a növekvő pénzösszeggel együtt az árak emelkedése is közös társadalmi elvárás. Ez a növekedés az infláció, ami a pénz vásárlóértékének csökkenésével jár együtt. A pénzkölcsönzők semmiképpen sem akarnak kisebb vásárlóértékű pénzt visszakapni, mint amennyit kölcsön adtak, ezért általában a kamat az infláció feletti értéket vesz fel.

$\bullet$ nyereség: a pénzkölcsönző szervezet működési költsége

$\bullet$ kockázati felár: mennyire biztos a kölcsönző abban, hogy visszakapja a pénzét. A kockázati felár fedezi a vissza nem fizetett hitelekből származó veszteségeket is.

Nem egyidejű kifizetések: jelenérték

$\bullet$ Az inflációs hatás miatt a nem egyidőben történő kifizetések nominális értékének puszta összehasonlításával nem tudunk korrekt elszámolást végrehajtani. Nem mindegy, hogy egy adott pénzösszeg mikor kerül kifizetésre.

$\bullet$ Az összehasonlíthatóság alapja, hogy az összegeket „normáljuk”, egy adott, közös időpontbeli értékét vegyük figyelembe. Ezt az értéket hívjuk jelenértéknek. A jelenérték lehet természetesen jövőbeni időpontra számított is.

Példa egy elszámolásra a jelenértékszámítás alkalmazásával

A parlament eldönti 2018-ban, hogy 2021-re új kulturális központot építenek fel. Erre a célra 26 milliárd forintot szavaznak meg. A munkálatok elkezdődnek 2018-ban, és 2021-ben érnek véget.

A pénzek kifizetése a kivitelezőnek az alábbi ütemezésben történt:

2018-ban: 1 milliárd forint

2019-ben: 10 milliárd forint

2020-ban: 5 milliárd forint

2021-ben: 12 milliárd forint, ez így összesen 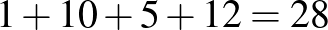$1+10+5+12=28$ milliárd forint

Az elszámolás alapja azonban nem lehet a konkrét kifizetett számlák összege, hiszen közben az infláció miatt emelkedtek az árak, és az esetleges túllépés nem jelenti azt, hogy a tervektől eltértek, de azt sem, hogy nem tértek el.

Megoldás. 2018-as árszínvonalon számítsuk ki az elköltött összeget

Az éves inflációt tekintsük az egyszerűség kedvéért 4%-nak.

a 2018-ra számított jelenértékek összege:

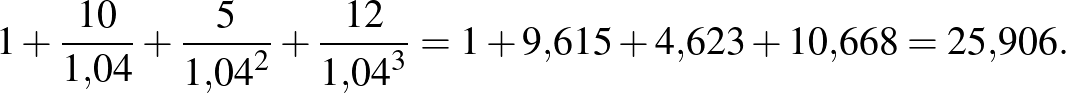
$\displaystyle 1+\frac{10}{1{,}04}+\frac{5}{{1{,}04}^{2}}+\frac{12}{{1{,}04}^{3}}=1+9{,}615+4{,}623+10{,}668=25{,}906.$

Ennek alapján a 2018-ban meghatározott költségvetési keretet az építkezés nem lépte túl.

Gyűjtőjáradék – Takarékoskodás folyamatos befizetésekkel

20 éven át minden év elején befizetünk a bankba 12 000 Ft-ot. A bank évi 6%-os kamatos kamatot ad a betétünkre. Hány forintunk lesz a 20 év elteltével a számlánkon?

Nézzük végig a folyamatot úgy, ahogy az időben zajlik. Ekkor az alábbi számítássort kapjuk a 20. év végén rendelkezésre álló összegre:

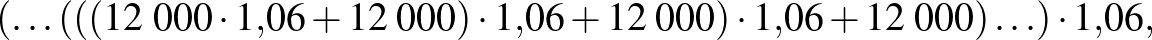
$\displaystyle (\ldots(((12\;000\cdot1{,}06+12\;000)\cdot1{,}06+12\;000)\cdot1{,}06+12\;000)\ldots)\cdot1{,}06,$

ahol az 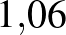$1{,}06$ -os szorzók száma 20 db (minden év végén hozzájön egy újabb szorzótényező).

A zárójeleket kifejtve a

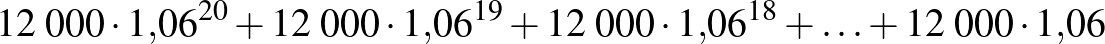
$\displaystyle 12\;000\cdot 1{,}06^{20}+12\;000\cdot 1{,}06^{19}+12\;000\cdot 1{,}06^{18}+\ldots+12\;000\cdot 1{,}06$

összeget kapjuk, amely egy mértani sorozat első 20 tagjának összege: a sorozat első tagja 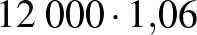$12\;000\cdot 1{,}06$ , hányadosa 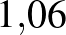$1{,}06$ . A keresett összeg:

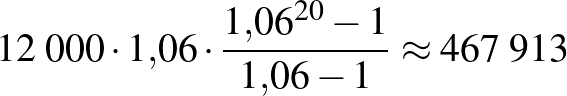$\displaystyle 12\;000\cdot 1{,}06\cdot \frac{1{,}06^{20}-1}{1{,}06-1}\approx 467\;913~$ Ft $\displaystyle .$

Megjegyzés: A

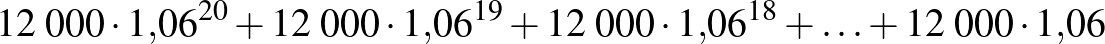
$\displaystyle 12\;000\cdot 1{,}06^{20}+12\;000\cdot 1{,}06^{19}+12\;000\cdot 1{,}06^{18}+\ldots+12\;000\cdot 1{,}06$

összeget megvizsgálva egy újabb értelmezést is felfedezhetünk: a betett pénzösszegeket egymástól elkülönülően kamatozó betétekként felfogva az egyes betétek kamatos kamatokkal növelt értékének összegét láthatjuk.

Gyűjtőjáradék típusú pénzgyűjtés folyik pl. a magán- és önkéntes nyugdíjpénztárakban, a befektetési életbiztosításokban, illetve a néhány éve bevezetett, állam által támogatott nyugdíjbiztosításokban.

A nyugdíjbiztosítás gyűjtőjáradék számítása hasonlóan történik, azonban annyi módosítással, hogy mivel a fizetésünket utólag kapjuk meg, ezért a befizetések nem az adott periódus elején, hanem a következő periódus elején (vagyis lényegében az aktuális periódus végén) zajlanak, így a kitevők 1-gyel elcsúsznak a fenti számításhoz képest (mert nem kamatozással, hanem befizetéssel ér véget a gyűjtő időszak).

Havi befizetések esetén a bank általában nem ad havi kamatos kamatot. Az általános eljárás az, hogy a befizetett összegekre 3 havonta írják jóvá a kamatot a gyűjtőszámlán, a biztosítók pedig éves szinten átlagosan megjelenő hozamot szoktak számítani, a hozam megállapításakor az egyes befizetések időpontját figyelembe véve.

Gyűjtőjáradékkal kapcsolatos feladattípusok

A gyűjtőjáradékkal kapcsolatban a következő feladatokat fogalmazhatjuk meg:

1. Évente adott összeget betéve a gyűjtőszámlánkra, adott idő elteltével mekkora lesz a gyűjtőszámlán levő összegünk?

2. Ha adott összeget szeretnénk elérni meghatározott idő elteltével, mekkora éves összegeket kell befizetnünk a számlánkra?

3. Hány év szükséges ahhoz, hogy adott összeget elérjünk, ha az évi befizetésünket meghatározott összegben tudjuk biztosítani (mert ez pl. a jövedelmünk függvénye)?

Az első két feladat egymással kompatibilis, az egyikkel elvégzett számításunk eredményét a másikra egy egyszerű arányossággal át tudjuk vinni.

Gyűjtőjáradék – annuitás, végösszeg kiszámítása

Kiszámítottuk korábban, hogy ha 20 éven át minden év elején befizetünk a bankba 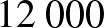$12\;000$ Ft-ot, és a bank évi 6%-os kamatos kamatot ad a betétünkre, akkor a 20 év elteltével a számlánkon

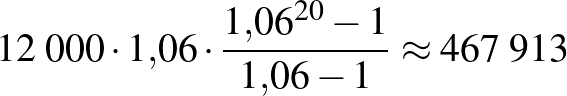$\displaystyle 12\;000\cdot 1{,}06\cdot \frac{1{,}06^{20}-1}{1{,}06-1}\approx 467\;913~$ Ft

lesz.

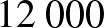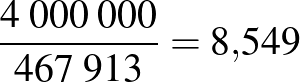Ha azt a kérdést tennénk fel, hogy évi hány Ft-ot kell befizetni, ha a célunk a 20 év elteltével 4 000 000 Ft elérése lenne, akkor könnyen látható, hogy a választ a $12\;000$ Ft $\frac{4\;000\;000}{467\;913}=8{,}549$ -szeresére növelésével tudjuk megadni, vagyis kerekítve évi 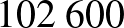$102\;600$ Ft lenne ehhez szükséges.

Járadékgyűjtés időtartamának kiszámítása

Ha a járadékgyűjtés időtartamát szeretnénk megtudni, akkor egy exponenciális egyenletet kell megoldanunk.

Hány éven át kell minden év elején 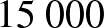$15\;000$ Ft-ot betennünk a bankba évi 6%-os kamatos kamatra, ha azt szeretnénk, hogy a folyamat végén (teljes éveket tekintve) 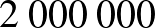$2\;000\;000$ Ft álljon a rendelkezésünkre?

Megoldás:

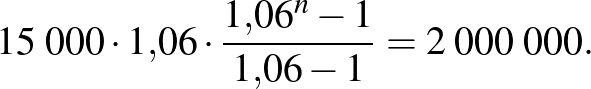
$\displaystyle 15\;000\cdot 1{,}06\cdot \frac{1{,}06^{n}-1}{1{,}06-1}=2\;000\;000.$

Az egyenletet rendezve

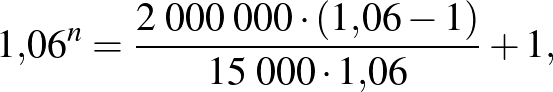
$\displaystyle 1{,}06^{n}=\frac{2\;000\;000\cdot (1{,}06-1)}{15\;000\cdot 1{,}06}+1,$

ahonnan

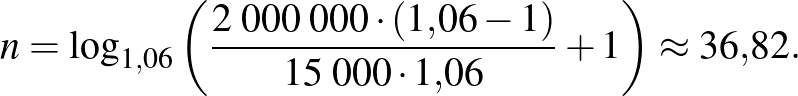
$\displaystyle n=\log_{1{,}06}\left( \frac{2\;000\;000\cdot (1{,}06-1)}{15\;000\cdot 1{,}06}+1 \right)\approx 36{,}82.$

Nyilván a feladat szempontjából a tört éveket nem tudjuk figyelembe venni, felfelé kell kerekítenünk, hiszen kamatfizetés csak év végén van. A kapott érték jelen esetben azt jelenti, hogy 36 év még kevés a célunk eléréséhez, 37 év elteltével pedig egy kicsit túl fogjuk lépni.

Járadékgyűjtés és infláció

Felmerülhet az a probléma, hogy a jelen számításokban nem vesszük figyelembe az inflációt. Az infláció hatására a befizetendő összegek megemelkednek, akár a nyugdíj-előtakarékosságot tekintve, hiszen a fizetésünk is emelkedik. Nézzük meg, mi történik, ha ezt is beépítjük a számításokba!

Tételezzük fel, hogy minden évben 3%-os az infláció. A bankba tett pénzünket tehát minden évben a korábbihoz képest 3%-kal növeljük. Ekkor az egyes befizetéseket a fentiekben megállapított módon önálló betétként kezelve az alábbi összeget kapjuk (a korábbi példában megadott kezdőösszeggel és kamattal számolva):

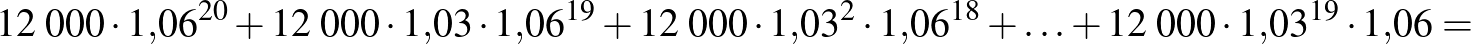
$\displaystyle 12\;000\cdot 1{,}06^{20}+12\;000\cdot 1{,}03\cdot 1{,}06^{19}+12\... ...cdot 1{,}03^{2}\cdot 1{,}06^{18}+\ldots+12\;000\cdot 1{,}03^{19}\cdot 1{,}06=$

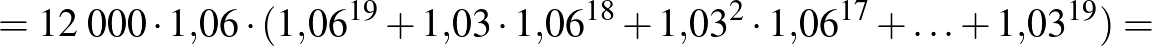
$\displaystyle =12\;000\cdot 1{,}06\cdot (1{,}06^{19}+1{,}03\cdot 1{,}06^{18}+1{,}03^{2}\cdot 1{,}06^{17}+\ldots+1{,}03^{19})=$

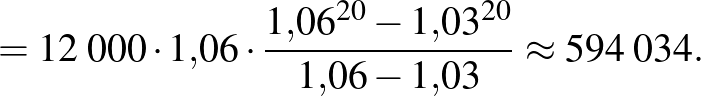
$\displaystyle =12\;000\cdot 1{,}06\cdot \frac{1{,}06^{20}-1{,}03^{20}}{1{,}06-1{,}03}\approx 594\;034.$

Az így kapott összeg az inflációval korrigált összeg, amelyre a jövőben számíthatunk. Ennek mai értékét azonban nehezen tudjuk felmérni, ezért jobb, ha inflációmentes számításokat végzünk. Ez lényegében a következőket jelenti: mai szinten ismerjük az árakat, a pénz értékét. A mai körülményekhez viszonyítva kapunk egy összeget, amely tekinthető alsó becslésnek a majdani kézhez kapott összeget tekintve (hiszen a befizetések nem fognak stagnálni).

Életjáradék – Az összegyűjtött pénz kifizetésének egy lehetséges módja

Beteszünk a bankba 4 000 000 Ft-ot, és szeretnénk minden év elején ebből ugyanakkora összegeket kapni 20 éven át. A bank a mindenkor bent lévő összegre évi 5%-os kamatos kamatot ad. Mekkora összeget tudunk kivenni minden év elején?

Legyen a keresett összeg 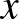$x$ . Ekkor a bankban levő pénzünk az alábbiak szerint alakul:

$\displaystyle (\ldots((((4\;000\;000-x)\cdot 1{,}05-x)\cdot 1{,}05-x)\cdot 1{,}05-x)\ldots)-x=0.$

A bal oldali képletben a kamatozást jelentő 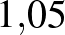$1{,}05$ -dal való szorzás 19-szer jelenik meg, hiszen az utolsó éves összeget a 20. év elején vesszük ki. Ekkor átalakítva az alábbi összefüggést kapjuk:

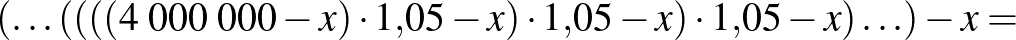
$\displaystyle (\ldots((((4\;000\;000-x)\cdot 1{,}05-x)\cdot 1{,}05-x)\cdot 1{,}05-x)\ldots)-x=$

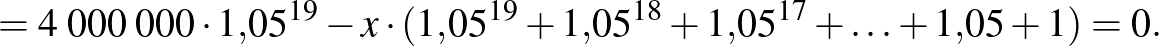
$\displaystyle =4\;000\;000\cdot1{,}05^{19}-x\cdot(1{,}05^{19}+1{,}05^{18}+1{,}05^{17}+\ldots+1{,}05+1)=0.$

Átrendezve:

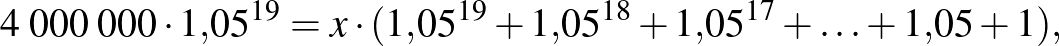
$\displaystyle 4\;000\;000\cdot 1{,}05^{19}=x\cdot (1{,}05^{19}+1{,}05^{18}+1{,}05^{17}+\ldots+1{,}05+1),$

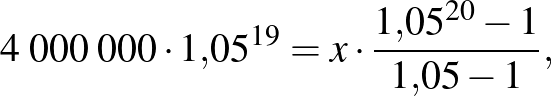
$\displaystyle 4\;000\;000\cdot 1{,}05^{19}=x\cdot \frac{1{,}05^{20}-1}{1{,}05-1},$

$\displaystyle x=\frac{4\;000\;000\cdot 1{,}05^{19}\cdot 0{,}05}{1{,}05^{20}-1}=305\;686.$

Tipikus folyamat, hogy először befizetünk egy adott pénzintézethez, biztosítóhoz aktív munkaképes időnk alatt, majd a befizetett és felhalmozott összeget járadék formájában kérjük kifizetni számunkra (pl. nyugdíjjáradék formájában).

2015 óta törvény rendelkezik arról, hogy életjáradékot csak biztosító vagy állami szervezet fizethet. Korábban volt olyan kezdeményezés, amelynek során lakásuk haszonélvezeti jogát megtartva, de tulajdonjogát átadva a nyugdíjasok cserébe életjáradékot kaphattak az erre szakosodott cégektől. Ma már ez nem lehetséges.

Nézzünk egy tipikus számítást nyugdíjalap-gyűjtésre, majd nyugdíjkifizetésre!

Gyűjtőjáradék és életjáradék kombinációja

Legyen egy fiatalember kellően tudatos, és 25 éves korában kezdje el fizetésének 10%-át gyűjteni. Alsó becslésként számoljunk a minimálbérrel mint fizetéssel, ez jelenleg kb. 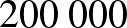$200\;000$ Ft, tehát 40 éven át havi 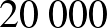$20\;000$ , azaz évi 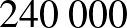$240\;000$ Ft-ot fizet be emberünk a biztosítóhoz, hogy majd nyugdíjat kapjon belőle. A hosszú távú befektetések kamatait vehetjük évi 5%-nak. Az egyszerűség kedvéért számoljunk éves betéttel és éves kamatjóváírással, mindig az év végén befizetve a pénzösszegeket.

A korábban már elemzett példa alapján a 40 év elteltével

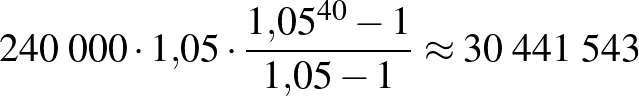$\displaystyle 240\;000\cdot 1{,}05\cdot \frac{1{,}05^{40}-1}{1{,}05-1}\approx 30\;441\;543~$ Ft

van a bankban.

Ezt a pénzt szeretnénk nyugdíj formájában megkapni, év elején felvéve az adott évre vonatkozó teljes összeget. A biztosító, tekintve, hogy a járadékfizetés alapját képző összeget már nem tudja hosszútávra befektetni, egy jelképes, 2%-os technikai kamattal számol a bentmaradó pénzünk gyarapodására. Itt azonban van egy kérdés, amit el kell döntenünk: fix időre szeretnénk járadékot kapni, vagy halálunkig, amely esetben a biztosító az átlagos várható élettartamunkra fog fizetni. Kérjük most 20 évre, optimista szemlélettel.

Ebben az esetben az előző példában elvégzett számítások alapján

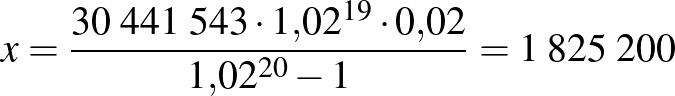
$\displaystyle x=\frac{30\;441\;543\cdot 1{,}02^{19}\cdot 0{,}02}{1{,}02^{20}-1}=1\;825\;200$

lesz az év elején felvehető összeg, tehát a havi összeg 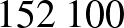$152\;100$ Ft, ami körülbelül annak felel meg, amennyit a bruttó 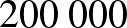$200\;000$ Ft-os fizetésünkből a kezünkhöz kapunk. Egy ilyen rendszerben tehát lényegében megállapítható, hogy 40 év alatt a mindenkori fizetésünk 10%-át befizetve a takarékoskodásra, a gyűjtőperiódus felének megfelelő időtartamra a korábbi jövedelmünket biztosítani tudjuk.

Felmerül itt az a kérdés, hogy ha halálunkig kérjük a járadék fizetését, akkor ezt a biztosító tudja-e fedezni. Ha a biztosítónak sok ügyfele van, akkor mindenki esetében az átlagos élettartamra számítva a járadékot, nagyjából az történik, hogy amennyivel előbb hal meg valaki az átlaghoz képest, egy másik valaki kb. annyival él tovább, tehát amit az egyiknek nem tudtak kifizetni a korai halála miatt, azt a másik ügyfél megkapja, és így kiegyensúlyozódik a dolog.

Van azonban itt egy momentum, amire kezdetben nem gondoltak: A kifizetések nem egyidejűleg történnek, hanem elcsúsztatva. Ha pl. átlagosan 10 éves élettartamra számolják a nyugdíjat, akkor ha valaki 5 év után meghal, a másik pedig 15 év után, akkor a korábban meghalt ember nyugdíját a túlélő csak 5 év eltolódással kapja meg. Ezalatt az 5 év alatt a bentmaradt összeg mindenképpen növekszik, azonban ezt a növekedést a járadékfizetés nem veszi figyelembe, hiszen a kiszámított fix összeget már 5 évvel korábban kifizették volna. Ez az extra haszon sok ügyfél esetén nem kis mértékű, de ma már törvény szabályozza, hogy ezt a biztosító nem nyelheti el, ki kell osztania az életben levő nyugdíjas biztosítottjai között.

Hiteltörlesztés – Hitelezés és a hitelek visszafizetése

A hitelfelvétel nyomán a keletkezett tartozásunk visszafizetése részletekben történik. Az a pénz, amivel tartozunk, az általunk befizetett összeggel csökken, így évről évre kevesebb lesz a tartozásunk. A kezdeti hitelösszeget természetesen minden esetben kamatokkal növelve tartják nyilván, tehát amikor részelszámolás történik, akkor mindig a korábbi tartozásunk kamatokkal növelt összegéhez képest csökken az aktuális tartozásunk.

Nézzünk egy példát!

Felvettünk 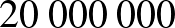$20\;000\;000$ Ft hitelt 20 évre, évi 7%-os kamatra. A törlesztés mindig az év végén történik, a kamatszámítás után, minden évben azonos összegekkel (ezt nevezzük annuitásnak). Mennyi legyen ez az összeg, hogy a hitelünk a 20 év alatt visszafizetésre kerüljön?

A tartozásunk az alábbi folyamatképlet szerint alakul:

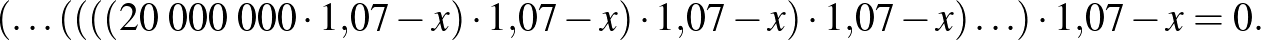
$\displaystyle (\ldots((((20\;000\;000\cdot1{,}07-x)\cdot1{,}07-x)\cdot1{,}07-x)\cdot1{,}07-x)\ldots)\cdot1{,}07-x=0.$

Az utolsó részlet befizetése a 20. év végén történik, előtte 20 kamatozás van. Az egyenletet rendezve és a mértani sorozat tagjaira vonatkozó összegképletet alkalmazva:

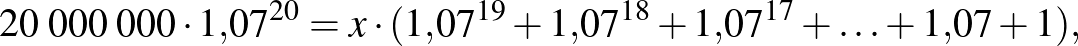
$\displaystyle 20\;000\;000\cdot 1{,}07^{20}=x\cdot (1{,}07^{19}+1{,}07^{18}+1{,}07^{17}+\ldots+1{,}07+1),$

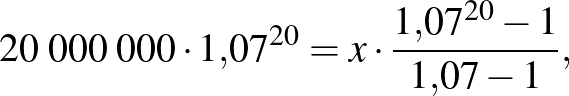
$\displaystyle 20\;000\;000\cdot 1{,}07^{20}=x\cdot \frac{1{,}07^{20}-1}{1{,}07-1},$

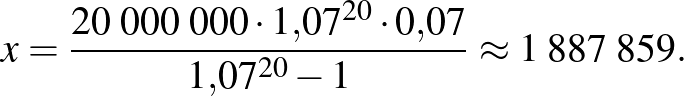
$\displaystyle x=\frac{20\;000\;000\cdot 1{,}07^{20}\cdot 0{,}07}{1{,}07^{20}-1}\approx 1\;887\;859.$

Láthatjuk, hogy ez a számítás nagyon hasonló az életjáradék-számításhoz, azonban annyi eltérés van, hogy itt előbb kamatozik az összeg, és csak utána csökkentjük, míg ott előbb csökkentettük, és csak utána kamatozott.

Miért annuitás, azaz miért fix összeg?

A bankok számára a legfontosabb dolog: szeretnék visszakapni a pénzüket. Az annuitás a hitel visszafizetésének egyik garanciája: ha kezdetben az adós ki tudja fizetni az adott törlesztőrészleteket, akkor ez később még inkább így lesz, hiszen a jövedelme emelkedik (infláció). Tehát az annuitás a bank számára biztonságot, az ügyfél számára pedig lényegében fokozatosan csökkenő terheket jelent.

A gyakorlat – Havi törlesztés

A gyakorlatban persze nagyon ritka az éves törlesztőrészletek fizetése, a gyakorlatban havonta fizetünk a banknak, és havonta el is számol velünk. Ez a fenti képletekre vonatkoztatva azt jelenti, hogy nem 20, hanem 240 kamatozás van, viszont egy alkalommal csak az éves kamatláb 1/12 részét fizetjük, jelen esetben 0,583% kamatot.

Végezzük el a havi törlesztőrészletre vonatkozó megfelelő számítást is:

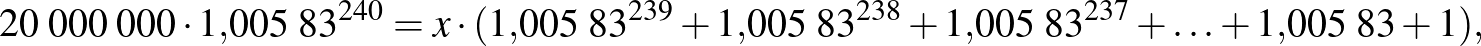
$\displaystyle 20\;000\;000\cdot 1{,}005\;83^{240}=x\cdot (1{,}005\;83^{239}+1{,}005\;83^{238}+1{,}005\;83^{237}+\ldots+1{,}005\;83+1),$

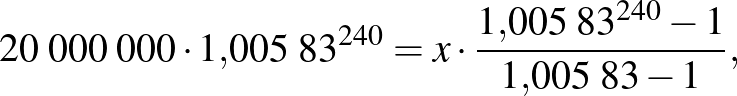
$\displaystyle 20\;000\;000\cdot 1{,}005\;83^{240}=x\cdot \frac{1{,}005\;83^{240}-1}{1{,}005\;83-1},$

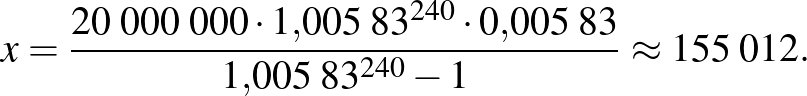
$\displaystyle x=\frac{20\;000\;000\cdot 1{,}005\;83^{240}\cdot 0{,}005\;83}{1{,}005\;83^{240}-1}\approx 155\;012.$

Az éves törlesztőrészletek esetén az egy hónapra jutó összeg: 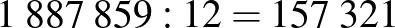$1\;887\;859:12=157\;321$ Ft. Miért magasabb ez az összeg, mint a havi fizetés esetén? Nyilvánvalóan azért, mert a havi törlesztéskor a kamatozó összeg (a tőke) azonnal csökken, így a törlesztés után már kisebb összeg után kell kamatot fizetnünk.

Ugyanakkor a havi kamatozás másik kérdést vet fel: havi tőkésítés esetén tulajdonképpen havi kamatos kamatszámítás történik, de mindez az éves kamatláb 1/12-ed részével, ami miatt az éves kamat tényleges értéke megváltozik.

Havi kamatos kamat éves viszonylatban

Számítsuk ki, hogy évi hány %-os kamatozásnak felel meg, ha havi 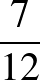$\frac{7}{12}$ % kamatot számolunk fel, havi tőkésítéssel!

Nyilvánvaló, hogy ha beteszünk egy tetszőleges összeget, akkor ez az éves kamatozás esetén az 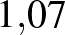$1{,}07$ -szorosára változik. Havi kamatos kamat esetén egy év elteltével

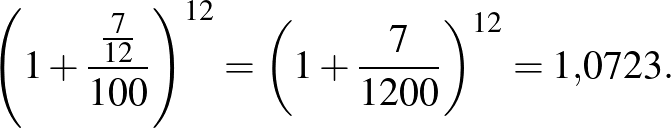
$\displaystyle \left( 1+\frac{\frac{7}{12}}{100} \right)^{12}=\left( 1+\frac{7}{1200} \right)^{12}=1{,}0723.$

Azt kaptuk tehát, hogy ez a számítási mód 7,23%-os kamatot jelent éves szinten.

Érdekes lenne tehát azt meghatározni, hogy az évi 7% kamatozásnak hány százalékos havi kamatos kamatozás felel meg.

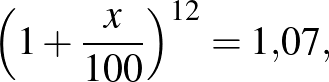
$\displaystyle \left({1+\frac{x}{100}}\right)^{12}=1{,}07,$

$\displaystyle x=100\cdot \left({\sqrt[{12}]{1{,}07}-1}\right)\approx 0{,}5654.$

Tehát havi 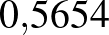$0{,}5654$ % kamatot kéne felszámítani, ami éves szintre lineárisan extrapolálva 6,78%-os kamatot jelent.

A bankok a hitelekre ezt a számítást az annuitás meghatározására használják, de a tényleges elszámolás ennél prózaibb módon történik. A hónap elején fennálló tőketartozás éves kamatát kiszámítják, ezt 360-nal osztják, majd megszorozzák az adott hónapban levő napok számával, így megkapják azt az összeget, amelyet az adós kamatként fog megfizetni az adott hónapra. A havi törlesztőrészlet fennmaradó összege a tőketartozást csökkenti.

Látszik, hogy ezzel a módszerrel februárban törlesztjük a legtöbbet a tőketartozásunkból, és a 31 napos hónapokban pedig a legkevesebbet.

Hány napból áll egy év? Rejtélyes módon a banki üzletszabályzatokban mindenhol 360 napnak tekintik az évet a napi kamat meghatározásakor, azonban a kamat tényleges kiszámításakor 365 napra számítják a kamatot. A korábbi havi kamatos kamat bevezetéssel a tényleges kamatláb így már gyakorlatilag a 7% helyetti 7,23%-ról 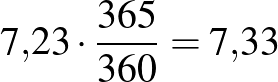$7{,}23\cdot \frac{365}{360}=7{,}33$ %-ra változik.

A bank nyeresége tehát kettős:

– Havi kamatos kamattal a kamatláb növelése.

– A napok számának egyoldalú csökkentésével a kamat növelése.

Kezelési költség

A korábbi hitelekben a bankok úgynevezett kezelési költséget is felszámoltak. A kezelési költség százalékos mértéke a hitel fennálló futamideje alatt változatlan volt, számítása az alábbiak szerint történt:

A naptári év elején fennálló tőketartozásra kiszámították a kezelési költséget egy éves időtartamra. Ezt az összeget elosztották 12-vel, és minden hónapban ezt a költséget fizette az adós, függetlenül attól, hogy a tőketartozása hónapról hónapra csökkent.

Tehát a törlesztőrészletből először a kamatot, aztán a kezelési költséget vonták le (utóbbit egy adott évben havi fix összegben), és a fennmaradó összeg ment a tőketartozás csökkentésére.

Jelenleg a kezelési költség és a fenti számítás létezik a banki üzletszabályzatokban, de a mértéke 0%.

A korábban kiszámított 20 éves futamidejű, 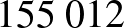$155\;012$ Ft havi törlesztőrészletű hitelünk nyomon követésével (például egy Excel-táblázatban) azt a meglepő eredményt kapjuk, hogy a 240 hónap elteltével még mindig 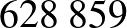$628\;859$ Ft tartozásunk van.

A havi törlesztőrészletet 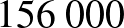$156\;000$ -re módosítva már csak 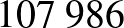$107\;986$ Ft a maradvány összeg.

Ezt a havi napi számítás, és a kerekítések együttesen okozzák. A korábban említett kamatemelő hatás miatt számoljuk újra a korábbi 7%-os kamatra felvett hitelünk havi törlesztőrészletét, most már 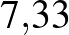$7{,}33$ %-os éves kamattal számolva!

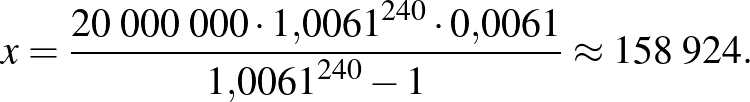
$\displaystyle x=\frac{20\;000\;000\cdot {1{,}0061}^{240}\cdot 0{,}0061}{{1{,}0061}^{240}-1}\approx 158\;924.$

Ezzel viszont már lényegében a 231. hónap végére elfogy a hitelünk, de mindenesetre ez jobb becslést ad a tényleges havi törlesztőrészlet értékére.

Végiggondolva a gyakorlati és az elméleti számítások közti eltérést (az Excel-táblázatban jelentkező szignifikáns maradványösszeg), arra a következtetésre juthatunk, hogy a havi kamatos kamat számítása nem okozhat problémát, hiszen a törlesztőrészeteket is havi kamatos kamat figyelembevételével számítottuk ki. Egyedül a bank által egyoldalúan alkalmazott, 360 napos évben 365 napra fizetett kamat kamatemelő hatása nincs beépítve a számításokba.

Számoljuk újra a korábbi 7%-os kamatra felvett hitelünk havi törlesztőrészletét, a 365 napra számolt 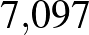$7{,}097$ %-os éves kamattal számolva!

Ennek havi kamatlába 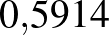$0{,}5914$ %. A módosított kamattal kiszámított havi törlesztőrészlet:

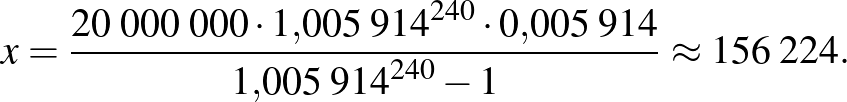
$\displaystyle x=\frac{20\;000\;000\cdot {1{,}005\;914}^{240}\cdot 0{,}005\;914}{{1{,}005\;914}^{240}-1}\approx 156\;224.$

Ezzel már lényegében rendben van, az Excel-táblázatban a 240. hónap végére kb. 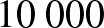$10\;000$ Ft túlfizetést kapunk, amit nyilván az utolsó törlesztőrészletben lehetne korrigálni.

A banki ajánlatokban láthatunk két olyan opciót, amely a kezdeti törlesztést könnyíti meg:

Csak kamat

A futamidő elején meghatározott ideig csak kamatot kell fizetni. Ez jelentősen alacsonyabb törlesztőrészletet eredményez, azonban ez egyben azt is jelenti, hogy a hitel tőketörlesztése ténylegesen nem kezdődik meg. A banknak ez a legjobb üzlet, hiszen így a tőketörlesztés hiánya miatt mindig megkapja a teljes kamatot. Ha ez így menne örökké, a bank vezetői fütyörészve hátradőlhetnének.

Csúsztatott hiteltörlesztés

A futamidő elején meghatározott ideig egyáltalán nem kell fizetni, a hitelösszegünk viszont rendes elszámolásban kamatozik. Ez a banknak szintén nagyon kedvező, mert így a kint levő hitelállományát anélkül növeli, hogy komolyabb erőfeszítéseket kéne tennie. A mi hiteltörlesztőrészletünk nagyobb lesz, vagy a futamidő hosszabbodik – mi mindenképpen rosszabbul járunk.

Magyar Zsolt
Szent István Gimnázium, Budapest