EGMO felkészülés: egy felépített feladatsor bemutatása
2022-ben, az Európai Lány Matematikai Diákolimpia kerek 10. évfordulóján Magyarország látja vendégül a kontinensről, sőt az összes földrészről érkező lánycsapatok delegációit Egerben.

Miért is jött létre ez a rendezvény? Azzal a szándékkal indult az EGMO, hogy bátorítást adjon a lányoknak matematikai tehetségük kibontakoztatásában − ami sokszor a környezeti hatások és a hagyományos társadalmi szokások, elvárások miatt nehézségekbe ütközik. Szeretnénk, ha ma, a 21. században egy matematikát sikerrel és örömmel művelő lány nem meglepő és furcsa, hanem természetes vagy akár trendi lenne. A magyarországi minta azt mutatja, hogy 10 év arra mindenképpen elég, hogy a felkészítő program hatására az váljon tipikussá, hogy az IMO+MEMO csapatban mindkét nem képviselve van − ez korábban nem így volt. Ez persze csak a jéghegy csúcsa, de visszahathat a tanárok és a jobb képességű diákok értékelésére is, szélesebb körű hatást kiváltva.
Mire helyezzük a hangsúlyt a felkészítésnél? Jelenleg két szálon zajlik a felkészülés. Egy, az elmúlt évtizedben kidolgozott forma az egyénre szabott képzést helyezi előtérbe, hangsúlyosan a versenyre készít fel. Ehhez kapcsolódóan az Érintő olvasóival már megosztotta gondolatait Fekete Panna és Kiss Melinda, korábbi EGMO olimpikonok, a közelmúlt csapatvezetői. Az EGMO-szervezéssel párhuzamosan indult egy közösségi, minitáborozós formájú képzés is − erről egy másik számban lehetett olvasni, Baran Zsuzsa és Molnár-Sáska Gábor tollából. Mindenki egyéni úton, a saját ritmusában tud egy-egy témakört elsajátítani. Ezért jellemzően tematikus feladatsorokat készítettünk, ahol a könnyebb, egyszerűbb gondolatokat igénylő feladatoktól a nehezebbekig úgy lehet eljutni, hogy a korábban megismert eljárásokat és ötleteket magasabb szinten újra hasznosítjuk. (A nemzetközi felkészítésben egyébként ez a mód nem új, sok helyen jelen van, és a felfedeztető matematikaoktatás is hasonló elven alapszik.) Elvárjuk, hogy a megoldásokat gondosan leírva kapjuk meg: az olimpiáig ki kell alakulnia annak a rutinnak, hogy hogyan kell egy megoldást bemutatni, milyen lépések egzakt leírása elengedhetetlen a teljes gondolatmenethez és a pontok begyűjtéséhez. Bár az alább bemutatandó feladatsort tábori környezetbe vittem, csapatmunkára; általában a felkészülés még jobban sikerül, ha több az idő, és az elakadásoknál személyre szabottan tudunk minden diáknak segíteni. Ez rendszerint azt jelenti, hogy elektronikus levélben kapják meg a diákok a feladatokat, és ugyancsak emailben válaszolnak, kérnek és kapnak segítséget, majd feltöltik a megosztani kívánt eredményeiket.
Jelen cikkünk célja egy ilyen tematikus feladatsor bemutatása. Javasoljuk először a feladatokkal való ismerkedést és a megoldások keresését, és csak ezt követően érdemes áttekinteni a kattintásra el(ő)tűnő megoldásvázlatokat és az ahhoz fűzött megjegyzéseket, reflexiókat. Minthogy a táborban a feladatsornak nem jutottunk a végére, az itt leírtakat a versenyre készülők külön levélben is megkapták.
Bevezető – Invariáns módszer és állapotfüggvények
Kicsi korunktól fogva észleljük, hogy a minket körülvevő világ tele van változásokkal, ugyanakkor a változásokat valamiféle rend, szabályosság jellemzi. A hétköznapi mintákon túlmutatva néhány kimondottan matematikai alapú példát jeleznék itt: a hold megvilágított, látható fele kiterjedésének növekedése és csökkenése, vagy egy feldobott labda mozgásának változása. Egy ettől eltérő jellegű jelenség, hogy bizonyos összebogozódó fonalak szépen kioldhatóak, másoknál meg a csomó feloldhatatlannak bizonyul, vagyis nem vihetjük át egyik állapotból a másikba. Ilyesmivel egyszerű kirakójátékoknál is találkozhatunk, mint a 15-ös (Sam Loyd-féle) kirakó: a lapocskák tologatásával nem juthatunk el a kezdőállapotból (amikor sorban következnek egymás után a számok) minden helyzetbe. (1. ábra)


1. ábra. A 15-ös kirakó, valamint egy nem-ekvivalens csomópár: balra a triviális (csomó nélküli) csomó, középen és jobbra az egyik csomótípus és átalakítása
Az első példapárban (hold, labda) közös, hogy a mozgást megfigyeljük, és a megfelelő modellek ismeretében matematikailag könnyen egészben leírhatjuk és értelmezhetjük.
Ezzel szemben a második példapárban (kirakó, csomók) az a közös, hogy a mozgást mi magunk alakíthatjuk, de van egyfajta rejtett szabály, aminek alapján nem juthatunk valamely állapothalmazból egy másik állapothalmazba. Ám ez utóbbi is megfogható matematikai eszközök segítségével: található olyan mennyiség (állapotokhoz rendelhető függvényérték), amely nem változik (invariáns), vagy esetleg jól leírható módon, például monoton módon változik.
Az alábbi kis gyűjtés abban szeretne segíteni, hogy különféle környezetekben felismerjük azt kulcsmennyiséget, aminek a változását vagy változatlanságát érdemes észrevenni és kimutatni. A feladatok mellé rövid megoldásvázlatokat valamint reflexiókat teszek közzé. Ezek célja terjedelmi okokból inkább csak a lényeg megragadása, ugyanakkor remélhetőleg elegendő ahhoz is, hogy az Olvasó (esetleg kis gondolkozással) azt kiegészítse teljes megoldássá. Az egyszerűnek tűnő, tömör megoldások azonban ne tévesszenek meg senkit: minél előbbre haladunk, többé-kevésbé annál nehezebbek a feladatok, és megoldásukhoz komoly lényeglátás és jó ötletek szükségesek. Némi gyakorlással azonban rá lehet vezetni a diákokat, hogy milyen nyomon érdemes elindulni, és hogyan válasszunk úgy egy, a változást leíró mennyiséget, hogy az állandó maradjon, vagy éppenséggel monoton módon változzon.
Bemelegítés
1. A francia kártya 52 lapját képpel felfelé az asztalra helyezzük, egy sorba. Panka kiválaszt két szomszédos kártyát, és ha közülük a bal oldali képpel felfelé van, akkor mindkettőt megfordítja. Ezt a lépést ezután többször is megismétli. Igazoljuk, hogy az eljárás egy idő után véget ér, vagyis valamennyi (véges sok) lépés után nem talál majd a szabály szerint megfordítható párt!1
Megoldásvázlat
Megoldásvázlat. Nézzük ezt a megfeleltetést: jelölje a kártyasorozatot egy 52 hosszú 0/1 sorozat, amiben 0, illetve 1 áll a képpel lefelé, illetve felfelé fordított kártyáknak megfelően.
Így a fordítások folyamán a sorozatot jelző bináris szám (mint állapotfüggvény) szigorúan monoton módon csökken. Minthogy nem csökkenhet 0 alá, és legalább egyesével csökken, az eljárás véget ér.
Reflexió
Reflexió. Az imént látott megoldást nevezhetjük lényeglátónak, de célba lehet érni úgy is − ami tipikus megoldás volt a táborozók körében −, hogy a forgatás folyamatához rendelt mennyiség a felfelé fordított lapok száma (1-esek száma a megfeleltetésben), ami könnyen láthatóan nem növekedhet. Azt kell ezt követően belátni, hogy ez csak véges sokszor maradhat változatlan értékű. De ez sem nehéz: egy olyan fázisban, ahol ez a mennyiség változatlan értékű, tekinthetjük úgy, hogy a felfelé és lefelé fordított kártyákat nem megforgatjuk, hanem kicseréljük, és így a felfelé fordított kártya a sorozat vége felé vándorol. Minden ilyen vándorló kártya legfeljebb 51 lépést tehet meg így.
2. Zsuzsa felírja 1-től 10-ig a pozitív egészeket a táblára. Gábor kiválaszt a számok közül kettőt, letörli, majd a különbségüket (a különbségük abszolút értékét) írja fel helyette. Ezt ismétli, amíg a táblán már csak egyetlen szám marad. Mi lehet ez a szám?
Megoldásvázlat
Megoldásvázlat. Az első varázsmennyiségünk legyen a táblán szereplő számok összegének paritása. Világos, hogy ez változatlan (invariáns) mennyiség, kezdetben pedig páratlan, hiszen 55 az összeg.
Másik varázsmennyiségünk a számok maximuma. Ez a mennyiség nem tud növekedni a folyamat során.
Így az 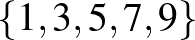 halmaz elemei jöhetnek csak szóba. Ezeket el is lehet érni.
halmaz elemei jöhetnek csak szóba. Ezeket el is lehet érni.
Reflexió
Reflexió. A paritás, vagy egy adott számmal vett maradék jellegzetes invariáns. Ezt jól magyarázza, hogy ha valamilyen műveletsor a vizsgált folyamat, akkor az adott művelethez kötődő ekvivalenciareláció fontos szerepet játszhat.
3. Anna és Bori a következő játékot játsszák. Először Borival együtt összes közös ismerősüket meghívják egy partira, így rajtuk kívül 2019 ember jelenik meg. Bori egy körbe rendezi a teljes társaságot, majd Annával felváltva lépnek. Minden lépésben a soron következő lány átküldi egyik szomszédját az ebédlőcsarnokba sütit enni. Anna kezd. Az nyer Anna és Bori közül, aki a másikukat el tudja küldeni. Kinek van nyerő stratégiája?
Megoldásvázlat
Megoldásvázlat. Annának lesz nyerő stratégiája. Az Anna és Bori közti két köríven összesen páratlan sok ember van, így az egyik íven páros, a másikon páratlan sokan lesznek. Ha Anna stratégiája az, hogy mindig a páros ívről küldi el a szomszédját, akkor Bori Anna minden lépése után mindkét irányban páratlan sok embert lát, és így bármelyik szomszédját küldi is el, az ismét páros-páratlan megosztást eredményez. Az emberek száma folyamatosan fogy; amikor a páros ívhez tartozó szám 0 lesz, Anna elküldi Borit, és nyer.
Reflexió
Reflexió. Matematikai stratégiai játékoknál nagyon gyakori, hogy a működő stratégia kulcsa valamilyen változatlan vagy jól kontrollálható módon változó mennyiség legyen. Itt most a páratlan emberből álló körívek száma volt a kulcsmennyiség.
4. Panna és Melinda egy 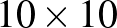 -es nagy csokitáblát kaptak a Bolyai Társulattól az EGMO csapat sikeres felkészítéséért. A következőt játsszák: felváltva kezükbe veszik a csokit, és a soron következő vagy egy törésvonal mentén az egyik darabot két részre töri, vagy a csokidarabok egyikét megeszi. Az a győztes, aki már nem tud sem törni, sem enni társa lépése után. Panna kezd. Kinek van nyerő stratégiája?
-es nagy csokitáblát kaptak a Bolyai Társulattól az EGMO csapat sikeres felkészítéséért. A következőt játsszák: felváltva kezükbe veszik a csokit, és a soron következő vagy egy törésvonal mentén az egyik darabot két részre töri, vagy a csokidarabok egyikét megeszi. Az a győztes, aki már nem tud sem törni, sem enni társa lépése után. Panna kezd. Kinek van nyerő stratégiája?
Megoldásvázlat
Megoldásvázlat. Minden lépés után a csokidarabok számának paritása változik, és kezdetben páratlan sok (egy) csokidarab van, míg a játék végén 0 csoki marad. Így mindenképpen a játékot kezdő Panna veszít. Panna vigaszdíja az lehet, hogy mivel így áll a dolog, az a legegyszerűbb, ha kapásból megeszi az egész táblát. J
5. Madagaszkár egyik erdejében kaméleonok élnek: ezek hangulatuktól függően meg tudják változtatni a színüket. David Attenborough megfigyelte, hogy 2020. július 9-én éppen 13 sárga, 15 szürke és 17 élénkzöld színű volt a kaméleonok között, valamint hogy amikor közülük két különböző színű találkozik, akkor mindkettő meglepetésében a harmadik színre vált át. Lehetséges-e, hogy a hónap folyamán
(a) mind azonos színre vált át?
(b) ugyanannyi lesz mindhárom színűből?2
Megoldásvázlat
Megoldásvázlat. Legyen 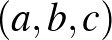 egy adott pillanatban a sárga, szürke, zöld kaméleonok száma. Ekkor egy találkozást követően kétféle színből eggyel-eggyel kevesebben, a harmadikból kettővel többen lesznek. A 3-mal való osztási maradékuk minden esetben
egy adott pillanatban a sárga, szürke, zöld kaméleonok száma. Ekkor egy találkozást követően kétféle színből eggyel-eggyel kevesebben, a harmadikból kettővel többen lesznek. A 3-mal való osztási maradékuk minden esetben 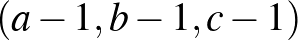 lesz
lesz 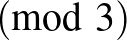 . Így ha az
. Így ha az 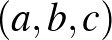 számhármasban mindhárom 3-as maradék előfordult kezdetben, akkor ez az idők végezetéig így marad. Tehát a válasz mindkét kérdésre nemleges.
számhármasban mindhárom 3-as maradék előfordult kezdetben, akkor ez az idők végezetéig így marad. Tehát a válasz mindkét kérdésre nemleges.
6. Egy 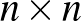 -es tábla mezőit kékre és pirosra színezzük, ahol
-es tábla mezőit kékre és pirosra színezzük, ahol 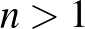 . Tudjuk, hogy a sarokmezők közül 3 kék és 1 piros. Igazoljuk, hogy vagy olyan
. Tudjuk, hogy a sarokmezők közül 3 kék és 1 piros. Igazoljuk, hogy vagy olyan 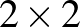 -es rész a táblán, amelyben a kék mezők száma páratlan.
-es rész a táblán, amelyben a kék mezők száma páratlan.
Megoldásvázlat
Megoldásvázlat. Összegezzük a kék mezők számát az összes 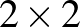 -es blokkban kétféle módon. (Kétszeres leszámolás.) Ha blokkonként nézzük, és az állítás nem volna igaz, akkor páros számot kapnánk. Vegyük azonban észre, hogy a sarokmezőket egyszer, minden más mezőt páros sokszor (kétszer vagy négyszer) számolunk az összegben. Így ellentmondást kapnánk, vagyis biztosan létezik olyan
-es blokkban kétféle módon. (Kétszeres leszámolás.) Ha blokkonként nézzük, és az állítás nem volna igaz, akkor páros számot kapnánk. Vegyük azonban észre, hogy a sarokmezőket egyszer, minden más mezőt páros sokszor (kétszer vagy négyszer) számolunk az összegben. Így ellentmondást kapnánk, vagyis biztosan létezik olyan 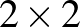 -es rész a táblán, amelyben a kék mezők száma páratlan.
-es rész a táblán, amelyben a kék mezők száma páratlan.
Reflexió
Reflexió. Miért invariáns jellegű ez a feladat? Mert egy jellegzetes, gyerekek által követett bizonyítási eljárás azon alapulna, hogy hogyan lehetne kiszínezni a táblát úgy, hogy csak páros számú kéket tartalmazó blokkot kapjunk. Ilyenkor az összes releváns színezés áttekintése helyett az az észrevétel jelent áttörést, hogy ha az egy híján csupa kék táblából indulunk, onnan vajon milyen tábla-színezések érhetők el. Kezdetben páratlan sok (1 db) „rossz” blokk van. Mivel a sarokmezőket nem színezzük át, minden egyes mező-átszínezés után teljesül, hogy a rossz blokkok paritása nem változik: ezt könnyű meggondolni. Eszerint a „rossz” blokkok száma sosem válhat nullává.
Gyorsítás
7. (a) Egy táborban 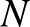 lány vesz részt. Sajnos a táborvezetőben az első nap tudatosul, hogy néhányan nemigen kedvelik egymást, de az szerencsére kiderül, hogy mindenki legfeljebb 3 másik résztvevővel van örök haragban. Biztosan két részre lehet-e a osztani a társaságot a számháborúhoz úgy, hogy mindkét csapaton belül mindenkinek legfeljebb egy örök haragosa legyen?
lány vesz részt. Sajnos a táborvezetőben az első nap tudatosul, hogy néhányan nemigen kedvelik egymást, de az szerencsére kiderül, hogy mindenki legfeljebb 3 másik résztvevővel van örök haragban. Biztosan két részre lehet-e a osztani a társaságot a számháborúhoz úgy, hogy mindkét csapaton belül mindenkinek legfeljebb egy örök haragosa legyen?
(b) Egy táborban 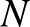 fiú vesz részt. Sajnos a táborvezetőben az első nap tudatosul, hogy néhányan eléggé tartanak a többiektől, de az szerencsére kiderül, hogy mindenki legfeljebb 3 másik résztvevőtől fél. Biztosan két részre lehet-e a osztani a társaságot a számháborúhoz úgy, hogy mindkét csapaton belül mindenki legfeljebb egyvalakitől tartson?
fiú vesz részt. Sajnos a táborvezetőben az első nap tudatosul, hogy néhányan eléggé tartanak a többiektől, de az szerencsére kiderül, hogy mindenki legfeljebb 3 másik résztvevőtől fél. Biztosan két részre lehet-e a osztani a társaságot a számháborúhoz úgy, hogy mindkét csapaton belül mindenki legfeljebb egyvalakitől tartson?
Megoldásvázlat
Megoldásvázlat. (a) Induljunk ki egy tetszőleges két csoportra bontásból, és nézzük a csoportokon belüli örökharag-kapcsolatok 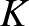 számát. Lokális javításokat alkalmazunk: ha találunk valakit, akinek minimum két ilyen kapcsolata van, akkor átrakjuk a másik csoportba. Ezt ismételgetve, az eljárás véges sok lépés után véget ér, mert a felosztástól függő
számát. Lokális javításokat alkalmazunk: ha találunk valakit, akinek minimum két ilyen kapcsolata van, akkor átrakjuk a másik csoportba. Ezt ismételgetve, az eljárás véges sok lépés után véget ér, mert a felosztástól függő 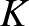 értéke mindig nemnegatív egész, és szigorúan monotonon csökken.
értéke mindig nemnegatív egész, és szigorúan monotonon csökken.
(b) 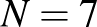 -re pl. könnyű látni, hogy nem mindig lehet. Jelölje nyíl a félelmek irányát a 2. ábra szerint, ahol az embereknek pontokat feleltetünk meg. Ebben a teljes irányított gráfban a kifokszámok (vagyis egy csúcsból kifele mutató nyilak száma, ami azt jelzi, kiktől fél az adott pontnak megfeleltetett fiú) értéke 3, ráadásul minden párhoz egyetlen él tartozik, tehát minden párban egyvalaki fél a másiktól. Egy kettéosztásnál nyilvánvalóan az egyik társaság legalább 4 fős lesz. Az őket reprezentáló 4 vagy annál több csúcsú gráfban biztosan nem lehet csupa 1-es kifok, mert több él van, mint csúcs.
-re pl. könnyű látni, hogy nem mindig lehet. Jelölje nyíl a félelmek irányát a 2. ábra szerint, ahol az embereknek pontokat feleltetünk meg. Ebben a teljes irányított gráfban a kifokszámok (vagyis egy csúcsból kifele mutató nyilak száma, ami azt jelzi, kiktől fél az adott pontnak megfeleltetett fiú) értéke 3, ráadásul minden párhoz egyetlen él tartozik, tehát minden párban egyvalaki fél a másiktól. Egy kettéosztásnál nyilvánvalóan az egyik társaság legalább 4 fős lesz. Az őket reprezentáló 4 vagy annál több csúcsú gráfban biztosan nem lehet csupa 1-es kifok, mert több él van, mint csúcs.
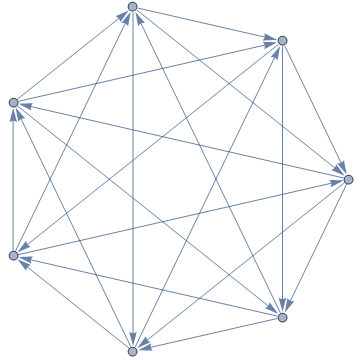
2. ábra. Irányított teljes gráf, minden csúcs kifoka 3
Reflexió
Reflexió. A vizsgált, ezúttal természetes mennyiség most nem volt invariáns, de biztosította az általunk mutatott kézenfekvő algoritmus végességét. Ilyen értelemben az 1. feladattal rokon probléma.
Ha akarjuk, javítások nélkül is elmondhatjuk ugyanezt: induljunk ki abból az elrendezésből, ahol a 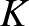 érték minimális. Ez épp azt jelenti majd, hogy senkinek nem lehet több haragosa a csoportjában.
érték minimális. Ez épp azt jelenti majd, hogy senkinek nem lehet több haragosa a csoportjában.
8. 12 lány kártyázik egy kerek asztal körül ülve. Kezdetben Lilinél van mind a 12 lap. Minden percben azok a lányok, akiknek legalább 2 lap van a kezükben, egyet-egyet a szomszédaiknak adnak. Hány perc múlva ér véget a játék?
Megoldásvázlat
Megoldásvázlat. Sosem ér véget. Nézzük ugyanis Lili lapjait. A körasztal Lilin átmenő szimmetriatengelyét figyelve azt látjuk, hogy Lili kezébe a két szomszédjától mindig egyszerre érkezik lap, vagyis a kezében levő lapok számának paritása nem változik.
Más megoldás: legyenek a játékosok körben  , és a kártyaelosztáshoz rendelt varázsfüggvény
, és a kártyaelosztáshoz rendelt varázsfüggvény 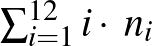 ahol
ahol 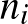 jelöli a kártyák számát
jelöli a kártyák számát 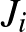 kezében. A varázsfüggvény változatlan
kezében. A varázsfüggvény változatlan  . De kezdetben és a végén különböző lenne, ha végül mindenkinél 1-1 kártya lenne.
. De kezdetben és a végén különböző lenne, ha végül mindenkinél 1-1 kártya lenne.
9. Legyen 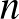 egy tetszőleges pozitív egész, és tekintsünk az
egy tetszőleges pozitív egész, és tekintsünk az 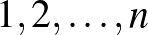 számok közül néhányat növekvő sorba rendezve. Minden lépésben kiválasztunk két számot ebből a listából, és kicseréljük őket. Lehetséges-e, hogy 2019 lépés után visszakapjuk az eredeti listát?
számok közül néhányat növekvő sorba rendezve. Minden lépésben kiválasztunk két számot ebből a listából, és kicseréljük őket. Lehetséges-e, hogy 2019 lépés után visszakapjuk az eredeti listát?
Megoldásvázlat
Megoldásvázlat. Nem lehetséges. Egy számpárt megfelelően rendezettnek mondunk, ha közülük a kisebb megelőzi a nagyobbat. Jelölje  azt a sorrendekhez rendelt számot, ami a nem megfelelően rendezett párok számát adja meg. (Ez az ún. inverziószám). Ha két számot,
azt a sorrendekhez rendelt számot, ami a nem megfelelően rendezett párok számát adja meg. (Ez az ún. inverziószám). Ha két számot, 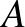 -t és
-t és 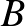 -t kicserélünk, amelyeknek a sorrendbeli távolsága
-t kicserélünk, amelyeknek a sorrendbeli távolsága 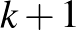 (vagyis
(vagyis  szám van köztük), akkor pontosan
szám van köztük), akkor pontosan 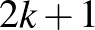 olyan számpár van, amelynek változott a helyzete a cserével. (Ti. az
olyan számpár van, amelynek változott a helyzete a cserével. (Ti. az 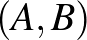 pár, valamint minden olyan pár, amelynek egyik eleme
pár, valamint minden olyan pár, amelynek egyik eleme 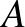 vagy
vagy 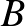 , a másik eleme pedig egy köztük helyet foglaló szám.) Így az inverziószám paritása páratlan sok lépés után csakis páratlan lehet.
, a másik eleme pedig egy köztük helyet foglaló szám.) Így az inverziószám paritása páratlan sok lépés után csakis páratlan lehet.
Reflexió
Reflexió. A bevezetőben említett 15-ös kirakónak épp ugyanez az inverziószám volt a nyitja! (Gondoljuk meg, hogyan.)
10. 19 barát kötélhúzásban akarja az erejét összemérni. Az igazságosság kedvéért elhatározzák, hogy egyikük a bíró, és a többi 18 két kilencfős csoportot alkotva mérkőzik meg úgy, hogy minden csoportban ugyanannyi legyen a résztvevők súlya. (Tudjuk, hogy mindegyikük súlya 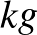 -ban egész szám.) Tegyük fel, hogy akárki is legyen a bíró, ezt az igazságos kettéosztást végre tudják hajtani. Igazoljuk, hogy ekkor mindegyikük egyforma nehéz.
-ban egész szám.) Tegyük fel, hogy akárki is legyen a bíró, ezt az igazságos kettéosztást végre tudják hajtani. Igazoljuk, hogy ekkor mindegyikük egyforma nehéz.
Megoldásvázlat
Megoldásvázlat. Jelöljük 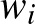 -vel az
-vel az 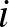 -edik ember súlyát. Ha a súlyösszeg
-edik ember súlyát. Ha a súlyösszeg 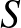 , akkor
, akkor 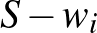 minden
minden 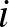 -re páros egész, vagyis minden
-re páros egész, vagyis minden 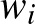 vagy páros vagy mind páratlan. Egységesen csökkentünk minden súlyt: vagy egy kilóval kevesebbre vagy a felére aszerint, hogy
vagy páros vagy mind páratlan. Egységesen csökkentünk minden súlyt: vagy egy kilóval kevesebbre vagy a felére aszerint, hogy 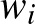 -k páratlanok vagy párosok. Akármelyik lépést hajtjuk végre, a keletkező súly-sorozatra is működni fog a feladat szerinti kettéosztási feltétel. Lehet-e, hogy az ilyen csökkentő és felező lépések sorozatát végtelen sokszor tudjuk megtenni?
-k páratlanok vagy párosok. Akármelyik lépést hajtjuk végre, a keletkező súly-sorozatra is működni fog a feladat szerinti kettéosztási feltétel. Lehet-e, hogy az ilyen csökkentő és felező lépések sorozatát végtelen sokszor tudjuk megtenni?
Vegyük észre, hogy a válasz nem, amennyiben van különböző is a súlyok között. Különböző súlyok ugyanis az egységes csökkentési lépések bármelyike esetén különbözőek maradnak. A súlyösszeg viszont minden lépésben legalább 1-gyel csökken, és persze minden súly mindig nemnegatív marad. Így csak akkor nem jutunk ellentmondásra, ha mindenki egyforma súlyú.
Reflexió
Reflexió. A feladat megközelíthető a súlyok számértékeiben a 2 prímkitevőjének vizsgálatával is; így számelméleti jellege jobban kidomborodik. Az eljárás lényegében az indirekt módszer egy válfaja, az úgynevezett végtelen leszállás (descente infinie). A gyűjtésbe azért került bele, mert itt is egy mennyiség jól követhető változása volt a megoldás kulcsa. A feladat nehézségét az (is) adja, hogy most nem csak a mennyiségre kellett rájönnünk, hanem a súlyokon végzett mozgásra is (egységes csökkentés).
Érdemes meggondolni, mennyiben változik a gondolatmenet, ha nem egész, hanem racionális súlyokkal vizsgáljuk a kérdést.
11. Van  darab számhalmazunk az
darab számhalmazunk az 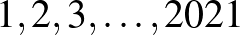 alaphalmazon. Ha találunk két metsző, de egymást nem tartalmazó halmazt,
alaphalmazon. Ha találunk két metsző, de egymást nem tartalmazó halmazt, 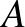 -t és
-t és 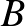 -t, akkor kicseréljük őket az uniójukra és metszetükre: az
-t, akkor kicseréljük őket az uniójukra és metszetükre: az 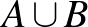 és az
és az 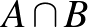 halmazokra. Igazoljuk, hogy az eljárás véges, vagyis egy idő után nem lesz metsző halmazpár.
halmazokra. Igazoljuk, hogy az eljárás véges, vagyis egy idő után nem lesz metsző halmazpár.
Megoldásvázlat
Megoldásvázlat. Gondoljuk meg, hogy a csere után a halmazok elemszámainak négyzetösszege szigorúan monoton módon növekszik. Véges sok  halmazból álló halmazcsaládunk van, és egyikhez sem juthatunk el kétszer, így az eljárás véget ér. (Ezt az eljárást, ahol két halmazt kicserélünk az uniójukra és a metszetükre, kikeresztezésnek is nevezik.)
halmazból álló halmazcsaládunk van, és egyikhez sem juthatunk el kétszer, így az eljárás véget ér. (Ezt az eljárást, ahol két halmazt kicserélünk az uniójukra és a metszetükre, kikeresztezésnek is nevezik.)
Reflexió. Miért pont a négyzetösszeget választottuk kulcsmennyiségnek, hogyan lehet erre rájönni? Igazából szabadon választhattunk volna mást is, és ez egy kényelmes választás volt. Olyan f egyváltozós függvényt szerettünk volna, amelyre Reflexió
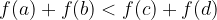 minden
minden 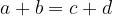 esetén, ahol
esetén, ahol 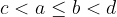 . Ez garantálja, hogy ha az f függvényt alkalmazzuk a halmazok méreteire és azt összegezzük, az eredmény szigorúan monotonon nő a cserék folyamán.
. Ez garantálja, hogy ha az f függvényt alkalmazzuk a halmazok méreteire és azt összegezzük, az eredmény szigorúan monotonon nő a cserék folyamán.
12. A valós számnégyeseken értelmezzük a következő műveletet:
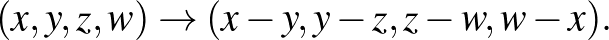
Lássuk be, hogy a műveletet elég sokszor végrehajtva, vagy 0-t kapunk az egyik koordinátában, vagy pedig egy 2020-nál nagyobb számot.
Megoldásvázlat
Megoldásvázlat. Világos, hogy az első lépéstől kezdve a számnégyesben az összeg zérus. Nézzük a négyzetösszeg változását! Azt állítjuk, hogy ez mindig legalább duplázódik. Valóban, ha egy nulla összegű 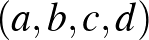 -ből indulunk, akkor
-ből indulunk, akkor

hiszen 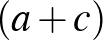 , illetve
, illetve 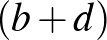 előjele zérus összegük miatt különböző. Innen lényegében kész vagyunk: ha az első lépés után a négyzetösszeg 0-nál nagyobb, akkor kellően sok lépés után a négy szám négyzetösszege nagyobb mint
előjele zérus összegük miatt különböző. Innen lényegében kész vagyunk: ha az első lépés után a négyzetösszeg 0-nál nagyobb, akkor kellően sok lépés után a négy szám négyzetösszege nagyobb mint 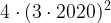 . De akkor van egy szám, aminek abszolút értéke több mint 6060. Ha pozitív, készen vagyunk, ha negatív, akkor a maradék 3 szám között van elegendően nagy pozitív a zérusösszeg miatt.
. De akkor van egy szám, aminek abszolút értéke több mint 6060. Ha pozitív, készen vagyunk, ha negatív, akkor a maradék 3 szám között van elegendően nagy pozitív a zérusösszeg miatt.
Reflexió
Reflexió. Ismét a négyzetösszeg (vagy általában a hatványösszegek) bizonyultak hatékony mennyiségnek!
Csúcshódítás
13. Adott 2017 egyenes a síkon, amelyek közül semelyik háromnak nincsen közös metszéspontja. Turbó, a csiga az egyenesek közül az egyiknek valamely pontjából elindul, és ezen egyenesek mentén halad a következőképpen: addig csúszik egy egyenesen, amíg el nem érkezik az egyenes és egy másik egyenes metszéspontjába. A metszéspontban a másik egyenesen folytatja útját, mégpedig úgy, hogy felváltva kanyarodik jobbra és balra az általa elért metszéspontokban. Irányt csak metszéspontokban válthat. Lehetséges-e, hogy egy útszakaszon mind a két irányban végighalad mozgása során? (EGMO 2017/3)
Megoldásvázlat
Megoldásvázlat. Indukcióval könnyű látni, hogy az egyenesek által határolt tartományokat két színnel (piros-zöld) színezhetjük ki úgy, hogy szomszédos tartományok színe különböző legyen.
Tegyük fel, hogy Turbó az egyik egyenesen úgy halad, hogy a szomszédos zöld tartomány oldalán az óramutató járása szerinti irányban mozog. Azt kell látni, hogy ez a mozgása során megmaradó tulajdonság: mindig egy olyan szakaszon mozog, aminek egyik oldalán a tartomány zöld, és mindig óramutató járása szerinti irányban mozog ennek a tartománynak a peremén. Ezt a feltétel biztosítja. Eszerint ugyanazon a szakaszon nem haladhat mindkét irányban.
14. A Margitsziget nagyrétjét 44 fa szegélyezi, és mindegyiken él egy izgő-mozgó mókus. Ezek közül kettő minden percben átugrik valamelyik szomszédos fára; egyik óramutató járása szerinti, másik azzal ellentétes irányba. Lehetséges-e, hogy a lakóhelyeikről indulva, egy idő után mindannyian ugyanazon a fán kötnek ki?
Megoldásvázlat
Megoldásvázlat. Tekintsük ismét azt az állapotfüggvényt, mint a 8. feladat második megoldásában, értelemszerűen most 44-es maradékok szerint: 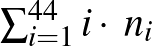 ahol
ahol 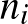 jelöli a mókusok számát a kör
jelöli a mókusok számát a kör 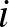 . fáján. Az összeg maradéka változatlan lesz, így nem juthat el minden mókus ugyanarra a fára.
. fáján. Az összeg maradéka változatlan lesz, így nem juthat el minden mókus ugyanarra a fára.
Reflexió
Reflexió. A 8. feladathoz közölt másik megoldás most nem működik.
Vegyük észre, hogy ez a feladat lényegében általánosítja a 8. feladatot, hiszen míg ott két irányba lehetett lépni a kör azonos pontjáról, most csak azt a feltételt tartottuk meg, hogy minden pillanatban mindkét irányba történik lépés, a közös indulási pont nem feltétel.
15. (a) Igazold, hogy egy tetszőleges háromszög feldarabolható véges sok darabra egyenes vágásokkal úgy, hogy a részekből átforgatás után egy téglalapot kapunk.
(b) Igazold, hogy mindez nem tehető meg semelyik háromszöggel sem, ha a feldarabolás után csak eltolási transzformációt használhatunk.
Megoldásvázlat
Megoldásvázlat. (a) Egy háromszögön belülre eső magasságvonal és a rá merőleges középvonal segíteni fog.
(b) Képzeljük el, hogy ez megvalósítható. Minden keletkező kis rész határát ceruzával rajzoljuk körbe az óramutató járása szerint a háromszögön belül, majd tegyük ezt a téglalapon belüli elrendezésben is. Utóbbi esetében azt látjuk, hogy tetszőleges egyenes által kijelölt meredekség esetén ugyanannyit haladtunk pozitív, mint negatív irányban: a téglalapon belül ez az eltolásból adódóan nyilvánvaló, és a határán is világos, hogy így van. A háromszögben azonban a három oldalegyenesnek megfelelő meredekségekre ez nem fog teljesülni.
16. Van 2020 piros és ugyanannyi kék pont a síkon, amelyek közül nincsen 3 egy egyenesen. Igazoljuk, hogy egyenes szakaszokkal összeköthetünk minden kék pontot egy pirossal úgy, hogy a szakaszok nem metszik egymást.
Megoldásvázlat
Megoldásvázlat. Egy másfajta kikeresztezést alkalmazunk. Kiindulunk egy tetszőleges piros-kék párosításból. Ebben még lehetnek metsző szakaszok. Ha találunk ilyen szakaszpárt, a piros pontokat a másik szakasz kék végpontjával kötjük össze. Ekkor a szakaszok összhossza mint állapotfüggvény csökkenést mutat, a háromszög-egyenlőtlenség szerint. Mivel véges sok összepárosításunk lehetséges, és minden állapotba legfeljebb egyszer jutunk, a javítási eljárás véges, vagyis lesz metszésmentes párosítás.
17. Adott egy  -es sakktábla. Erre szeretnénk minél több bábut felrakni a következő szabály szerint:
-es sakktábla. Erre szeretnénk minél több bábut felrakni a következő szabály szerint:
 bábuk csak mezők közepére kerülhetnek, minden mezőre legfeljebb egy,
bábuk csak mezők közepére kerülhetnek, minden mezőre legfeljebb egy,
 nem lehet élszomszédos mezőkön bábu,
nem lehet élszomszédos mezőkön bábu,
 bármely sorban vagy oszlopban szereplő hat szomszédos mező közül van két szomszédos, amelyen nem áll bábu.
bármely sorban vagy oszlopban szereplő hat szomszédos mező közül van két szomszédos, amelyen nem áll bábu.
Mennyi a bábuk maximális száma? (Latin-Amerikai Olimpia, 2004 nyomán)
Megoldásvázlat
Megoldásvázlat. Csúsztassunk végig a táblán egy 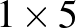 -ös dominót . Azt látjuk, hogy a dominó mindig legfeljebb 2 bábu helyét foglalhatja el: ha lenne valahol 3 vagy több, az sértené a fenti szabályt. Az egyik sarokmezőt levágva a táblát könnyű hézagmentesen egyszeresen lefedni ilyen dominókkal, tehát a válasz a skatulyaelv szerint legfeljebb
-ös dominót . Azt látjuk, hogy a dominó mindig legfeljebb 2 bábu helyét foglalhatja el: ha lenne valahol 3 vagy több, az sértené a fenti szabályt. Az egyik sarokmezőt levágva a táblát könnyű hézagmentesen egyszeresen lefedni ilyen dominókkal, tehát a válasz a skatulyaelv szerint legfeljebb 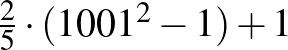 .
.
Ennyi azonban könnyen meg is valósítható. Alább a  -es táblának a képét mutatjuk, ahol a fekete mezőkre pakoljuk a bábukat, ennek kiterjesztésével kaphatjuk a bábupakolást a teljes táblára.
-es táblának a képét mutatjuk, ahol a fekete mezőkre pakoljuk a bábukat, ennek kiterjesztésével kaphatjuk a bábupakolást a teljes táblára.

3. ábra.
18. A szabályos ötszög csúcsaira egész számokat írunk, amelyek összege pozitív. Tegyük fel, hogy az ötszög mentén három szomszédos szám, 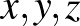 közül a középső negatív, azaz
közül a középső negatív, azaz 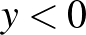 . Ekkor megengedett lépés, hogy az
. Ekkor megengedett lépés, hogy az 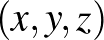 hármas helyére rendre az
hármas helyére rendre az 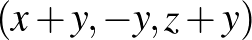 számokat írjuk be. Mutassuk meg, hogy ezt a lépést csak véges sokáig ismételgethetjük. (IMO 1986/3)
számokat írjuk be. Mutassuk meg, hogy ezt a lépést csak véges sokáig ismételgethetjük. (IMO 1986/3)
Megoldásvázlat
Megoldásvázlat. Két varázsváltozóval dolgozunk megint. Az első a számok összege, 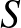 . Ez a lépések során világos, hogy változatlan.
. Ez a lépések során világos, hogy változatlan.
A másik változó legyen az oldalanként vett különbségek négyzetösszege, vagyis  esetén
esetén
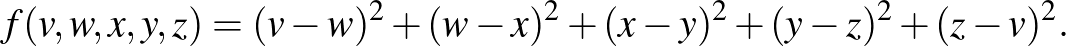
Ez egész szám, és igazolható, hogy a lépések folyamán folyamatosan csökken: a csúcsokra írt 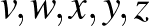 és
és 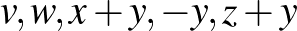 számötösökből képzett
számötösökből képzett 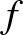 függvények különbsége
függvények különbsége 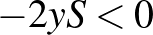 , ha
, ha 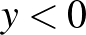 . Innen adódik az állítás.
. Innen adódik az állítás.
Reflexió
Reflexió. Az érdeklődőknek még ajánljuk Kós Géza 1987-es KöMaL-cikkét (538–560. o.) a probléma általánosításáról:
http://db.komal.hu/KomalHU/index.phtml
Természetesen más függvények is célhoz visznek, de a felépítés szerint a négyzetösszeg viszonylag természetes módon adja magát.
Felhasznált irodalom a feladatok egy részéhez
- [1] Arthur Engel: Problem-solving strategies, (Problem books in mathematics), 1997, Springer
- [2] Reiman István: Nemzetközi matematikai diákolimpiák 1959–1994, 1997, Typotex
- [3] Róka Sándor: 1500 Feladat az elemi matematika köréből, 1996, Typotex
- [4] Pablo Soberón: Problem-Solving Methods in Combinatorics – An Approach to Olympiad Problems, 2013, Birkhäuser Basel
Nagy Zoltán Lóránt,
EGMO csapatvezető 2014–18 és felkészítő, a 2022-es EGMO szervezői csapat tagja
Lábjegyzetek









