Bevezetés
Mit értünk (matematikai) analízis alatt?
A matematikai analízis (kalkulus) a matematikának egy részterülete, ami végtelen kicsi mennyiségekkel, vagyis infinitézimális számításokkal foglalkozik, azaz szorosan kapcsolódik a függvény, a határérték, a folytonosság, a differenciálhányados, az integrál, a sorozat, a végtelen sor fogalmához, a differenciálegyenletek, integrálegyenletek, függvényegyenletek, komplex függvények, funkcionálanalízis, variációszámítás, disztribúció-, potenciálelmélet, metrikus terek, mértékelmélet témakörökhöz.
A matematikai analízis fejlődésének főbb állomásai
A matematikai analízisnek (röviden analízisnek), mint tudománynak az eredete az ókorba nyúlik vissza, egészen Arkhimédészig (i.e. 3 sz.). Az infinitézimális számítás, vagyis a kalkulus megalkotói Newton és Leibniz voltak (17. század). Newton fizikai modellt használt (fluxióelmélet), Leibniz geometriai modellt választott, az érintő fogalmára alapozott. Problémát okozott, hogy nem voltak meg a pontos definíciók, hiányzott a határérték, az érintő pontos fogalma, de Leibniz gyakorlatilag nagyon ügyesen, sokszor analógiás alapon alkotta meg az eljárásait. Munkáikban sok volt a hiányosság, ezeket vette észre Euler. Euler három latin nyelvű könyvet írt analízisből. A Bevezetés a végtelenek analízisébe (1748) című kétkötetes művében felépítette a függvényelméletet. Tőle származik az 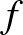 függvény
függvény 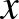 helyen vett helyettesítési értékének
helyen vett helyettesítési értékének 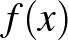 -szel való jelölése. Érdekes a tárgyalás módszere, mert minden definícióhoz ad konkrét példát. Van, amikor az általános fogalmat közli elsőként, de van, amikor a konkrét példa előzi meg az általános fogalmat. A második könyve a Differenciálszámítás alapjai (1755). Ebben kitért a függvények maximumának és minimumának megkeresésére. Nagyon sok kidolgozott példa található benne, olyanok, amelyek még ma is benne vannak a tankönyvekben és példatárakban. Ilyen pl. az
-szel való jelölése. Érdekes a tárgyalás módszere, mert minden definícióhoz ad konkrét példát. Van, amikor az általános fogalmat közli elsőként, de van, amikor a konkrét példa előzi meg az általános fogalmat. A második könyve a Differenciálszámítás alapjai (1755). Ebben kitért a függvények maximumának és minimumának megkeresésére. Nagyon sok kidolgozott példa található benne, olyanok, amelyek még ma is benne vannak a tankönyvekben és példatárakban. Ilyen pl. az 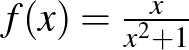 függvény vizsgálata, szélsőértékeinek megkeresése. Az integrálszámítás alapjai (1767–1770, 1794) háromkötetes könyvében először az alapokat tárgyalta. Megtaláljuk az integrálási szabályokat. Euler monográfiái összefoglalták a 18. századi matematikai felfedezéseket és azok gyakorlati alkalmazásait. Meghatározó szerepük volt a következő évszázadok tankönyveire és matematikai képzésére.
függvény vizsgálata, szélsőértékeinek megkeresése. Az integrálszámítás alapjai (1767–1770, 1794) háromkötetes könyvében először az alapokat tárgyalta. Megtaláljuk az integrálási szabályokat. Euler monográfiái összefoglalták a 18. századi matematikai felfedezéseket és azok gyakorlati alkalmazásait. Meghatározó szerepük volt a következő évszázadok tankönyveire és matematikai képzésére.
A határérték definíciója a geometriai fogalmaktól való elszakadás után, a 19. században Cauchy (1821) nevéhez fűződik, de ez sem volt pontos. Hiányzott hozzá még a valós és irracionális szám fogalmának axiomatikus értelmezése, amit Weierstrass (1815–1897) adott meg. A határozott integrál fogalmát Riemann (1854) pontosította. A fogalom továbbfejlesztése már a 20. századra esik és Lebesgue (1902) nevéhez fűződik, illetve összefügg a mérték fogalmával.
A matematikai analízis tanításának első állomásai
A matematikai analízis történeti fejlődése mutatja, hogy a matematika nehéz rész- területéről van szó. A tudományban is sok volt a tévút, a hiányosság. Lassan értek be a pontos fogalmak. Ezt nem szabad elfelejteni tanításakor. A fentiekből nyilvánvaló, hogy az analízis oktatása elsősorban a felsőfokú oktatás feladata és nagyon nehéz kérdés, hogy hogyan, milyen módszerrel vihető le a tudomány szintjéről a középfokú oktatás, illetve a felhasználást igénylő nem szakemberek szintjére. Ma is vannak kétségek, hogy kinek, mennyit, milyen mélységben tanítsunk, milyen módszerekkel kerüljön be a középiskolai matematikai oktatásba, hogyan lehet a modern informatikai eljárásokat alkalmazni a tanításában, mennyire kell az elméleti utat követni, mennyire kell csak a gyakorlati felhasználásra koncentrálni, van-e a középiskolai fizikatanításnak igénye rá?
Már a 19. században is voltak Magyarországon kísérletek az analízis tanítására. Bolyai Farkas a Tentamen-ben és a hozzá csatlakozó Errata-ban saját tudományos eredményeit szőtte be a diákok tananyagába (pl. konvergenciakritérium). A legfőbb problémát mégis az okozta, hogy nem volt meg a magyar szakmai műnyelv, ami a szakmai vonatkozások mellett újabb nehézséget jelentett. Bolyai Farkasnak (1775–1856) az analízisben használt új szavai meglehetősen bonyolultak voltak: differenciálás = külzés, limes = széj-becs, teorema = tét, geometriai sor = eggynézeti sor. Nagy Károly (1797–1868) könyveiben találjuk meg először a mai matematikai szaknyelvben is használt következő kifejezéseket, pl. szükséges és elég, nagyobb, mint akármely még oly nagy szám, csak egy és nem több.
Az ősi Debreceni Református Kollégium a 16. század óta élen járt a reáliák oktatásában. A felsőfokú képzéssel kapcsolatban a professzorok közül Kerekes Ferenc (1784–1850) nevét emeljük ki. Népszerű volt a diákok körében. Számunkra különösen érdekesek a tanítási módszerei, mert ő 1840-ben a heurisztikus tanítási módszer bevezetéséről írt. Analízissel kapcsolatos nézeteit a Csányi Dániel által kiadott A felsőbb mértan valódi alapelvei és egy toldalék töredékkel (Debrecen, 1862) könyvből ismerhetjük meg. A differenciál- és integrálszámítás témában Kerekes Euler nézeteit követte, de saját elképzeléseit is érvényesítette, amelyek ma nem egészen világosak már. Úgy gondolta, hogy különböző értékű zérusok vannak, de mi nem tudunk köztük különbséget tenni. Nézeteiből következtek a javasolt szakszavak: differenciálni = megnullítani, differenciálszámítás = nullító számvetés, differenciális calculus, leszálló nullszámvetés, integrálás = egészítés, integrálszámítás = egészítő számvetés, felhágó nullszámvetés. Érdemi eredményt nem ért el, mégis azt lehet mondani, hogy az Elmélkedés a Fellengős Mathesis igaz Sarkalatairól című, magyar nyelvű írásával elsőként vetette meg 1837-ben a differenciál- és integrálszámítás oktatásának hazai alapjait.
Kerekes véleményt mondott az axiomatikus tárgyalásról, nem tetszett neki, hogy Euklidész előre bocsátja a sok axiómát. Azt javasolta: „Ott hozzuk elő a definíciók, az axiómák, okoskodások mindegyikét, ahol először szükség van rá, vagyis hol a tudomány rendi szerint a sor reá kerül.”
A 19. század végére merült fel nemzetközi szinten a középiskolai matematikaoktatás megreformálása. Beke Manó Felix Klein mellett ismerkedett meg a matematikatanítási reformeszmékkel. Kezdeményezésére jött létre Magyarországon 1906-ban a Matematikai Reformbizottság, amelynek elnöke ő lett, titkára pedig az akadémikus fizikatanár Mikola Sándor. Mikola Sándort is foglalkoztatta a jövő középiskolájának a kérdése, ő elsősorban a fizika tanításának korszerűsítésével foglalkozott, de látta azt, hogy a fizikai fogalomalkotáshoz szükséges az analízis elemeinek az ismerete. A tagok között találjuk a Fasori Evangélikus Gimnázium híres matematikatanárát, Rátz Lászlót. A Reformbizottság fő feladatának a formális oktatás elleni harcot tekintette és a munkáltató matematikatanítás elvei alapján dolgozta ki a matematika tananyagát, tanítási módszereit, amit „A középiskolai matematika-tanítás reformja” című könyvükben fejtettek ki.
„Tanterveink mindinkább rendszerességre, a részek közti tervszerű kapcsolatra, koncentrációra törekszenek. Ezen kívül világos tendencia mutatkozik a matematikai tanítás gyakorlatias iránya felé, keresi a tanterv az élettel és a többi tantárggyal a kapcsolatot, tekintetbe veszi a gazdasági élet szempontjait, a szigorúan tudományos tanítás helyett, inkább egy-egy rész feldolgozásában nyújt a tanulóknak bepillantást a matematika tudományos problémáinak a tárgyalásába és e tekintetbe a függvények menetének vizsgálatában az összes külföldi tantervet megelőzi.”
A reform során előtérbe került a tanítás gyakorlatiasabbá tétele, a gyakorlat, a közvetlen tapasztalat és a becslés fontossága, a függvényfogalom, a differenciál- és integrálszámítás bevezetése, a sík- és térgeometria egységes tanítása, a geometria tanításának folytonossága, a térgeometriai rajzolás és modellezés.
A bizottság reális és szükséges reformokra törekedett. „El kell hagyni azokat a tárgyi dolgokat, amelyek idejüket múlták.” Kimondták, hogy redukcióra van szükség mind az algebra, mind a geometria tanításában. A fogalomalkotás viszont lassan és fokozatosan történjen meg.
Feladatok: a matematikaoktatás gyakorlativá tétele, a gazdasági érzék, a térszemlélet és a térbeli felfogó képesség fejlesztése, a mennyiségek viszonyainak grafikus ábrázolása, felhasználva hozzá a tanulók észleletgörbéit, az analitikai geometria tárgyalása, a függvényfogalom módszeres kiépítése, a differenciál- és integrálszámítás elemeinek bevezetése és felhasználása, legalább olyan mértékben, hogy a maximum-minimum feladatok, az egyszerűbb felület- és köbtartalom számítások általánosabb módon is elvégezhetők legyenek. (Jelentés a bizottság határozatairól és javaslatairól, 1909).
Beke Manót kérték fel az 1914. április 6–8. között Párizsban megrendezett Nemzetközi Matematikatanítási Kongresszus egyik főelőadójának, de Mikola Sándor is részt vett rajta. Témája annak a megvitatása volt, hogy a differenciál- és integrálszámítás bevezetésével milyen eredményeket értek el az egyes országok középiskoláinak felsőbb osztályaiban, illetve a főiskolákon. Ez utóbbi kérdés előadója Paul Stäckel heidelbergi professzor volt. A Matematikai Oktatás Nemzetközi Bizottsága Kérdőívet állított össze, ami a középiskolák felsőbb osztályaiban bevezetett differenciál-és integrálszámításra vonatkozott. A Bizottság azt akarta megtudni, hogy mit és hogyan tanítanak az egyes országokban. Az ismert volt, hogy a franciaországi líceumokban már 1902-ben bevezették, így célszerűnek látszott, hogy az előadó az egyes országok tapasztalatait összegezze, és az eredményeket összehasonlítsa. A Kérdőív kérdéseit megfelelő modernizálással ma is célszerű lenne elemezni, és az analízis tanítási céljait és módszereit újraértékelni.
Beke Manó elképzelése az analízis középiskolai tanításáról
Ma is szállóige Beke Manónak az a mondása, hogy magas szintű és korszerű középiskolai matematikaoktatást nem lehet a differenciál- és integrálszámítás bevezetése nélkül megvalósítani.
Beke tevékenysége arra az időszakra esett, amikor itthon is és nemzetközi viszonylatban is szóba került a középiskolai tananyag kibővítése a differenciál- és integrálszámítás elemeivel. Császár Ákos szerint: „ma sem tudjuk még igazában, hogy ezt hogyan lehet jól megcsinálni. De kísérletezni kell a megvalósításával”. Ez a 21. században is érvényes.
Beke Manó tankönyvei közül két könyvet emelünk ki, az ún. Kis Beke-ként emlegetett könyvét, vagyis a Bevezetés a differenciál- és integrálszámításba (1908) címűt, és a Nagy Bekét, vagyis kétkötetes Bevezetés a differenciál- és integrálszámításba (1910, 1916) egyetemi tankönyvét. Ezt a könyvet az egyetemi hallgatók nagyon szerették.
„Bekének a matematikusok között csak Kis Beke néven emlegetett Bevezetés a differenciál- és integrálszámításba című könyve mintaképe annak, hogy hogyan lehet szakmailag érdeklődő, de mégis nagyon kezdő fokon álló emberek számára érdekessé, népszerűvé tenni egy tudományt. A széles olvasóközönségnek szánta. Több kiadásban is megjelent és kiváló bevezetést nyújtott az analízis fogalmaiba és módszereibe. Érdekessége, hogy az 1960-as években, amikor ismét előtérbe került a differenciál- és integrálszámítás középiskolai bevezetése, a Gondolat Kiadó újból kiadta, ami nem véletlen, és amikor az ember újra előveszi, régi élmények jönnek vissza, hogy hogyan elevenedett meg annak idején és vált érdekessé, és érthetővé számára az analízis.” (Surányi János, 1987-es rádióriport)
„Az éppen most említett Kis Beke könyv, valóban a matematika népszerűsítésére szolgáló irodalomnak egyik gyöngyszeme, olyan elegánsan, olyan jól összeválogatott anyaggal ellátva, hogy ezt még ma is nagyon sok részletében minden változtatás nélkül fel lehet használni, akár egyetemi előadásokban is. Én magam is megteszem ezt egy-két, ebben a könyvben található példával, rendszeresen felhasználom őket.
Ami a nagy, kétkötetes differenciál- és integrálszámítás tankönyvet illeti, gazdag anyagot dolgoz fel, és imponáló a szerzőnek a korabeli irodalomban való tájékozottsága. Érdekes és sokoldalú képet nyújt az akkori kor analízisének az állásáról, és a Budapesti Egyetemen történő tárgyalásáról. Meg is írja az Előszóban, hogy úgy igyekezett a könyvet megírni, mintha egy egyetemi előadást jegyezne le, és ez valóban érződik, az olvasóban azt az érzést kelti, minthogyha egy egyetemi előadásnak volna a hallgatója éppen.” (Császár Ákos, 1987-es rádióriport)
Átnéztem a Nagy Beke könyvet. Természetesen azóta az analízis tudománya fejlődött, változott pl. a függvény, a függvények folytonosságának fogalma, egyes fogalmak neve, viszont a függvény határértékének fogalmát ma a tankönyvekben ugyanúgy szemléltetjük, mint ahogy ott van. Tapasztalatom szerint ez a szemléltetés érthetővé, világossá és megtanulhatóvá teszi a diákok előtt a kvantorok segítségével történő 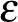 -os megfogalmazást.
-os megfogalmazást.
Beke Manó a Felix Klein által meghirdetett célokat akarta megvalósítani, ezek a matematikaoktatás közelebb hozása a társadalmi élethez, a természettudományos gondolkodás átvitele a köztudatba, a függvény fogalmának a bevezetése, a függvényközpontú gondolkodás, grafikus ábrázolás, grafikus táblázatok készítése, a differenciál- és integrálszámítás bevitele a középiskolába.
A Kis Beke a Népszerű Főiskolai Tanfolyam 1906. évi II. sorozatában tartott előadásokon alapult. Ebből szűrte le Beke Manó, hogy mit tart alkalmasnak középiskolai tárgyalásra. Rátz Lászlóval egyetértésben megállapíthatjuk, hogy ez a könyv nem középiskolás tankönyv, inkább a differenciál- és integrálszámítás alkalmazását igénylő szakemberek számára készült. A szemléletes tárgyalásra alapozott, nem igényelte a pontos matematikai fogalmak elsajátítását, inkább gyakorlati irányultságú. A másik nagy különbség az, hogy a fizikai alkalmazásokat akkor a matematika keretében tárgyalták. Ez mára már megváltozott. Nagyon kevés esetben azonos a matematika és a fizika tanára. Én még azok közé a tanárok közé tartoztam, akik ugyanabban az osztályban mindkét tárgyukat tanították. A speciális matematika tagozatos diákok viszont nem igényelték, hogy a matematikában megtanult integrálást alkalmazzuk a súlypont, a tehetetlenségi nyomaték, a hidrosztatika nyomóerő kiszámítására.
Beke Manóék célja az volt, hogy a tanároknak alkalmat adjanak a további elmélkedésre, de a végleges gyakorlati rögzítést nem tekintették feladatuknak. „Módszerünk mindenütt szemléletes és gyakorlati legyen. Tárgyalásunkban kerüljük a túlságos absztrakciót és a teljes precízióra törekvést, de itt-ott esetleg mutassunk rá azokra a kivételes viszonyokra, amelyek eljárásaink alkalmazhatóságának határt szabnak.”
Rátz László és Mikola Sándor elképzelése az analízis középiskolai tanításáról
A 20. század elején Rátz László is részt vett a magyar matematikatanítási reformmozgalomban. Kiemelt témával, a függvények, a differenciál- és integrálszámítás tanításával tankönyvíróként is, tanárként is foglalkozott fizikus kollégájával, Mikola Sándorral együtt. Tantervi átcsoportosításokat javasoltak, módszertani elképzeléseket fogalmaztak meg. Véleményük ma is időt álló és megfontolandó. Ők is a heurisztikus módszert tartották jónak. Rátz László Mikola Sándorral közösen írta meg A függvények és az infinitézimális számítás elemei középiskolában (1910, 1914) tankönyvet. A reformtörekvéseknek szellemében kidolgozott és már 1902-től bevezetett kísérleteknek megfelelő tanmenetek az 1924-es országos tanügyi reform során kerültek be a hivatalos gimnáziumi tantervbe, de közben egyes iskolák már hamarabb bevezették, pl. Budapesten Rátz László a Fasori Evangélikus Gimnáziumban, Debrecenben a Református Kollégium Gimnáziumában, a „nagy osztály” számára Jakucs István. Két diák nevét említem meg, akik ebből a könyvből sajátították el az analízis elemeit: a fasori Gimnáziumból Wigner Jenőét, Debrecenből pedig Bay Zoltánét, aki fél évszázaddal később is emlegette, hogy ebből az ügyes kis könyvből pompásan megértette és megtanulta az analízis alapjait.
A Kis Beke könyv és a Rátz–Mikola könyv az integrál fogalmának a bevezetésében különbözik, Beke a határozatlan integrállal kezd, míg Rátz–Mikola a határozott integrált tárgyalja előbb. Ez a kettős szemléletmód ma is nyomon követhető a tankönyvekben (pl. Czapáry Endre–Gyapjas Ferenc: Matematika, 11–12, Emelt szintű kiegészítő anyag (2008), Schlegl István–Trembeczki Csaba: Sokszínű Matematika, Az analízis elemei (2012)). Én a határozott integrállal való kezdést tartottam jobbnak és érthetőbbnek. Egyidőben tartottam az egyetemen analízis gyakorlatot elsőéves matematika szakos hallgatóknak, és tanítottam „specmatos” diákokat. Megpróbáltam nekik több ekvivalens definíciót adni az integrálra. Nem volt sikerem. Nem értették meg, hogy erre miért van szükség, pedig a későbbiekben az osztály minden tagja felsőfokú végzettséget szerzett, sőt nagyobbik fele matematikusként, vagy matematikatanárként végzett. Nekik könnyebbség volt az egyetemi tanulmányaik során, hogy ismerték az analízis alapvető fogalmait. Talán az volt a szerencséjük, hogy azonos stílusban sajátították el mind a középiskolai, mind az egyetemi analízis tananyagot.
Hozzám a két tárgyalásmód közül a Rátz–Mikoláé áll közelebb. Jónak tartottam a függvényvizsgálatnál követett táblázatos és szemléletes ábrázolási módot, én is ezt mutattam meg és vártam el tanítványaimtól, ma is ez szerepel a tankönyvekben. Sokat tanultam Urbán Jánostól a „specmatos” tanárok éves továbbképzésén az 1960-as évek második felében, amikor ismét előkerült az analízis bevezetése a középiskolákban. Rengeteg függvényt ábrázoltunk, határértéket kerestünk, folytonosságot, monotonitást vizsgáltunk, deriváltunk, integráltunk, sorba fejtettünk, tételeket fogalmaztunk meg, bizonyítottunk, foglalkoztunk a kivételekkel, (pl. ez a függvény alkalmas arra, hogy a folytonosság szemléletes képét megingassa), de előkerült a példa a mindenütt folytonos, de sehol sem differenciálható függvényre is.
A Rátz–Mikola könyvből válogattam a 11. évfolyamos diákok számára a 2013. évi Révkomáromi Nagy Károly Diáktalálkozóra egy 9 feladatból álló feladatlapot a függvények maximális és minimális értékeinek meghatározására. A Diáktalálkozón részt vevő középiskolás diákok emelt szinten tanulták a matematikát. Ismerték a differenciálhányados fogalmát és a közepek közti összefüggéseket is. A feladatok egy részét meg lehetett volna oldani elemi úton is, de ők a differenciálást választották.
Hasonló volt a tapasztalatom egy kooperatív tanulással kapcsolatos tanítási kísérletnél, amiben négy középiskola 9–11 évfolyamos tanulói vettek részt. A kitűzött feladat: Egy farmer 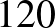 m hosszú drótkerítéssel akar körbe keríteni egy téglalap alakú füves legelőterületet. Határozzuk meg a körbe keríthető terület maximumát!
m hosszú drótkerítéssel akar körbe keríteni egy téglalap alakú füves legelőterületet. Határozzuk meg a körbe keríthető terület maximumát!
Azt tapasztaltuk, hogy a 9–10. évfolyamos diákok elemi úton oldották meg a feladatot, míg a 11. évfolyamon, a fakultatív oktatásban részt vevő tanulók a differenciálást választották, azzal a megjegyzéssel, hogy így könnyű a számítás.
Ugyanez volt a helyzet most, 2021-ben, a Református Iskolák Országos Versenyén is, ahol a 12. évfolyam 3. feladata másodfokú függvény maximumának a meghatározására vezetett. A 3. feladat a következő volt:
Legyen  az
az 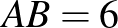 hosszúságú szakasz belső pontja. Az
hosszúságú szakasz belső pontja. Az 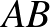 ,
, 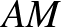 és
és 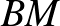 szakaszok mint átmérők felé félköröket írunk az
szakaszok mint átmérők felé félköröket írunk az 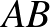 szakasznak ugyanarra a partjára. Hol helyezkedik el az az
szakasznak ugyanarra a partjára. Hol helyezkedik el az az  pont, amelyre a legnagyobb a három félkör által határolt síkrész területe? Adja meg a maximális síkrész területét!
pont, amelyre a legnagyobb a három félkör által határolt síkrész területe? Adja meg a maximális síkrész területét!
A megoldás során a 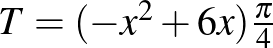 függvény maximumát kellett meghatározni. Itt is azt tapasztaltam a top 20 tanuló versenydolgozatának az átnézésekor, hogy főképpen differenciálással oldották és nem elemi úton.
függvény maximumát kellett meghatározni. Itt is azt tapasztaltam a top 20 tanuló versenydolgozatának az átnézésekor, hogy főképpen differenciálással oldották és nem elemi úton.
Következtetés: a matematikát emelt szinten tanuló tanulók szívesen és előszeretettel alkalmazzák a differenciálást, mint rutineljárást a szélsőérték meghatározására.
A 20. század eleji középiskolai tankönyvekben tárgyalt analízis anyag
1913-ban adták ki Borosay Dávid és Lévay Ede középiskolás tankönyveit. 1923-ban jelent meg Borosay Dávidnaka VI–VIII. osztályok számára készült tankönyve. Tárgyalta a függvény fogalmát, folytonosságát, ábrázolását, a másodfokú egész függvény maximumát és minimumát, a másodfokú egyenlet grafikus megoldását, a szinusz- és koszinuszfüggvény ábrázolását. Ennél a tárgyalásnál is az volt a probléma, hogy nem alakította ki a függvény határértékének a fogalmát, és a folytonosság szemléletes fogalma megelőzte a határértéket.
Tapasztalatom szerint a határérték fogalma nehezebb, mint a folytonosságé, vagy a differenciálhányadosé. Számomra egyetemi hallgatóként Rapcsák András akadémikus professzor tanította az elsőéves analízist. Még november elején is a nullsorozatoknál és a „hangyabokányi” 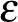 -nál tartottunk.
-nál tartottunk.
A középiskolák szerkezetét 1924-ben megváltoztatták. A matematika tananyag korszerűbb lett, de zsúfoltabb. Az időhiány miatt a kitűzött célok, pl. a tanulók önálló munkája, nem valósultak meg, megsokasodtak a problémák, a tanárok tiltakoztak. 1938-ban a Teleki-féle egységes középiskolai tanterv csökkentette az óraszámot, összevont anyagrészeket. Így egyre nagyobb problémává vált az analízis oktatása. Az 1943-as évben több fórum is jelezte ezt.
A református gimnáziumok Jónás Márton Mennyiségtan tankönyveit (1945) használták. Nála már a VI. osztályban a sorozatok tárgyalásakor, a végtelen geometria sornál megjelent a határérték, a konvergencia, a divergencia elnevezés, a fogalom pontos tárgyalása nélkül. Erre alapozta a VII. osztályban az 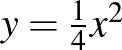 másodfokú racionális egész függvény differenciálhányadosának a meghatározását. A folytonos és nem folytonos függvény fogalmát is konkrét függvények ábrázolásával kötötte össze. Szó esett a fizikai alkalmazásokról is (sebesség, gyorsulás, harmonikus rezgőmozgás). Az integrál esetében ő is a határozatlan integrál bevezetésével kezdett. A VIII. osztályban, az első fejezetben, a Függvénytant átismételte. Kiemelném, hogy nagyon szépek az ábrák, rajzolói között neves művészek voltak: G. Szabó Kálmán festőművész-grafikus és Drahos István festőművész.
másodfokú racionális egész függvény differenciálhányadosának a meghatározását. A folytonos és nem folytonos függvény fogalmát is konkrét függvények ábrázolásával kötötte össze. Szó esett a fizikai alkalmazásokról is (sebesség, gyorsulás, harmonikus rezgőmozgás). Az integrál esetében ő is a határozatlan integrál bevezetésével kezdett. A VIII. osztályban, az első fejezetben, a Függvénytant átismételte. Kiemelném, hogy nagyon szépek az ábrák, rajzolói között neves művészek voltak: G. Szabó Kálmán festőművész-grafikus és Drahos István festőművész.
Az analízis középiskolai tanításának kritikái
A Mennyiségtani és Természettudományi Didaktikai Lapok (1943. I. évf. 5. szám) vita rovatában jelent meg Alexits György írása arról, hogy Tanítsuk-e az analízist a középiskolában? ([1]) A „szemlélet segít” csatakiáltás ellen lépett fel, azzal, hogy a középiskolai analízis tanításában hemzsegnek a hibák, ködös, vagy éppen hibás fogalmakkal, bizonyításokkal van tele. Szerinte a differenciálszámítás alapja a határérték fogalma, aminek kialakítása nem történik meg, még számsorozatok esetén sem. Nem világos a folytonos és a differenciálható függvények közti kapcsolat, nehezen érthető a szakadásos függvény fogalma. A szemléletesség kapcsán a bizonyítások csak olyan függvényekre érvényesek, amelyek lokálisan monotonok. Hibás az összetett függvény differenciálási szabálya, mert feltételek hiányoznak belőle, nem pontos a függvény fogalma sem, mert csak szemléletes. Azt tartotta, hogy a középiskolákban tanított infinitézimális számítás zavarosságának koronája a Riemann-integrál. Szerinte ez a fogalom nehéz, és igen finom meggondolást kíván. A középiskolában való tanításának már azért sincs semmi értelme, mert a Riemann-integrál igazi értéke csak akkor mutatkozik meg, ha olyan függvényekre kívánjuk kiterjeszteni az integrálhatóság fogalmát, amilyenekre a középiskolában még példát sem tudunk mondani. „Miért éppen a Riemann-féle és miért nem a Lebesgue-féle integrállal riasztjuk el a tanulókat a matematikai gondolkodástól? Az átlagos gimnazisták, pedig egy nullaméretű halmaztól eltekintve, Lebesgue-ül se tudnának rosszabbul integrálni, mint ahogy Riemann-ul tudnak.”
Nekem ezzel kapcsolatban egy érdekes tapasztalatom van. Az egyik „specmat”-os osztályomban tartottam országos bemutató órát, amelyen a síkbeli alakzatok területének meghatározásáról volt szó, kiegészítve azzal a kérdéssel, hogy létezik-e minden síkbeli alakzatnak/ponthalmaznak területe? A vizsgált halmazt a Dirichlet-függvény általánosításaként adtuk meg, vagyis az volt a kérdés, hogy van-e területe a derékszögű koordináta-rendszer azon pontjai halmazának, amelyeket úgy származtatunk a 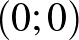 ,
, 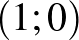 ,
, 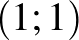 ,
, 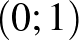 koordinátájú pontokkal határolt egységnégyzetből elhagyjuk (szemléletesen kiszúrjuk) azokat a pontokat, amelyeknek mindkét koordinátája racionális. Az egyik tanuló azt javasolta, hogy gurigázzuk össze ezeket a pontokat az origóba és akkor már meg tudjuk adni a területet. Véleménye a bemutató tanításon elnöklő Surányi János professzort is meglepte. Talán mégsem olyan rémisztő a diákok számára a Lebesgue-integrál fogalma?
koordinátájú pontokkal határolt egységnégyzetből elhagyjuk (szemléletesen kiszúrjuk) azokat a pontokat, amelyeknek mindkét koordinátája racionális. Az egyik tanuló azt javasolta, hogy gurigázzuk össze ezeket a pontokat az origóba és akkor már meg tudjuk adni a területet. Véleménye a bemutató tanításon elnöklő Surányi János professzort is meglepte. Talán mégsem olyan rémisztő a diákok számára a Lebesgue-integrál fogalma?
A probléma másban gyökerezett, a diákok azt fogták fel nehezen, hogy lényeges különbség van azon két állítás között, hogy pl. egy síkbeli ponthalmaznak nem létezik területe, vagy a terület mértéke 0. A másik nehézség a végtelen fogalmának tisztázása volt. Nem volt nyilvánvaló a számukra, hogy nemcsak egy fajta végtelen van. Értelmes diákoknak is hosszú idő kellett a megértéséhez.
Alexits György olyan tanulók számára tartotta reálisnak az analízis tanítását, akik a gimnáziumban matematika tagozatra járnak, és legalább heti 5-6 órában tanulják a matematikát. Ezzel nagyon egyet lehet érteni. A 20. század második felében, illetve a 21. században a megvalósítás reális útja is ez (matematika tagozat, speciális matematika tagozat, emelt szintű oktatás), sőt kiegészült az IKT-eszközök felhasználásával. Alexits György végső következtetése az volt, hogy ennek az állapotnak csak egy gyógyszere van: „Ne tanítsunk a mai gimnáziumban infinitézimális számítást!” Nincs a középiskolai fizikának erre feltétlen szüksége.
Tóth Ferenc: Mégiscsak tanítsunk infinitézimális számítást a középiskolában című cikkében vitába szállt Alexits Györggyel. Megállapította, hogy a hibák vonatkozásában Alexits Györgynek igaza van. „De, mert a tankönyveink rosszak, ez nem ok arra, hogy ne tanítsuk a középiskolában az infinitézimális számítást.” Barra György a Tanítsunk-e a középiskolában infintézimális számítást? című cikkében a tanárok hozzáállásáról mond negatív véleményt: „megfelelő előkészítés nélkül tanítanak egyes részleteket, elhanyagolnak fontos részleteket. Szükséges a tanár teljes biztonsága a szóban forgó ismeretkörben, és a helyes didaktika annak közlésében.” ([2])
A tankönyvi hibák megismétlődtek a későbbiekben, pl. amikor a tanterv a szakközépiskolákban meghagyta az analízis tanítását (Czapáry szakközépiskolai tankönyve), míg a gimnáziumokban „taníthatatlan anyag” címmel eltörölte. Egyoldalú és nem körültekintő szemléltetésből származó szakmai hibák voltak pl. Cser Andor tankönyvében az integrálszámításnál, ahol a szerző azt állította, hogy az integrálközelítő összegek szigorúan monotonok, ami természetesen csak az általa felvázolt szigorúan monoton függvényre teljesült.
Az analízis középiskolai tanításának új alapokra helyezése
Az 1940-es években is használt legjobb tankönyveket Veress Pál írta. Barra György A mennyiségtan tanítása c. szakmódszertani könyvében (1943) ezt a tankönyvsorozatot elemezte. ([3]) Megjelent benne a függvény folytonosságának fogalma, megemlítette a középértéktételt. Az integrál fogalmát ő is a differenciálás inverz műveleteként vezette be. A határozott integrál fogalmát a középértéktétel felhasználása miatt elbonyolította és elsősorban nem a kétoldali megközelítésre támaszkodott. Fakultatív anyagnak szánta a helyettesítéses és a parciális integrálást.
A középiskolák analízis anyagát 1945 után ideiglenes jelleggel Surányi János és Králik Dezső (1950) dolgozta át. Az 1950-52-es tanterv óriási változásokat hozott. Új szemléletmód, új tananyagrészek kerültek be a középiskolai tananyagba, kimaradt a határérték, a differenciál- és integrálszámítás, helyére jöttek pl. a halmazok, geometriai transzformáció, kombinatorika, valószínűségszámítás, matematika logika, ábrázoló geometria. Péter Rózsa, Gallai Tibor, Hódi Endre, Tolnai Jenő, Varga Tamás, Faragó László neve fémjelzi ezt a korszakot. Az analízis oktatása az egyetemek feladata lett.
Számos irányzat, elképzelés, illetve hozzá tankönyv, példatár készült a folytatásban. Hozzám a Czapáry-könyvek álltak a legközelebb. Nem ragadott meg Peller József és Megyesi László elképzelése, sem Kósa András és Korányi Erzsébet felfogása, sőt az integrál újonnan bevezetett jelölése sem: (pl. 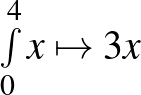 ) a Matematikai feladatok gyűjteménye II. kötetében. Az Összefoglaló Feladatgyűjtemény matematikából XX–XXI. fejezetének feladatai már nem kerültek be az érettségibe.
) a Matematikai feladatok gyűjteménye II. kötetében. Az Összefoglaló Feladatgyűjtemény matematikából XX–XXI. fejezetének feladatai már nem kerültek be az érettségibe.
Következtetések
Hogyan tovább? A kor követelményeinek megfelelően, a modern IKT-eszközök felhasználásával, az analízis alkalmazási szintjének megfelelően, támaszkodva a hagyományokra, konvenciók kialakítása, egy egészséges kompromisszum létrehozása az elmélet, a gyakorlat és az alkalmazás között, biztosítva függvények széles körű ismeretét. Nem kell a középiskolában mindent precízen a megtanítani, szemléletesen elő kell készíteni és felfedeztetni a fogalmakat, de úgy, hogy arra ne mondja majd az egyetemi oktató, hogy „felejtsd el fiam, amit eddig tanultál”. Ne mondjunk ki olyan állítást, amit később korrigálni kellene. Nagyon fontos a tanárok felkészítése az analízis tanítására, másképpen nem megy.
Kövessük az akadémikus Beke Manó tanácsát: „Jól kell megválasztani az időt, amikor az absztrakt fogalom bevezetendő. Ezt a bevezetést mindig előzze meg a kellő előkészítés. Adjuk meg előbb annak az absztrakt fogalomnak tapasztalati, szemléleti, általában érzékelhető elemeit, kapcsoljuk erősen össze a tanulóban meglévő, hasonló rokon, vagy analóg ismeretanyaggal és úgy térjünk rá az absztrakcióra, a fogalmak megalkotására és azoknak a tanuló általános műveltsége szempontjából is értékes anyagon való begyakorlására.”
Irodalom
- [1] Alexits, Gy. (1943): Tanítsunk-e a középiskolában analízist? Mennyiségtani és Term.tud Didaktikai Lapok, Bp. I. 5.
- [2] Barra, Gy. (1944): Tanítsunk-e a középiskolában infinitézimális számítást? Mennyiségtani és Term.tud. Didaktikai Lapok, Bp. II. 1.
- [3] Barra, Gy. (1943): A Mennyiségtan tanítása, Debreceni Könyvek.
- [4] Beke, M. (1967): Bevezetés a differenciál- és integrálszámításba, Gondolat, Bp.
- [5] Beke, M. & Mikola, S. (1909): A középiskolai matematika tanítás reformja, Franklin, Bp.
- [6] Jónás, M. (1945): Mennyiségtan a Gimnáziumok és Leánygimnáziumok VI-VIII. osztálya számára, ORT, Debrecen.
- [7] Rátz, L. & Mikola, S. (1910): Az infinitézimális számítások elemei a középiskolában, Franklin, Bp.
- [8] Tóth, F. (1943): Mégiscsak tanítsunk infinitézimális számítást a középiskolában, Mennyiségtani és Természetttudományi Didaktikai Lapok, Bp. I. 7.
- [9] Veress, P. (1928–1942): Elemi Mennyiségtan a Gimnáziumok és Reálgimnáziumok VI-VIII. osztálya számára, Egyetemi Nyomda, Bp.
Debreceni Egyetem Matematikai Intézet









