Az általános relativitáselmélet alapjait Einstein 1915-re fektette le tíz évnyi nagyrészt magányos kutatás eredményeképpen. Az akkori próbálkozások fősodrából való kilépés a végeredményre is rányomta a bélyegét: más versengő, az elektrodinamikából kiinduló vektor- (elsősorban Lorentz, Poincaré), illetve a klasszikus gravitációelmélet potenciálos megfogalmazását követő skalárelméletekkel (elsősorban Abraham, Mie, Nordström) ellentétben az általános relativitáselméletben a dinamikai változó egy tenzormező és magukat a gravitációs jelenségeket e tenzormező által meghatározott téridő-geometria görbülete írja le. Az elmélet meghökkentő szerkezete ellenére gyors kezdeti sikereket ért el: a Schwarzschild-megoldás 1916-os felfedezésével a Merkúr perihélium-elfordulásának magyarázata, illetve az 1919-es Napfogyatkozás során az elmélet által megjósolt fényelhajlás igazolása Einstein forradalmi elgondolásainak szó szerint is fényes igazolásait adták. Az 1920-as évek során az Einstein-egyenlet kozmológiai megoldását is megtalálták, és ez a belátható Univerzum tágulását jelezte előre: Einsteint ez aggodalommal töltötte el elmélete helyességét illetően, viszont a tágulást Hubble csillagászati megfigyelései 1929-től tényleg elkezdték alátámasztani.
Ezt követően a kibontakozás lelassult. A közismert történelmi eseményeken túl nagyrészt azért, mert az elmélet magvát adó Einstein-egyenlet egy rendkívül bonyolult globális másodrendű nemlineáris parciális differenciálegyenlet, amelynek kezeléséhez a matematikai technikák igazából máig is hiányoznak; emiatt a fizikailag is releváns megoldások halmaza nehezen bővült (habár magának az egyenletnek egyre több ad hoc egzakt megoldása vált ismertté). Az 1960–70-es évek hoztak újabb lendületet, ami a Kerr-megoldás 1965-ös megtalálásán túl az elmélet még részben hiányzó koncepcionális fizikai illetve matematikai alapjainak szisztematikus kidolgozását is eredményezte (Geroch, Hawking, Leray, Lichnerowicz, Penrose és sokan mások). Ennek az elméleti tisztázódásnak a során az is nyilvánvalóvá vált, hogy az einsteini elmélet fizikai szerkezete a fizikatörténetben ismert korábbi elméletekkel ellentétben mélyebben összefonódott a megfogalmazásához felhasznált modern absztrakt differenciálgeometria matematikai szerkezetével (egy gyors példa: mi egy differenciálható sokaság automorfizmusainak vagyis diffeomorfizmusainak fizikai jelentése?). Mindenesetre csupán ekkortól kezdve, vagyis csak mintegy fél évszázada, jóval Einstein halála utántól beszélhetünk az általános relativitáselméletről úgy, mint egy fizikailag és matematikailag is jól megalapozott, a fizikus és matematikus társadalom széles köreiben is elfogadott teóriáról.
De továbbra is, nem állt rendelkezésre elegendő kísérleti megfigyelési adat az elmélet robusztus fizikai jóslatainak ellenőrzésére. Ezek a kísérleti alátámasztások egészen az elmúlt évtizedig várattak magukra: végül is aztán a gravitációs hullámok 2016-os észlelésével, majd az első közvetlen feketelyuk-portré 2019-es elkészültével azt lehet mondani,1 hogy száztíz évnyi kemény, összehangolt elméleti és kísérleti fizikusi valamint matematikusi erőfeszítés eredményeképpen az általános relativitáselmélet bevonulhatott a fizika elméletek pantheonjába.
Azért kezdtük Hraskó Péter Relativitáselmélet című egyetemi tankönyvének (Typotex, Budapest, 2016) recenzióját e rövid történeti beveztővel, hogy nyilvánvalóvá váljék: a gravitációelmélet történetében a nem is olyan rég volt 2010-es évek meghatározó jelentőségűek; ez a történeti észrevétel komoly vonzerővel hathat és már önmagában is indokolja egy ebbe a forrongó, ám igencsak nehéz témakörbe bevezető tankönyv ez idő tájra eső megjelentetését. A könyvet fellapozva azonnal kiderül, hogy a szerző több évtizednyi előadási tapasztalatához és remek előadói képességeihez illően a könyv világos szerkezetű, mondatai szabatosak, s így a könyv nagyon jól olvasható. A könyv kilenc fejezetből áll: először a speciális relativitást tárgyalja (1. Speciális relativitáselmélet (téridő-geometria), 2. Speciális relativitáselmélet (dinamika)); ezt követi a gravitáció einsteini felfogását segítő intiuitív bevezetés (3. A gravitáció mint geometria); az elkerülhetetlenül szükséges szigorúan minimális matematikai eszköztár fölvonultatása (4. A Riemann-geometria alapjai); az elmélet elsődleges szerkezetének áttekintése (5. A pszeudoriemann-téridő és az ekvivalencia-elv); majd az elmélet magva (6. Az Einstein-egyenlet); végül következnek a legfontosabb alkalmazások (7. A magányos csillag térideje, 8. A gravitációs sugárzás, 9. A kozmológia alapjai). A megértést tovább segítik az egyes fejezetekben található feladatok (gyakran részletes megoldásaikkal együtt). E sorok írója különösen megvilágítónak találta a 3. fejezetet, amelyben a szerző eredményesen küzdött meg a motiváció és intiuitív alapozás igen nehéz feladatával. Fontos továbbá a 6.3 alfejezet, amely az általános relativitáselmélet egyik legbonyolultabb problematikájába: a gravitációs energia kérdéskörébe enged bepillantást. (A gravitációs energia kvázilokális természetének fizikai, leírásának matematikai tisztázása máig is aktívan nyitott elméleti kutatási terület, egyelőre igazán megnyugtató válaszok nélkül.) A gravitációs hullámokat és a kozmológiát tárgyaló 8–9. fejezetek fontosságát pedig az adja, hogy a 2010-es évekkel elkezdődött a „gravitációs csillagászat” tudománytörténeti jelentőségű új korszaka.
Zárásképpen következzék egy kritikai észrevétel, amely nélkül egyetlen recenzió sem lehet igazán meggyőző. A könyv mottója így szól: „Jegyezze meg fiatal barátom, hogy a fizikában nem a matematika nehéz, hanem a fizika.” A mondás I. M. Frank szovjet fizikustól származik, aki 1958-ban kapott fizikai Nobel-díjat a Cserenkov-sugárzás elméleti magyarázatáért. A fizikai Nobel-díj említése kapcsán a gravitációelmélet szempontjából nem feledkezhetünk el arról, hogy a brit R. Penrose szintén elnyerte a fizikai Nobel-díjat 2020-ban az általános relativitáselmélet fekete lyukakkal kapcsolatos bizonyos jóslatainak matematikai megfogalmazásaiért (e jóslatokat részben kísérletileg is ellenőrizték a 2019-es feketelyuk-megfigyelésben). (Természetesen ezt a 2016-ban megjelent könyv még nem tartalmazhatta. A szerk. megj.) Penrose matematikus körökben is jól ismert (pl. a Penrose-csempézések kapcsán) olyannyira, hogy jelen pillanatban nehéz lenne megmondani, matematikai vagy fizikai munkássága lesz jelentősebb az utókor számára. Fentebb csupán megemlítettük, hogy az elmélet 1960–70-es évekbeli szisztematikus megalapozása során az derült ki, hogy az elmélet mélyszerkezete inherensen összekapcsolódik bizonyos nehéz differenciálgeometriai problemákkal is. Ezt úgy is átfogalmazhatnánk, hogy immár bő fél évszázada kifinomult differenciálgeometriai ismeretek nélkül az általános relativitáselmélet jelenleg átlátott mélységében már nem igazán művelhető. E fejlődéstörténet visszatükröződését fedezhetjük fel a témával kapcsolatos bevezető könyvek stílusának megváltozásában is, amelyben az ugrást a Hawking–Ellis könyv 1973-as megjelenése jelentette. A Frank-idézet arra vonatkozó törekvéseket fogalmaz meg tömör alakban, hogy „de az általános relativitást tanítsuk továbbra is fizikus módon”. Ezt a szerző a Bevezetésben (l. 10. oldal) azzal indokolja, hogy például a modern absztrakt differenciálgeometria eszköztára lehetővé teszi nem triviális topológiájú sokaságok vizsgálatát is, amelyekre viszont (első ismerkedésben) nincs szükség. Viszont ugyanakkor már az Einstein-egyenlet legelső, legegyszerűbb megoldásai is nem triviális topológiájú sokaságokon adódnak (például a könyvben is tárgyalt nem-kiterjesztett Schwarzschild-, illetve Kerr-megoldások alaptere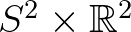 
, és e terekben a fekete lyuk megléte éppen ezzel a ténnyel kapcsolatos abban a formában, hogy a fekete lyuk pillanatnyi eseményhorizontja reprezentálja a 
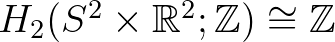homológiacsoport egy generátorát stb.). Sőt az 1980-as évekkel kezdődően matematikusok derítettek fényt arra, hogy már a lehető legegyszerűbb szerkezetű négydimenziós tér, az 
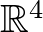is kontinuum sok különböző differenciálható struktúrával látható el (úgynevezett egzotikus vagy hamis 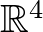-ek)2 és e terek között lokálisan semmilyen módon nem tehető különbség; viszont az Einstein-egyenlet globális megoldásai érzékenyek e struktúra megváltoztatására. Például a mai kutatások egyik központi kérdése: a (szintén Penrose által felvetett) úgynevezett Erős Kozmikus Cenzor Hipotézis érvényessége vagy érvénytelensége szempontjából. Kissé hatásvadászan fogalmazva azt mondhatnánk, hogy az 1980-as évek óta egyre bővülő matematikai ismereteink fényében már a legegyszerűbb szituációról – az általunk tapasztalt lapos téridőről – sem tudjuk megmondani, hogy az a Minkowski-féle téridő-e vagy pedig az Einstein-egyenlet egy még ismeretlen megoldása ismeretlen további tulajdonságokkal. Hogy ez a nyugtalanító lehetőség fizikailag is releváns-e, egyebek közt további differenciáltopológiai vizsgálatokat igényel.
Úgy érezzük, hogy a fizikai és a matematikai gondolkodás éles, de csakis történetileg, tehát tudományfilozófiailag szólva csakis módszertani konvencionalizmussal indokolható különválasztása egy sajátosan magyar jelenség: a hazai fizikus és matematikus közösség évtizedek óta fennálló hermetikus elkülönültségének következménye, mely fizikus oldalról talán Jánossy Lajos, Marx György, matematikus oldalról pedig Erdős Pál öröksége.
Összefoglalva: mindig nagy öröm olyan relativitáselméleti bevezető könyvet kézbe venni, amely a szerző érett oktatási tapasztalatain alapulva didaktikai nehézségeket kerül el, és ezáltal olvasása szinte bizonyosan fiatal fizikusokat fog elindítani ebbe az irányba. Ugyanakkor annak ellenére, hogy az általános relativitáselmélet oktatása sok helyen (így idehaza is) nem szerepel az egyetemi törzsanyagban, annak már a legegyszerűbb bemutatásban is megjelenő koncepcionális és technikai kifejtése időigényessége miatt, az a meggyőződésünk, hogy igazából már az első találkozás során sem érdemes elkerülni az elmélet mögötti (el kell ismerni: nehéz) differenciálgeometriai és topológiai, parciális differenciálegyenletekkel kapcsolatos „sötét hátteret” mert előbb-utóbb úgyis szükség lesz rá. Ahogy W. Pauli (szintén Nobel-díjas fizikus) fogalmaz egyik angol nyelvű levelében: No Time to be Brief.
BME Algebra és Geometria Tanszék
Lábjegyzetek
- 1Előbb itt azért meg kell még említeni a gravitációs vöröseltolódás laboratóriumi megfigyelését; egymás körül keringő pulzárok keringési idejének einsteini elmélet szerinti módosulásának évtizedeken át tartó igazolását; illetve mesterséges holdakon éveken keresztül folyamatos szabadesésben lévő különféle anyagú testek megfigyelésével az ekvivalencia-elv ultrapontos igazolásait is.
- 2Ebben a kontextusban elgondolkodtató, hogy ez a matematikai jelenség az
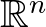-ek között csak akkor lép fel, ha 
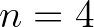, és ez éppen a makroszkopikus fizikai téridő dimenziója.