Válogatás Erdős Pál kedvenc feladataiból

Róka Sándor: Válogatás Erdős Pál kedvenc feladataiból (Typotex, Budapest, 2023)

Erdős Pál (1913–1996) a 20. század egyik legnagyobb hatású matematikusa volt; a matematika számos területén új kutatási irányok kezdeményezője, új módszerek kidolgozója. Jelentőségét érzékelteti az általa írt 1500 cikk, amit összesen közel ötszáz társszerzővel készített el. A magyarországi matematikának is központi alakja, már a sokadik generáció járja az általa megkezdett utakat. Életéről több könyvet is írtak, kettő magyarul is olvasható: Bruce Schecter: Agyam nyitva áll!: Erdős Pál matematikai utazásai. Ford. Gyárfás Vera. Budapest: Park; Vince Kiadó, 1999 és Paul Hoffmann: A Prímember. Scolar Kiadó, 1999. Számelméleti gondolatainak egy részébe bepillanatást ad az először 1959-ben megjelent, Surányi Jánossal írt Válogatott fejezetek a számelméletből című könyv. Örömteli esemény, hogy most megjelent Róka Sándor tollából (klaviatúrájából) egy Válogatás Erdős Pál kedvenc feladataiból.

Erdős Pál matematikáját méltatlan lenne pár sorban jellemezni; jelentőségét, sokrétűségét több konferencia és tanulmánykötet tárgyalta. A matematikusoknak többfajta osztályozása ismert. Az egyik ilyen szerint vannak elméleteket alkotók és vannak problémamegoldók. Erdőst a problémafelvetők és problémamegoldók egyik legnagyobbikának tartja a matematikus társadalom. Sok ezer kérdést vetett fel, csak a számelméleti problémákat egy 128 oldalas, Ronald Grahammel írt Old and new problems and results in combinatorial number theory című könyvben foglalta össze. A cikkeinek többsége a Rényi Intézet honlapjáról elérhető és Grahammel írt könyve is letölthető az internetről.

Erdős a Középiskolai Matematikai és Fizikai Lapok (KöMaL) feladatainak megoldása során köteleződött el a matematika mellett, és ennek hatására egész életében sok olyan feladatot tűzött ki, amelyek mindössze középiskolai tudást, de nagyfokú leleményességet igényeltek. Ezek többsége a KöMaL-ban és a The American Mathematical Monthly-ban jelent meg. Ezekből nyújt válogatást Róka Sándor könyve 65 feladatot közreadva.

A könyv először nyolc oldalon bemutatja Erdős életét saját és kollégái visszaemlékezéseit felhasználva. Utána következnek a feladatok, mindegyik egy-egy új lapon. Külön értéke a könyvnek, hogy a hátterükről is sok mindent elárul, ezek mutatják a feladatok fontosságát, kapcsolatait más kérdésekkel. Persze könnyű lenne kétszer, de akár tízszer ennyit is írni róluk, de ez is épp elég, és ráadásul olvasmányos. A könyv további részeiben megoldások olvashatók, és végül néhány Erdősról szóló írás ajánlásával, köszönetnyilványítással zárul a könyv.

A könyvben szereplő feladatokat a könnyű érthetőség és elegancia jellemzi. Alapvető jellemzője a kombinatorikus kérdésfelvetés, bizonyos dolgok megszámlálása. A feladatok első kétharmada a számelmélethez kapcsolódik, majd utána kombinatorikus halmazelméleti, gráfelméleti és végül geometriai feladatok következnek.

A számelméleti feladatok során bepillantást nyerhetünk Erdős prímszámokkal kapcsolatos elemi bizonyításaiba (Csebisev-tétel, a prímszámok reciprokainak összege divergens); találkozunk oszthatósági feladotokkal (pl. az Erdős–Ginzburg–Ziv-tétel speciális esetei) és sok olyan kérdés is olvasható, amelynek során az első 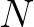pozitív egész közül kell a kiválasztani a lehető legtöbb olyat, amelyik rendelkezik egy adott tulajdonsággal. Itt nagyon eltérő nehézségű feladatokat találhatunk, de ezekről a bevezető informál.

A kombinatorikus halmazelmélet feladatai között az Erdős-Ko-Rado tételt is megtaláljuk, a gráfelméletből a Ramsey-számokra vonatkozó becslések szerepelnek. Így rövid bepillantást kapunk az Erdős által kifejlesztett véletlen módszerbe is. A kombinatorikus geometriát többek között a „Happy end”-problémaként elhíresült, sokcsúcsú konvex sokszöget kereső feladat valamint a gráfelmélet és a geometria kapcsolatát mutató 55. feladat képviseli. Az utolsó feladat a háromszögek geometriájának egyik fontos egyenlőtlensége, az Erdős-Mordell tétel.

Mi az, ami kiemeli Erdős Pál feladatait a versenyekre felkészítő feladatgyűjtemények közül? Az egyik a feladatok egyedisége, ami a megjelenésük idején sokszor szokatlan volt, de most is jól felismerhetővé teszi őket. A másik a szépségük és eleganciájuk. Megragadja az olvasót az, amikor középiskolás szintű fogalmakat használva váratlan összefüggésekre mutatnak rá. Nem begyakoroltatni akar módszereket, hanem minden feladathoz új ötletre van szükség.

Kinek ajánljuk a könyvet? Haszonnal forgathatják a matematikai versenyekre készülő diákok és mindazok, akik örömüket lelik érdekes feladatokon való gondokodáson. A jelen ismertetés írója a kombinatorikus számelmélet kutatója és ő is talált általa nem ismert számelméleti Erdős-feladatot, ezért nyugodtan javasoljuk kutató matematikusoknak is, biztos találnak benne újdonságot.

Végezetül köszönetet mondok Róka Sándornak a könyv megírásáért és mindazoknak, akik segítették a munkáját. Biztosak lehetünk benne, hogy a könyv jelentősen hozzájárul ahhoz, hogy Erdős Pál gondolatai a következő generációk számára is hozzáférhetőek, inspirálóak legyenek.