Lakatos Imre: A gyakorló matematikus filozófiája (Typotex, 2021) https://www.typotex.hu/book/11781/lakatos_imre_mate_a_gyakorlo_matematikus_filozofiaja
A kötet címéről
A kötet a híres tudományfilozófus, Lakatos Imre (1922–1974) dolgozataiból egy összeállítás – szerkesztette Máté András (jelen írás utolsó részében találja az olvasó a kötet tartalomjegyzékét). A dolgozatokat összefogó téma a matematika filozófiája. A kötet címe két szempontból is kissé problematikus. Egyrészt fantáziacím, nem Lakatostól ered. Címnek talán szerencsésebb lett volna csak „A gyakorló matematikus filozófiája” és alcímnek a „Lakatos Imre írásai”. Másrészt, a cím magyarázatra szorul. Alaposabb megértéséhez a kötetnek legalább az első két cikkét lenne érdemes tanulmányozni. Kísérletet teszünk arra, hogy érzékeltessük röviden a cím jelentését.
A 19. sz. végétől a 20. sz. közepéig jelentős fordulatok következtek be a matematika filozófiájában. A fő áramlatok, csak címszavakban, a következők voltak:
1. 19. sz. vége, 20. sz. eleje. Törekvés a matematika cáfolhatatlan és kimerítő megalapozására, azaz az úgynevezett infallibilista megközelítés (többek között, Frege, Russell, Hilbert munkássága). A klasszikus axiomatikus módszer modernizálása, a formalizálás bevezetése, a matematika formállogikai (deduktív) felépítése. Igyekezet átfogó alapok létrehozására (Cantor halmazelmélete). Ezt a korszakot az antinómiák felbukkanása (Russell) zárta le.
2. Törekvések az antinómiák kiküszöbölésére (például Zermelo és Fraenkel halmazelmélete, 1908, 1930). Gödel nevezetes negatív eredménye, a nemteljességi tétel (1931), „valamire való” elmélet konzisztenciája a rendszeren belül megfogalmazható, de nem bizonyítható, következésképpen, mindig létezik az elméletben nem bizonyítható állítás. Gödel eredménye lezárja a fenti 1. korszakot.
3. Gödel tételének hatása. A matematikában sem létezik a világ teljes megismerése, csak fokozatos és relatív megismerés létezik. A nagy rendszerek esetén csak relatív ellentmondástalansági bizonyítások léteznek. Az axiómákat és konzisztenciájukat végső soron nem a logikai eszközök, hanem, hosszú távon, a tapasztalás igazolhatja. Nincs éles különbség a matematika és a természettudományok módszere között (legfeljebb az alkalmazott dedukció mennyiségében van különbség). Ez a matematikának egy fallibilista megközelítése, úgynevezett empirista megközelítés.
Lakatos alapjában véve egyetért az empirikus megközelítéssel, de azt kissé módosítja és más megvilágításba helyezi, máshová teszi a hangsúlyokat. Nála nincs súly a deduktív felépítésen és az axiómákon, hanem szerinte a matematika középpontjában a problémák (a hipotézisek, sejtések) állnak. Szerinte ezeket elsődleges vizsgálni. Vagy logikai visszavezetéssel, tehát redukcióval egyszerűbb problémákra (végső soron axiómákra), vagy/és tapasztalással. Szükséges a problémát alaposan elemezni, több oldalról megvilágítani. Nagy jelentőséget tulajdonít a cáfolat módszerének. Lakatos nagyjából ezeket érti a gyakorló matematikus filozófiáján. Megközelítését kvázi-empirizmusnak nevezi.
Érdemes mindehhez hozzátenni, hogy nagy hatással volt Lakatosra Pólya György munkássága (többek között A problémamegoldás iskolája c. műve). Ennek is része volt abban, ahogyan összekapcsolódik Lakatos absztrakt filozófiája és a gyakorló matematikus fogalma. Ezután önvizsgálatot tarthatnak a matematikusok, hogy hozzájuk az empirista, a kvázi-empirista matematikafilozófia, vagy esetleg egy harmadik megközelítés áll-e közelebb.
Tévedett-e Cauchy?
(nemstandard valós számok, nemstandard analízis)
A kötetben egyetlen olyan matematikai problémát találunk, amelyet Lakatos részletesen elemez, a folytonos függvények egyenletesen konvergens sorozatai határfüggvényének folytonosságára vonatkozó híres Seidel-tétel állítását (3. dolgozat). Ismertetjük tömören Lakatos írását.
Ismert a matematikatörténetből, hogy a matematika precízzé tételének nagy úttörője, Cauchy, a következő, az utókor által „hibásnak” tartott tételt bizonyította: Folytonos függvények bármely sorozatának limeszfüggvénye is folytonos.
Hiányzott a konvergáló függvények sorozatára az egyenletes konvergencia feltétele. Könnyű példát találni arra, hogy az egyenletes konvergencia feltétele nélkül Cauchy tétele hamis. Ilyen példa már Cauchy korában ismert volt, sőt maga Cauchy is ismerte. Nem nehéz Cauchy bizonyításában megtalálni a „hibát”.
Maga Cauchy kissé ingadozott. Egyrészt hitt tétele igazában. Másrészt, ismerve az ellenpéldát és a kritikákat, érezte, hogy létezik valami tisztázatlanság a tétele körül. A problémához hasonlóan viszonyult híres pályatársa, Abel is. Több évtizedig tartott, amíg Seidel megalkotta az egyenletes konvergencia fogalmát, és bizonyította a tétel egyenletes konvergenciával kiegészített változatát. Igazi „rejtélynek” tűnik, hogy olyan zseniális matematikusok, mint Cauchy vagy Abel, miért bizonyultak szűklátókörűnek ebben a kérdésben?
A rejtély csak akkor került közelebb a megoldáshoz, amikor 1960 körül Abraham Robinson megalkotta a nemstandard valós szám fogalmát, és létrehozta az arra épülő elméletet, a nemstandard analízist. Ez az elmélet a matematikailag addig kétesnek tekintett Leibniz-féle infinitezimális elmélet precíz megvalósításának és kiterjesztésének tekinthető. Robinson azt állította, hogy elméletében interpretálva, helyes Cauchy tétele. Azaz, ha valós számon nemstandard (akár végtelen) valós számot értünk, konvergencián nemstandard konvergenciát, akkor Cauchy eredeti tétele igaz. Visszapergetve a tudománytörténetet, tudjuk, hogy Cauchy, vagy Abel még a Leibniz-féle infinitezimális elmélet hatása alatt állt. Vagyis Robinson szerint a kritikus tétel mögött egy mai nemstandardnak számító (nemstandard valósakra épülő) tétel áll. Seidel viszont a közönséges valós számokra bizonyította tételét, tehát annak ma is ismert, hagyományos alakját bizonyította. Seidel tehát nem értette meg Cauchyt és viszont, két malomban őröltek. Csavar a történetben, hogy azóta tudománytörténészek kiderítették, hogy Cauchy még csak nem is pontosan a robinsoni értelemben értette tételét, hanem egy ahhoz közel álló verzió szerint.
A történet számos tanulsággal szolgál a tudománytörténet számára. Például azzal, hogy milyen fontos mélyre ásni az állításoknál a felhasznált alapfogalmakat illetően. De nemcsak a fenti történet tanulságos, hanem a benne foglalt nemstandard valós számnak (és a nemstandard analízisnek) létrejötte is – jelen sorok írója szerint. Ez önmagáért is megér egy kis kitérőt.
Leibniz a maga korában megalkotta és sikeresen használta az infinitezimálisok elméletét, de az elmélet nem tudott kiteljesedni. Hosszú próbálkozások után sem sikerült az elméletet precízzé tenni matematikailag. A gordiuszi csomót később Weierstrass vágta el, amikor létrehozta a határérték fogalmának egy egészen más definícióját, az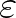 
-
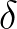-s definíciót. Ez elterjedt és sikeres lett. A Leibniz-féle elméletet tulajdonképpen már el is temették, amikor Robinson váratlanul rátalált azokra a modern keretekre, amelyekben a Leibniz-féle elmélet egy változata precízen rekonstruálható, sőt elmélyíthető.
A „régi-új” elméletet azonban mégsem fogadta az a lelkesedés a matematikusok körében, ami talán elvárható lett volna Leibniz elméletének kb. 300 éves tetszhalála után. A következő kérdések merülnek fel:
1. Robinson eredményeit elemezve kiderült, hogy ahogyan egy szokásos valós szám racionális számok konvergens sorozataival azonosítható, úgy egy nemstandard valós szám hagyományos valós számok konvergens (vagy végtelenhez tartó) sorozataival azonosítható. Vagyis a nemstandard valós szám a hagyományos valós szám egy kézenfekvő általánosítása. Miért nem fedezték fel ezt a fogalmat 300 évig?
2. A konvergencia leibnizi megközelítése (az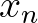 
valós sorozat konvergál 
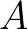-hoz, ahol 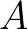véges, ha az 
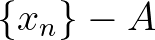nemstandard szám egy infinitezimális) természetesebbnek tűnik, mint Weierstrass 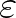--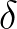s definíciója. Miért tartunk még mindig ki kizárólagosan, például az oktatásban, a Weierstrass-féle definíció mellett? Hasonló mondható például a függvény folytonosságának definíciójáról is.
3. Számos klasszikus valósanalízisbeli tétel elegánsabban, természetesebben bizonyítható (az általánosításnak számító) nemstandard analízisben, mint a hagyományosban. Hasonló jelenséggel találkozhatunk például a komplex függvénytanban. De, amíg a komplex függvénytanban örülni tudunk ezeknek a szép bizonyításoknak, és tanítjuk őket, addig ritkán hallunk a fent idézett nemstandard bizonyításokról.
Az 1. kérdéssel kapcsolatban az juthat eszünkbe, hogy a matematika fejlődése nem egyenes vonalú. Például a negatív szám fogalma egyidejűleg jött létre a komplex szám fogalmával. A 2. és 3. kérdés megválaszolása talán meghaladja a matematika filozófiájának kereteit, és csupán az új felfedezések elfogadásának tehetetlenségére, lassúságára vezethető vissza.
Kiket szólít meg a kötet?
A kötet tartalomjegyzéke a következő:
Előszó (Máté András): Lakatos Imre – egy nyugtalanító gondolkodó
1. A végtelen regresszus és a matematika alapjai
2. Az empirizmus reneszánsza a mai matematikafilozófiában?
3. Cauchy és a kontinuum: A nemstandard analízis jelentősége a matematika történetéban és filozófiájában.
4. Mit bizonyít egy matematikai bizonyítás?
5. Az analízis és szintézis módszere
6. A szükségszerűség. Kneale és Popper.
7. Változások az induktív logika problematikájában.
8. A tudomány társadalmi felelőssége.
Irodalom
Az Előszó szerint a dolgozatok matematikusokhoz és filozófusokhoz is szólnak. Úgy foglalnék állást, hogy az 5., 6. és 7. dolgozat jobbára filozófusok számára emészthető, míg a 3., nemstandard analízisről szóló dolgozat inkább a matematikusok számára. Kiemelném az empirizmussal foglalkozó 2. dolgozatot, amelyik leginkább kapcsolódik a kötet címéhez. Külön csemege, hogy a kötet több dolgozatát Lakatos nem a nyilvánosságnak szánta, e dolgozatok első ízben jelennek meg magyarul (lásd a kötet lábjegyzeteit).
A kötet dolgozatai ugyan 1974 előtt készültek, de a szerkesztő kiemeli, hogy a mondanivaló napjainkban a reneszanszát éli. Azonban úgy gondolom, hogy a hetvenes évek óta történtek a matematikában átütő változások – ilyen például az algoritmikus, a számítógépes szemlélet, vagy a rendszerszemlélet térhódítása – ezek a változások, értelemszerűen, a matematika filozófiáját is befolyásolják (például sokat foglalkozott a matematika azzal, hogy mely egyenletekhez található „megoldóképlet”, de ma már megoldottnak tekinthetjük az egyenletet azzal is, ha a gyökök meghatározására ismerünk algoritmusokat).
Mindent egybevetve, a kötet cikkei kiváló gondolatébresztők, mint Lakatosnál általában. A matematika filozófiája iránt érdeklődőket nem kényeztetik túlságosan el napjainkban értékes olvasmányokkal, ezért is üdvözöljük a nagy gonddal készített összeállítást.