Lakatos Imre: A gyakorló matematikus filozófiája (Typotex, 2021) https://www.typotex.hu/book/11781/lakatos_imre_mate_a_gyakorlo_matematikus_filozofiaja
Lakatos Imre, aki a tudományfilozófia és a matematikafilozófia nemzetközi porondjának egyik központi alakjává vált, tanulmányait a Debreceni Tudományegyetemen kezdte matematikából, fizikából és filozófiából, ahol 1946-ban doktorált „A természettudományos fogalomalkotás szociológiája” című dolgozatával. A második világháborút követő viharos években politikai szerepet vállalt, miközben nagyobb számban jelentetett meg főként publicisztikai szintű tanulmányokat a tudomány lehetőségeiről és társadalmi szerepéről a kommunista keretek között. Ám gyorsan ívelő karrierje derékba tört, amikor internáló táborba zárták (1950–53). Ezután az MTA Alkalmazott Matematikai Intézetében kapott állást mintegy „mentőövként”. 1956-ban disszidált Magyarországról.
Második doktori értekezését a Cambdridge-i Egyetemen írta az ötvenes évek végén, matematikatörténeti és matematikafilozófiai témából. 1960-tól Karl Popper, a világhírű tudományfilozófus tanítványa és kollégája, majd később utódja lett a London School of Ecomonics Filozófiai, Logikai és Tudománymódszertani Tanszékén. Ebben az időszakban elsősorban tudományfilozófiai tárgyú cikkeket publikált, és újszerű elképzeléseivel, tudományos felkészültségével, valamint részletgazdag és szabatos érvelési stílusával hamar a nemzetközi élvonalba került. Karrierje csúcsán, 1974-ben hunyt el váratlanul.
Lakatos sosem jelentetett meg egy magnum opust, amely összefoglalná – egyébként talán reménytelenül szerteágazó – nézeteit. Legfontosabb szövegei három posztumusz kötetben láttak napvilágot. A cambridge-i doktori disszertációját, mely továbbdolgozott formában folyóiratcikkekben is megjelent, végül 1976-ban adták ki könyvként Proofs and refutations címmel. A magyar fordítás (Bizonyítások és cáfolatok) viszonylag hamar, 1981-ben kijött. Általánosabb tudományfilozófiai tanulmányai képezték a Philosophical Papers 1. kötetének anyagát, amely 1978-ban jelent meg The Methodology of Scientific Research Programmes címmel. Ezen írások zöme megtalálható a Lakatos Imre tudományfilozófiai írásai című fordításgyűjteményben (1997). A Philosophical Papers 2. kötete főként a matematika- és logikafilozófiai témájú cikkeit közölte szintén 1978-ban, Mathematics, science and epistemology címmel, ám ezek a nagy hatású írások ezidáig nem voltak fordításban elérhetők. Ezt a mulasztást orvosolja A gyakorló matematikus filozófiája című, hiánypótló mű.
Az igényesen kivitelezett kötet szerkesztését Máté András végezte el messzemenő alapossággal és kompetenciával, akinek a bevezető tanulmányát bátran ajánlhatjuk az alábbi rövid ismertetés elmélyítése céljából. A fordítások a legkiválóbb szakemberek, jelesül Benedek András, Forrai Gábor, Kiss Olga és Máté András munkái. A kötetet a Typotex Kiadónak és az MTA támogatásának köszönhetjük.
Lakatos matematikára vonatkozó nézeteit talán azzal érdemes bevezetni, ha megnevezzük azt a három fő forrást, amelyet a második disszertációjának köszönetnyilvánításában megjelölt mint legfontosabb inspirációit (lásd a jelen kötet 99. oldalának szerkesztői jegyzetét): Popper kritikai filozófiáját, Pólya matematikai heurisztikáját és Hegel dialektikáját.
1. Popper kritikai filozófiája. A hatvanas évek elején, amikor a legnagyobb figyelmet szentelte a matematika filozófiájának, Lakatos erőteljesen Karl Popper intellektuális befolyása alá került. Ugyan Popper az empirikus tudományok filozófiájával foglalkozott, ám Lakatos megtalálta annak a módját, hogy a popperi filozófia legfontosabb elemeit lehetőség szerint átemelje a matematikafilozófia területére, ahogy az már a szövegei címadásából is kiderül: erre utal cambridge-i doktori disszertációjának címe is, a Logic of Mathematical Discovery (vö. Popper: Logic of Scientific Discovery, 1959), illetve az ebből később összeállított könyv címe, a Proofs and Refutations (vö. Popper: Conjectures and Refutations, 1962).
Poppernél az empirikus elméletek legfontosabb tulajdonsága a cáfolhatóság, a „falszifikálhatóság”; Lakatos ezzel párhuzamosan hangsúlyt fektet mind a matematika „kváziempirikus” jellegére, vagyis a tapasztalati tudományokkal mutatott hasonlóságaira, mind pedig a matematikai cáfolatok jelentőségére. A tudás megalapozásának hagyományos kérdése a cáfolható, nem tévedhetetlen matematika esetén éppúgy értelmetlenné válik, mint ahogy Popper „fallibilis”, tévedéseknek kitett tudományfelfogásában: a megalapozásra törekedő formalista matematikafilozófia egy kalap alá kerül a hasonló szándékú pozitivista tudományfilozófiával. A Popper és Lakatos számára egyaránt fontosabb kérdés azt firtatja, hogy miként hozhat létre a tudósok többé-kevésbé esetleges (és külső tényezők által befolyásolt) tevékenysége objektív, racionálisan megindokolható tudást. A választ – mindkét szerző – a kritikai vita lehetőségében és „tudástermelő” szerepében találta meg.
2. A Pólya-féle matematikai heurisztika. Lakatos az Alkalmazott Matematikai Intézetben töltött évei során ismerkedett meg Pólya György heurisztikai elméletével, sőt Pólya talán leghíresebb írását, a How to Solve It című könyvet ő fordította magyarra (A gondolkodás iskolája, 1969). Pólya az elméletek formális aspektusai helyett a matematikai tevékenység informális vonatkozásaira hívta fel a figyelmet. Ezért őt sem a matematikafilozófia hagyományos problematikája, az elméletek megalapozásának kérdése izgatta, hanem a matematikai problémák megoldásának heurisztikus eljárásait, vagyis intuitív „ökölszabályait” próbálta megállapítani. A heurisztika vizsgálata lehetővé teszi Lakatos számára, hogy kilépjen az „igazolás kontextusának” szigorú, formális korlátai közül, és a „felfedezés kontextusába” tartozó matematikai gyakorlat egycsapásra az elméletek fejlesztésének közegévé válhat. A formális és informális területek folyamatos kölcsönhatásának és szerves egymásra utaltságának tanulmányozásával sajátos válasz kínálkozik a tudás gyarapodásának kérdésére.
3. A hegeli dialektika. A hegeli filozófia hatása, elsősorban a marxista-lukácsiánus álláspontjának köszönhetően már igen korán, a negyvenes évek közepétől megfigyelhető Lakatos gondolkodásában. Bár később – hirdetett szándékai szerint – élesen szembefordult korábbi filozófiai alapállásával, a hegeli hatás mindvégig meghatározó módon jelen van írásaiban, és helyenként expliciten is alkalmazta a hegeliánus fogalmakat és nézeteket. Lakatos mindig ellenérzésekkel viseltetett az olyan filozófiák iránt, melyek merev, történetietlen és reflektálatlan fogalmi sémában próbálják megragadni tárgyukat, és ez az ellenérzés különösen hangsúlyos a matematikai tárgyú vizsgálataiban. Így a formalista nézetekkel szemben a matematikai fogalmak fejlődésének dialektikáját próbálta kidolgozni, miközben szem előtt tartotta mind a filozófia történeti szituáltságát, mind pedig a történetírás filozófiailag irányított természetét.
Mindezek bővebb kifejtéséhez most vegyük szemügyre azt a korban uralkodó matematikafelfogást, a formalizmus és a logicizmus elemeiből gyúrt bevett nézetet, amellyel Lakatos szembeszállt. Ez a felfogás a matematikát formális elméletekkel azonosítja, vagyis mesterséges és szimbolikus nyelven megfogalmazott, axiomatikus-deduktív rendszerekkel. A logicisták szerint (mint Gottlob Frege és a fiatal Bertrand Russell) szerint a matematikai axiómák bizonyossága a logikai intuícióból származik. Ez azt jelenti, hogy a matematika axiómái tulajdonképpen logikailag igaz állítások (tautológiák), tagadásuk pedig önellentmondás. Ebben az esetben a matematika tételeinek igazsága ugyanabból a forrásból táplálkozik, mint a matematikai bizonyítások helyessége, vagyis a logikából, amely viszont – a hagyományos elképzelés szerint – megkérdőjelezhetetlen. A matematika tehát minden kétségen felül tévedhetetlen tudomány.
Egy a priori logikai intuíció működésének feltételezése azonban védhetetlen álláspontnak bizonyult. Abban a fregei logikai elméletben, amelyik egy ilyesfajta intuícióra épít, ugyanúgy ellentmondások lépnek fel, mint a szintén csak tiszta alapfogalmakból kiindulni kívánó naiv halmazelméletben (lásd pl. Russell-paradoxon). Az ellentmondások kiküszöbölése érdekében Russell önkényes és túl szigorú korlátokat szabott a matematika számára (a típusokra vonatkozó megszorításával), és ráadásul kénytelen volt olyan axiómákat is alkalmazni (pl. kiválasztási axióma, reducibilitási axióma), melyeket semmiféle a priorinak tűnő logikai intuíció nem támaszt alá. Az ellentmondásokat „elegánsabban” kiküszöbölő elmélet, a Zermelo-féle axiomatikus halmazelmélet irányába történő elmozdulás a logicista program elárulását jelenti, hiszen a halmazelméleti axiómák némelyike semmiképpen sem tarthat igényt az intuíció, pláne egy tévedhetetlen intuíció általi igazolásra.
A matematika megalapozására irányuló vállalkozások közül David Hilbert formalista programja bizonyult a legsikeresebbnek. Ha a logicista program kudarcát az ellentmondások okozták, akkor az alapokat biztosítani kívánó elmélet legfőbb feladata abban áll, hogy a matematika olyan felépítését kínálja, amelyik bizonyíthatóan mentes az ellentmondásoktól. Ennek érdekében a hilberti felfogás formális, axiomatikus-deduktív szintaktikai kalkulusokkal azonosítja a matematikai elméleteket, melyekkel szemben két fő követelményt támaszt: a kalkulus legyen egyfelől ellentmondásmentes, másfelől pedig teljes, vagyis – ez utóbbi követelmény szerint – minden olyan tételt, amely az elmélet nyelvén megfogalmazható, képesek legyünk vagy bizonyítani, vagy pedig cáfolni. A matematikai elméletek tehát szigorúan véve tartalmatlan, jelentés nélküli szimbólumrendszerek, és az interpretáció művelete, mellyel jelentést tulajdonítunk nekik, már nem matematikai tevékenység.
Ahhoz tehát, hogy a matematikai tudást valamilyen értelemben biztos alapokra helyezzük, e felfogás szerint nem maguknak a matematikai elméleteknek kell alapot keresni (hiszen azok teljesen szabad és önkényes konstrukciók), hanem a formális-deduktív rendszerek tulajdonságaira vonatkozó elméletnek, az ún. metamatematikának vagy bizonyításelméletnek. Ez az elmélet azonban Hilbert igényei szerint sem nem formális, sem nem axiomatikus, ugyanis egyfajta biztos intuícióból merítkezik, és ennek megfelelően csak szigorúan véges és konstruktív eszközöket enged meg. Ez a hivatkozás az a priori intuícióra mutatja (Lakatos szerint), hogy a formalista program hívei végső soron a matematika eukleidészi felfogását vallják (lásd alább), és ezt támasztja alá az is, hogy a formalisták a matematikát kizárólag bizonyító jellegű tudománynak tekintik.
E program kudarcára – ismét csak Lakatos szerint – 1931-ben derült fény, amikor is Kurt Gödel két híres nemteljességi tétele bebizonyította, hogy a formalista filozófiának mindkét alapkövetelménye tarthatatlan: egyetlen, a matematika céljaira elég erős kalkulus sem lehet szintaktikai értelemben teljes, és egyetlen ilyen kalkulus sem képes bizonyítani magáról a konzisztenciát. Lakatos elismeri, hogy a matematikusok közösségének jelentős hányada még nem adta meg magát ennek a kudarcnak, és a Gödel-tételek negatív eredményeit a metalogikában, a bizonyításelméletben és hasonló területeken próbálják megkerülni. Ám minden ilyen kísérlet kilép a formalista program eredeti keretei közül, hiszen feladja Hilbertnek a bizonyításelméletre vonatkozó azon követelményét, hogy az szigorúan csak „intuitíve alátámasztott” eszközöket használhat.
Ahogy Lakatos kifejti, ezek a kritizált metamatematikai programok egyaránt eukleidészi jellegűek (lásd az 1. ábrát), azaz az igazságot az alapállítások szintjén igyekeznek biztosítani, amely – deduktív elméletek lévén – továbböröklődik az alapállításokból levezetett tételekre. Ha tehát sikerülne biztosítani az axiómák kétségen felüli igazságát, akkor azzal a matematika tévedhetetlen tudománnyá válna. Ahogy láthattuk, Lakatos szerint ez a próbálkozás sikertelennek bizonyult, hiszen sem a logikai intuíció, sem a véges és konstruktív eszközökre alapozott eljárások nem képesek megalapozni a formális rendszerek igazságát. Érdemesebb tehát egy fallibilista, popperi ösztönzésű keretben értelmezni a matematikát, amely „kváziempirikus” rendszerként tekint rá, vagyis az igazságérték a következmények, levezetett tételek szintjén kerül az elméletekbe. Innen ugyan nem tud „felfelé” öröklődni, hiszen a levezetett konklúziók igazsága nem garantálja a kiinduló alaptételek igazságát, ám amennyiben kiderülne, hogy egy tétel hamis, akkor ez a hamisság már maga után vonja az alaptételek (legalább egyikének) hamisságát, vagyis popperi értelemben megcáfolja az elméletet.
| Az eukleidészi rendszer | A kváziempirikus rendszer |
 |
 |
1. ábra: Az érett tudományos elméletek két alaptípusa Lakatos szerint – melyekből valójában csak a jobb oldalit tartja plauzibilisnek.
De hogyan gondolja Lakatos, hogy a matematikai elméletek megcáfolhatók? Miként a „kváziempirikus” elnevezés sugallja, itt nem léteznek olyan szinguláris, térben és időben meghatározott, érzékszervek szolgáltatta tapasztalati tények, amelyek az empirikus elméleteket érvénytelenítik. A matematikára jellemző cáfolatok egyik típusát, a formális cáfolatokat az alaptételekből levezetett logikai ellentmondások jelentik. Mivel a matematika abszolút konzisztenciabizonyítása (a hilberti értelemben) kivitelezhetetlennek bizonyult, ezért egy ilyen logikai cáfolat lehetőségével mindig számolni kell. Az alaposan próbára tett, jól bevált elméletek esetében ez persze nem több, mint egy tisztán logikai eshetőség, hiszen az ellentmondás jelenléte igen valószínűtlen. Születőben lévő elméleteknél azonban szem előtt kell tartani ezt a lehetőséget, ezt bizonyítja például a naiv halmazelmélet bukásának története, vagy az infinitezimálszámítás fogalmi kudarcsorozata a Cauchy–Weierstrass-féle „szigorúság forradalma” előtt.
A cáfolatok másik, az előzőnél jóval fontosabb típusát nyújtják az informális cáfolatok. Ezek akkor lépnek fel, amikor a formális elmélet képtelen kielégítő leírást adni az intuitív elképzelések azon csoportjáról, amelyik a formalizálást megelőző ún. informális elméletet alkotja. A formális elmélet ugyanis semmi több, mint egy tetszőleges szintaktikai „játék”, amely csak akkor használható a matematika céljaira, ha képes kielégítően megragadni a tárgyát, az intuíció és a korábbi matematikai tevékenység által felismert (létrehozott) objektumok birodalmát. Ez a fajta cáfolat persze akár figyelmen kívül is hagyható, hiszen a matematika saját, formális nyelvén nem jut kifejezésre, így aztán ez a jelenségtípus teljesen érdektelen, sőt értelmetlen a metamatematika ideálját követő matematikafilozófiák számára. Ám számos matematikus mégis elégedetlen az informálisan cáfolt elméletekkel – Lakatos példaként hozza fel a sokaságok Riemann-féle elméletét (amely nem tudott számot adni a Möbius-szalagról), a Kolmogorov-elméletet (amely értelmesnek tűnő kérdéseket képtelen megválaszolni), vagy a Zermelo–Frankel-féle halmazelméletet (amelyben a kontinuum-hipotézis kérdése eldönthetetlennek bizonyult).
Világos tehát, hogy Lakatos szerint a matematikai tudás nem pusztán szintaxis, hanem szól valamiről. Pólya hatására Lakatos komoly szerepet tulajdonított a matematikai felfedezés olyan elemeinek – pl. induktív általánosítás, analogikus érvelés, gondolatkísérletek –, melyeket általában a „valódi” matematikai tevékenységen kívülre, annak előszobájába szokás utalni. Ezek az eljárások – és az analízis és szintézis részben hozzájuk kötődő módszerei – segítenek felfedezni és egyre pontosabban megragadni a matematikai elmélet tárgyát. Hiszen a matematikai elméletek sosem formális kalkulusokként adódnak a matematikusok számára, hanem ellenkezőleg, a formális elméleteket a matematikusok hozzák létre, méghozzá azzal a céllal, hogy precíz, logikailag áttekinthető keretbe foglalják a már eleve meglevő informális elméleteiket. A formalizálás szerepe éppen abban áll, hogy az informális, az intuíció bizonytalanságával terhelt elméleteket alávesse az egzakt, logikus fogalmi elemzés lehetőségének. A bizonyítás és a bizonyításelemzés kölcsönhatása a fogalmak, kijelentések és módszerek egyre pontosabb meghatározásához vezet. Ez a formalizálási és pontosítási folyamat teszi lehetővé a matematikai ismeretek fejlődését, a tudás növekedését.
Bár e kötet csak rövidebben utal a Bizonyítások és cáfolatok téziseire (főként a 4. fejezeten keresztül), de érdemes megjegyezni, hogy Lakatos abban a művében fejti ki hosszasan és mesteri módon, egy „ideális” tantermi dialógus formájában az elméletek fejlődésére vonatkozó elképzeléseit. Itt a diákok a tanár segítségével rekonstruálják azt a történetet, amely a Descartes–Euler-féle poliéder-sejtés felbukkanásától az axiomatikus algebrai topológia születéséig ível, és amelyben kezdettől fogva jelentős szerepet játszottak a szemléletes gondolatkísérletek, ellenpéldák és bizonyításkritikák. A részletek mellőzésével a 2. ábra érzékelteti, milyen főbb lépések ciklikus bejárására van szükség ahhoz, hogy létrejöjjön egy formális, euklidészinek tűnő rendszer.
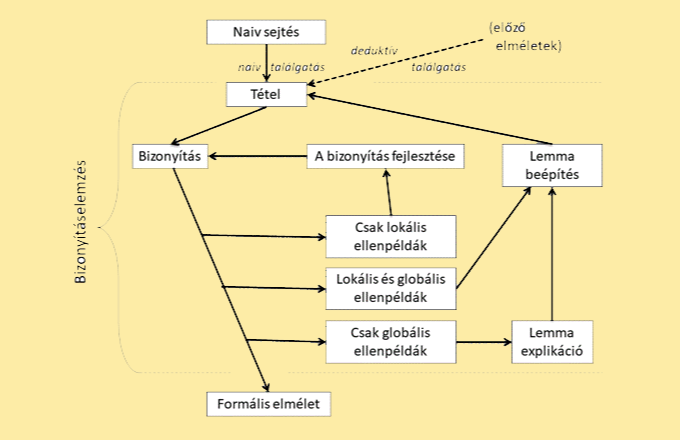
2. ábra: A matematikai elméletek fejlődésének folyamatábrája a Bizonyítások és cáfolatok alapján rekonstruálva
A formális elméletek azonban csupán végtermékei – a kötet címével élve – a „gyakorló filozófus” tevékenységének, és ha ezekre fókuszál a matematikafilozófia, akkor az olyan, mintha az élettant azonosítanánk a holttestek elemzésével (Bizonyítások és cáfolatok, 16. o., jegyzet). A lényeg – vagyis a matematikafilozófia tárgya – az a folyamat, amely során a létrejönnek ezek a tárgyukat már pontosan, de kiüresedve megragadó elméletek, vagyis az a mód, ahogyan a matematikai tudás fejlődik és gyarapszik.
Végezetül röviden utalnánk arra, hogy bár Lakatos sosem írt egy szintetizáló elemzést, ám a matematikáról alkotott elképzelései számos ponton összecsengenek általános tudományfilozófiai nézeteivel. Mindkettőben komoly szerepet kap a heurisztika, amely részint negatív (mit nem szabad csinálni) és részint pozitív (mit akarunk elérni, és milyen elköteleződésekhez ragaszkodunk). Mindkét területen nagy hangsúlyt fektetett mind a cáfolatokra és azok szerepére a „kutatási programok” javításában, mind pedig azokra a módokra, ahogyan a tudósok szembeszállnak a cáfolatokkal. Azok közé a szerzők közé tartozik (kisebb mértékben Popperral, nagyobban Thomas Kuhnnal egyetemben), akik a tudománytörténet szerepére irányították a figyelmet a tudományfilozófiában.
Lakatos is szorosan összetartozónak véli e két területet: „a matematika története, a filozófia iránymutatását nélkülözve, vakká, a matematika filozófiája, mellőzve a matematika történetének legérdekesebb problémáit, üressé válik” (Bizonyítások és cáfolatok, 15), majd rövidítve megismétli ezt az állítást (amely Kant egyik tézisének parafrázisa) az egyik legfontosabb tudományfilozófiai írásának kezdőmondataként: „A tudományfilozófia a tudománytörténet nélkül üres, a tudománytörténet a tudományfilozófia nélkül vak.” (Lakatos Imre tudományfilozófiai írásai, 65.) Amint haszontalan dolog úgy filozofálni a tudományról és a matematikáról, hogy nem vesszük figyelembe annak valódi történetét, hasonlóan lehetetlen olyan történetet írni róluk, amely ne igazodna előzetes elvárásainkhoz és ítéleteinkhez. Ez utóbbit felismerve feladatunk, hogy tudatosítsuk ezen filozófiai elemek jelenlétét és működését, így szándékosan „racionális rekonstrukciót” kínálva a valódi történetről, amely felfedi a történeti és kulturális esetlegességek mögött a matematika belső, valódi logikáját, vagyis azt, amit a „gyakorló matematikus” felfedez és követ a cáfolatok és a kritikai diszkusszió hatására.
Megjegyzések
- 1. Ez az ismertetés főleg egy korábbi, a témát bővebben kifejtő tanulmányon alapul: Kutrovátz Gábor: „3.4.2. Lakatos matematikafilozófiája” In Gulyás László, Kampis György, Kutrovátz Gábor, Ropolyi László, Soós Sándor, Szegedi Péter: Bevezetés a tudományfilozófiába. Budapest: ELTE, 2013, 61–68. (Elérhető online: https://ttk.elte.hu/dstore/document/855/book.pdf.) Ezt a szöveget itt rövidítve és átdolgozva közöljük.
- 2. Molnár Zoltán Gábor recenziója is megjelent (ezúttal nem az Érintőben), A heurisztika gerillaharcosa címmel, itt olvasható: https://www.typotex.hu/review/11781/3883/a_heurisztika_gerillaharcosa