Vetier András négykötetes (kötetenként átlag 133,5 oldalas) Valószínűségszámítás című tankönyve – amelyet a Matematika A4 - Valószínűségszámítás villamosmérnököknek című tárgyhoz írt – nemrég jelent meg elektronikus formában a Typotex kiadó gondozásában:
https://www.typotex.hu/book/11526/vetier_andras_valoszinusegszamitas_1
https://www.typotex.hu/book/11533/vetier_andras_valoszinusegszamitas_2
https://www.typotex.hu/book/11535/vetier_andras_valoszinusegszamitas_3
https://www.typotex.hu/book/11536/vetier_andras_valoszinusegszamitas_4
A szerzőt harmadéves matematikus hallgatóként ismertem meg. Az általa vezetett Sztochasztikus folyamatok gyakorlatok elmélyítették a valószínűségszámítás iránti érdeklődésemet. Most már több mint 10 éve vagyunk munkatársak a BME Sztochasztika Tanszékén. Az évek során végtelenül sokat tanultam tőle. A tanítás iránti elkötelezettségét jól mutatja, hogy ha az órabeosztásban az szerepelt, hogy a Matematika A4 tantárgyához én gyakorlatokat fogok tartani a szeptemberi félévben, akkor sokszor már júliusban írt nekem és a többi gyakorlatvezetőnek, és megosztotta velünk az elképzeléseit. A következő történet is sokat elárul róla. Egy időszakban hangszálproblémák miatt ideiglenesen elment a hangja. Néhány órát úgy oldott meg, hogy a táblára írt, és a hallgatókat kérte meg, hogy szóban interpretálják a leírtakat. A hallgatók nagyon segítőkészen és meglehetősen aktív figyelemmel fogadták a szokatlan helyzetet.
Vetier András első, mérnökhallgatóknak szánt valószínűségszámítás témájú [1] tankönyve 1981-ben jelent meg. A mű 1986-ban elnyerte az Oktatási Miniszteri Nívódíjat. Ezt az 1991-ben megjelent nagyobb terjedelmű [2] könyv követte. A 21. század hajnalán András érdeklődése a valószínűségszámítás oktatásának számítógépes szimulációkkal való kiegészítése felé fordult. 2011-ben megjelent angol nyelvű [3] könyvében Excelben készített szimulációkkal tette befogadhatóbbá a tananyagot.
A fenti felsorolást látva felmerül a kérdés: akkor miért volt szükség egy új jegyzetre? Hasonlóan ahhoz, mint amit Andai Attila recenziójában a 2019. júniusi Érintőben leírt, itt is a szerző újító, kísérletező attitűdje szolgáltatja a választ. 2016 őszi félévében azt találta ki, hogy a megtanulandó anyagot jegyzet formájában hétről hétre a hallgatók rendelkezésére bocsájtja. A hallgatókat megkérte arra, hogy az órák előtt olvassák el a kiadott anyagot. A módszer megteremtette az elvi lehetőségét annak, hogy ideális hallgatói kooperáció mellett több időt lehessen az anyag nehezebb részeinek átbeszélésével tölteni, illetve cél volt az is, hogy az átbeszélendő részek felosztásával csökkenjen az előadásnak és a gyakorlatnak a magyar felsőoktatási rendszerben nagyon markáns elkülönülése és az ezzel együttjáró „előadáskerülés”. Ez a hozzáállás a mostani járvány miatti nehéz időszakban különösen aktuális. A hallgatóknak szánt jegyzetet szemeszterről szemeszterre tökéletesítve megszületett az új, négykötetes valószínűségszámítás tankönyv.
A tankönyv részletes, szemléletes és közvetlen magyarázatokkal, rengeteg megértést segítő ábrával és táblázattal és meglehetősen sok kidolgozott nagyszerű feladattal igyekszik elérni azt, hogy az órákra való készülés ne kötelesség, hanem élmény legyen.
Az egyes kötetek alcímei:
1. Valószínűségek és diszkrét valószínűségi változók
2. Nevezetes diszkrét eloszlások
3. Egydimenziós folytonos valószínűségi változók
4. Folytonos eloszlások két dimenzióban
Az anyag többé-kevésbe a bevezető valószínűségszámítás kurzusokon megszokott sorrendet követi, azt leszámítva, hogy már az első kötetben előkerül a kétdimenziós diszkrét valószínűségi változó, a feltételes eloszlás, a konvolúció fogalma. Az említett fogalmak korai felbukkanása elmélyíti a valószínűségszámítás megértését, úgy, hogy definiálásukhoz a korábban bevezetett valószínűségszámítási fogalmak mellett mindössze az aritmetikai alapműveletekre van szükség. Megjegyzem, hogy az első kötet elején a szerző ajánl egy alternatív sorrendet is, amelyben a folytonos valószínűségi változók tárgyalása sokkal előbbre kerül.
Ahogy már utaltam is rá, a könnyű önálló tanulás egyik kulcsa a rengeteg kidolgozott nagyszerű feladat. A könyv hangulatát jól érzékelteti az alábbi két példa (a második egy hallgató kérdése nyomán jött létre). A megoldásokat a könyvben találja az olvasó.
„Egy erdőben ismeretlen számú szarvas él. A számuk becslése céljából 60 szarvast piros festékkel megjelölünk, majd néhány hét eltelte után megszámoljuk, hogy 40 véletlenszerűen választott szarvas között hány megjelöltre bukkanunk. Tegyük fel, hogy 15-re. Mit mondhatunk ezek alapján a szarvasok ismeretlen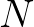 
számáról?”
„Mi lenne, ha az 5 forintos érmét is kivonnák a forgalomból? Nyilvánvaló, hogy a zöldséges számára kedvező lenne, ha fizetéskor az 5-re végződő számokat felkerekítenék, a vevő számára pedig az lenne kedvező, ha lekerekítenék. De vajon az ebből a kerekítésből adódó extra nyereségek is az elhanyagolható kategóriába esnek, vagy már nem?”
A könyv anyagának nem elhanyagolható része „Extra tananyag” megjelöléssel van ellátva. Ezek többnyire nem részei az A4 kurzus szokásos tananyagának, de érdeklődő hallgatóknak igazi ínyencségek. Például az extra anyagok között szerepel a nagy számok erős törvényének bizonyítása indikátor valószínűségi változókra, de a Borel–Cantelli-lemmák is feltűnnek az örök boldogság elérésének köntösében.
Az első kötet előszó helyett a hallgatóknak írt üzenettel kezdődik. Ebből kiderül, hogy András értékelési rendszerének része, hogy a vizsgát követően a hármasra vagy négyesre állók jobb jegyért megválaszolhatnak egy, az extra anyag általuk választott, ám megfelelően nagy részéhez kötődő kérdést. A hallgatók többnyire örömmel kihasználják ezt a lehetőséget.
A tankönyv, ahogy fent említettem, nem előzmény nélküli. [3] szimulációs világa beszűrődik a könyvbe. A nevezetes egy-, illetve kétdimenziós eloszlások mellett szerepelnek a számolást lehetővé tevő Excel-formulák, illetve a könyv több helyen megfelelő mennyiségű magyarázat mellett önálló Excel-szimuláció készítésére biztatja az olvasókat. A 2. kötet 37. oldalán van egy link az A4 tárgy egy korábbi honlapjára, ahol elég sok elkészült Excel-szimulációt talál az olvasó. Véleményem szerint a vegyes tartalomra mutató egyetlen link nem ideális. Az elektronikus tankönyvi forma lehetővé teszi az utólagos javításokat, illetve kiegészítéseket. Érdemes lenne több helyre tenni Excel-szimulációkra mutató linket.
A recenzió teljessége érdekében megjegyzem, hogy a könyvben maradt néhány sajtóhiba, illetve néhány további (belső) hivatkozással tovább lehetne növelni a tartalom kohézióját.
A könyv elolvasát minden valószínűségszámítást oktatónak és minden kellő háttértudással rendelkező, a valószínűségszámítást, illetve a ráépülő diszciplinákat (például az információelméletet és a statisztikát) mélyen érteni vágyó tanulónak nagyon ajánlom. Az első két kötethez jól jön, ha ismerjük a sorozatok és sorok alapfogalmait, de ennek hiányában is élvezetes olvasmány. A harmadik kötethez szükséges az egyváltozós függvények analízisének ismerete, a negyedik kötethez pedig a kétváltozós függvények analízise.
A BME és egyéb előfizető intézmények dolgozói illetve hallgatói ingyenesen olvashatják a könyv mind a négy kötetét a https://edu.interkonyv.hu oldalon.
A tankönyv recenziójának zárásaként jöjjön két videó. Az első videót tanszékünk külső óraadója, Kirsch Norbert készítette 2016-ban. Ebben András a hallgatók körében méltán népszerű kullancsos feladattal foglalkozik. A második videó egy friss online óra felvétele amelyben András, a Matematika A4 új előadójának, Keszthelyi Gabriellának a felkérésére Excel-szimulációkkal szemlélteti a folytonos eloszlásokat.
https://www.youtube.com/watch?v=hlGnwQmi6ic
A videókban látott oktatói stílus és szemléltetési módszerek visszaköszönnek a tankönyv hasábjain is.
Irodalomjegyzék
[1] Vetier András: Valószínűségszámítás, Tankönyvkiadó, 1981, https://math.bme.hu/~vetier/051360_Vetier_Valoszinusegszamitas.pdf
[2] Vetier András: Szemléletes mérték- és valószínűségelmélet, Tankönyvkiadó, 1991
[3] Vetier András: Probability theory with simulations, Typotex, 2011., https://edu.interkonyv.hu/book/2822-vetier_probability_theory_with_simulations
Kói Tamás adjunktus
BME Matematika Intézet, Sztochasztika Tanszék