Hibrid képalkotás és vizualizáció

Gépi tanulás alkalmazása Mathematica-val és Pythonnal

Joseph Awange, Béla Paláncz, Lajos Völgyesi: Hybrid Imaging and Visualization Employing Machine Learning with Mathematica – Python, Springer Nature Switzerland AG 2020

A számítógépes látás alapfeladata, hogy képekből valamilyen szempontok szerint releváns információt nyerjünk ki, például: található-e adott típusú objektum a képen, és ha igen, hol; mely pixelek tartoznak egy adott objektumhoz; a képen szereplő objektumok milyen nagyobb osztályokba, kategóriákba sorolhatók; vagy melyek egy kép fő jellegzetességei. A könyvben a szerzők a számítógépes látást gépi tanulási problémákként fogják fel; mivel pedig a gépi tanulásra statisztikai technikák alkalmazásaként gondolnak, ezért feltételezik a valószínűségszámítás alapvető elemeinek, jelöléseinek ismeretét. A szerzők szerint a tématerület könyvei általában két csoportra oszthatók: vagy főként elméleteket és tételeket tárgyalnak, vagy konkrét programozási gyakorlatokat. Jelen könyvüket ezért hiánypótló műnek szánják, amely mindkét megközelítést ötvözi.

A könyv öt fejezetből áll: dimenziócsökkentés, osztályozási módszerek, clustering technikák, regressziós technikák, illetve neurális hálózatok alkalmazása a számítógépes látásban. Minden fejezet számos módszert mutat be ugyanannak a problématípusnak a kezelésére. Az 1. fejezet például különféle (adatvesztéses) tömörítésekkel foglalkozik, többek között főkomponens-analízissel, szingulárisérték-felbontással, függetlenkomponens-analízissel, diszkrét Fourier-transzformációval, diszkrét wavelet-transzformációval, vagy fixponttételeken alapuló módszerekkel. Az egyes alfejezetek egy-egy nagyon rövid (általában 1-2 bekezdésnyi) elméleti összefoglalóval indulnak (nincs tehát részletes kifejtés vagy magyarázat), amit konkrét példák és programkódok ismertetése és részenkénti magyarázata követ. A szerzők hibrid programozási környezetet használnak: a programkódokat alapvetően Wolfram-nyelven (Mathematica-ban) írták, amikbe természetes módon ágyazhatók Python-kódrészletek (a Mathematica-ból a Python közvetlenül futtatható). A szerzők feltételezik, hogy az olvasó eleve ismeri ezt a két szoftvert. A bemenetet és kimenetet a 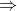és 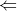szimbólumok jelzik (ezeket a jelöléseket a könyv elején esetleg lehetett volna definiálni). A programkódok, bemenő adatok, képek és a programok kimenetei általában teljes terjedelmükben szerepelnek – a 419 oldalból az angol nyelvű szöveg így viszonylag csak kis részt foglal el. Emiatt a hagyományos papíralapú, vagy PDF-alapú könyvformátumot kevésbé érzem hasznosnak: a könyvbeli információ interaktív dokumentumként (például interaktív Mathematica notebook formájában) lenne legkönnyebben használható. A fejezetek végén az aktuálisan tárgyalt módszereket összehasonlítják egymással, és gyakorlati szempontokból is elemzik őket. Az egyes fejezetek tehát összképet, tételes felsorolást adnak a lehetséges módszerekről és egymáshoz való viszonyukról – kedvcsinálóul azok számára, akik a további részletekről a (fejezeteket külön-külön lezáró) irodalomjegyzék alapján tájékozódnának.