2017 májusában Budapesten dr. Albert Rékát, a Pennsylvania State University professzorát több alkalommal is felkérték előadónak. Fiatalon, mint általános hálózatkutató, a Barabási—Albert modell megalkotásával hozzájárult a skálafüggetlen hálózatok elemzéséhez. Érdeklődése néhány éve a biológiai hálózatok dinamikája felé irányult, és elsők között alkalmazta rájuk a Boole-logikán alapuló leírást.
Az illusztráló képek a Rényi Intézet szemináriumán megtartott Biológiai hálózatok irányítása című kétrészes előadásából valók: A biológiai rendszerek funkciója rendszerszintű, emergens tulajdonság. Az ilyen rendszerek külső irányításához (modulálásához) is a rendszer egészét kell figyelembe venni. Sajnos a legtöbb rendszer esetében nincs elég információ egy részletes dinamikus modell parametrizálásához. Ezért nagy az érdeklődés a hálózatstruktúra-alapú kontroll módszerek iránt. Ez az előadás három ilyen módszert hasonlított össze. Albert Réka kutatócsoportja a Boole-dinamika esetén érvényes stabil motívum alapú kontrollt kutatja, amit sikerrel alkalmaztak jelátviteli hálózatok irányítására.
Az előadás után készült az alábbi interjú.
Mit érdemes tanulni annak, aki hálózatokkal szeretne foglalkozni?
Elsősorban gráfelméletet és hálózattudományt, amit úgy értelmeznék, mint a gráfelmélet új, alkalmazott, adatirányított ágát. Az is nagyon fontos, hogy megértse azt a szakterületet, aminek a hálózataival foglalkozni fog. Tudnia kell, hogy mik azok a kérdések, amelyek fontosak ezen a területen, és meg kell találnia, hogyan lehet ezeket a kérdéseket hálózat-feladatként megfogalmazni es végül megoldani. Sok esetben a szakterület sajátos hálózatai új gráf-fogalmakat igényelnek. Például az általam kutatott sejt-biológiai hálózatokban fontosak a negativ élek, és az élek közötti együttműködes és függőség.
A gráfelmélet maga is fiatal ága a matematikának, a belőle kiinduló, de attól teljesen eltérő hálózattudomány pedig még újabb. Barabási Albert-László nevéhez kötik a „felfedezését”, és azóta a világon több reál, humán vagy közgazdasági tudományterület kutatói jöttek arra rá, hogyan alkalmazható az ő kutatásaikban.
László erről sokat ír a hálózatokról szóló könyveiben, mindkettő nagyon érdekes olvasmány: a Behálózva - A hálózatok új tudománya általános ismeretterjesztő, http://ematlap.hu/index.php/konyvespolc-2017-06/516-barabasi-albert-laszlo-a-halozatok-tudomanyaA hálózatok tudománya tudományos szakkönyv. Nagyjából velünk egy időben Steven Strogatz és Duncan Watts is gondolkodott a hálózatokról. Úgy gondolták, hogy a rendszerek valahol a szabályos rácsok és a véletlen hálók között vannak. Az ő cikkük, ami a kisvilág modellt írja le, 1998-ban jelent meg, kevesebb mint egy évvel a mienk előtt. Mi akkor már szintén ezen a témán gondolkodtunk, és volt is már egy cikkünk, csak éreztük, hogy az még nem elég, így az ő publikációjuk még jobban inspirált bennünket a további munkára. A skálafüggetlen hálók és a Barabási—Albert modell fundamentálisan új volt, mert összekötötte a hálózat elemzését a hálózat dinamikájával. Azt mondta, hogy ha megértjük a hálózat dinamikus változását, és modellezzük azt, akkor meg fogjuk érteni a hálózat jelenlegi struktúráját, és meg tudjuk jósolni a jövőbeli struktúráját is. A két cikk együtt jelentette a nagy áttörést. Duncan Watts és László is nagyon aktívak voltak abban, hogy népszerűsítsék ezt a tudományt. Egyrészt nagyon sok fizikust inspirált a két cikk, másrészt sokan más területekről is megérezték a hálózatok alkalmazásának fontosságát.
Miben új, más a hálózatkutatás és milyen alkalmazási területe van?
A hálózatkutatás egyik újdonsága az, hogy utat mutat a komplex kölcsönható rendszerek megértése felé. A hagyományos módszerek (például redukcionizmus, vagy statisztikus fizika) nem igazán alkalmazhatók erre a célra, mert a komplex rendszerek nagyon heterogének es az emergens, rendszer-szintű tulajdonságaikat nem lehet egyedi elemekre, vagy átlagos tulajdonságokra visszavezetni. Az ilyen rendszerek megértésének első lépése, hogy hálózatként értelmezzük őket. A rendszer elemei a hálózat nódusaivá (csúcsaivá) válnak, a kölcsönhatásaik pedig élekké. A hálózat elemzése megmutatja a hálózat kapcsolatmintáit. Például megmutatja azokat a nódusokat, amelyeknek aránytalanul sok éle van, ezek nagy valószínűséggel fontos szerepet játszanak. Irányított hálózatok elemzése megadja a hálózat szorosan összefüggő komponenseit, vagyis olyan nódus-csoportokat, amelyek között sok visszacsatolás van, és amelyek dinamikája is valószínűleg összekapcsolódik.
Albert Réka honnan indult és hová jutott eddigi életében?
Szászrégenben születtem, Erdélyben, később Marosvásárhelyre költöztünk. Édesanyám, Barabás Sarolta, fizikatanárnő volt, most biogazda, édesapám, Barabás László, néprajzkutató, főiskolai docens. A gyerekkoromat a Ceausescu-diktatúra utolsó éveiben éltem, tizennyolc éves voltam a rendszerváltáskor. A matematika, fizika jelentette számomra azt a területet, ahol minden logikus, érthető volt, ahol meg tudtam oldani a problémákat. Kitűnő tanáraim voltak, általános iskolában Bató Domokos tanított matematikából es anyukám fizikából. A líceumban Dályai Pál tanította a matematikát, Tőkés András a fizikát. A kolozsvári Babes-Bolyai egyetem fizika szakán végeztem; Néda Zoltán, a szakdolgozati témavezetőm vezetett rá a kutatás izgalmas területére. Az egyetemen ismerkedtem meg Albert Istvánnal, aki technológiai fizika szakra járt, és akivel harmadévesen összeházasodtunk. A következő évben megszületett a fiunk, Ákos.
Mi voltunk az első évfolyam, amelyik mesterképzésre iratkozhatott be. Ez alatt az év alatt adódott egy fantasztikus továbbtanulási lehetőségünk. Barabási Albert-László ugyanis éppen akkor kezdett tanítani a Notre Dame egyetemen, es jó diákokat keresett. Néda Zoltán pedig engem es férjemet ajánlott neki. Letettük a vizsgákat es mindkettőnket felvettek Ph.D. hallgatónak, így költöztünk ki mindhárman Amerikába. A Ph.D. öt éve nagyon izgalmas, sűrű időszak volt, meghatározta életem további alakulását. László megismertetett a hálózattudománnyal, ami azóta is alapja a kutatásomnak. Férjemmel egymás utáni napokon védtük meg a disszertációinkat. Ezután két évig Minnesotában voltunk posztdoktori kutatók, majd megérkeztünk a Pennsylvania State Universityre. Azóta is ott tanítunk, kutatunk, most már tizennégy éve.
Azóta még egy kislányuk is van. Lehet egy nő egyszerre tudós és családanya?
Igen. Az kell hozzá, hogy ne legyenek maximalista elvárások egyik területen se. Egy tudósnak sem kell állandóan a kutatásán gondolkodnia. Az persze szükséges, hogy rendszeresen legyenek többórás megszakítás nélküli periódusok. Egy családanyának nem kell minden idejét a családjára fordítania, ha jó segítő-hálója van. Kulcsfontosságú, hogy a gyerekek napi foglalkozása jól meg legyen oldva, bölcsődében, óvodában, iskolában. Az is nagyon fontos, hogy a férj, családapa egyenlően részt vegyen a háztartásban, a családi feladatokban. Szervezés, rugalmasság, megértő rokonok, barátok, kollégák kellenek hozzá.
Hihetetlen érzés lehetett ilyen fiatalon, szinte véletlenül a tudományos pezsgés kellős közepébe csöppenni
Nagyon izgalmas, szép évek voltak. László a Notre Dame-os első tanítási évében felvett két diákot, az ő témájuk még nem hálózatkutatás volt. Én a második évében kerültem hozzá, én voltam az első, aki hálózatokkal kezdtem foglalkozni. Utánam jöttek aztán hárman, négyen, ők már mind hálózatokon dolgoztak. Nagyon ötletgazdag, pörgős kutatás volt, az egész csoportban nagyon nagy volt a lelkesedés, éreztem, hogy ez egy különleges kutatási téma.
Az én mostani kutatócsoportomban általában 3-4-en vannak, különböző területekről. Szeretem hogy általában a diákok keresnek meg engem: vagy egy fizikus azért jön, mert érdeklik a komplex rendszerek, vagy egy biológus rájön, hogy azon a szakterületen, ahol dolgozik, egy modellre van szükség, mert az egy hálózat-probléma. Ha ilyen motivált a diák, akkor nagyon jól megy a munka. Általában mindenkivel külön dolgozom a témáján, de elősegítem, hogy ők is találjanak egymással közös projekteket. Most például nálam egy fizikus és egy biológus együtt dolgozik: ugyanannak a problémának az egyszerűbb biológiai modellezését az egyikük végezte, ugyanakkor, amikor bonyolultabb modellre, új elméletre volt szükség, a másikuk tudott segíteni.
Ha bebizonyosodik egy feltevés egy biológiai modell esetén, ezután hogyan kerül sor a valódi alkalmazásra, amivel meg lehet állítani például a rák terjedését?
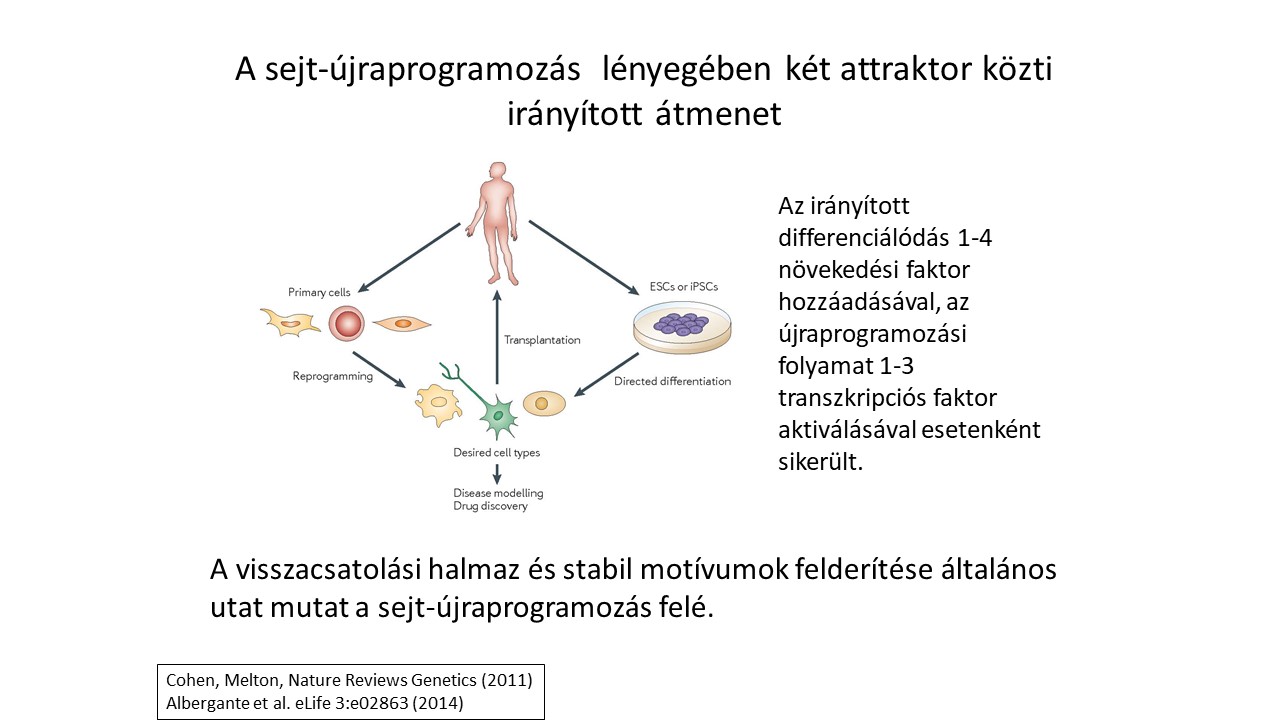Az első lépés a modell, a modell alapján tudunk feltételezéseket tenni, jósolni; ezeket a jóslatokat a kísérletileg ellenőrizzük. Ha például a jóslat egy lehetséges célzott rákterápia az első kísérletek általában rákos sejtvonalakban történnek. Ha itt igazolódik, működik, a következő lépés a kísérlet a háromdimenziós szövetekben, ami kicsit bonyolultabb. Utána lehet egérkísérleteket végezni, ha ez mind sikeres, akkor jönnek a klinikai vizsgálatok. Ez a folyamat hosszú-hosszú évekbe telik. Ez már nem ez én területem, de próbálok együttműködni orvos-kutatókkal, hogy közelebb maradjak a folyamathoz. Például, társ-témavezetője voltam egy nagyon tehetséges MD/PhD hallgatónak, aki most már orvos-kutató.
Széleskörűek a tudományos kapcsolatai?
Körülbelül tíz éve vannak Network Science konferenciák, az utóbbi években már évente kétszer is, ezek nagyon inspirálók. Másrészt ez egy óriási terület, lehetetlen elmenni mindenre, ezért én inkább a kisebb, biológiai hálózatokra fókuszáló konferenciákra járok. Magyarországról Csermely Péterrel (SOTE) tartom már 6 éve a kapcsolatot, ő hívott meg most is. Nagyon jó a hálózatkutatás a CEU-n is, Vedres Balázs vezetésével, és ott vannak Vicsek Tamás és kollégái az ELTÉ-ről, a RECENS kutatócsoport a MTA Társadalomtudományi Kutatóközpontjában, több csoport az MTA SZTAKI-n, a Rényi Intézetben.
Barabási évekkel ezelőtti előadásán zsúfolásig megtelt az előadóterem, olyanokkal is, akik talán először hallottak erről a témáról. Ebben az is benne volt, hogy a világhírű előadó magyar származású.
Jogosan büszkék a magyarok, hiszen valamikor Erdőssel, Rényivel és a gráfelmélettel kezdődött a mai hálózatkutatás.
Mit gondol a hálózattudomány jövőjéről? Most felszálló ágban van, meddig lehet eljutni?
Sokat fog még fejlődni, mert a rendszerek megkívánják a fejlődését. Ki kell találnunk új módszereket, fogalmakat; mi például kibővítjük a hálózatokat, stabil motívumokat keresünk. Szerintem sokat fog gazdagodni a hálózatok elmélete, és nyilván ki fognak bővülni az alkalmazási területek is.
Ez egy új látásmód. Egyre inkább felismerjük, hogy nagyon sok probléma hálózat-probléma, illetve ha hálózatként ábrázoljuk és hálózatként elemezzük, az előrevisz a megoldásában.
Korábban még nem volt elég járható út, de most már ott tartunk, hogy sok nemhomogén komplex rendszert is elemezni, jósolni tudunk. Most már a számítógépek is sokkal erősebbek, a módszerek is gazdagabbak. Megérett az idő erre a látásmódra minden tudományban, szükség van rá, ezért tovább fog fejlődni, bővülni, erősödni.
Köszönöm az interjút és azt is, hogy minden e-mailemre azonnal válaszolt: Oláh Vera.