Wiles professzor úr, engedje meg, hogy gratuláljunk a 2016-os Abel díj-elnyeréséhez. Őszintén szólva mi ketten arra számítottunk, hogy ez az interjú már évekkel ezelőtt megvalósul!
Ön nemcsak a matematikusok körében tett szert hírnévre, hanem a nagyközönség előtt is azzal, hogy az Abel-díjbizottságot idézve „bebizonyította a Fermat-sejtést az elliptikus görbékre vonatkozó Modularitási sejtés segítségével, és ezzel új korszakot nyitott a számelmélet történetében.” Ez a bizonyítás 1994-ben született, tehát több mint 20 évet kellett várnia az Abel-díj elnyerésére. Mindazonáltal eddig Ön a legfiatalabb díjazott az Abel-díjasok között.
Miután bebizonyította a Fermat-sejtést, nagyon sok interjút kellett adnia, ami most megnehezíti a mi dolgunkat. Hogyan fogunk olyan kérdéseket találni, amelyeket még nem válaszolt meg száz és száz alkalommal? Ígérjük, megteszünk minden tőlünk telhetőt.
A Fermat-sejtés — történeti áttekintés
A legelején kell kezdenünk, egy latin idézettel: „...nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere”, ami azt jelenti, hogy „nem lehet felosztani egy 2-nél magasabb hatványt két ugyanolyan hatvány összegére”. Azaz, a modern matematikai jelöléseket használva, az ![]() egyenletnek nincs megoldása a pozitív egészek körében ha
egyenletnek nincs megoldása a pozitív egészek körében ha ![]() . És az idézet így folytatódik „cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet”, ami azt jelenti, hogy „felfedeztem egy igazán gyönyörű bizonyítást erre, de ez a margó túl kicsi ahhoz, hogy ideférjen”. Ezt a megjegyzést 1637-ben írta Pierre de Fermat [1601—1655] francia jogász és amatőr matematikus Diofantosz Arithmetica című könyvének margójára. Biztosan nem számított rá, hogy ez a megjegyzés századokon át fogja izgalomban tartani a hivatásos és amatőr matematikusokat egyaránt, hogy megtalálják a bizonyítást.
. És az idézet így folytatódik „cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet”, ami azt jelenti, hogy „felfedeztem egy igazán gyönyörű bizonyítást erre, de ez a margó túl kicsi ahhoz, hogy ideférjen”. Ezt a megjegyzést 1637-ben írta Pierre de Fermat [1601—1655] francia jogász és amatőr matematikus Diofantosz Arithmetica című könyvének margójára. Biztosan nem számított rá, hogy ez a megjegyzés századokon át fogja izgalomban tartani a hivatásos és amatőr matematikusokat egyaránt, hogy megtalálják a bizonyítást.
Kérjük, röviden vázolja azokat a kísérleteket, amelyek a Fermat-sejtés bizonyítására születtek azelőtt, hogy Ön a sikeres módszerre rátalált volna. Továbbá, miért volt egy ilyen egyszerűnek tűnő kérdés ennyire vonzó, és a bizonyítási kísérletek miért voltak ekkora hatással a számelmélet fejlődésére?
 Az első komoly megoldási kísérleteket valószínűleg maga Fermat tette. Sajnos azonban ezekről semmi többet nem tudunk, mint amit ő maga leírt az
Az első komoly megoldási kísérleteket valószínűleg maga Fermat tette. Sajnos azonban ezekről semmi többet nem tudunk, mint amit ő maga leírt az ![]() és
és ![]() esetek bizonyításánál.1 Belátta, hogy egy köbszám nem bomlik két köb összegére, és egy negyedik hatvány nem bomlik két negyedik hatvány összegére. Ezt egy gyönyörű módszerrel bizonyította, amit azóta végtelen leszállásnak hívunk. Ez akkoriban új módszer volt a számelméletben, vagy legalábbis a bizonyításnak egy új nézőpontja. A módszert a kollégáihoz írt levelekben magyarázta el, illetve azon a bizonyos margón, már amennyi ráfért. Miután a margóra írt megjegyzéseket Fermat fia közzétette apja halála után, az egész dolog elfelejtődött egy darabig. Aztán Euler [1707—1783] felvette a fonalat, valamint mások is, akik megpróbálták megtalálni a csodálatos bizonyítást. És nem sikerült. A dolog meglehetősen drámaivá vált a 19. század közepére: több ember gondolta úgy, hogy megtalálta a megoldást. Volt erről egy vita a Francia Akadémián, ahol Lamé [1795—1870] azt állította, hogy megoldotta a problémát, és Cauchy [1789—1857] is ugyanezt állította magáról.
esetek bizonyításánál.1 Belátta, hogy egy köbszám nem bomlik két köb összegére, és egy negyedik hatvány nem bomlik két negyedik hatvány összegére. Ezt egy gyönyörű módszerrel bizonyította, amit azóta végtelen leszállásnak hívunk. Ez akkoriban új módszer volt a számelméletben, vagy legalábbis a bizonyításnak egy új nézőpontja. A módszert a kollégáihoz írt levelekben magyarázta el, illetve azon a bizonyos margón, már amennyi ráfért. Miután a margóra írt megjegyzéseket Fermat fia közzétette apja halála után, az egész dolog elfelejtődött egy darabig. Aztán Euler [1707—1783] felvette a fonalat, valamint mások is, akik megpróbálták megtalálni a csodálatos bizonyítást. És nem sikerült. A dolog meglehetősen drámaivá vált a 19. század közepére: több ember gondolta úgy, hogy megtalálta a megoldást. Volt erről egy vita a Francia Akadémián, ahol Lamé [1795—1870] azt állította, hogy megoldotta a problémát, és Cauchy [1789—1857] is ugyanezt állította magáról.
Valójában egy német matematikus, Kummer [1810—1893] addigra már írt egy cikket, amelyben elmagyarázta, hogy a probléma gyökere a számelmélet alaptételéhez nyúlik vissza. A természetes számok körében minden szám lényegében egyértelműen írható fel prímszámok szorzatára. Például 12 egyenlő 2-szer 2-szer 3. Nem lehet máshogy felbontani. De amikor a kutatók a Fermat-sejtést akarták bizonyítani, akkor olyan számrendszereket használtak, amelyben ez a felbontási egyértelműség nem igaz. Minden megoldási kísérlet azért fulladt kudarcba, mert ez a felbontási egyértelműség sérült. Kummer mindezt hihetetlen részletességgel elemezte. Gyönyörű eredményekkel állt elő, és végül sok speciális esetben belátta a Fermat-sejtést. Például, ![]() esetén minden prím kitevőre megoldotta a 37, 59 és 67 kivételével. Végülis azonban nem tudott általános megoldást adni. A módszere a Fermat-féle végtelen leszállás volt ezekben az új számrendszerekben.
esetén minden prím kitevőre megoldotta a 37, 59 és 67 kivételével. Végülis azonban nem tudott általános megoldást adni. A módszere a Fermat-féle végtelen leszállás volt ezekben az új számrendszerekben.
A Kummer által használt új számrendszerek vezettek az algebrai számelmélet mai formájának megszületéséhez. Az ember ezekkel a számokkal próbál egyenleteket megoldani ahelyett, hogy egész vagy racionális számokkal dolgozna. Ilyen irányú kísérletek még folytatódtak egy darabig, de aztán kifulladni látszottak a 20. századra. Senkinek sem volt alapvetően új ötlete. A 20. század második felére a számelmélet továbblépett más kérdések vizsgálatára, és a Fermat-sejtés szinte elfelejtődött a hivatásos matematikusok körében.
Aztán 1985-ben egy német matematikus, Gerhard Frey, egy váratlan új ötlettel állt elő: fogott egy feltételezett megoldást a Fermat-egyenletre, és egy átalakítás után nyert belőle egy úgynevezett elliptikus görbét. És megmutatta, vagy legalábbis utalt rá, hogy ennek az elliptikus görbének nagyon furcsa tulajdonságai vannak. Annyira furcsák, hogy azt sejtette, hogy ilyen görbék nem is létezhetnek. Frey ötletét fejlesztette tovább egy évvel később Kenneth Ribet amerikai matematikus, aki megmutatta, hogy a Fermat-egyenlet minden megoldása automatikusan ellenpéldát szolgáltatna egy másik jól ismert sejtésre is, a Modularitási sejtésre. Ezt a sejtést először Taniyama [1927—1958] fogalmazta meg egy gyengébb formában, majd később Shimura finomított rajta. A Modularitási sejtés igazságára vonatkozóan André Weil [1906—1998] szolgáltatta az első meggyőző érvet, aki lehetővé tette a sejtés részletes vizsgálatát. Ezután elég sok részleges bizonyítékot sikerült találni, amelyek mind azt mutatták, hogy a Modularitási sejtés valóban igaz. És emiatt a matematikusok azt látták, hogy „igen, a Fermat-sejtés is igaz kell, hogy legyen”. Sőt, kell, hogy legyen rá bizonyítás is.
Az történt ugyanis, hogy a Modularitási sejtés olyan jelentőségű probléma volt, hogy nem lehetett csakúgy félrerakni 500 évre. A modern matematika egyik központi sejtése volt. A Fermat-sejtés önmagában még elég marginális volt, és félre lehetett volna rakni akár örök időkre is, de a Modularitási sejtéssel már nem ez volt a helyzet. Tehát Ribet munkája után már láttam, hogy így talán meg lehet oldani a Fermat-sejtést, és azt is tudtam, hogy én meg fogom próbálni.
Térjünk vissza egy kicsit Fermat eredeti állítólagos bizonyítására. Gondolja, hogy Fermat ugyanazt az ötletet használta, mint Lamé, és hibásan azt feltételezte, hogy a megfelelő körosztási egészek között igaz az egyértelmű faktorizáció?
Nem, ezt nem hiszem, bár ez az ötlet is ott lehetett valahol. Nehéz ezt kinyomozni. André Weil írt erről: mindegyik másik probléma, amivel Fermat foglalkozott, 0 vagy 1 génuszú görbékkel volt kapcsolatban, és akkor most hirtelen egy magasabb génuszú görbét kezd vizsgálni. Vajon hogyan fog erről gondolkodni? Amikor tizenévesen megpróbálkoztam a sejtéssel, beleképzeltem magam Fermat helyébe, hiszen nem is nagyon tudtam mást tenni: képes voltam megérteni a 17. századi matematikát, de semmi annál sokkal mélyebbet. Úgy tűnt, hogy minden, amit Fermat csinált, végülis kvadratikus formákkal volt kapcsolatos, ezért úgy gondoltam, hogy talán ebből az irányból lehetne megközelíteni a sejtést. Persze nem jártam sikerrel, de nincs semmi, ami arra utalna, hogy Fermat az egyértelmű faktorizáció csapdájába esett volna. Sőt, a kvadratikus formák szemszögéből ő már tisztában volt azzal, hogy néha igaz az egyértelmű faktorizáció, és néha nem. Tehát már értette ezt a különbséget. Ezért alig hiszem, hogy ezt a hibát követte volna el.
André Weil „A számelmélet története Hammurapitól Legendre-ig” című könyvében, amelyre az előbb Ön is utalt, azt írja, hogy Fermat megvizsgálta az ![]() egyenletet, és belátta, hogy annak csak az
egyenletet, és belátta, hogy annak csak az ![]() és
és ![]() megoldása van. André Weil szerint Fermat ekkor a
megoldása van. André Weil szerint Fermat ekkor a ![]() gyűrűben dolgozott, amelyben igaz az egyértelmű faktorizáció.
gyűrűben dolgozott, amelyben igaz az egyértelmű faktorizáció.
Igen, Fermat használta az egyértelmű faktorizációt, de a kvadratikus formákon keresztül. És azt hiszem a ![]() gyűrűnek megfelelő kvadratikus formákat is vizsgált, ahol viszont nincs egyértelmű faktorizáció. Tehát szerintem értette a különbséget. Legalábbis nekem ez a benyomásom.
gyűrűnek megfelelő kvadratikus formákat is vizsgált, ahol viszont nincs egyértelmű faktorizáció. Tehát szerintem értette a különbséget. Legalábbis nekem ez a benyomásom.
Matematikai neveltetés
Úgy hírlik, hogy már kisgyerek korában érdekelték Önt a matematikai fejtörők. Honnan jött ez az érdeklődés? Volt valaki, aki hatással volt Önre?
Élveztem a matekot kisgyerek koromban. 10 éves koromban a könyvtárban a matematikai tárgyú könyveket nézegettem. Egyszercsak a kezembe akadt E. T. Bell [1883—1960]: „Az utolsó probléma” című könyve, amely már a borítóján tartalmazza a Fermat-egyenletet, és a probléma romantikus történetét. Teljesen magával ragadott a könyv.
Volt még más is Eric Temple Bell könyvében, ami megragadta a képzeletét?
Igazából az egész könyv a Fermat-egyenletről szól, és elég bőbeszédű. Kevesebb benne a matematika, mint gondolná az ember. Engem az egyenlet fogott meg. Aztán amikor rátaláltam erre az egyenletre, utána kikerestem más elemi matematika könyveket is számelméletről, tanultam kongruenciákról, és megnéztem egyéb dolgokat is, amiket Fermat csinált.
És mindezt a szokásos iskolai terhelés mellett?
Igen, az iskolát nem tartottam nagyon megterhelőnek, maradt mellette időm.
Már akkor világos volt az Ön számára, hogy kivételes tehetsége van a matematikához?
Az biztos, hogy volt matematikai tehetségem, és szerettem matekozni, de azt nem éreztem, hogy különleges lennék. Igazából nem is hiszem, hogy az voltam: az iskolámban sokan mások is jók voltak matekból, és vannak közülük, akik szintén matematikusok lettek.
Már ebben az életkorban is azt tervezte, hogy matematikát fog tanulni, és matematikusi életpályára megy?
Nem, mert akkor még nem értettem, hogy az ember akár az egész életét is a matematikára teheti fel. Ez csak később jött. De az biztos, hogy addig akartam matekot tanulni, ameddig csak lehet. Amennyi keveset előre láttam a jövőmbe, abban ott volt a matematika.
Oxfordban kezdte meg a matematikai tanulmányait 1971-ben. Kérjük, mondjon erről néhány szót. Voltak olyan tanárok vagy olyan szakterületek, amelyek nagyon meghatározóak voltak az Ön számára?
Mielőtt Oxfordba mentem volna, még középiskolában volt egy tanárom, akinek számelméletből volt PhD-je. Tőle kaptam egy példányt Hardy és Wright „Bevezetés a számelméletbe” című könyvéből, valamint találtam egyet Davenport „Magasabb aritmetika” című könyvéből is. Ez a két könyv nagyon inspiráló volt számomra számelméleti szempontból.
Tehát már Oxford előtt a pályára állították ezek a könyvek?
Igen, pályára álltam, a számelmélet felé fordultam. Sőt, úgy éreztem, hogy később az egyetem kissé megzavart ebben, hiszen csomó minden mást is kellett tanulnom: alkalmazott matematikát, logikát, és így tovább, pedig én csak számelméletet akartam tanulni. Az első évben egyáltalán nem is volt számelmélet, és igazából a harmadik évfolyam előtt nem is tudtam komolyan számelmélettel foglalkozni.
Tehát nem érdekelte Önt például a geometria annyira, mint az algebra és a számelmélet?
Elsősorban a számelmélet és az algebra érdekelt. Szívesen megtanultam a többi tárgyat is, de a legjobban a számelmélet izgatott. A tanáraim elintézték, hogy felvehessek extra kurzusokat számelméletből, de sajnos nem sok volt a kínálatban.
Egyszer elhatároztam, hogy a korábbi iskolai latintanulásomnak azzal vehetném hasznát, ha eredetiben olvasnám Fermat írásait, de ez végül túl nehéznek bizonyult. Még ha a latint meg is értettem, azokban az időkben még nem a mai algebrai jelöléseket használták, így igen nehéz volt eligazodnom.
Biztosan megkönnyebbülés volt, amikor végzett Oxfordban, és megkezdhette a tanulmányait immár tényleg csak számelméletben, John Coates témavezetésével Cambridge-ben.
Igen, az első évben több tárgyat is tanultam, aztán rátérhettem egy speciális cikk megírására. Amikor találkoztam John Coates-szal, és megkezdtem vele a kutatást, az csodálatos volt. Az egyetemi évek tanulásához, biflázásához képest a kutatás számomra csodálatos váltás volt.
Elliptikus görbék
John Coates terelte Önt az elliptikus görbék és az Iwasawa-elmélet felé?
Teljes mértékben. Volt néhány remek ötlete, és elég nagylelkű volt ahhoz, hogy megossza ezeket velem.
Elmondta neki, hogy Ön érdeklődik a Fermat-sejtés iránt?
Talán igen, nem emlékszem. De az volt a helyzet, hogy nem volt semmi új ötlet a témában a 19. század óta. A kutatók a régi ötleteket próbálták tovább finomítani, és igen, néha sikerült is egy-két finomítás. De nem úgy tűnt, hogy ezek valaha elvezetnek a teljes megoldáshoz. Túl nehéz volt abból az irányból megtalálni a megoldást.
Amikor elliptikus görbékkel kezdett foglalkozni John Coates hatására, akkor még nem sejtette, hogy ezek később döntő szerepet játszanak a Fermat sejtés megoldásában?
Nem, ez csak egy varázslatos véletlen, hogy így alakult. Az a furcsa, hogy Fermat munkásságában két dolog emelkedik ki, amikre máig emlékszünk: az elliptikus görbék, és a híres sejtése. Például az egyenlet, amit említett ![]() , ez is egy elliptikus görbe. És ez a két dolog végül egymásra talált a sejtés bizonyításában.
, ez is egy elliptikus görbe. És ez a két dolog végül egymásra talált a sejtés bizonyításában.
El tudná magyarázni, hogy mik is azok az elliptikus görbék, és mi a szerepük a számelméletben?
Egy számelméleti kutató számára az elliptikus görbék Fermat-val kezdődtek, olyan egyenletekkel ahol ![]() egyenlő az
egyenlő az ![]() -nek valamely racionális együtthatós harmadfokú polinomjával. A probléma az, hogyan találjuk meg egy ilyen egyenlet racionális megoldásait. Fermat a következőt vette észre: néha az ember kiindulhat egy vagy két megoldásból, és azokból generálhat végtelen sok új megoldást. Néha viszont egyáltalán nincs megoldás. Ez a helyzet például a Fermat-sejtésnél
-nek valamely racionális együtthatós harmadfokú polinomjával. A probléma az, hogyan találjuk meg egy ilyen egyenlet racionális megoldásait. Fermat a következőt vette észre: néha az ember kiindulhat egy vagy két megoldásból, és azokból generálhat végtelen sok új megoldást. Néha viszont egyáltalán nincs megoldás. Ez a helyzet például a Fermat-sejtésnél ![]() -ra, ami valójában álcázott formában egy elliptikus görbe egyenletére vezet. Néha meg lehet mutatni, hogy nincs racionális megoldás. Szóval néha végtelen sok van, néha pedig egy sem. Ezt már Fermat is látta.
-ra, ami valójában álcázott formában egy elliptikus görbe egyenletére vezet. Néha meg lehet mutatni, hogy nincs racionális megoldás. Szóval néha végtelen sok van, néha pedig egy sem. Ezt már Fermat is látta.
A 19. században elkezdték ezeket az egyenleteket a komplex számok körében vizsgálni. Abel [1802—1829] maga is tanulmányozta az elliptikus függvényeket és a kapcsolatukat az elliptikus görbékkel, és megállapította, hogy az elliptikus görbéknek van egy csoport-struktúrája. Mindezeket már a 19. században jól értették a kétszeresen periodikus függvényekkel kapcsolatban. De ez a komplex megoldások elmélete.
Az egyenletek valós racionális megoldásait Poincaré [1854—1912] tanulmányozta. Amit most már Mordell-Weil tétel néven ismerünk, azt Mordell [1888—1972] bizonyította, majd aztán Weil az 1920-as években, megválaszolva ezzel Poincaré egy kérdését. A mi formalizmusunkban ez a tétel azt mondja, hogy a ![]() -racionális pontok egy elliptikus görbén egy
-racionális pontok egy elliptikus görbén egy ![]() számtest felett, tehát speciálisan
számtest felett, tehát speciálisan ![]() akár a racionális számok teste is lehet, egy végesen generált Abel-csoportot alkotnak. Azaz, Fermat nyelvén szólva, foghatunk véges sok megoldást, és azokból aztán az összes megoldás megtalálható a húr-érintő módszer segítségével.
akár a racionális számok teste is lehet, egy végesen generált Abel-csoportot alkotnak. Azaz, Fermat nyelvén szólva, foghatunk véges sok megoldást, és azokból aztán az összes megoldás megtalálható a húr-érintő módszer segítségével.
Birch és Swinnerton-Dyer, valamint Tate—Safarevics és Selmer...
Tehát sikerült megérteni a megoldások struktúráját, ami egy gyönyörű algebrai struktúra, egy csoport struktúra, csak éppen ez nem segít a konkrét megoldások megtalálásában. Senkinek sem voltak módszerei a megoldások megtalálására az 1960-as évekig, a Birch—Swinnerton-Dyer-sejtés felbukkanásáig. Két oldala van a dolognak. Az egyik analitikus, míg a másik pedig az úgynevezett Tate —Safarevics csoporthoz kapcsolódik. Lényegében a Tate—Safarevics-csoport adja meg a megoldási algoritmus megtalálásának obstrukcióit. És a Birch—Swinnerton-Dyer-sejtés azt mondja, hogy van egy analitikus módszer a Tate—Safarevics-csoport tanulmányozására. Ha mindezt összerakja az ember, akkor végeredményben kap egy algoritmust a megoldások megtalálására.
Ön már dolgozott a Birch—Swinnerton-Dyer-sejtésen a posztgraduális képzésekor John Coates-szal, ugye?
Igen, pontosan ezt a témát javasolta nekem Coates. Sikerült is az első eredményeket belátnunk erről az analitikus kapcsolatról az elliptikus görbéknek egy speciális osztályára.
Ezek voltak azok a görbék, amelyeken a komplex szorzás értelmezhető?
Igen, pontosan, amelyeken a komplex szorzás értelmezhető.
Ez volt az első általános eredmény a Birch—Swinnerton-Dyer-sejtéssel kapcsolatban?
Az első olyan, ami a görbéknek egy egész családjára vonatkozik, nem pedig egy-egy speciális görbére. Sok numerikus adat volt egy-egy görbére, de ez volt az első eredmény, ami görbéknek egy végtelen családját kezelte.
Mindez a racionális számtest felett, ugye?
Igen.
Meg kell említenünk, hogy a Birch—Swinnerton-Dyer-sejtés egyike a Clay Milleniumi Díj Problémáknak, azaz ha valaki megoldja, 1 millió dollárral jutalmazzák.
Igen, így van. Azt hiszem ez egy vonzó probléma, mert a gyökerei Fermat-hoz nyúlnak vissza. Ez is egy olyan elemien megfogalmazható probléma, ami egyenletekkel kapcsolatos, ezúttal alacsony fokú egyenletekkel, amelyekkel nem boldogulunk, és amelyeket még Fermat kezdett vizsgálni. Nagyon vonzó problémának találom.
Úgy gondolja, hogy megvannak már az eszközök a megoldásához? Ha valaki elég bátor, annak sikerülhet? Vagy kell még várnunk 300 évet a megoldás megszületésére?
Nem hiszem, hogy 300 évet kéne várnunk, de azt sem gondolom, hogy ez a legkönnyebb a milleniumi problémák közül. Azt hiszem, valami még hiányzik a megoldáshoz. Hogy minden eszköz megvan-e már, nem tudom. Talán igen. De mindig ott vannak ezek a spekulációk az igazán nehéz problémákkal kapcsolatban: talán még nincsenek is meg hozzá az eszközeink.
Nem hiszem, hogy bárki megoldhatta volna a Fermat-sejtést a 19. században, legalábbis azon az úton biztosan nem, ahogy végül a megoldás most megszületett. Túl nagy volt még a hézag matematikatörténeti szempontból: kellett várni 100 évet, mire a megfelelő eszközök megszülettek. Igazából sosem tudhatja az ember ezekkel a híres problémákkal, hogy vajon hozzáférhetők-e már az adott kor eszközeivel. Ezért is akkora kihívás a megoldásuk: ha az ember tudná, hogy mit lehet megoldani a mai eszközökkel és mit nem, már pusztán ez is egy óriási lépés lenne a megoldás felé!
Említette a Tate—Safarevics-csoportot, és ezzel kapcsolatban felmerül a Selmer-csoport is. Selmer [1920—2006] norvég matematikus volt, és Cassels [1922—2015] nevezte el róla a Selmer-csoportot. Tudna mondani pár szót a Selmer-csoportról, és hogy hogyan kapcsolódik ez a Tate—Shafarevich-csoporthoz, még akkor is ha a részletek kissé technikaiak?
Igen a részletek elég technikaiak, de azért valószínűleg el tudom magyarázni a Selmer-csoport mögötti ötletet. Egy elliptikus görbén keressük a racionális megoldásokat. A módszer az, hogy ha van már néhány megoldásunk, akkor azok segítségével testbővítéseket csinálunk. Ezt úgy csináljuk, hogy bizonyos gyököket vonunk a görbén lévő pontokból — mint ahogy vehetjük például a számok között az 5-nek az ![]() -edik gyökét vagy a 2-nek a köbgyökét. Hasonlóan, egy elliptikus görbén lévő pontnak is vehetjük az
-edik gyökét vagy a 2-nek a köbgyökét. Hasonlóan, egy elliptikus görbén lévő pontnak is vehetjük az ![]() -edik gyökeit. Ezek azok a pontok, amiket ha n-szer összeadunk (szorzás helyett), akkor visszakapjuk az eredeti pontot. Ezeknek a gyököknek a koordinátái aztán testbővítéseket generálnak, a mi esetünkben a racionális test bővítéseit.
-edik gyökeit. Ezek azok a pontok, amiket ha n-szer összeadunk (szorzás helyett), akkor visszakapjuk az eredeti pontot. Ezeknek a gyököknek a koordinátái aztán testbővítéseket generálnak, a mi esetünkben a racionális test bővítéseit.
Elég sok megszorítás tehető ezekre a testbővítésekre. És a Selmer-csoport lényegében a testbővítéseknek a legszűkebb halmaza, miután az ember a nyilvánvaló megszorításokat már feltételezte.
Összefoglalom még egyszer. Van a görbén lévő pontok csoportja. Ezek generálnak testbővítéseket (a gyökökön keresztül). De túl sok ilyen testbővítés van, nem akarjuk mindegyiket megengedni. Ezért lokális feltételekkel (![]() -adikus számokat használva) megszorításokat teszünk, amennyire csak lehet, és az így kapott testbővítések alkotják a Selmer-csoportot. És a görbén lévő pontok csoportja és a Selmer csoport közötti eltérést határozza meg a Tate—Safarevics csoport. Tehát bizonyos értelemben a Tate—Safarevics csoport adja meg a „hibatagot” amikor az ember a Selmer-csoportból akar következtetni a görbén lévő pontok csoportjára.
-adikus számokat használva) megszorításokat teszünk, amennyire csak lehet, és az így kapott testbővítések alkotják a Selmer-csoportot. És a görbén lévő pontok csoportja és a Selmer csoport közötti eltérést határozza meg a Tate—Safarevics csoport. Tehát bizonyos értelemben a Tate—Safarevics csoport adja meg a „hibatagot” amikor az ember a Selmer-csoportból akar következtetni a görbén lévő pontok csoportjára.
Selmer cikke, amelyre Cassels hivatkozik, a ![]() egyenlettel foglalkozik, és hasonló egyenletekkel. Selmer belátta, hogy ennek csak a triviális megoldása van az egészek között, de minden
egyenlettel foglalkozik, és hasonló egyenletekkel. Selmer belátta, hogy ennek csak a triviális megoldása van az egészek között, de minden ![]() -re van nem-triviális megoldása modulo
-re van nem-triviális megoldása modulo ![]() . Tehát ezen a görbén nincsenek racionális pontok. Miért nevezte el Cassels Selmerről a felmerülő csoportot az általános esetben?
. Tehát ezen a görbén nincsenek racionális pontok. Miért nevezte el Cassels Selmerről a felmerülő csoportot az általános esetben?
Valóban, ezek között elég finom kapcsolat van. Mi is a helyzet, ha egy elliptikus görbét tekintünk, ami ebben az esetben ![]() lenne? Ez egy nem szokványos módon megadott elliptikus görbe, és a Tate—Safarevics-csoporthoz más hasonlókat is tekintenünk kell, mint például a
lenne? Ez egy nem szokványos módon megadott elliptikus görbe, és a Tate—Safarevics-csoporthoz más hasonlókat is tekintenünk kell, mint például a ![]() görbét, mely szinten 1 génuszú gorbe, de ez utóbbinak nincs racionális pontja. Ennek Jacobi-varietása az eredeti
görbét, mely szinten 1 génuszú gorbe, de ez utóbbinak nincs racionális pontja. Ennek Jacobi-varietása az eredeti ![]() elliptikus görbe. A Tate—Safarevics-csoport egy leirási módja épp ilyen, racionális ponttal nem rendelkező elliptikus görbekkel lehetséges. Ezeket valahogy összerakva kapható meg a Tate—Safarevics-csoport, és ez az összerakás tükröződik vissza a Selmer-csoportban. Kicsit bonyolult ahhoz, hogy szavakban röviden elmagyárazzuk. Jómagam egy sokkal aritmetikaibb leírást adtam erre modulusbővítések alkalmazásával. Az inkább geometriai leírás pedig ezen csavart formák segítségével tehető meg.
elliptikus görbe. A Tate—Safarevics-csoport egy leirási módja épp ilyen, racionális ponttal nem rendelkező elliptikus görbekkel lehetséges. Ezeket valahogy összerakva kapható meg a Tate—Safarevics-csoport, és ez az összerakás tükröződik vissza a Selmer-csoportban. Kicsit bonyolult ahhoz, hogy szavakban röviden elmagyárazzuk. Jómagam egy sokkal aritmetikaibb leírást adtam erre modulusbővítések alkalmazásával. Az inkább geometriai leírás pedig ezen csavart formák segítségével tehető meg.
A Modularitási sejtés
Végeredményben Ön a Modularitási sejtés egy speciális esetét bizonyította be. Ahhoz, hogy ezt megértsük, először is a moduláris formákkal kell kezdenünk, valamint azzal, hogy mi közük van ezeknek az elliptikus görbékhez. El tudná ezt magyarázni?
Igen. Az elliptikus görbéket (a racionális test felett) egy ![]() alakú egyenlet adja meg, ahol
alakú egyenlet adja meg, ahol ![]() és
és ![]() racionális számok. (Továbbá van egy olyan feltétel is, hogy ne tűnjön el a diszkrimináns.) Ahogy elmondtam, már a 19. század elején leírást tudtak adni ennek az egyenletnek a komplex megoldásairól. Ezeket jól le lehet írni a Weierstrass-féle
racionális számok. (Továbbá van egy olyan feltétel is, hogy ne tűnjön el a diszkrimináns.) Ahogy elmondtam, már a 19. század elején leírást tudtak adni ennek az egyenletnek a komplex megoldásairól. Ezeket jól le lehet írni a Weierstrass-féle ![]() -függvénnyel, egy speciális elliptikus függvénnyel. Azonban ezzel csak a komplex struktúrát lehet látni, és nekünk pedig valahogy azt kéne megfogni, hogy
-függvénnyel, egy speciális elliptikus függvénnyel. Azonban ezzel csak a komplex struktúrát lehet látni, és nekünk pedig valahogy azt kéne megfogni, hogy ![]() és
és ![]() racionális számok, és a racionális elliptikus görbékről leírást adni.
racionális számok, és a racionális elliptikus görbékről leírást adni.
És ehhez a moduláris formák vagy moduláris görbék lesznek segítségünkre. Először néhány szót a moduláris függvényekről: ahhoz hozzá vagyunk szokva, hogy bizonyos függvények invariánsak egy eltolásra nézve. Például, amikor Fourier-sorokat használunk, akkor olyan függvényekkel dolgozunk, amik periodikusak, azaz invariánsak a periódussal való eltolásra nézve. A moduláris függvények olyan komplex függvények, amelyek invariánsak egy nagyobb csoport hatására nézve (általában az ![]() egy részcsoportjára nézve). Tehát egy a felső félsíkon értelmezett
egy részcsoportjára nézve). Tehát egy a felső félsíkon értelmezett ![]() komplex változós függvénytől megköveteljük, hogy
komplex változós függvénytől megköveteljük, hogy ![]() egyenlő legyen
egyenlő legyen ![]() -vel (vagy általánosabban megengedhetünk egy
-vel (vagy általánosabban megengedhetünk egy ![]() hatványával való szorzást).
hatványával való szorzást).
Ezek a moduláris függvények, és ezeket már behatóan tanulmányozták a 19. században. Meglepő lehet, de ezek adják a kulcsot az elliptikus görbék aritmetikájának tanulmányozásához. Talán a legegyszerűbb úgy elmagyarázni, hogy mivel az ![]() csoport hat a
csoport hat a ![]() felső félsíkon (ahogy
felső félsíkon (ahogy ![]() átmegy
átmegy ![]() -be), ezért le tudjuk faktorizálni
-be), ezért le tudjuk faktorizálni ![]() -t ezzel a hatással. És a faktor természetesen örökli egy racionálisok feletti görbe struktúráját.
-t ezzel a hatással. És a faktor természetesen örökli egy racionálisok feletti görbe struktúráját.
Ha vesszük ![]() -nek azt az úgynevezett kongruencia részcsoportját, ahol
-nek azt az úgynevezett kongruencia részcsoportját, ahol ![]() osztható egy
osztható egy ![]() számmal, akkor a kapott görbét
számmal, akkor a kapott görbét ![]() -szintű moduláris görbének hívjuk. A Modularitási sejtés azt mondja ki, hogy minden elliptikus görbe a racionálisok felett megkapható úgy, mint valamely
-szintű moduláris görbének hívjuk. A Modularitási sejtés azt mondja ki, hogy minden elliptikus görbe a racionálisok felett megkapható úgy, mint valamely ![]() -szintű modularitási görbe egy faktora. Ezzel az elliptikus görbéknek egy uniformizálást nyerjük a moduláris görbék által. Elsőre úgy tűnhet, hogy ezzel rajtavesztünk, hiszen az utóbbi egy magasabb génuszú görbe, tehát bonyolultabb. De valójában sokkal több struktúrája van.
-szintű modularitási görbe egy faktora. Ezzel az elliptikus görbéknek egy uniformizálást nyerjük a moduláris görbék által. Elsőre úgy tűnhet, hogy ezzel rajtavesztünk, hiszen az utóbbi egy magasabb génuszú görbe, tehát bonyolultabb. De valójában sokkal több struktúrája van.
És mindez egy nagyon erős eszközt ad a kezünkbe?
Igen, egy nagyon erős eszközt. Rendelkezésünkre állnak függvénytani módszerek, a deformáció elmélet, geometriai módszerek, stb. Sok-sok eszközünk van a tanulmányozásukra.
Taniyama, a fiatal japán matematikus, aki először észrevette ezeket az összefüggéseket, még ennél sokkal bizonytalanabb formában fogalmazta meg a sejtést, igaz?
Igen, az ő sejtése még nem volt ennyire pontosan megfogalmazva. Nem a modularitási csoportot használta az invarianciához. Már nem emlékszem pontosan, hogy mi is volt az ő sejtése, de az invariancia még valami másik csoportból származott. Nem volt ennyire pontosan kimondva, hogy a moduláris csoport kongruencia részcsoportjairól van szó. És eredetileg japánul volt írva, ezért nem kapott akkora nyilvánosságot, amelyet megérdemelt volna. Azt hiszem, egy Japánban lezajlott konferencia utáni kiadványban szerepelt.
Ez egy nagyon vakmerő sejtés volt abban az időben, ugye?
Igen, mindenképpen.
De aztán lassan a matematikusok felfigyeltek erre a sejtésre. Már említette, hogy Gerhard Frey a Fermat-sejtést összekötötte a Modularitási sejtéssel.
Igen. Gerhard Frey megmutatta, hogy ha a Fermat-egyenletnek van egy ![]() megoldása, és tekintjük az
megoldása, és tekintjük az ![]() elliptikus görbét, akkor ennek a görbének a diszkriminánsa egy teljes
elliptikus görbét, akkor ennek a görbének a diszkriminánsa egy teljes ![]() -edik hatvány lenne. És ha meggondoljuk, hogy mit jelent ez a Modularitási sejtést feltételezve (igazából egy kicsit erősebbet is fel kell tennünk: a Serre-féle epszilon-sejtést), akkor azt látjuk, hogy ez a görbe csak
-edik hatvány lenne. És ha meggondoljuk, hogy mit jelent ez a Modularitási sejtést feltételezve (igazából egy kicsit erősebbet is fel kell tennünk: a Serre-féle epszilon-sejtést), akkor azt látjuk, hogy ez a görbe csak ![]() -szintű lehet, és így a hozzá tartozó kongruencia részcsoport az maga
-szintű lehet, és így a hozzá tartozó kongruencia részcsoport az maga ![]() . De ha
. De ha ![]() -t lefaktorizáljuk
-t lefaktorizáljuk ![]() -vel, akkor egy nulla génuszú görbét kapunk, aminek nincsenek elliptikus görbe faktorai. Ezért tehát a Fermat-egyenletnek sem lehet megoldása.
-vel, akkor egy nulla génuszú görbét kapunk, aminek nincsenek elliptikus görbe faktorai. Ezért tehát a Fermat-egyenletnek sem lehet megoldása.
Az interjú folytatását 2017. szeptemberi számunkban közöljük. Következik: A megoldás nyomában.
Az interjút készítették: Martin Raussen (Aalborg University, Dánia), és Christian Skau (Norwegian University of Science and Technology, Norvégia). Fordította: Matolcsi Máté.
Az eredeti cikk az Európai Matematikai Társulat EMS Newsletters 2016. szeptemberi számában jelent meg: Interview with Abel Lauereate Sir Andrew Wiles, EMS Newsletter September 2016, p. 29—38. http://www.ems-ph.org/journals/newsletter/pdf/2016-09-101.pdf#page=31
Ezúton is köszönjük az EMS, a szerzők és Wiles professzor szíves engedélyét a fordítás megjelentetéséhez.
A Wilesról készült fénykép forrása a Wikimedia Commons:
https://commons.wikimedia.org/wiki/Category:Andrew_Wiles#/media/File:Andrew_wiles1.jpg copyright C. J. Mozzochi, Princeton N.J
Fermat képe: https://hu.wikipedia.org/wiki/Pierre_de_Fermat
Lábjegyzet
- 1
- Szigorúan véve először Euler adott teljes bizonyítást az
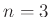 esetre.
esetre.









