A Maass-formák – vagy általánosabban az automorf formák – harmonikus hullámok, amelyek speciális szimmetriákkal rendelkeznek. A hullámok hagyományosan a fizikusokat érdeklik, de mivel a szóban forgó szimmetriák az egész számokból származnak, ezért a Maass-formákat elsősorban a számelmélészek kutatják. Kevésbé nyilvánvaló, hogy a Maass-formák nagyon hasznosak az egész számok megértésében, de a matematika egyéb területein is, pl. a matematikai fizikában. A segítségükkel mély összefüggéseket sikerült feltárni és nehéz kérdéseket sikerült megválaszolni. A matematika több híres megoldatlan problémája – pl. a Ramanujan-Selberg-sejtés, a Langlands-program, vagy az általános Riemann-sejtés – hozható kapcsolatba a Maass-formákkal.
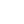
A Maass-formákat Hans Maass fedezte fel 1946-ban meglehetősen indirekt módon, számelméleti ![]() -függvényeken keresztül. A legegyszerűbb
-függvényeken keresztül. A legegyszerűbb ![]() -függvény a Riemann-féle zeta-függvény, amit az
-függvény a Riemann-féle zeta-függvény, amit az ![]() -nél nagyobb valós részű komplex számokon a
-nél nagyobb valós részű komplex számokon a
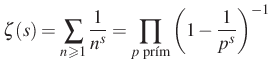
Dirichlet-sor, illetve Euler-szorzat definiál. A klasszikus gamma-függvénnyel kiegészített
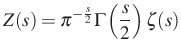
teljes zeta-függvény holomorfan kiterjed a ![]() pontozott komplex számsíkra, ahol kielégíti a
pontozott komplex számsíkra, ahol kielégíti a ![]() függvényegyenletet. Ennek a függvénynek a segítségével jól becsülhető a prímek száma egy adott korlátig, és az ilyen irányú vizsgálatok vezethették Riemannt a híres sejtésének megfogalmazásához: ha
függvényegyenletet. Ennek a függvénynek a segítségével jól becsülhető a prímek száma egy adott korlátig, és az ilyen irányú vizsgálatok vezethették Riemannt a híres sejtésének megfogalmazásához: ha ![]() , akkor
, akkor ![]() valós része
valós része ![]() . Az általánosabb, ún.
. Az általánosabb, ún. ![]() -ed fokú
-ed fokú ![]() -függvények Dirichlet-sorában az együtthatókat nem a konstans
-függvények Dirichlet-sorában az együtthatókat nem a konstans ![]() függvény adja meg, hanem egy általánosabb multiplikatív függvény; az Euler-szorzatban a
függvény adja meg, hanem egy általánosabb multiplikatív függvény; az Euler-szorzatban a ![]() prímhez nem az
prímhez nem az ![]() tényező tartozik, hanem a
tényező tartozik, hanem a ![]() egy legfeljebb
egy legfeljebb ![]() -ed fokú polinomja (amelyben az együtthatók csak a
-ed fokú polinomja (amelyben az együtthatók csak a ![]() -től függnek és a konstans tag mindig
-től függnek és a konstans tag mindig ![]() ); a teljes
); a teljes ![]() -függvényben szereplő extra tényező pedig nem a
-függvényben szereplő extra tényező pedig nem a ![]() , hanem ennek
, hanem ennek ![]() darab eltolt példánya. A függvényegyenlet az
darab eltolt példánya. A függvényegyenlet az ![]() alakot ölti, ahol
alakot ölti, ahol ![]() és
és ![]() egy pozitív egész (aminek prímosztóihoz tartoznak a
egy pozitív egész (aminek prímosztóihoz tartoznak a ![]() -nél kisebb fokú Euler-tényezők). Persze csak nagyon speciális multiplikatív függvény Dirichlet-sora rendelkezhet ilyen szép tulajdonságokkal, és ma már úgy gondoljuk, hogy minden ilyen függvény automorf eredetű.
-nél kisebb fokú Euler-tényezők). Persze csak nagyon speciális multiplikatív függvény Dirichlet-sora rendelkezhet ilyen szép tulajdonságokkal, és ma már úgy gondoljuk, hogy minden ilyen függvény automorf eredetű.
A prímszámok finomabb eloszlása motiválja az általánosabb ![]() -függvények bevezetését. Pl. ha arra vagyunk kíváncsiak, hogy egy adott korlátig hány prímszám ad
-függvények bevezetését. Pl. ha arra vagyunk kíváncsiak, hogy egy adott korlátig hány prímszám ad ![]() , illetve
, illetve ![]() maradékot
maradékot ![]() -gyel osztva, akkor a
-gyel osztva, akkor a ![]() mellett azt a Dirichlet-sort célszerű vizsgálni, amelyben az együtthatók
mellett azt a Dirichlet-sort célszerű vizsgálni, amelyben az együtthatók ![]() -esével ismétlődve rendre az
-esével ismétlődve rendre az ![]() értékek (mindkét
értékek (mindkét ![]() -függvény foka
-függvény foka ![]() ). Ily módon kiderül, hogy a kétféle maradék nagyjából egyenletesen oszlik el a prímek között. Továbbmenve, az
). Ily módon kiderül, hogy a kétféle maradék nagyjából egyenletesen oszlik el a prímek között. Továbbmenve, az ![]() maradékot adó prímszámok egyértelműen előállnak két négyzetszám összegeként, és ha arra vagyunk kíváncsiak, a két négyzetszám hányadosa az esetek hányad részében esik mondjuk
maradékot adó prímszámok egyértelműen előállnak két négyzetszám összegeként, és ha arra vagyunk kíváncsiak, a két négyzetszám hányadosa az esetek hányad részében esik mondjuk ![]() és
és ![]() közé, akkor a
közé, akkor a ![]() komplex másodfokú számtest bizonyos Hecke
komplex másodfokú számtest bizonyos Hecke ![]() -függvényeit célszerű vizsgálni (amelyek foka
-függvényeit célszerű vizsgálni (amelyek foka ![]() ). Ez utóbbi
). Ez utóbbi ![]() -függvényeket Hecke 1936-ban az akkoriban már jól ismert moduláris formákhoz tudta kapcsolni: megmutatta, hogy a Dirichlet-együtthatók megegyeznek egy alkalmas moduláris forma Hecke-sajátértékeivel. Maass 10 évvel később felismerte, hogy hasonló leírás létezik a valós másodfokú számtestek – mint pl. a
-függvényeket Hecke 1936-ban az akkoriban már jól ismert moduláris formákhoz tudta kapcsolni: megmutatta, hogy a Dirichlet-együtthatók megegyeznek egy alkalmas moduláris forma Hecke-sajátértékeivel. Maass 10 évvel később felismerte, hogy hasonló leírás létezik a valós másodfokú számtestek – mint pl. a ![]() – Hecke
– Hecke ![]() -függvényeire is, csak az ő esetükben moduláris formák helyett Maass-formákat kell tekinteni.
-függvényeire is, csak az ő esetükben moduláris formák helyett Maass-formákat kell tekinteni.
Mi is tehát egy Maass-forma? A Bolyai-féle hiperbolikus síkgeometria egyik ismert modellje a komplex számsík valós tengely feletti félsíkja. Ebben a modellben az egyenesek a valós tengelyt merőlegesen metsző egyenesek és félkörök. Az ![]() csoport minden eleme meghatároz egy irányítástartó egybevágóságot az alábbi törtlineáris hatással:
csoport minden eleme meghatároz egy irányítástartó egybevágóságot az alábbi törtlineáris hatással:
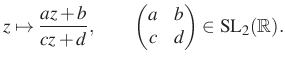
Valójában minden irányítástartó egybevágóságot megkapunk így. Tekintsük most az ![]() egy aritmetikus részcsoportját, példának okáért az
egy aritmetikus részcsoportját, példának okáért az ![]() -t. Maass-formán (pontosabban
-t. Maass-formán (pontosabban ![]() szintű és 0 súlyú Maass-formán) a
szintű és 0 súlyú Maass-formán) a ![]() felső félsík olyan korlátos (de nem konstans) függvényét értjük, ami invariáns az
felső félsík olyan korlátos (de nem konstans) függvényét értjük, ami invariáns az ![]() hatására nézve, továbbá sajátfüggvénye a
hatására nézve, továbbá sajátfüggvénye a
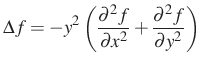
pozitív hiperbolikus Laplace-operátornak, tehát kielégíti a ![]() parciális differenciálegyenletet valamilyen
parciális differenciálegyenletet valamilyen ![]() konstanssal. Más szóval a Maass-forma az
konstanssal. Más szóval a Maass-forma az ![]() hiperbolikus felület korlátos (de nem konstans) Laplace-sajátfüggvénye. Persze cseppet sem világos, hogy ilyen egyáltalán létezik – a Maass által konkrétan megtalált formák csak az
hiperbolikus felület korlátos (de nem konstans) Laplace-sajátfüggvénye. Persze cseppet sem világos, hogy ilyen egyáltalán létezik – a Maass által konkrétan megtalált formák csak az ![]() egy véges indexű kongruencia-részcsoportjára voltak invariánsak. Mindenesetre Selberg a róla elnevezett nyomformulával 1956-ban belátta, hogy az általunk tekintett Maass-formák bőségesen léteznek, és az
egy véges indexű kongruencia-részcsoportjára voltak invariánsak. Mindenesetre Selberg a róla elnevezett nyomformulával 1956-ban belátta, hogy az általunk tekintett Maass-formák bőségesen léteznek, és az ![]() Hilbert-tér egy jelentős részét, az ún. csúcsos alterét feszítik ki. A Maass-formák Laplace-sajátértékei véges multiplicitásúak: sorba rendezve őket átlagosan
Hilbert-tér egy jelentős részét, az ún. csúcsos alterét feszítik ki. A Maass-formák Laplace-sajátértékei véges multiplicitásúak: sorba rendezve őket átlagosan ![]() távolságra fekszenek egymástól, és a sorozat első
távolságra fekszenek egymástól, és a sorozat első ![]() tagja
tagja ![]() tizedesjegyre kerekítve
tizedesjegyre kerekítve
Selberg azt is megmutatta, hogy a csúcsos altér ortogonális kiegészítőjének minden eleme előáll Eisenstein-sorok folytonos lineáris kombinációjaként: az Eisenstein-sorok ![]() -invariánsak és Laplace-sajátfüggvények, de nem korlátosak.
-invariánsak és Laplace-sajátfüggvények, de nem korlátosak.
A képet finomítják a Hecke-operátorok, amelyek a Laplace-operátor számelméleti megfelelői. Ezek bevezetéséhez rendeljük minden ![]() ponthoz a
ponthoz a ![]() rácsot. Könnyen meggondolható, hogy
rácsot. Könnyen meggondolható, hogy ![]() -ekvivalens pontokhoz tartozó rácsok forgatva nyújtással egymásba vihetők: valójában az
-ekvivalens pontokhoz tartozó rácsok forgatva nyújtással egymásba vihetők: valójában az ![]() pontjai bijekcióban állnak a
pontjai bijekcióban állnak a ![]() -beli rácsokkal forgatva nyújtás erejéig. Tehát egy Maass-formára tekinthetünk úgy is, mint a
-beli rácsokkal forgatva nyújtás erejéig. Tehát egy Maass-formára tekinthetünk úgy is, mint a ![]() -beli rácsok halmazán értelmezett speciális függvényre. Ha most
-beli rácsok halmazán értelmezett speciális függvényre. Ha most ![]() egy pozitív egész, akkor minden
egy pozitív egész, akkor minden ![]() -beli rácsnak van
-beli rácsnak van ![]() darab
darab ![]() indexű részrácsa, amik felett átlagolhatjuk a Maass-formát. Ez az átlagolás az
indexű részrácsa, amik felett átlagolhatjuk a Maass-formát. Ez az átlagolás az ![]() -hez tartozó Hecke-operátor, ami egy konvencionális normálással a felső félsík
-hez tartozó Hecke-operátor, ami egy konvencionális normálással a felső félsík ![]() -invariáns függvényeire a következő alakot ölti:
-invariáns függvényeire a következő alakot ölti:
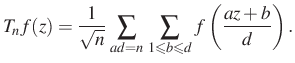
Ehhez a családhoz hozzávesszük még a ![]() kiegészítő Hecke-operátort is, amely az
kiegészítő Hecke-operátort is, amely az ![]() függvényhez az
függvényhez az ![]() függvényt rendeli. A Hecke-operátorok az
függvényt rendeli. A Hecke-operátorok az ![]() önadjungált operátorai, amelyek a hiperbolikus Laplace-operátorral és egymással is felcserélhetők. Ez azt jelenti (egy jól ismert lineáris algebrai tétel szerint), hogy a csúcsos altérnek van olyan Maass-formákból álló bázisa, amelyek az összes Hecke-operátornak sajátfüggvényei. Ha
önadjungált operátorai, amelyek a hiperbolikus Laplace-operátorral és egymással is felcserélhetők. Ez azt jelenti (egy jól ismert lineáris algebrai tétel szerint), hogy a csúcsos altérnek van olyan Maass-formákból álló bázisa, amelyek az összes Hecke-operátornak sajátfüggvényei. Ha ![]() egy ilyen Hecke-Maass-forma, amire
egy ilyen Hecke-Maass-forma, amire ![]() , akkor az
, akkor az ![]() -hez társított másodfokú
-hez társított másodfokú ![]() -függvény az
-függvény az ![]() -nél nagyobb valós részű komplex számokon
-nél nagyobb valós részű komplex számokon
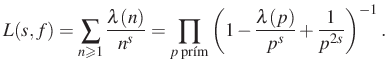
Továbbá, ha ![]() és
és ![]() (a
(a ![]() eset hasonló), akkor a teljes
eset hasonló), akkor a teljes ![]() -függvény
-függvény
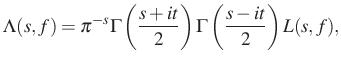
ami kiterjed holomorf egészfüggvénnyé és kielégíti a ![]() függvényegyenletet. Tehát
függvényegyenletet. Tehát ![]() és
és ![]() nagyon hasonlít a Riemann-zetából származtatott
nagyon hasonlít a Riemann-zetából származtatott ![]() és
és ![]() szorzatokra. Valójában
szorzatokra. Valójában ![]() nem más, mint az
nem más, mint az ![]() Laplace-sajátértékű Eisenstein-sorhoz a fenti módon társított
Laplace-sajátértékű Eisenstein-sorhoz a fenti módon társított ![]() -függvény!
-függvény!
Amennyire tudjuk, az ![]() Dirichlet-sorának együtthatói – tehát a Hecke-operátorok sajátértékei az
Dirichlet-sorának együtthatói – tehát a Hecke-operátorok sajátértékei az ![]() Maass-formán – transzcendens számok (ellentétben a korábban felfedezett
Maass-formán – transzcendens számok (ellentétben a korábban felfedezett ![]() -függvényekkel), de a Riemann-sejtés itt is igaznak tűnik: ha
-függvényekkel), de a Riemann-sejtés itt is igaznak tűnik: ha ![]() , akkor
, akkor ![]() valós része
valós része ![]() . Jó okunk van tehát feltételezni, hogy a Riemann-sejtés maga is automorf természetű. Annyit már most bizonyosan tudunk, hogy az automorf
. Jó okunk van tehát feltételezni, hogy a Riemann-sejtés maga is automorf természetű. Annyit már most bizonyosan tudunk, hogy az automorf ![]() -függvényeket együttesen, családokban tudjuk hatékonyan vizsgálni, felhasználva azok közös eredetét.
-függvényeket együttesen, családokban tudjuk hatékonyan vizsgálni, felhasználva azok közös eredetét.
Végezetül nézzünk meg néhány Maass-formát a „valóságban”. Az alábbi ábrákat Fredrik Strömberg készítette, és az ő engedélyével közöljük. Mindegyik ábrán egy Maass-forma abszolút értékének eloszlása látható a ![]() halmazra megszorítva (pontosabban annak az
halmazra megszorítva (pontosabban annak az ![]() feltétellel megadott kompakt részére), ami az
feltétellel megadott kompakt részére), ami az ![]() -re nézve egy fundamentális tartomány. A Maass-formák valós értékűek, mert a
-re nézve egy fundamentális tartomány. A Maass-formák valós értékűek, mert a ![]() operátornak sajátfüggvényei, és ugyanez okozza az ábrák bal-jobb szimmetriáját. Mint egy hőtérképen, a sötétkék szín jelzi a kis értékeket, a vörös pedig a nagyokat.
operátornak sajátfüggvényei, és ugyanez okozza az ábrák bal-jobb szimmetriáját. Mint egy hőtérképen, a sötétkék szín jelzi a kis értékeket, a vörös pedig a nagyokat.
Harcos Gergely
MTA Rényi Alfréd Matematikai Kutatóintézet, Közép-európai Egyetem
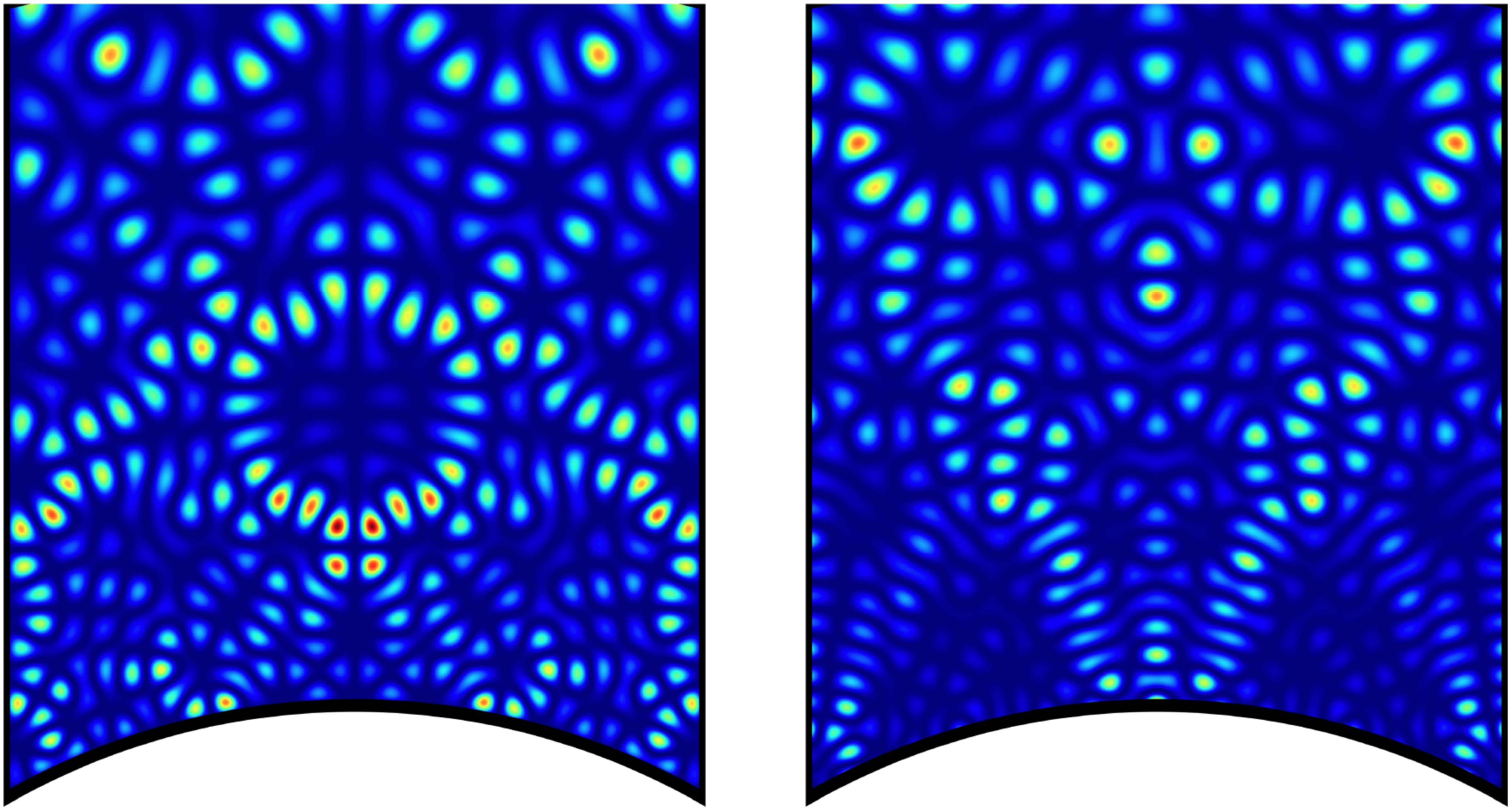
Hecke-Maass-formák ![]() Laplace-sajátértékekkel (Fredrik Strömberg)
Laplace-sajátértékekkel (Fredrik Strömberg)
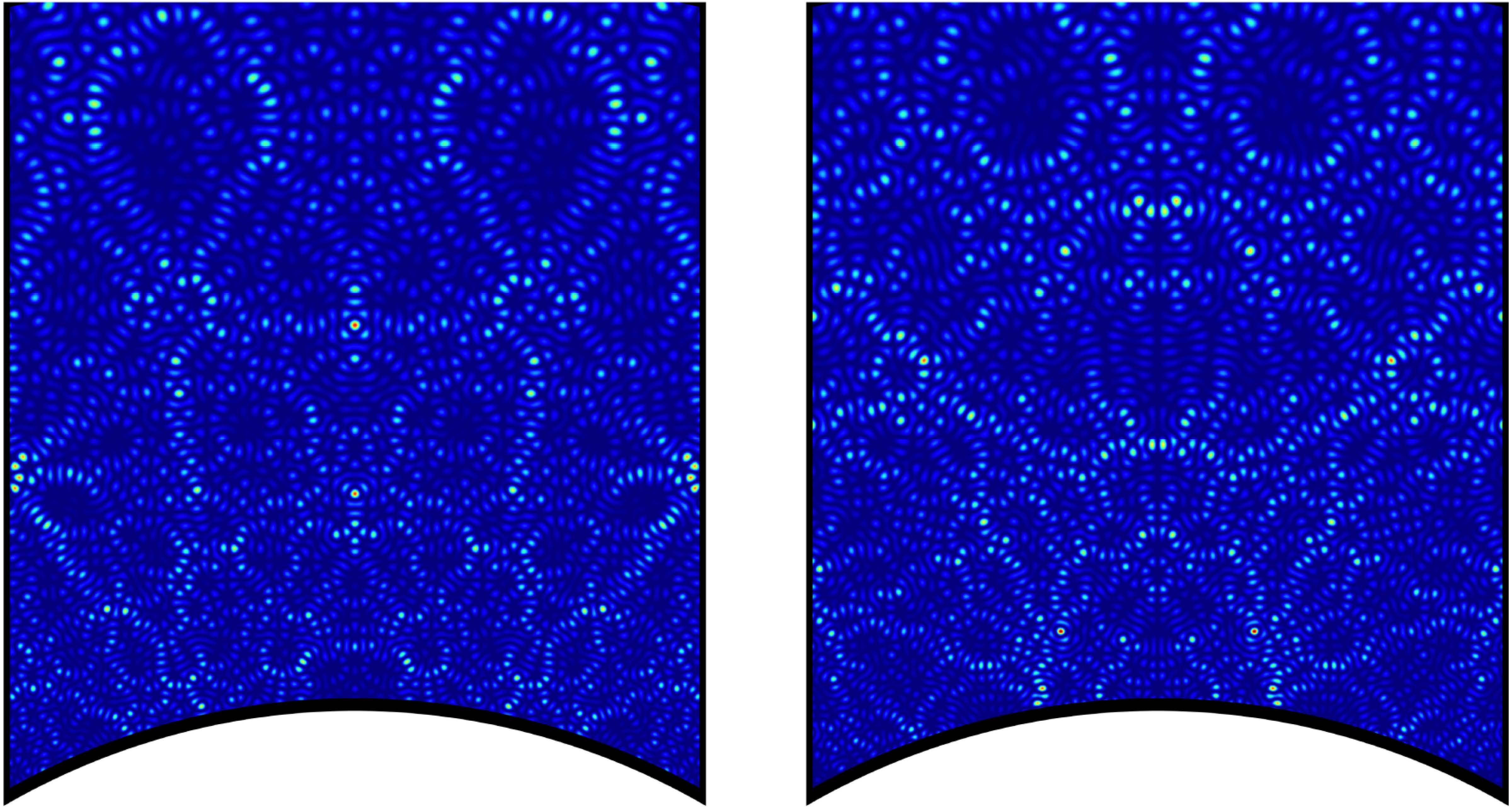
Hecke-Maass-formák ![]() Laplace-sajátértékekkel (Fredrik Strömberg)
Laplace-sajátértékekkel (Fredrik Strömberg)