A cím kissé rejtélyes: a számítógépes algoritmusok a köztudat szerint pontosak és megbízhatók. Az alku során az ügynökök végső érve gyakran az, hogy a kalkulátor is a mondott számot mutatja. Ezzel szemben sajnos fontos feladatok megoldása során is azzal szembesülünk, hogy a kapott eredmény csak közelítő érték, és gyakran kritikus esetben a kapott szám nagyságrendje, vagy az előjele sem helyes. Ennek ellenére van olyan számítógépes módszertan, amely biztosítani tudja a numerikus számítások tetszőleges pontosságát és megbízhatóságát. Ez úgy érhető el, hogy többet kell számolni, és tovább tart a megoldás. Gyakran a gép memóriája is nagy kell hogy legyen.
A pontatlanság egyik oka: Adjunk össze 3 számot, majd igazoljuk, hogy ha ezt lebegőpontos számítógépes rendszerben tesszük, akkor az eredmény lényegében tetszőlegesen távol lehet a helyestől! Matlabban1 például a következőt tapasztalhatjuk. Az
>> A+B+C
utasításra a ![]() értékekkel az eredmény 0, a helyes nyilván 2016. Érdekes, hogy mind az adatok, mind az eredmények lebegőpontos környezetben ábrázolható számok.
értékekkel az eredmény 0, a helyes nyilván 2016. Érdekes, hogy mind az adatok, mind az eredmények lebegőpontos környezetben ábrázolható számok.
Természetesen több megoldás is van erre a problémára. Ilyen a részeredményeknek több lebegőpontos számba való gyűjtése, az ún. error free transformation (EFT), vagy az intervallum-aritmetikán alapuló befoglaló függvények használata.
Legyen ![]() a kompakt valós intervallumok tere. Az intervallum-aritmetika műveletei ezen a halmazon vannak értelmezve. A műveleteket úgy kell definiálni, hogy az
a kompakt valós intervallumok tere. Az intervallum-aritmetika műveletei ezen a halmazon vannak értelmezve. A műveleteket úgy kell definiálni, hogy az ![]() eredménye egy olyan
eredménye egy olyan ![]() intervallum legyen, amely pontosan azon
intervallum legyen, amely pontosan azon ![]() valós számok halmaza, amelyekhez léteznek olyan
valós számok halmaza, amelyekhez léteznek olyan ![]() és
és ![]() valósok, hogy
valósok, hogy ![]() . Itt
. Itt ![]() a négy alapművelet valamelyikét jelöli. Az ilyen aritmetika segítségével követni lehet a kerekítési hibákat, és az adatainkat terhelő bizonytalanság is tükröződhet az eredményekben.
a négy alapművelet valamelyikét jelöli. Az ilyen aritmetika segítségével követni lehet a kerekítési hibákat, és az adatainkat terhelő bizonytalanság is tükröződhet az eredményekben.
Az előző definíció mellett az intervallum-aritmetikát lehet kizárólag a valós aritmetikára támaszkodva is definiálni. Az ![]() és
és ![]() intervallumokra legyen
intervallumokra legyen
Az osztást persze csak akkor értelmezzük, ha ![]() . Érdemes megjegyezni, hogy ez utóbbi feltétel jól megfogalmazott gyakorlati feladatokban a tapasztalataink szerint szinte kivétel nélkül teljesül. A valós műveleteknek ezt a kiterjesztését intervallumokra természetes, vagy naiv intervallum-kiterjesztésnek nevezik. Az utóbbi években vizsgálják az olyan intervallum-aritmetikákat is, amelyek nem csak kompakt intervallumokon definiáltak. Ezeken a nullát tartalmazó intervallummal való osztás is értelmezhető. Például
. Érdemes megjegyezni, hogy ez utóbbi feltétel jól megfogalmazott gyakorlati feladatokban a tapasztalataink szerint szinte kivétel nélkül teljesül. A valós műveleteknek ezt a kiterjesztését intervallumokra természetes, vagy naiv intervallum-kiterjesztésnek nevezik. Az utóbbi években vizsgálják az olyan intervallum-aritmetikákat is, amelyek nem csak kompakt intervallumokon definiáltak. Ezeken a nullát tartalmazó intervallummal való osztás is értelmezhető. Például ![]() .
.
Bár az alapműveletek pontosak a fenti értelemben, mégis, a velük kiszámított bonyolultabb függvények durva becslései is lehetnek a megfelelő értékkészletnek. A gyakran emlegetett példa a következő: az ![]() értékkészlete a
értékkészlete a ![]() intervallumon
intervallumon ![]() . Ezzel szemben az intervallum-kiterjesztéssel adódó intervallum
. Ezzel szemben az intervallum-kiterjesztéssel adódó intervallum ![]() .
.
Az intervallum-aritmetika műveleteinek tulajdonságaival foglalkozik az intervallum-algebra. Számos, a valós műveletekre érvényes tulajdonság változatlanul teljesül az intervallum-műveletekre is (pl. a kommutativitás, asszociativitás az összeadásra és a szorzásra), de általában nincs inverz, és érvényes a szubdisztribúciós tulajdonság: ![]() .
.
Az alapműveletekhez hasonlóan könnyen lehet definiálni az elemi függvények intervallum-kiterjesztését is, tehát a számítógépen kiszámítható függvényeket szinte kivétel nélkül meg lehet valósítani természetes intervallum-kiterjesztésben is.
Az intervallum-aritmetika alkalmazása szempontjából alapvető fogalom a befoglaló függvény. Az ![]() az
az ![]()
![]() -változós valós függvény befoglaló függvénye, ha
-változós valós függvény befoglaló függvénye, ha ![]() érvényes minden
érvényes minden ![]() pontra és
pontra és ![]() intervallumra. Az intervallum-matematika fontos eredménye, hogy az
intervallumra. Az intervallum-matematika fontos eredménye, hogy az ![]() valós függvényből természetes (vagy naiv) intervallum-kiterjesztéssel adódó
valós függvényből természetes (vagy naiv) intervallum-kiterjesztéssel adódó ![]() függvény befoglaló függvény.
függvény befoglaló függvény.
A befoglaló függvényektől természetes azt elvárni, hogy bővebb argumentum-intervallumra ne adjanak szűkebb eredmény-intervallumot. Ezt a feltételt fogalmazza meg az izotonitás: egy ![]() befoglaló függvény akkor izoton, ha
befoglaló függvény akkor izoton, ha ![]() -ból következik
-ból következik ![]() . Az izotonitás szinte minden intervallum-aritmetika implementációra érvényes.
. Az izotonitás szinte minden intervallum-aritmetika implementációra érvényes.
A befoglaló függvények minőségének fontos mutatója a rend: azt mondjuk, hogy az ![]() befoglaló függvény rendje
befoglaló függvény rendje ![]() , ha létezik olyan
, ha létezik olyan ![]() valós konstans, hogy
valós konstans, hogy ![]() teljesül minden
teljesül minden ![]() -re, ahol
-re, ahol ![]() az
az ![]() intervallum szélessége, és
intervallum szélessége, és ![]() az
az ![]() értékkészlete az
értékkészlete az ![]() intervallumon. A természetes intervallum-kiterjesztéssel adódó befoglaló függvények elsőrendűek, de kidolgozott a magasabbrendű befoglaló függvények elmélete is. Az egynél szélesebb intervallumokra a természetes intervallum-kiterjesztést, a kisebbekre pedig a magasabbrendű befoglaló függvényeket szokták ajánlani.
intervallumon. A természetes intervallum-kiterjesztéssel adódó befoglaló függvények elsőrendűek, de kidolgozott a magasabbrendű befoglaló függvények elmélete is. Az egynél szélesebb intervallumokra a természetes intervallum-kiterjesztést, a kisebbekre pedig a magasabbrendű befoglaló függvényeket szokták ajánlani.
A számítógépes megvalósítás során minden intervallum-művelet végrehajtása után a kapott intervallumot módosítani szokás. Az intervallum alsó határát lefelé, felső határát felfelé kell kerekíteni a legközelebbi ábrázolható számra. Ezzel az úgynevezett kifelé kerekítési eljárással el lehet érni, hogy a befoglalási tulajdonság a kerekítési hibák ellenére is fennmaradjon. Ezen a módon számítógéppel automatizálható a garantált megbízhatóságú befoglaló függvények előállítása.
Az intervallum-aritmetikához használatos speciális kerekítéseket az IEEE 754-1985 szabvány biztosítja, ezeket napjaink szinte minden számítógépes processzora támogatja. A hetvenes évek közepétől elérhetők olyan programozási nyelvek, amelyek az INTERVAL adattípus használatát támogatják. Ilyen nyelveken (mint például a C-XSC) még az intervallum-aritmetikát megvalósító szubrutinokat sem kell megírni: a megfelelő befoglaló függvény implementálásához elegendő a függvény kiszámításához használt változók típusát megváltoztatni.
A befoglaló függvényekre támaszkodó numerikus algoritmusok érzékenyek a befoglaló függvény minőségére, pontosságára. A vázolt természetes intervallum-kiterjesztés mellett számos más eljárás is ismert a befoglaló függvények előállítására, például a magasabbrendű deriváltakat is használó ún. középponti alakok, az automatikus deriválásra és monotonitás-vizsgálatra épülő stratégiák a befoglaló függvény javítására, illetve az optimális pontosságú befoglaló függvényt generáló eljárás. Ezek a módosítások természetesen növelik az egy befoglaló függvény kiértékeléséhez szükséges számítások mennyiségét.
Az intervallum-matematikát részletesen tárgyaló jegyzet vagy magyar nyelvű irodalom sajnos még nincs. Angol és német (esetleg orosz) nyelvű bevezető könyveket tudok ajánlani:
- G. Alefeld, J. Herzberger: Einführung in die Intervallrechnung, Bibliographises Institut AG, Mannheim, 1974.
- G. Alefeld, J. Herzberger: Introduction to Interval Computations, Academic Press, New York, 1983.
- H. Ratschek, J. Rokne: Computer Methods for the Range of Functions, Ellis Horwood Ltd., Chichester, 1984.
- S.A. Kalmikov, Yu.I. Sokin, Z.H. Yuldashev: Az intervallum-analízis módszerei (oroszul), Nauka, 1986.
- H. Ratschek, J. Rokne: New Computer Methods for Global Optimization, Ellis Horwood Ltd., Chichester, 1988.
- W. Tucker: Validated Numerics: A Short Introduction to Rigorous Computations, Princeton University Press, 2011.
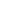
Egy pozitív példa: A SIAM (Ipari és Alkalmazott Matematikai) Társaság 2002-ben 10 numerikus feladatot tűzött ki2. Feladatonként 10 helyes decimális jeggyel 100 dollárt lehetett nyerni. A negyedik megadott feladat a következő függvény minimalizálása volt:
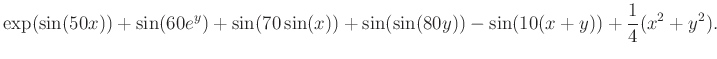
A feladat megoldására egy intervallum-aritmetikára alapuló korlátozás és szétválasztás módszert használtunk. A kapott eredmény a ![]() keresési tartományon a globális minimum értékére a következő alsó- és felső korlátokat adta:
keresési tartományon a globális minimum értékére a következő alsó- és felső korlátokat adta:
Az eredményben a kiemelt első 13 jegy matematikai bizonyítóerővel igazoltan helyes. Ehhez mindössze 0.26 másodperc CPU-idő, minimális memóriaigény (75 részintervallum tárolására volt szükség), 1975 célfüggvény-, 1158 gradiens- és 92 Hesse-mátrix kiértékelés kellett.
Az úgynevezett ,,wrapping effect'' a differenciálegyenletek megoldását nehezíti, még pontos számítás esetén is a kapott eredmény intervallum mérete nagyon nagy lehet:
Az ábrán azt kell megfigyelni, hogy a jobb szélen lévő négyzet körbeforgatásával a befoglaló intervallumok mérete reménytelenül nő. Ennek az oka a rögzített koordinátarendszerben való intervallumos befoglalás.
Mikor nem kell a megbízhatóság?
- Olyan gyakorlati feladatok esetén, amikor költség vagy haszon jellegű a célfüggvény. Ilyenkor a jó közelítő megoldások elegendők.
- Ilyen H.-P. Schwefel példája: A Siemens megbízásából atomerőművek számára kellett a fűtőelemek helyét meghatároznia úgy, hogy javuljon a hatékonyság. Az evolúciós módszerrel talált megoldás több mint 1%-kal volt jobb, mint a korábban ismert. Bár nem tudja, hogy a talált közelítés akár csak helyileg optimális-e, és azt sem, hogy milyen messze van az optimumtól, a megbízó elégedett volt (
 DEM).
DEM).
Mikor kell a megbízhatóság?
- Elméleti állítások igazolására mint például a
- a Kepler-sejtés,
- a Fekete-feladat,
- n-dimenziós gömbhöz illeszkedő azonos méretű gömbök száma (kissing number),
- körpakolási feladatok, vagy:
-
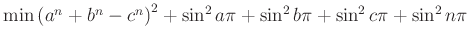 ahol
ahol 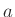 ,
, 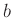 ,
, 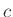 nemnegatív és
nemnegatív és 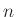 nagyobb mint kettő.
nagyobb mint kettő.
- egyes olyan gyakorlati feladatok esetén, ahol a közelítő megoldás ismerete haszontalan (pl. van-e olcsóbb termelés...),
- kritikus alkalmazásokban, mint a műtéti robotok irányítása.
Csendes Tibor
Szegedi Tudományegyetem
Az érdeklődők számára további anyagok:
A Tudomány Határai, Kossuth Rádió, 2016. VIII. 27., 14:32, interjú Bánhelyi Balázzsal, Csendes Tiborral és Krisztin Tiborral.
http://www.mediaklikk.hu/radio-lejatszo-kossuth/?date=2016-08-27_14:32:00&ch=mr1
Csendes Tibor: Egy intervallum-aritmetikán alapuló algoritmus a szinthalmazok korlátainak megkeresésére. Alkalmazott Matematikai Lapok 17(1993) 19-40,
http://real-j.mtak.hu/456/1/ALKMAT_17.pdf
Csendes Tibor: Közelítő és szimbolikus számítások. Polygon, Szeged, 2007
Csendes Tibor: Számítás garantált pontossággal I., Számábrázolási lehetőségek, Természet Világa 132(2001) 132-134
Csendes Tibor: Számítás garantált pontossággal II., Természet Világa 132(2001) 180-183
Csendes Tibor: Megbízható Számítógépes Eljárások, Szabadegyetemi előadás
https://www.u-szeged.hu/oktatas/megbizhato-szamitogepes/megbizhato-szamitogepes
Pál László és Csendes Tibor: Egy intervallum alapú globális optimalizálási módszer és alkalmazása szenzor lokalizálási feladatra. Alkalmazott Matematikai Lapok 28(2011) 17-39,
http://aml.math.bme.hu/wp-content/uploads/2012/06/28-pal_csendes.pdf
A szerző a Szegedi Tudományegyetem Számítógépes Optimalizálás Tanszéke egyetemi tanára, a fenn megadott cikkek egy része elérhető a http://www.inf.u-szeged.hu/~csendes/publh.html oldalon is.
Korábbi cikkünk a Moore-díjat elnyert Csendes Tiborról és kollegáiról 2016. decemberében jelent meg az Érintőben:
http://ematlap.hu/index.php/tudomany-tortenet-2016-12/391-szegedi-matematikusok-kaptak-a-moore-dijat
Lábjegyzetek
- 1
- A MATLAB olyan matematikai programcsomag, amelyet eredetileg mátrixokkal végzett műveletek elvégzésére és numerikus számításokra dolgoztak ki. Speciális előnyei a jelfeldogozás és a szabályozás területén adódhatnak. Elsősorban mérnökök körében népszerű.
- 2
- Nick Trefethen: A Hundred-Dollar, Hundred-digit Challenge. SIAM News 35(2002)