A filozófia csodálatos hatékonysága a formális tudományokban

A matematikáról alkotott elképezelések közül kettőnek mindenképpen jelentős tábora van. Az egyik a „szolgálólány” szerepét adja a matematikának, és az értékére más tudományokban való alkalmazhatóságában találnak rá. Voltaképpen más formális tudomány, mint például az informatika is osztozik ebben a sorsban, csak ennek az esetében még erőteljesebb a mérnöki tudományokkal való kapcsolat hangsúlyozása. A másik szerint a matematika jelenségei önmagukban is szépek, bármiféle hasznosság, alkalmazhatóság, külső kapcsolat nélkül. A szolgálólány felfogás szerint a matematika művelésének és tanulásának célja és értelme elsősorban a műszaki, társadalom- vagy természettudományos alkalmazhatóságában keresendő. Az esztétikai elképzelés szerint viszont a matematika tiszta és szép, amennyiben – ahogy a mondás tartja – szép az, ami érdek nélkül tetszik. Szinte nincs is középút a praktikusság és a gyönyörködtetés hangsúlyozása között. Érdekes azonban, hogy még az esztétikai felfogást vallók is büszkén emlegetik a műszaki alkalmazásokat, a praktikusság pártján állók pedig még erősebb állítást tesznek és azt is hangsúlyozzák, hogy maguk a matematikai területek létrejötte is külső motivációknak köszönhetők. A szolgálólány kép szolgálatában állók kifejezetten ünneplik az olyan történeti tényeket, mint hogy Faraday erővonalai nélkül nem lenne vektoranalízis, vagy hogy a nagy londoni kolerajárvány és Pearson epidemiológiai érdeklődése nélkül nem lenne maximumlikelihood-módszer, valamint sok más matematikai statisztikai eljárás. Azonban a hasznossági és esztétikai felfogás mellett van egy kevésbé ismert változata a formális tudományok létmagyarázatának, éspedig a nem-empirikus tudományokhoz kapcsolódó motivációk és alkalmazások. Ha vannak is, akik tudják, kevesen vallják be maguknak, hogy a matematika egyes területei, különösképpen az informatikával határos területei jelentős filozófiai motivációk hatására jöttek létre. Ebben az írásban röviden bemutatunk néhány filozófiai motiváltságú témát és biztatjuk az olvasót, hogy legyen nyitott a formális tudományok és a filozófia gyümölcsöző kapcsolatának felfedezésére. Magának ennek az írásnak a címe is erre utal, parafrazeálva Wigner Jenő híres esszéjének, az A matematika csodálatos hatékonysága a természettudományokban címét.[7]

Érvelés, bizonyítás

Hajlamosak vagyunk a matematikára és az informatikára úgy gondolni, mint számoló tudományokra. Ezzel szemben a matematikában bizonyításokon, azaz szöveges érveléseken keresztül vezet az út a tudományos igazság detektálásához. A magas szintű elméleti informatikában pedig nem csak a programozás, hanem a programok helyességének vizsgálata is elengedhetetlen, ami voltaképpen szintén nem más mint bizonyítás. Szabó Árpád klasszika-filológus volt az első, aki rámutatott arra, hogy a levezetés/bizonyítás a matematikában nem fokozatosan jelent meg, a legegyszerűbb érvelésektől a legbonyolultabb indirekt bizonyításokig, hanem robbanásszerűen jött létre, és elsődlegesen indirekt bizonyítások formájában bukkant fel már a legkorábbi érvelő matematikai szövegekben. [13] Szabó szerint a módszer meglepő módon az éleai filozófiából és Parmenidész filozófiai iskolájából eredeztethető. Úgy is fogalmazhatunk, hogy a bizonyítás, mint módszer, teljes fegyverzetben pattant ki az éleai filozófusok agyából. Eredetileg a bizonyítás tehát nem matematikai módszer volt, bár kiváló alkalmazásra talált a matematikán belül.

Szabó Árpád klasszika-filológus 1913–2001 (kép forrása: [6])

A Szabó-féle tézis túloldalán az a kérdés vetődik fel, hogy képesek-e a formális tudományok filozófiai kérdéseket eldönteni, azaz tudnak-e olyan szilárd eszközként működni, ami olyan módon képes nyitott kérdések végére pontot tenni, ahogy a matematikában egy bizonyítás végleg igazolni tud egy sejtést. A válasz nyilván tagadó: a filozófiai kérdéseket filozófiai eszközökkel lehet megválaszolni és sokszor éppen ez az útkeresés a legjobb, ami történhet a filozófiai kutatóival. Mindennek ellenére jócskán találunk olyan alkalmazásokat, amelyekben a filozófiai problémák szabatosan megfogalmazott változata vizsgálat tárgyává tehető és igazságuk kérdése egyértelműen megválaszolgató matematikai precizitással. Két példát mutatunk.

Az egyik Gödel ontologiai istenérve. Ez a Gödel íróasztalának fiókjából előkerült érvelés azt hivatott igazolni, hogy ha bizonyos egészen hihető tulajdonságokkal definiáljuk az isteni lény fogalmát, akkor az érv szerint ilyen lény létezik. Automatizált bizonyításellenőrző módszerekkel kiderítették, hogy Gödel-érve ellentmondást rejt magában. Igaz, azt is sikerült kimutatniuk, hogy ésszerű módosításokkal az érv javítható. Programozási környezetnek az Isabelle/HOL nyelvet választották, ami egy funkcionális, teljes és tiszta típusos programozási nyelv. Persze, minden ilyen érv esetén a kulcskérdés az, hogy a következtetés feltételei fennállnak-e, ha viszont fennállnak, akkor a konklúzió, jelen esetben az isteni lény létezése, az automatikus bizonyításellenőrző matematikusok szerint a módosított értelemben fennáll. [3]

A másik a deflácionizmus problémája. Ennek a fókuszában a következő kérdés áll. Az a mozzanat, amikor állításainkat igaznak minősítjük, vajon minőségileg (esszenciálisan) más-e mint amikor az igazsághoz úgy jutunk el, hogy az adott állítást levezetjük? A kérdés precízebben megfogalmazva a következő: több bizonyítható állításunk lesz, ha alkalmazzuk az igazság egy axiomatikus elméletét, mintha ezt nem tennénk és csak a bizonyításaink végeredményeként kipottyanó álltásokat tekintjük igaznak. A negatív választ Alfred Tarski sejtette meg 1935-ben és Volker Halbach igazolta a 90-es években a számelméletre vonatkozóan egy axiomatikus igazságértelmezést alapul vevő rendszerre. Az aritmetikában a Halbach-féle axiomatikus igazságfogalom tehát olyan, ami nem különbözik szubsztanciálisan a bizonyítással levezetett igazságtól, a jelenléte a nyelvben nem változatja meg a bizonyítható állítások körét. (Stanford Encyclopedia of Philosophy bejegyzés.)

Alfred Tarski (1901–1983), Volker Halbach (1965–)

A nyelvi jelentés használatelmélete

Egy másik téma, amelynek történetében szétválaszthatatlanul kapaszkodnak össze a formális tudományok és a filozófia a logikai operátorok jelentésének problémája. Az egész a tudományos megismerhetetlenség fogalmának XIX. századi előtérbe kerülésével kezdődött. Luitzen Egbertus Jan Brouwer topológiával foglalkozó holland matematikus (akit a barátai Bertus-nak hívtak) állt elő azzal az elképzeléssel, hogy a matematikában is vannak végleg megismerhetetlen állítások, így a kizárt harmadik elve vagyis, hogy minden matematikai állítás vagy tagadása igaz, nem érvényes általánosan. Egyáltalán, éles kritikával tekintett a matematikai igazság fogalmának bármilyen formális leírására. Ahogy írja:

Számomra az „igazság” egy általános érzelmi jelenség, amely „Begleiterscheinung”-ként [kísérőjelenségként] összekapcsolható – vagy nem – a formális matematikával. És éppen ezért nem ismerek fel igaznak, tehát matematikának sem olyan dolgot, ami bizonyos szabályok szerint szimbólumokban fogalmazható meg, és fordítva, el tudok képzelni olyan matematikai igazságot, amely soha nem rögzíthető semmilyen formális rendszerben. [...] De még akkor is, ha a formális rendszer egybeesik az intuitív matematikával, pontosabban mondva, ha a két dolog párhuzamos, akkor is az egzaktság az intuícióban rejlik, soha sem a formulákban. Utazáskor a menetrend pontosságára kell hagyatkoznom, és ez nem azt jelenti, hogy bizonyos, korábban rögzített szabályok szerint egy alapszabályból származtatták azt, hanem, hogy nem tartalmaz nyomdahibát, vagy más szavakkal, hogy teljes mértékben megfelel az összeállítója szándékainak. És ennek a teljes megfelelésnek az érzete alapvetően azonos azzal, amit a matematikai igazság érzékelésének nevezek, ill. amelyet az igazi matematika egyetlen kritériumának tartok. (L. E. J., Brouwer, Collected works. Volume I, 1974, p. 451.)

A nyelvvel szemben tanúsított bizalmatlanság Brouwer számára nem merült ki pusztán egy negatív filozófiai álláspontban. A nyelv és különösképpen a formális nyelv megbízhatatlanságával az emberi elme által pontról-pontra végiggondolt processzusait állította szembe. Brouwer ilyetén kezdeményezésével létre is jött az intuicionista matematikafilozófiai iskola, amely ezzel a verifikacionista gyakorlattal testvérelmélete lett a később orosz konstruktivizmusnak nevezett matematikai/számítástudományi paradigmának.

Az intuicionizmus enyhén szólva nem aratott sikert a matematikusok között. David Hilbert különösen sokat tett azért, hogy gátat vessen az elterjedésének. Váratlan helyről érkezett azonban az intuicionizta táborhoz a segítség: a közönséges nyelv filozófiájának világából. Ludwig Wittgenstein második nagy húzása volt, hogy a nyelvi jelentés használatelméletét bedobta a filozófiai köztudatba (az első a tractatus-i etika volt). Az a nézet, hogy a szavak jelentését kizárólag a kommunikációban betöltött szerepük határozza meg, a felszínen nagyon jól illeszkedik az intuicionisták metafizikai puritanizmusához. Honnan tudhatnánk, hogy mi az objektív igazság, ha még nem láttuk? Ill. honnan tudhatnánk, ha csak úgy szerzünk róla tudomást, hogy bizonyítékokkal állunk elő a létezéséről? A jelentés és igazságtartalom megállapításának embertől független természete kritikája jelenik meg Wittgensteinnél is:

Azt kellene mondanunk, hogy ha követnéd a helyes szabályokat, akkor tudnád, hogy mit jelent a „huhh”? Nem, nyilvánvalóan nem. Milyen értelemben? Nincs tízezer jelentés, ami a „huhh”-é lehet? – Úgy hangzik, mintha az, hogy megtanulod, hogyan kell használni, különbözne attól, hogy ismered a jelentését. De a lényeg az, hogy mindannyian ugyanúgy használjuk. A jelentésének ismerete azt jelenti, hogy UGYANÚGY használjuk, mint a többi ember. A „helyes módon” nem jelent semmit. (Wittgenstein, [12] p. 182)

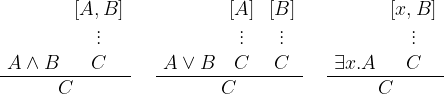
Michael Dummett angol és Dag Prawitz svéd filozófus felkarolta azt a gondolatot, hogy a wittgensteini nyelvhasználatelmélet és a brouweri intuicionizmus a felszínen ugyanazt a viselkedést mutatja. Mindkettőjük számára az elsődleges kísérleti terep a logika és a matematika volt: ezen a „játszótéren” kísérletezhették ki egzakt eszközökkel a használatelmélet tulajdonságait. Ahelyett, hogy a kétes metafizikai státuszú igazságértékekkel definiálták volna a logikai operátorokat, Gerhard Gentzen módszerét követték, ami filozófiai szóhasználattal élve a következő. Két megközelítésben írható le egy logikai szó jelentése. Az első a verifikacionista megközelítés, amely szerint azt kell megmondanunk, hogy mi teszi érvényessé az adott szót tartalmazó mondatot. Ezek a bevezetési szabályok. Például rendre az „és”, „vagy” ill. „létezik” szó esetén:

.

Ezek a szabályok elég világosak, az 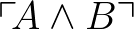fennállásához az 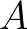és 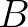együttes fennállása, az 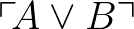fennállásához az 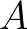és 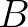közül legalább az egyiknek a fennállása elegendő. Ha szeretnénk érvényesen állítani, hogy létezik olyan 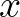, amire 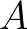fennáll, akkor ehhez elegendő találnunk egy 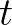-t, amire 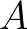fennáll (az 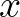változóba helyettesítést nyíllal jelöltük). A másik megközelítés a pragmatikus jelentést helyezi előtérbe. Eszerint a logikai operátorok jelentését az határozza meg, hogy mire jók, azaz ha tudjuk, hogy egy mondat, amiben ők a főszereplők fennáll, akkor mire lehet ebből a tényből következtetni. Az előzőeket folytatva, az úgy nevezett kiküszöbölési szabályok:

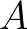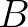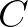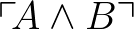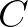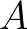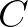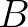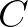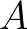Az első az „és” kiküszöbölési szabálya: ha tudjuk, hogy valamint felhasználásával érvényessége ered és érvényes, akkor akkor ebből érvényességére lehet következtetni. A középső az esetszétválasztás következtetési szabálya: ha -ból is következik és -ből is következik és és 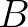közül legalább az egyik érvényes, akkor 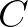is következik, mégpedig az esetszétválasztásban szerepeltetett feltételek nélkül. Az utolsónál feltétel, hogy az 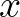változó ne szerepeljen a 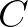mondatban, de lényegében ugyanaz, mint a „vagy” kiküszöbülési szabálya, csak 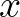-szel paraméterezett végtelen sok esetben. Vegyük észre, hogy a logikai szavak jelentésének ilyetén „definíciója” teljesen a szavak jelentésének használatelméletén alapul. Nem az van ugyanis, hogy megmondjuk, hogy mi egyfajta lexikonszerű fordítása a szavaknak, hanem azt mondjuk meg, hogy milyen esetekben fordulhatnak elő érvényesen és hogyan lehet őket más állítások érvényességének kimutatására felhasználni.

Talán meglepő, de (az induktív típusoknál, lásd később) a bevezetési szabályokból a kiküszöbölési szabályok automatikusan generálhatók. Erre eljárást pl. Thierry Coquand adott, a Coq félautomatikus tételbizonyító program első fejlesztője. Már Gentzen észrevette és Prawitz igazolta azt a sejtést, hogy minden olyan esetben, amikor egy operátor bevezetési szabályát közvetlenül a kiküszöbölési szabálya követi, akkor már korábban olyan helyzetben voltunk, hogy a konklúzió levezethető volt. Ezt a Gentzen által észrevett elvet Dummett harmóniának, Prawitz inverziós elvnek nevezte, Thierry Coquand pedig egyszerűen algoritmikusan beépítette abba a formális vagy programozási nyelvbe, amit az induktív konstrukciók kalkulusának (CIC) nevezett. Merthogy a kiküszöbölési szabályokat indukciós szabályoknak is nevezik. Hogy miért, azt mindjárt megértjük.

Finitizmus

David Hilbert a XX. század hajnalán még képes volt egyben látni a matematikát. És hatása is volt arra, hogy formálja a matematikai problémafelvetéseket. Nevéhez fűződik az, hogy a lehető legtágabban értelmezett módon lehessen a matematikát művelni és ne korlátozza senki a matematikus problémamegoldó repertoárját. Hilbert foglalkozott a bizonyítási módszerek bővítésével is: első jelentős munkájában az úgy nevezett Gordan-problémát ilyen módszerrel oldotta meg. Egy olyan segédtételt használt, az úgy nevezett bázistételt, amiben a szükséges véges generátorrendszer létezését egyfajta indirekt rekurzív egzisztenciabizonyítással igazolta. A bizonyításában felhasznált módszerek 1890-ben legalább is olyanok voltak, amiket később vizsgálat tárgyává kellett tenni. Ez egyáltalán nem meglepő, hiszen akkoriban még nem létezett a halmazelmélet és a tételben a függő kiválasztásra való hivatkozás olyan húzás volt, aminek a matematikai megalapozottságát csak Hilbert későbbi szerzőtársa, Bernays tisztázta 1942-ben. A nem igazolt anekdota szerint, amikor Gordan olvasta Hilbert bizonyítását, úgy fogalmazott, hogy „ez nem matematika, hanem teológia”; később viszont a legendárium szerint, hogy „meggyőztem magam arról, hogy még a teológiának is megvannak az érdemei”.

David Hilbert tehát különös figyelmet fordított arra, hogy legyen olyan eszköz a kezében, amely nem hitbeli, ideológiai alapon, hanem matematikai percizitással képes eldönteni, hogy egy bizonyítási módszer érvényes-e a matematikában vagy sem. A bizonyításokat matematikai vizsgálat tárgyává tette, de ezzel együtt figyelnie kellett arra, hogy maguk a vizsgálatok már olyanok legyenek, amelyek evidensek, így érvényességükhöz nem fér kétség. Ezt a legszűkebb, tartalmas és evidens matematikát nem definiálta pontosan – nem véletlenül –, és finit matematikának nevezte. Amiként a brouweri intuicionizmus nem definiálható (erre von Neumann is felhívja a figyelmet Gödellel való levelezésében), úgy a finitizmus is a legelemibb matematikai szemléletre hivatkozva határolható csak körül. Például a 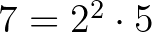egészen biztosan finit állítás (legfeljebb hamis). A „minden 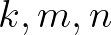természetes számra a 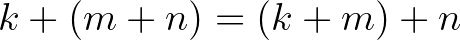” már alulról súrolja a finitizmus határát, a nevezetes Péter–Ackermann-függvény definíciója, ami rekurzív, de nem primitív rekurzív, pedig talán már éppen a finitizmus határán billeg. Tézis, amely mellett W. Tait érvelt, hogy a finit matematika a primitív rekurzív aritmetika.[11] Valójában ez a tézis csak iránymutató, a finitista érvelések nem csak az aritmetikai fogalmakra alkalmazhatók, hanem olyan típusú objektumokra is, amelyek hasonlóak az aritmetikai tárgyakhoz, amelyekre vonatkozó érvelési és függvénydefiníciós szabályok hasonlóak hozzájuk. A természetes számok típusának finit konstrukciói nagyon hasonlítanak a természetes levezetéshez:

.

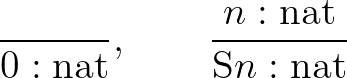Kiküszöbölési szabálya pedig a jól ismert teljes indukció érvelési sémája:

,

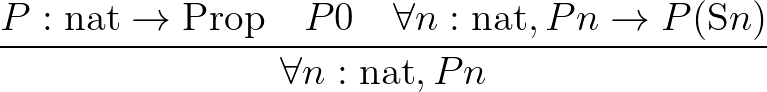ahol 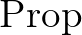az állítások típusa. Nagyon lényeges, hogy a finitizmus filozófiai szempontból redukcionista irányzat, hiszen kitünteti tárgyaknak egy reduktív osztályát, amelyet ontológiailag elsődlegesnek tekint. Amikor tehát azt állítjuk, hogy a 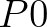állítás teljesül, akkor ezt a klasszikushoz képest másként, úgy kell értenünk, hogy bizonyítható és létezik olyan finit konstrukció, amely mutatja, hogy 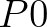érvényes. Ezért a teljes indukció sémáját inkább a következő módon kéne írnunk:

,

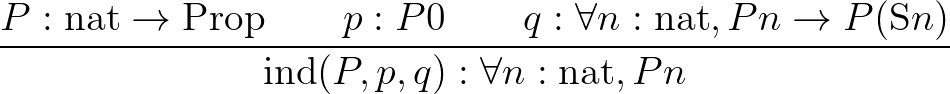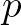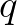vagyis ha léteznek és bizonyítások mint fent, akkor megköveteljük, hogy létezzen egy 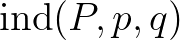konstrukció is, amely 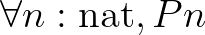bizonyításának felel meg. Ebből a felfogásból nem nehéz eljutni oda, hogy felismerjük, a teljes indukció analógiájára létezniük kell finit primitív rekurzív megadású függvényeknek is:

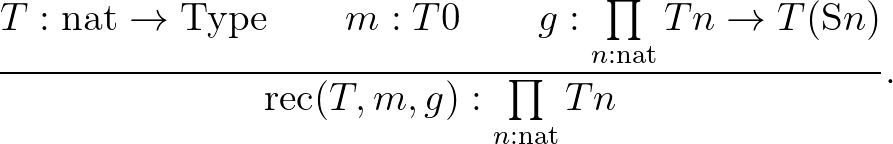
Itt 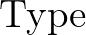típusok típusa, pl. maga 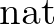egy típus: 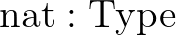. 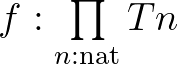pedig azt jelenti, hogy 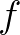olyan finit konstrukció, hogy 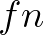tetszőlges 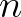esetén egy 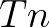típusú finit konstrukció. Ha például 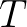a konstans 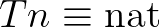, akkor a fenti rekurziós szabály éppen a -ba képező primitív rekurzióval definiálható sorozatokat adja meg:

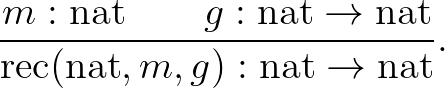
Az érdekes, és ezt már korábban is láttuk, hogy nagyon hasonló induktív módon definiálható az aritmetikán kívül is sok más finit típus. Az induktívan definiált konstruktív típusokról szól Coquand szerzőtársának, Christine Paulin-Mohringnak a rendkívül intuitív leírása.

Szemléletesen, egy induktívan definiált típus konstruktorok egy teljes listája által adott. A rájuk vonatkozó indukciós elvvel érvelünk a típus elemeivel kapcsolatban és a konstruktorokon függvényeket adunk meg, amik alkamasak az adott típus felett értelmezett primitív rekurzív függvények definiálására. (Christine Paulin-Mohring, 1990)

Meglepő, de igaz, hogy induktív típus az egyenlőség is,

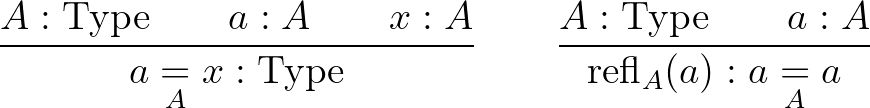
az indukciós szabálya pedig:

.

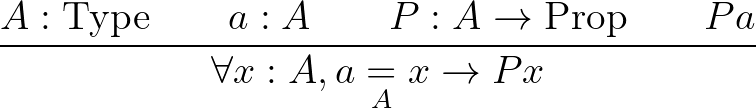Egészen világos mit mond ez a szabály: ha valami 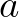-val egyenlő, akkor ugyanazok a tulajdonságai, mint 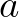-nak. Tehát ez az azonosságra vonatkozó ismert Leibniz-szabály. Ami viszont a redukcionista rendszerekben felvetődik, hogy vajon ez az egyenlőség eldönthető-e. A másik hasonló redukcionista rendszerben, az intuicionistában például nem feltétlenül igaz, ho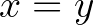gy vagy 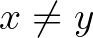. Ha a fenti egyenlőséget csak a természetes számok típusára korlátozzuk, akkor viszont érdekes módon az így definiált egyenlőség eldönthető lesz annak ellenére, hogy a finitizmus sem tud feltétlenül bizonyítást adni tetszőleges 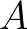esetén 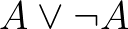-ra, hiszen egyáltalán nem biztos, hogy ha 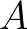bizonyítása finiten nem konstruálható, akkor 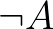-é viszont igen. (Ne felejtsük el, hogy egy finitista szerint 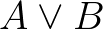bizonyításának is szelektívnek kell lennie, azaz csak akkor tudjuk, hogy 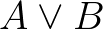igaz, ha már egy véges eljárás legyártotta, hogy a diszjunkció melyik tagját tudjuk levezetni, majd a levezetést is megadjuk.) A természetes számok típusának egyenlősége megragadható a primitív rekurzió elve felől is. A 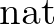-beli induktív egyenlőség eldönthetősége éppen azon alapszik, hogy definiálható rekurzívan, a természetes számok generálásának mintája alapján. Két szám egyenlő, ha mindketten nullák vagy ha mindegyik valaminek a rákövetkezője és amiknek ők a rákövetkezői, azok egyenlők, más esetben pedig nem, azaz a nulla nem egyenlő semminek a rákövetkezőjével. Egy olyan rendszerben, amikor a metaelméletben (a programozási nyelvben magában is) megvan a primitív rekurzív definíció lehetősége, akkor a Leibniz-féle általános induktív és az algoritmikusan definiált egyenlőség, legalább is a nat-ra vonatkozóan, ugyanaz. Ebből viszont könnyen következik, hogy a nat feletti egyenlőség eldönthető is, mert az egyenlőséget definiáló primitív rekurzív algoritmus az eldönthetőséget garantálja. Érdekes filozófiai kérdésre kaptunk tehát betonbiztos matematikai választ: a természetes számok felett algoritmikusan definiált egyenlőség más-e, mint a természetes számok felett induktív típusként definiált Leibniz-féle egyenlőség? A válasz: nem, ez a két fogalom extenzionálisan egybeesik. Vegyük észre, hogy a halmazelmélet esetén ez nincs így. A szokásos felépítésben a halmazok egyenlősége definiálható a középiskolában tanult módon: egyenlők, ha elemeik megegyeznek, de azt, hogy ez a logikai egyenlőséggel egybeesik, azt axiómában (a meghatározottsági axiómában) kell rögzítenünk. Ezzel szemben a fenti konstruktív rendszerben a két nat-egyenlőség levezethetően azonos.

Strukturalizmus

A 20. század első felében a matematikai logika kutatási irányai a megalapozási problémák körül koncentrálódtak. A kezdeti feladat, hogy biztos alapokra kell helyezni a matematikát, ezzel elkerülendő a homályos megfogalmazásokból adódó félreértéseket, hamar filozófiai problémákba torkollt. Osztályok, halmazok vagy típusok-e a matematika építőkövei? Vagy inkább természetes számok, finit vagy intuicionista konstrukciók? A szigorúság és egzaktság iránti vágy kevés volt a sikerhez és több lépésben nem várt komplikációkhoz vezetett. Először azzal kapcsolatban, hogy igaz-e a kizárt harmadik törvénye az osztályokra, másodszor pedig, hogy egyáltalán igazolható-e a matematika ellentmondásmentessége. A zavarba ejtő negatív válaszok farvizén olyan új koncepciók úsztak be a matematikába, mint a halmazelmélet és a transzfinit indukció, a másik túloldalon, a véges matematika felől pedig a véges algoritmus, és a rekurzív függvények bonyolultságelmélete. A matematikát érintő filozófiai kérdések tisztázása természetszerűleg kikerült a matematika érdeklődési köréből, hiszen a matematika az, amivel a matematikusok foglalkoznak, a filozófia pedig az, amivel a filozófusok. A megalapozási problémák helyett a matematika alapjai nevű tudományterület visszahúzódott a halmazelmélet vagy típuselmélet belső kérdései közé.

A következő motivációs löket, ami a filozófia felől érkezett, egy olyan felvetés volt, ami elutasította a megalapozási paradigmák egy nagyon lényeges kulcskérdését, éspedig, hogy pontosan mik is a matematika alapvető építőkövei. Paul Benacerraf az 1965-bel útjára indított azonosítási problémáján keresztül azzal állította kihívás elé a matematikafilozófusokat, hogy rámutatott, nem lehet úgy egy külső keretrendszerben értelmezni az individuum jellegű matematikai entitásokat, hogy azoknak ne legyenek olyan patologikus tulajdonságai, amelyek a definiálandó entitásnak szándékolt jelentésében nincsenek benne. Paul Benacerraf a természetes számok halmazelméleti definícióját tűzte képzeletbeli céltáblájára. Ismeretes az egyedi természetes számok legalább kétféle nevezetes halmazelméleti definíciója, egyfelől a véges von Neumann-rendszámok:   

von Neumann: 

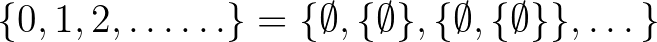
és a Zermelo-rendszámok: 

   Zermelo: 

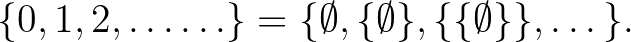
Bár mindkettő megragadja a természetes számok legjellegzetesebb tulajdonságait, mégis vannak ráadásul különböző olyan sajátosságaik, amelyek alapját szolgáltatják annak a kritikának, hogy sikerült-e valóban a természetes számokat és csakis azokat definiálni. Az első esetben igazak például az 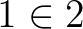és 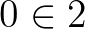állítások, míg a második esetben 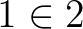teljesül, de 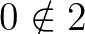. Akik tehát más halmazelméleti definíció szerint tanulták a természetes számokat, nem fognak tudni megegyezni abban, hogy mi egy természetes szám, mindig elő fognak jönni olyan állítások, amiket az egyik igaznak, a másik hamisnak fog érzékelni. Benacerraf csatlakozik Wittgenstein azon, a Traktátusban megjelenő, állításához, hogy a tárgyak csak az egymással való relációjukban értelmezhetők. Ez a tézis adta meg a kezdő lökést a strukturalizmus nevű matematikafilozófiai irányzatnak, amelyik szerint a matematika építőkövei nem abszrakt tárgyak, hanem a matematikai struktúrák. 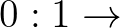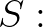Például a természetes számok N objektumát nem az elemei definiálják, hanem az egyelemű objektum és két művelet:  N és   N 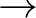 N, valamint ezek tulajdonságai. Ez a felfogás rendkívül szoros kapcsolatban áll a kategóriaelmélettel, amelyben két típusú alapfogalom van, az objektum és a köztük lévő morfizmusok. 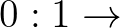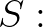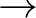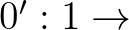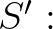Ezek szerint az N objektumot a hozzá tartozó  N és   N  N morfizmusokkal természetes szám objektumnak nevezzük, ha bármely M objektumra és  M és   M 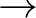 M pontosan egy olya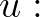n   N 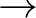 M morfizmus létezik, hogy az alábbi diagram kommutál:

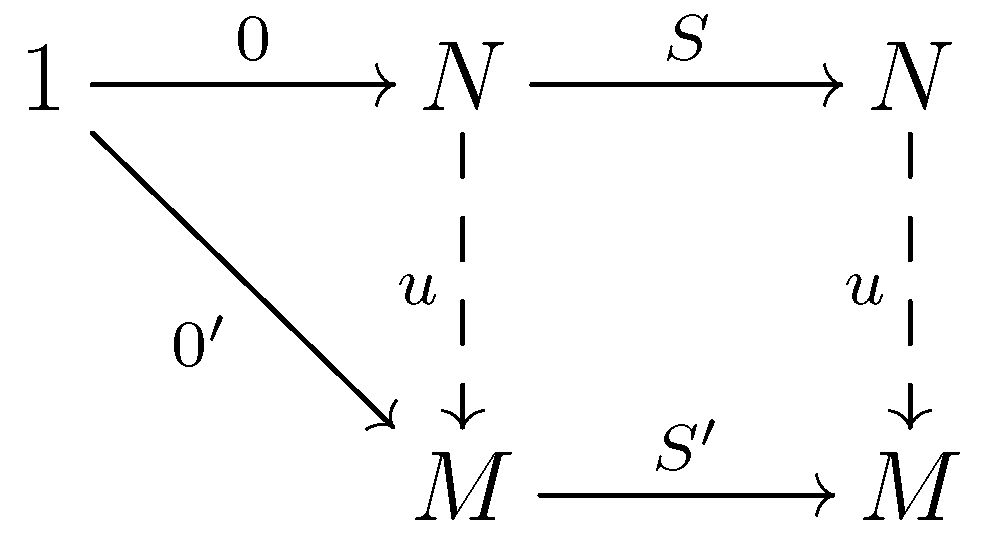
A morfizmusok komponálhatók, a kommutáció azt jelenti, hogy bármely két párhuzamos morfizmus egyenlő. Például , ami azt fejezi ki, hogy a 0 természetes számot a -re cseréli az morfizmus. Ez a diagram persze értelmezhető a halmazok kategóriájában, ahol az objektumok halmazok, a morfizmusok az adott halmazok közötti függvények, a morfizmusok kompozíciója függvénykompozíció. Ekkor a diagram kifejezi, hogy milyen tulajdonságokkal kell rendelkezni a természetes számok 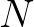halmazának. Ezeknek a tulajdonságoknak megfelelnek von Neumann és Zermelo természetes számai is. Ám, ezek csak egyedi természetesszám-struktúrák lesznek a halmazok kategóriáján belül és nem maguk a természetes számok. Az egyedi természetes számoknak külön-külön nincs értelmük, csak egymáshoz képest tudnak létezni. Éppen ezért minden további nélkül kidobhatjuk akár a von Neumann, akár a Zermelo-féle megnyilvánulási formáikat, ha azt akarjuk, hogy ne legyenek meg a Benacerraf által említett patologikus tulajdonságaik. Ha megadunk egy konstrukciót vagy bebizonyítunk valamit a Zermelo-féle természetes számokról, az teljesülni fog-e Neumann számaira? Ha a kategóriaelméleti absztrakcióval megadott számokkal dolgozunk, akkor mindkettőre teljesülni fog. A diagram azonban nemcsak a halmazok kategóriájában értelmezhető, hanem tetszőleges kategóriában, erre adunk két példát.

• A pontozott halmazok kategóriájában az objektumok halmazok, melyeknek van egy kijelölt eleme, a morfizmusok pedig függvények, amelyek a kijelölt elemet a kijelölt elemre képezik. Ebben a kategóriában a természetes szám objektum a természetes számok a végtelennel kiegészítve.
• A számítógépes programok kategóriájában az objektumok típusok, a morfizmusok pedig olyan programok (algoritmusok, kiszámítható függvények), amelyek bemenetükön adott típusú adatot várnak, és amelyek kimenete szintén a megfelelő típusú. Itt a természetes szám objektum annak felel meg, hogy az adott nyelvben van egy természetes szám típus.

A kategóriaelmélet azon alapgondolata, hogy az objektumok „elemei” nem vizsgálandóak, hanem azok minden tulajdonságát csak a morfizmusok adják meg, nagyon jól harmonizál a benacerrafi strukturalizmus azon ideájával, hogy a tárgyak a relációk nélkül nem léteznek. Így nem csak „nem szabad belenézni az objektumokba”, de nem is lehet és nem is kell.

Ezt az alapgondolatot a számítógépes bizonyítás-ellenőrzésben gyakran használjuk: amikor egy matematikai bizonyítást kódolunk számítógépen, érdemes a legabsztraktabb, kategorikus megfogalmazást használni, mert formálisan az a legegyszerűbb – lévén nem függ az implementációs sajátosságaitól. Ez azt is eredményezi, hogy könnyen újrafelhasználható lesz a bizonyításunk más kontextusokban. A programozásban ezt kód-újrahasznosításnak nevezik. A gyakorlatban használt számítógépes bizonyítás-ellenőrző rendszerek Per Martin-Löf típuselméletének valamelyik változatára épülnek. A típuselméletben a természetes számok a fenti kategorikus módon vannak megadva (a típusok felelnek meg a kategóriaelméleti objektumoknak, a típusok elemei (termek) pedig a morfizmusoknak). Fel lehet-e építeni a matematikát a halmazelmélet helyett a típuselméletet vagy a kategórialméletet használva? A tapasztalat azt mutatja, hogy igen. A Lean bizonyítórendszerben formalizálták az egyetemi matematika tananyag nagy részét [8] és a perfektoid tereket [2], amelyekért 2018-ban Peter Scholze Fields-érmét kapott. A Coq rendszerben bizonyították a négyszíntételt [4] és a Feith–Thompson-tételt [5]. Ezek a formalizálások nem használják a halmaz fogalmát, és nem is kell választaniuk von Neumann vagy Zermelo között, amikor a természetes számokat használják.

A típuselméletben a 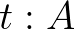-nak (ejtsd: 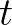-nek típusa 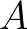vagy 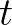lakója 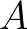-nak) hasonló a szerepe, mint a 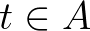-nak a halmazelméletben, de van egy alapvető különbség. A 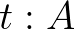nem egy logikai állítás, azaz nem lehet állítani, hanem a nyelv más státuszú dormája, egy ítélete. Míg a halmazelmélet az elsőrendű logikára épül, a típuselmélet tartalmazza a logikát magát. Az elsőrendű logikában az ítéletek „ 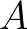egy állítás”, illetve „ 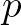bizonyítja 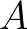-t” alakúak, például a halmazelméletben a „ 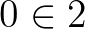egy állítás” ítélet levezethető, és ha von Neumannt követjük, akkor van olyan 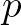, amelyre a „ 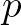bizonyítja 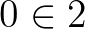-t” állítás levezethető. A típuselméletben a „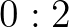” sem nem állítás, sem nem ítélet, mert a „” bal oldalán termnek, jobb oldalán pedig típusnak kell állnia ahhoz hogy az ítélet jól formált legyen, de 0 és 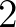mindketten termek. Ez analóg azzal, hogy az elsőrendű logikában a „ 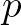bizonyítja 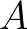-t” csak akkor jól formált, ha 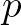egy bizonyítás, 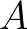pedig állítás. Vegyük észre, hogy maga Bertrand Russell is ezzel a megoldással kívánta kiköszöbölni a Russell-paradoxont a Principia Mathematica rendszeréből: nála is az 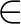jel bal és jobb oldalán nem állhat bármi, csak aminek a típusa ezt lehetővé teszi.

A típuselméletben a természetes számok típust alkotnak, a logikai állítások is típusok, ám a természetes számok típusa nem logikai állítás. Jól ismert, hogy a logikai állításokat típusokkal reprezentálhatjuk (Curry–Howard-megfeleltetés). Viszonylag új fejlemény a Fields-érmes Vladimir Voevodsky állításkarakterizálása. Eszerint azok a típusok állítások, amelyek bármely két lakójára van az egyenlőség típusnak egy eleme. Tehát 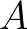állítás, ha tetszőleges két 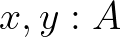-ra létezik 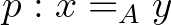. Voevodsky megadta azt is, hogy mely típusokat nevezhetjük halmaznak: 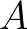halmaz, ha tetszőleges 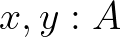-ra és 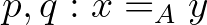-ra létezik 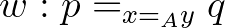. Utóbbiban az egyenlőség iterált változatát használtuk: ha 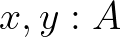, akkor 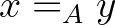típus, és ha 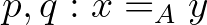, akkor természetesen 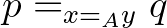is egy típus. Újrafogalmazva: egy típus halmaz, ha bármely két elemének egyenlőség-típusa állítás. Az egyenlőség típus segítségével a típusoknak megadható egy hierarchiája: állítások, halmazok, groupoidok, 2-groupoidok, és így tovább. Az intuíció ezekre az elnevezésekre a homotópia-elméletből származik: a típuselmélet számára Voevodsky megadta a homotopikus modelljét, amelyben a típusok absztrakt topologikus terek (szimpliciális halmazok), a típusok elemei a terek pontjai, az egyenlőség típus pedig a térben egy útnak felel meg.

2012-ben a Princeton Institute for Advanced Studies-ban egy éven át együtt dolgoztak számítógéptudósok, matematikusok és filozófusok a típuselmélet homotopikus modelljén, és közösen írtak egy könyvet homotópia-típuselmélet címmel [10], amely matematikusoknak szóló bevezető a típuselméletről. A könyvben Peter Aczel magyar származású angol matematikus javaslatára kidolgozták annak a gyakorlatát, hogyan kell a matematikai érvelést típuselméletben, de informálisan végezni. A típusok homotópia-hierarchiáján túl a könyv egy további újdonsága a magasabb induktív típusok: ezek olyan típusok, amelyek a természetes számok típusához hasonlóan konstruktorokkal vannak megadva, de egyenlőség-konstruktorokat is tartalmazhatnak, amelyek a kvócienseket általánosítják. Ez lehetővé tette például a valós számok konstruktív és absztrakt megadását Cauchy-sorozatokkal. (Ugyan Bishop-tól [1] régen ismerjük a valós számok konstruktív megadását, de az reprezentációkkal dolgozik, nem absztrakt módon.)

A homotópia-típuselmélet fő újdonsága azonban Voevodsky univalencia axiómája. Ennek egyik következménye, hogy bijekcióban levő halmazok egyenlőek. Tehát ha egy matematikai állítást bebizonyítunk egy halmaz összes eleméről, az minden más, vele bijekcióban álló halmazra is igaz lesz. 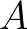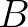Fontos, hogy itt figyelembe vegyük, hogy csak a halmazok elemeinek egyenlőség-típusa állítás, a halmazoknak maguknak az egyenlősége már nem állítás, hanem halmaz: ha és halmazok, akkor 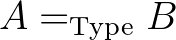szintén halmaz, hiszen több különböző bijekciónk is lehet két halmaz között. Például a 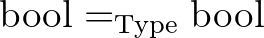egy kételemű halmaz, mert két különböző bijekció van 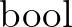-ból önmagába.

A univalencia azért kompatibilis a típuselmélettel, mert a típuselmélet a kategóriaelmélethez hasonlóan reprezentáció-független objektumokkal dolgozik, és a nyelvben nem lehet olyan állításokat kifejezni, amelyek például megkülönböztetik von Neumann és Zermelo természetes számait. Az első ilyen nyelvet a Kanadában élő magyar matematikus, Makkai Mihály adta meg a 90-es évek elején [9]. A nyelv neve függő típusos elsőrendű logika, szintén Martin-Löf típuselméletére épül, és Voevodsky közvetlen inspirációi között volt.

A homotópia-típuselmélet egy számítógépes implementációja a Cubical Agda programozási nyelv, amelyben a univalencia már nem axióma, hanem bizonyítható állítás. Ez már nem szimpliciális halmazokra (magasabbdimenziós háromszögekre), hanem kubikális halmazokra (magasabbdimenziós négyzetekre) épül. Nyitott kérdés, hogy szimpliciális halmazokkal megadható-e a homotópia-típuselmélet konstruktív modellje (Voevodsky modellje klasszikus volt, ezért programozásra nem használható).

Mindezt azért szerettük volna elmondani, hogy érzékeltessük: a matematikafilozófia nem pusztán szépelgés és morfondírozás azzal kapcsolatban, hogy milyen természetű dolog a matematika. A filozófiának közvetlen motiváló hatása van a matematikára és az informatikára. Olyan nem járt utakat nyit meg, amiket az alkalmazások szívesen fogadnak és amik hatékonyabbá teszik a régi úton már nehézkesen döcögő gyakorlatokat. Tény, hogy a matematikustársadalom számára a halmazokétól nagyon eltérő tulajdonságokkal rendelkező típusok idegen világnak minősülnek. De éppen ezt tanulhatjuk meg a filozófusoktól: ha nyitottak vagyunk teljesen új gondolatmenetek mentén haladni, akkor meglepően új matematikai, akár hatékony informatikai alkalmazásokra is rábukkanhatunk.

Irodalomjegyzék

[1] E. Bishop and D. Bridges. Constructive Analysis. Grundlehren der mathematischen Wissenschaften. Springer Berlin Heidelberg, 2012.

[2] Davide Castelvecchi. Mathematicians welcome computer-assisted proof in ‘grand unification’ theory. Nature, 595(7865):18-19, July 2021.

[3] David Fuenmayor and Christoph Benzmüller. Types, tableaus and gödel’s god in isabelle/HOL. Archive of Formal Proofs, 2017. https://isa-afp.org/entries/Types_Tableaus_and_Goedels_God.html, Formal proof development.

[4] Georges Gonthier. The four colour theorem: Engineering of a formal proof. In Deepak Kapur, editor, Computer Mathematics, 8th Asian Symposium, ASCM 2007, Singapore, December 15-17, 2007. Revised and Invited Papers, volume 5081 of Lecture Notes in Computer Science, page 333. Springer, 2007.

[5] Georges Gonthier. Engineering mathematics: the odd order theorem proof. In Roberto Giacobazzi and Radhia Cousot, editors, The 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL '13, Rome, Italy - January 23 - 25, 2013, pages 1-2. ACM, 2013.

[6] Gazda István and Bodorné Siposné Ágnes, editors. Emlékkötet Szabó Árpád születésének 100. évfordulójára. Magyar Tudománytörténeti Intézet, 2013.

[7] Wigner Jenő. The unreasonable effectiveness of mathematics in the natural sciences. Communications on Pure and Applied Mathematics, 13:1-24, 1960.

[8] The mathlib Community. The Lean mathematical library. In Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2020, pages 367-381, New York, NY, USA, 2020. Association for Computing Machinery.

[9] Makkai Mihály. Az absztrakt halmazok elmélete függő típusos elsőrendű logikára alapozva. Magyar Filozófiai Szemle, 58:69-92, 2014.

[10] The Univalent Foundations Program. Homotopy type theory: Univalent foundations of mathematics. Technical report, Institute for Advanced Study, 2013.

[11] William W. Tait. Finitizmus. In Csaba Ferenc, editor, A matematika filozófiája a 21. század küszöbén. Osris, 2003.

[12] Ludwig Wittgenstein. Wittgenstein's Lectures on the Foundations of Mathematics, Cambridge, 1939. University of Chicago Press, 1989.

[13] Szabó Árpád. A görög matematika. Magyar Tudománytörténeti Intézet, 1997.