Hogyan tanul a neurális háló?

Bevezetés

Amint arról a decemberi Érintő is beszámolt, 2024-ben az amerikai John J. Hopfieldnek és a kanadai Geoffrey E. Hintonnak ítélték oda a fizikai Nobel-díjat a gépi tanulás és mesterséges neurális hálózatok területén – közkeletű kifejezéssel: a mesterséges intelligenciában – elért elévülhetetlen érdemeikért. Simon L. Péter akkor megjelent cikke már nyújtott némi betekintést a neurális hálók alapjaiba. A mostani, Maga Balázzsal közös írásukban már a neurális hálók játsszák a főszerepet.

Noha a neurális hálók tanításának mélyebb megértése hosszú, és esetleg fáradságos matematikai előkészületeket igényel, mindannyian szeretnénk legalább intuitív képet kapni arról, hogy nagyjából mi is történik egy neurális háló tanítása és működése során. A jelen cikk ezt a célt igyekszik megvalósítani.

Mi is egy neurális háló?

2025-ben már számtalan dologra használunk mesterséges intelligencián (AI) alapuló eszközöket. Az AI képeket vagy egyéb, szenzorokkal érzékelhető jeleket, adatsorokat osztályoz – ezek bonyolult összehangolása révén például autót vezet –, emberi vagy programozási nyelvek között fordít, CT-felvételeken rákos elváltozásokat azonosít, vagy éppen sakkozik. A viszonylag frissen nagy népszerűséget kivívott alkalmazások szöveget, képet, vagy akár zenét generálnak, ezek révén pedig a technikai dolgokkal kevésbé foglalkozó emberek számára is testközelbe kerül. Ezen eszközök mélyén neurális hálók találhatók, amelyek bizonyos szempontból igen egyszerű gépek: kapnak egy bemenetet, azzal valamit manipulálnak, majd legyártanak egy kimenetet. Azaz egy neurális háló valójában nem más, mint egy függvény, ráadásul sok szempontból egyszerűbb, mint amilyenekkel akár a középiskolai órákon találkozhatunk.

Persze ez a bemenet-kimenet pár olyasmi, amit egy számítógép kezel, így mindkettő számokból kell álljon. Nagyon sok típusú adat eleve olyan, hogy számokból áll, még ha ez nem is látszik róla közvetlenül. Példának okáért egy digitális képet eszközeink egy hatalmas számtömbként tárolnak: egy RGB (piros-zöld-kék) színkódolású, 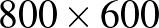$800\times 600$ pixeles digitális kép valójában egy 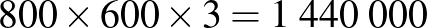$800\times 600\times 3=1\;440\;000$ számból álló számtömb, amelynek minden egyes pixelét három darab, 0 és 255 közötti egész írja le, rendre megadva a vörös, a zöld és a kék szín intenzitását az adott képponton. Így az az ember számára (általában) nyilvánvaló példafeladat, ahol egy kutyát vagy egy macskát ábrázoló 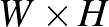$W\times H$ méretű színes képről kell eldöntsük, hogy azon kutya vagy macska szerepel, a neurális háló számára a következőképpen fordítható le: kedves neurális háló, a bemeneti 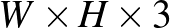$W\times H\times 3$ méretű számtömbre adj kimenetként 0-t, ha a képen kutya található, és 1-et, ha macska. Az alábbiakban ezt az iskolapéldát vesszük górcső alá, ezen keresztül mutatjuk be nagy vonalakban egy neurális háló működését.

Tanulni, tanulni, tanulni

Hogyan oldja meg ezt a feladatot a mesterséges neurális háló, ha sem kutyát, sem macskát nem látott még soha? Nagyon leegyszerűsített értelemben ugyanúgy, mint ahogy a kisgyermek idegrendszerének természetes neurális hálója: ha sokszor lát kutyát/macskát, és ezekre sokszor mondják rá neki, hogy kutya/macska, akkor egy idő után maga is meg tudja különböztetni a kutyaszerű és macskaszerű sajátosságokat. Egy kardinális különbség az, hogy míg a kisgyermeknek mindenféle más napi tevékenységei vannak, és temérdek egyéb dolgot lát (és tanul) a világról, addig az erre a feladatra létrehozott neurális hálót kizárólag ennek a feladatnak az elvégzésére tanítjuk roppant célirányosan. Újra meg újra, több milliószor feleltetjük, ahol egy felelés annyiból áll, hogy beadunk neki egy képet, választ várunk tőle, és visszajelzünk neki, hogy talált-e, vagy sem. Ezt nevezzük felügyelt tanulásnak (supervised learning).

Ez egy kisgyermeknél vélhetőleg hatásos, noha kifogásolható eljárás lenne. Például, ha kétszer egymás után odaadjuk neki ugyanazt a képet, másodjára már jól fog válaszolni. De a neurális háló miért válaszolna másodjára jól? Ugyanarra a bemenetre ugyanazt a kimenetet várnánk egy géptől, bármilyen fejcsóválva is mondtuk neki, hogy elsőre nem talált. Kell valaminek történnie két felelés között, módosítani kell a függvényt! Ezt hogyan kivitelezzük? A neurális háló egy olyan függvény lesz, amelynek kimenete számos, akár sok millió paramétertől függ, ezt a függést a neurális háló általunk megadott szerkezete, architektúrája írja le. Viszont a paraméterek finomhangolását, bizonyos előzetesen rögzített szabályok szerint, bármely két felelés között a háló már automatikusan végzi el az előző felelésen elért eredménye alapján. Emiatt beszélünk gépi tanulásról (machine learning).

Például egy nagyon buta függvény lehetne az, hogy adjunk össze minden pixelintenzitást valamekkora súllyal, és ha ez kisebb, mint 0, akkor legyen 0 a kimenet, egyébként pedig 1. A formulák kedvelőinek, ha a képet a 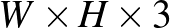$W\times H\times 3$ méretű 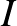$I$ tömbben tároljuk, akkor például az 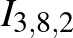$I_{3,8,2}$ szám (értéke 0 és 255 közötti) azt adja meg, hogy a kép 3. sorának 8. oszlopában lévő pixelben a zöld szín intenzitása mekkora (a harmadik, színcsatornát kódoló koordinátában a 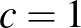$c=1$ a piros, 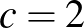$c=2$ a zöld és 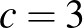$c=3$ a kék színhez tartozik). Az ebből alkotott neurális háló egy 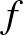$f$ függvény, amely így írható le:

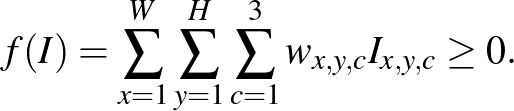
$\displaystyle f(I)=\sum^W_{x=1}\sum^H_{y=1}\sum^3_{c=1}{w_{x,y,c}I_{x,y,c}}\geq 0.$

Ezzel tehát a függvény szerkezetét meghatároztuk, a 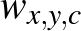$w_{x,y,c}$ súlyok pedig azok a paraméterek, amelyeket felelések között módosít a háló. Ezeket valamilyen módszerrel addig változtatja, amíg a felelések során egyre gyakrabban, vagy egyre nagyobb valószínűséggel jó választ ad. Valójában ez persze önmagában egy rémes szerkezet a fenti célra, amivel a képnek semmilyen jellegzetessége nem ragadható meg jól, de a későbbiekben még vissza fogunk térni rá.

Hogyan módosítsunk?

Még ha a szerkezet stimmel is, nehéz persze úgy módosítani a milliónyi paraméter által leírt bonyolult függvényt, hogy az imént még rossznak ítélt 0 helyett 1-et adjon vissza kimenetként a háló. Ráadásul itt megbújik egy finomság, amire elsőre talán nem gondolnánk, mert olyan példafeladatot választottunk, amiben könnyen ítélünk magabiztosan. De ha mondjuk Ausztriában és Magyarországon készített fényképekről kellene megmondanunk, hogy melyik országban készültek, valószínűleg sokkal többször lennénk bizonytalanok. Hogy járnánk el ekkor egy felelési szituációban? Természetesen tippelnénk a legjobb tudásunk szerint. Bár bizonyára nem nagyon precízen, de mindkét kimenetelnek adnánk valamilyen valószínűséget, és aztán arra tippelnénk, amit valószínűbbnek tartunk. Valójában a neurális háló is a számításai végén egy ilyen valószínűségi kimenetre jut: 64,7%, hogy macska van a képen, 35,3%, hogy kutya.

Az egyik legkiemelkedőbb objektumdetekcióra és -klasszifikációra szolgáló háló, a Mask R-CNN kimenete a bemeneti képre illesztve. A tárgyalt példánál egy komplexebb feladattal megbirkózva a háló megkeresi és beazonosítja a „céltárgyakat”, az adott képen az embereket és a repülőket. Az egyes találatok sarkában lévő számok a tippelt kategóriákhoz tartozó valószínűségek 1-re normálva. Ezek csaknem elérik az 1-et, ami arról árulkodik, hogy ezekben az esetekben a háló magabiztos. (Forrás: https://github.com/matterport/Mask_RCNN.)

Ebben az a jó az előbbi, kategorikus kimenettel szemben, hogy folytonos, bármilyen 0 és 1 (vagy százalékban kifejezve: 0 és 100) közötti értéket felvehet. Így van értelme arról beszélni, hogy egy-egy paraméter apró módosítása mennyiben javítaná vagy rontaná a feleletet, és alkalmas differenciálszámításokat elvégezve – analógiaként gondoljunk a szélsőérték-keresési feladatokra – a háló meg tudja találni azt az optimális módosításhalmazt, ami az adott feleletre a legjobb hatással bír, azt a legközelebb viszi az ideálisan elvárt 0%, 100% (vagy 100%, 0%) kimenethez. Persze mindig csak apró lépéseket téve módosíthatunk, különben elfajuló esetben az új paraméterek teljesen a legfrissebb felelet hatása alá kerülnének, és az azelőtti tapasztalok jelentősége elveszne. Ez az óvatosság például azt is eredményezi, hogy a kisgyermekkel ellentétben, ha egy neurális hálónak ugyanazt a képet kétszer egymásután odaadjuk, könnyen lehet, hogy másodjára is tévedni fog. Ez egyáltalán nem meglepő, ha figyelembe vesszük, hogy nincs is benne olyan alkatrész, ami alapján észrevenné, hogy ugyanazt a képet kapta meg még egyszer! Memóriával csak valamilyen közvetett értelemben rendelkezik, annyira, hogy paramétereinek jelenlegi értékét befolyásolják a korábbi hibái.

Elég ez? Igen, a tapasztalat azt mutatja, hogy ezzel a megközelítéssel lehetséges olyan függvény létrehozása, amely emberi pontossággal oldja meg a feladatot. A betanított neurális háló beépíthető például egy telefonos alkalmazásba, ahol már nem tanul, csak felel, méghozzá kitűnő eredménnyel. Ehhez természetesen kellően reprezentatív tanítóadatra van szükség: ha a tanítás során csak egy-egy kutyás és macskás képből feleltetnénk újra meg újra a neurális hálót, azokat ugyan kiválóan megtanulná, de vélhetőleg csúfosan elbukna egyéb képeken. Ekkor valószínűleg az történne, hogy valójában nem is a képen látható állat alapján osztályozná a képeket, hanem valami egyéb, egyszerűbb jellegzetesség alapján. Ha a kutya a gondozott zöld pázsiton ül, a macska meg egy piros takarón fekszik, a neurális hálóban bizonyára az a sokkal könnyebben tanulható, de sajnos hibás meggyőződés alakulna ki, hogy a „kutyakép” az, amin sok a zöld, a „macskakép” pedig az, amin sok a piros. Ennek megelőzése érdekében a tanítóadatnak a szó szoros és átvitt értelmében is sokszínűnek kell lennie.

A függvény szerkezetének megválasztása: az architektúra

Nehéz és nagyon problémaspecifikus kérdés az, hogy adott feladatot milyen szerkezetű paraméteres függvény – vagy szaknyelven fogalmazva: milyen architektúrájú neurális háló – oldhatna meg a leghatékonyabban. Noha az intuíció szerepe fontos a főbb építőelemek meghatározásában, ezt a kérdést tipikusan nem elmélyült gondolkodás, hanem kitartó kísérletezés alapján tudjuk megválaszolni.

Fentebb leírtunk egy nagyon butának nevezett függvényt. Ez a bemeneti pixelintenzitásokra alkalmazott egy lineáris függvényt, majd ezt összehasonlította a 0 küszöbértékkel. A tanulható paraméterek a lineáris függvény együtthatói voltak. Egyelőre feledkezzünk meg a küszöbről, ez csak a kategóriák véglegesítésére szolgált, és tekintsük csak a lineáris függvényt. Erre úgy gondolunk, mint egyetlen neuronra, ami a bemeneti számok egy lineáris kombinációjának egy eltoltját adja vissza. 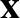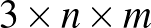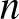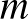Képlettel egy $\mathbf{x}$ bemeneti vektorhoz (amelynek a dimenzióját most tetszőlegesnek tekintjük, a képfeldolgozás példájában ez $3\times n\times m$ volt, ahol $n$ és $m$ azt jelenti, hogy a képen hány sorban és oszlopban voltak a pixelek, azaz akár százezres nagyságrendű is lehet a koordináták száma a vektorban) a 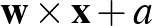$\mathbf{w}\times \mathbf{x}+a$ számot rendeli hozzá, ahol a 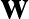$\mathbf{w}$ ugyanolyan hosszú vektor, mint 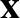$\mathbf{x}$ , a szorzás skalárszorzatot jelent (azaz összeszorozzuk a megfelelő koordinátákat, majd ezeket a számokat összeadjuk), a pedig egy szám. Az alábbi ábrán egy ilyen neuron sematikus rajza látható.

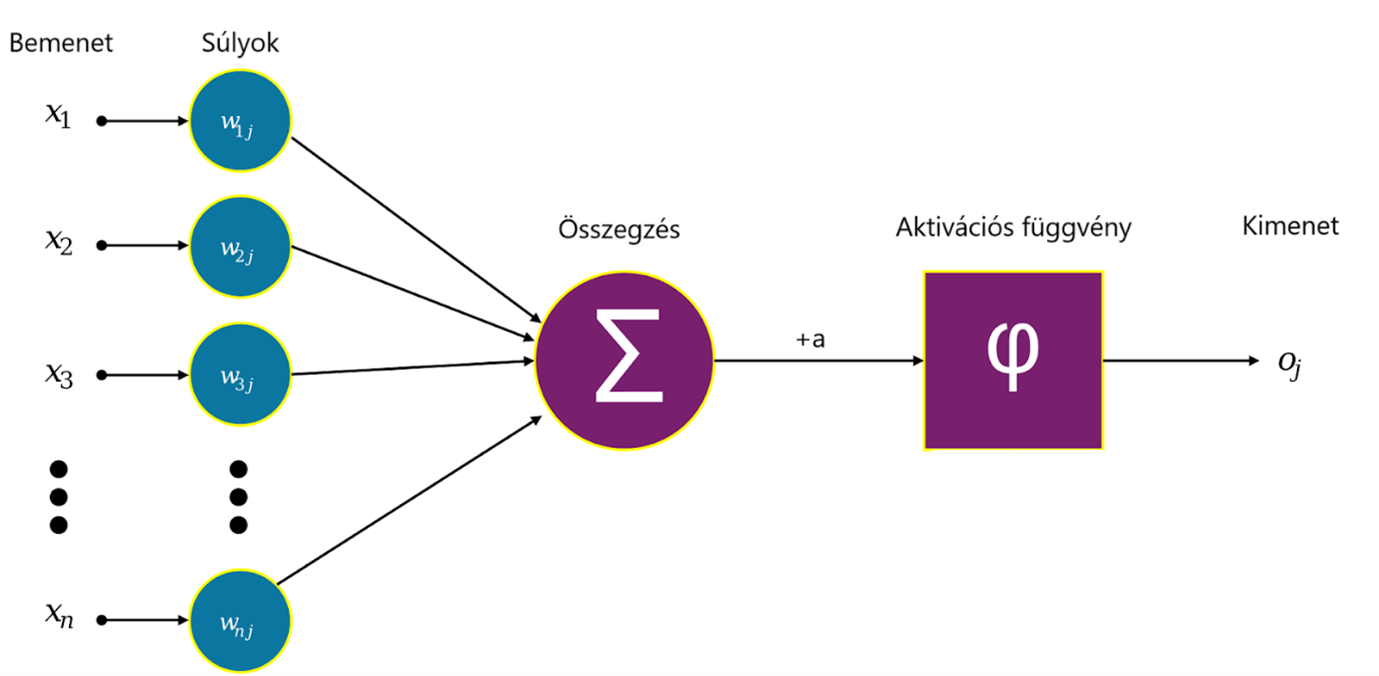
Egy mesterséges neuron struktúrája. (Forrás: Wikipédia.)

Egy neurális háló temérdek ilyen neuronból áll, amelyek rétegekbe tömörülnek. Az első, bemeneti réteg neuronjainak az eredeti bemeneti kép pixelintenzitásai jelentik a bemenetet, ezekből számol ki mindegyikük egy saját kimenetet. Ha a fenti 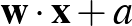$\mathbf{w}\cdot\mathbf{x}+a$ számokat kiszámoljuk a rétegben lévő összes neuronra és ezeket egy vektorba rendezzük mint koordinátákat, akkor az első réteg kimenete 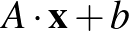$A\cdot\mathbf{x}+b$ alakban írható, ahol 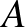$A$ egy mátrix (sorai az egyes neuronok 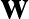$\mathbf{w}$ vektorai), 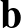$\mathbf{b}$ pedig egy vektor, koordinátái az egyes neuronokhoz tartozó 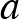$a$ számok. Ezek a kimeneti értékek szolgálnak bemenet gyanánt a második réteg neuronjainak, és így tovább, egészen az utolsó, kimeneti rétegig, amely a neurális háló egészének kimenetét adja vissza. A köztes rétegek az úgynevezett rejtett rétegek. Egy csúcskategóriás képfelismerő háló több száz ilyen réteget is tartalmaz, rajtuk összesen százmilliós nagyságrendű hangolható paraméterrel. A rétegek nagy számából ered a divatos mélytanulás – deep learning kifejezés. Egy ilyen típusú neurális hálót, amiben nincsenek visszacsatolások, azaz minden neuron csak egyszer végez számítást egy bemenet feldolgozása során, előrecsatoltnak (feed-forward) nevezünk.

Fentebb nem voltunk precízek. Hiszen lineáris függvények kompozíciója is lineáris, mi értelme van akár csak két egymást követő neuronnak, nemhogy több száz rétegnyinek... Ahhoz, hogy valami nemtriviális kisüljön ebből a felépítésből, minden neuron mögé be van építve egy úgynevezett aktivációs függvény, ami nemlineáris. Méghozzá gyakran szemtelenül egyszerűen nem az: az egyik legnépszerűbb aktivációs függvény az úgynevezett 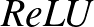$ReLU$ (rectified linear unit) függvény, amely a következő képlettel írható le:

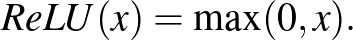
$\displaystyle ReLU(x)=\max_{}(0,x).$

Azaz a neuron kiszámítja a bemeneteinek általa használt lineáris függvényét, és ha az eredmény pozitív, akkor ebben a formában tovább is adja, ha pedig nem, akkor 0-t ad tovább. Képlettel felírva, egy 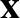$\mathbf{x}$ bemeneti vektorhoz egy neuronréteg által adott kimenet 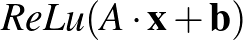$ReLu(A\cdot\mathbf{x}+\mathbf{b})$ . Ez már kinyitja a világot: az univerzális approximáció tétele szerint tetszőleges függvény közelíthető neurális hálókkal, amelyben 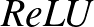$ReLU$ aktivációval ellátott neuronok rétegei követik egymást. E tétel természetesen elsősorban matematikai érdekesség, semmint praktikus áttörés, de nagyon jól érzékelteti, hogy egészen kevés nemlinearitás mennyire meg tud bolygatni egy egyszerű rendszert. A 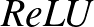$ReLU$ gyakorlati jelentőségét ugyanakkor az adja, hogy praktikus problémákban is rendkívül hatékonynak bizonyul. Analógiaként érdemes megemlíteni az egyetemi tanulmányokból a Taylor-polinomot, ami szintén képes bonyolult függvényeket, például exponenciális vagy trigonometrikus függvényeket, közelíteni annak ellenére, hogy ő maga „csak” polinom, azaz mindössze szorzásokat és összeadásokat tartalmaz. Az analógia a neurális háló újszerűségére is segít rávilágítani. Míg a Taylor-polinom esetében egy ismert képletű függvényt, például 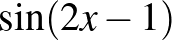$\sin(2x-1)$ szeretnénk polinommal közelíteni – akár csak azért, hogy az értékét egy adott 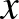$x$ -re (legalább közelítőleg) kiszámítsuk –, addig a neurális háló egy olyan függvényt közelít, aminek a képletét nem ismerjük. A kutya/macska megkülönböztetés esetében x egy képet reprezentál, ami egy akár százezer koordinátából álló vektor, a kimenet pedig 0 vagy 1 aszerint, hogy kutya vagy macska van a képen. Természetesen ezt a függvényt senki nem ismeri, mindössze annyit tudunk, hogy képek százaira, vagy ezreire ismerjük, hogy 0 vagy 1 kimenet tartozik-e hozzájuk. Ezeket a képeket beadhatjuk bemenetként egy neurális hálónak, amely 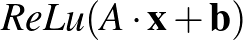$ReLu(A\cdot\mathbf{x}+\mathbf{b})$ alakú függvények egymás utáni alkalmazását jelenti, és megfelelő algoritmussal rábírjuk arra, hogy az A mátrixban és a b vektorban szereplő számokat úgy állítsa be, hogy az általunk kívánt kimenetet adja.

Még egy fontos és egyszerű architekturális megjegyzést szeretnénk tenni. A fentiek alapján minden neuron az előző réteg összes neuronjával össze van kötve, illetve a bemeneti réteg neuronjai az összes bemeneti pixelből számolják ki a maguk kimenetét, azaz az A mátrix lényegében minden eleme nem 0. A példafeladatunkban nagyon rossz kezdés, ha így esünk neki a bemeneti képnek,; a neuronok nem is vesznek tudomást a kép egyes pixeleinek geometriai viszonyáról. Olyan, mintha kezdés előtt minden képen összekevernénk az összes pixelt egy előre adott módon, és a hálót így próbálnánk tanítani. Az elvi lehetőség persze így is megvan arra, hogy a háló idővel rátalál a megfelelő súlyokra, de ez ebben a formában gyakorlatilag kivitelezhetetlen. A tanítás működőképességének egyik kulcsa annak észrevétele, hogy a geometriai viszonyrendszert érdemes a háló rétegeiben is megőrizni: például az első réteg neuronjai rendre feleljenek a bemeneti kép pixeleinek, és egy-egy neuron csak a nagyon szűk, mondjuk 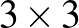$3\times 3$ -as környezetében lévő pixelek intenzitását vegye be bemenetként, azaz az A mátrix speciális szerkezetű, rengeteg eleme 0. Ez a gondolat vezet el minket a képfeldolgozás területét 2010 körül forradalmasító konvolúciós neurális hálókhoz. Vegyük azt is észre, hogy a kapcsolatok megnyírbálásával a paraméterek száma is drasztikusan csökken, a fenti példában az első rétegbeli neuronjaink által hordozott lineáris függvényeket 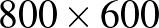$800\times 600$ helyett 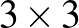$3\times 3$ súly megadásával specifikálhatjuk.

Képosztályzás mesterfokon

A fent megoldott feladat banálisnak és mondvacsináltnak is tűnhet, és talán az sem nyűgöz le minket túlzottan, hogy a gép emberi pontosságot ér el rajta. A fenti módszerek segítségével azonban olyan képosztályzási feladatokra is taníthatók hatékony konvolúciós neurális hálók, amelyek nagyon is húsbavágók, és egy átlagember teljesen eszköztelen velük szemben. Talán a legpompásabb példa az orvosi képek (röntgenfelvétel, CT, MR) osztályozása aszerint, hogy a képen látható szerven milyen betegségek figyelhetők meg (például az adott mellkasi CT-n látható-e rákos elváltozás). Ez egy olyan kérdés, amelynek megválaszolására csak speciálisan képzett szakemberek, radiológusok alkalmasak, méghozzá meglehetősen sok munka árán. Egy CT-felvétel például egy háromdimenziós kép, amelyre legegyszerűbb úgy gondolni, mint többszáz egymásra pakolt röntgenfelvételre. Egy ilyen képen korai stádiumú, csak kevés voxelt (a pixel háromdimenziós megfelelője) érintő rákos elváltozások megkeresése igen fáradságos feladat. Ebből könnyen belátható, hogy a széleskörű szűrések elvégzésében a képzett szakemberek munkaórái is szűk keresztmetszetnek bizonyulhatnak. Éppen ezért elvitathatatlan jelentőséggel bír, hogy gépi tanulás révén olyan automatizált eszközöket tudunk létrehozni, amelyek a képek hadának minél gyorsabb áttekintésében segítik őket.

Zárókép

A fentiekben – bár nem bocsátkoztunk mélyebb részletekbe – bemutattuk, hogyan működik egy képeket osztályozó mély neurális háló, mit értünk ennek felügyelt tanítása alatt, és milyen elemekből épül fel egy előrecsatolt neurális háló. A felhasznált példafeladatra ezek a bevett megközelítések. Ugyanakkor vannak olyan problémák, amelyek gyökeresen eltérő módszertant igényelnek. Például a Google Deepmind által 2017-ben fejlesztett, mesterséges intelligencia alapú AlphaZero rendkívül egyoldalú mérkőzesen győzte le az akkor legerősebb klasszikus sakkprogramot, a Stockfish-t. Noha az összecsapás technikai feltételeit érték kritikák, az AlphaZero forráskódja alapján készült Leela Chess Zero a sakkprogramok 2019-es bajnokságának döntőjében egyenlőnek elismert feltételek mellett is felülmúlta a Stockfish-t egy kiélezett összecsapáson. Ebből már magunk is sejthetjük, hogy az AlphaZero nem felügyelt tanulásban részesült, nem az történt, hogy kapott temérdek állást, amire meg kellett mondania a „legjobb ismert” lépést, hiszen akkor nemigen kerekedhetett volna felül a legjobb ismert lépéseket szolgáltató korábbi megközelítéseken. Ehelyett megerősítéses tanulással (reinforcement learning) lett betanítva, ami egy rendkívül érdekes, de a terjedelmi kereteinken túlmutató gépi tanulási paradigma. Ennek keretében a gép önmagával játszik elképesztő mennyiségű sakkpartit, és így a saját bőrén tapasztalja meg, hogy adott helyzetekben merre érdemes alakítania az állást, ha nyerni akar. Ezáltal az AlphaZero korábbi emberi játszmákra nem jellemző stratégiai motívumokat is felfedezett, amelyekből bizonyos elemeket a sakknagymesterek is átvettek. Ennek szépségét nem lehet eltúlozni: olyan jól tanítottuk a neurális hálót, hogy már mi tanulunk tőle. Lehet-e ennél nagyobb öröme a mesternek?

Maga Balázs,
HUN REN Rényi Alfréd Matematikai Kutatóintézet

Simon L. Péter,
ELTE TTK Alkalmazott Analízis és Számításmatematikai Tanszék

Információk

Főmenü