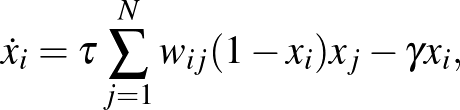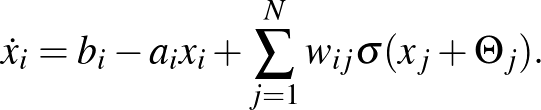Bevezetés
Az amerikai John J. Hopfieldnek és a kanadai Geoffrey E. Hintonnak ítélték oda 2024-ben a fizikai Nobel-díjat – jelentették be október elején Stockholmban a Svéd Királyi Akadémián. A két kutató úttörő eredményeivel jelentősen hozzájárult a gépi tanulás lehetővé tételéhez mesterséges neurális hálózatokkal.
 Hopfield a 80-as évek elején hozta létre és vizsgálta a ma már Hopfield-hálózatnak nevezett matematikai modellt. Erről az elmúlt évtizedekben kiemelkedően sok tudományos publikáció született. Hopfield kiinduló cikkét mintegy tízezren idézik tudományos publikációkban, de a témával foglalkozó dolgozatok száma ennél sokkal több. A Hopfield-hálózatról már a nagy nyelvi modellek is tudnak ismertetőt írni, az alábbi például itt érhető el:
Hopfield a 80-as évek elején hozta létre és vizsgálta a ma már Hopfield-hálózatnak nevezett matematikai modellt. Erről az elmúlt évtizedekben kiemelkedően sok tudományos publikáció született. Hopfield kiinduló cikkét mintegy tízezren idézik tudományos publikációkban, de a témával foglalkozó dolgozatok száma ennél sokkal több. A Hopfield-hálózatról már a nagy nyelvi modellek is tudnak ismertetőt írni, az alábbi például itt érhető el:
AI generated definition based on: Quantum Inspired Computational Intelligence, 2017:
A Hopfield Network is a type of recurrent content-addressable memory in computer science. It is a fully autoassociative architecture with symmetric weights and binary threshold nodes. This network has the ability to transform itself through transitions to different states until it stabilizes. The weights between the nodes enforce constraints that influence the outputs of the network.
Az Olvasó a fordítást is elkészítheti valamelyik mesterséges intelligencia algoritmust alkalmazó nyelvi modellel. Bár a fordítás elkészítése után is megmaradhat a hiányérzetünk, valójában mi is a Hopfield-hálózat, tudjuk-e meglevő matematikai ismereteinkhez kötni valahogy. Jelen cikk megpróbál egy matematikán nevelődött, gondolkodó, és kis időt, energiát erre rászánó olvasónak ehhez némi szellemi muníciót adni.
Hálózatok és gráfok
A hálózat matematikai szakszóval egy gráf, amely csúcsokból és élekből áll, első példaként Euler königsbergi hidait szoktuk emlegetni. Ebben a példában a gráfot le tudjuk rajzolni, a csúcsokat pontok, az éleket ezeket összekötő vonalak jelzik. Nagy gráfoknál, mint az internet, vagy az agy, ez a reprezentáció kevéssé alkalmazható, de az elvont fogalom ott is működik: a gráf két halmaz megadását jelenti, az egyik a csúcsok halmaza, gyakran 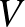 jelöli (angolul a csúcs=vertex) a másik pedig az élek
jelöli (angolul a csúcs=vertex) a másik pedig az élek 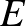 halmaza (edge), amely
halmaza (edge), amely  egy részhalmaza, azaz olyan csúcspárokból áll, amelyek össze vannak kötve. Nagy hálózatok esetében nem feltétlenül tartjuk számon, hogy egy csúcs pontosan mely másik csúcsokkal van összekötve, hanem valamilyen tulajdonságú véletlen gráfokkal reprezentáljuk a hálózatot. A véletlen gráfok vizsgálata Erdős Pál és Rényi Alfréd meghatározó dolgozatával kezdődött.
egy részhalmaza, azaz olyan csúcspárokból áll, amelyek össze vannak kötve. Nagy hálózatok esetében nem feltétlenül tartjuk számon, hogy egy csúcs pontosan mely másik csúcsokkal van összekötve, hanem valamilyen tulajdonságú véletlen gráfokkal reprezentáljuk a hálózatot. A véletlen gráfok vizsgálata Erdős Pál és Rényi Alfréd meghatározó dolgozatával kezdődött.
A számítógépek felgyorsulása lehetőséget teremtett a nagy hálózatok kísérleti vizsgálatára is, ami a hálózatelmélet 2000-es évek eleji elterjedését tette lehetővé. Ennek gyakran idézett mérföldköve a Barabási−Albert-féle hálózati modell megalkotása volt.
Folyamatok hálózatokon
A fentiekben a hálózat matematikai reprezentációját mutattuk be, most továbblépünk, a hálózaton végbemenő folyamat matematikai leírása felé.
A hálózatot adottnak tekintjük, de a csúcsai különböző állapotokban lehetnek. A gráfelméletben ezt a gráf csúcsai színezésének is nevezzük, de a különböző alkalmazások nem színeket használnak. Az egyik kézenfekvő alkalmazás a fertőzésterjedés modellezése, ekkor a gráf csúcsai például két állapotúak lehetnek: egészséges és fertőzött. (Komolyabb modelleknél a betegség több állapottal írható le, lehetnek gyógyultak, akik már nem fertőzhetők meg, vagy fertőzöttek, akik még a betegség szimptómáit nem mutatják.) Az információ vagy hírek terjedése esetében lehetnek olyan csúcsai a gráfnak, amelyek azokat reprezentálják, akik még nem tudják a hírt, lehetnek olyanok, akik tudják és terjesztik, illetve olyanok, akik tudják, de már nem terjesztik. Neuronok hálózatában lehetnek aktív és inaktív csúcsok. Általánosságban a gráf mellett adott egy dinamika, amely egyrészt azt adja meg, hogy melyek egy csúcs lehetséges állapotai, másrészt azt, hogy a különböző állapotok között milyen szabályok szerint változik egy csúcs állapota. Ismét a fertőzés terjedését használva példaként: egy egészséges csúcs beteggé válhat, ennek az átmenetnek a bekövetkezése a fertőzött szomszédok számától függ valamilyen képlet szerint, illetve egy beteg csúcs meggyógyulhat, ez rendszerint független a szomszédos csúcsok állapotától.
Közel vagyunk ahhoz, hogy a fentieket képletek formájában is leírjuk, azaz matematikai modellt mutassunk be. Még elég sok szabadságunk van (lenne) a konkrét formába öntéshez, de elköteleződünk egy olyan formalizmus mellett, amely elegendően általános ahhoz, hogy egy összetett jelenséget leírjon, és ezzel egyidejűleg elég egyszerű ahhoz, hogy kezelhető legyen. (A kezelhető nem csak arra vonatkozik, hogy ezen cikk olvasóját ne riassza el, hanem arra is, hogy a szakemberek sikeresen vizsgálni tudják a matematika általánosan ismert eszközeivel.) Ez a formalizmus azt feltételezi, hogy egy csúcs állapotát egyetlen számmal jellemezni tudjuk, ezt az egyes számú csúcs esetében 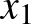 , a kettes csúcs esetében
, a kettes csúcs esetében 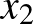 , az
, az 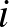 -edik csúcs esetében
-edik csúcs esetében 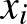 jelöli. Ráadásul ez a szám időben változhat, tehát valójában az
jelöli. Ráadásul ez a szám időben változhat, tehát valójában az 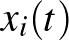 jelölés adja meg az
jelölés adja meg az 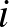 -edik csúcs állapotát a
-edik csúcs állapotát a 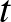 időpontban, azaz
időpontban, azaz 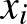 nem is egy szám, hanem egy számértékű függvény. Ismét a fertőzésterjedés példájára utalva,
nem is egy szám, hanem egy számértékű függvény. Ismét a fertőzésterjedés példájára utalva, 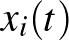 jelölheti annak valószínűségét, hogy az
jelölheti annak valószínűségét, hogy az 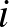 -edik csúcs a
-edik csúcs a 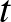 időpontban fertőzött. Neuronok esetében
időpontban fertőzött. Neuronok esetében 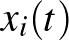 jelölheti az
jelölheti az 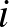 -edik neuron tüzelési rátáját a
-edik neuron tüzelési rátáját a 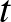 időpontban.
időpontban.
Hálózati folyamat differenciálegyenlete
Elérkeztünk a legkritikusabb pillanathoz, valamilyen törvényszerűséget kell felírnunk a fenti függvények megváltozásának leírására. (Ahogy az ismert filmből tudjuk: „a nemzetközi helyzet egyre fokozódik”.) Elővesszük a változások matematikai modellezésének ősi eszközét, a differenciálegyenletet. (Egy pillanatra megállva nem hagyhatjuk ki annak megemlítését, hogy bár az eszközt a 17. században fejlesztették ki, és azóta meghatározó szerepet játszott az emberiség technikai fejlődésében, a matematika érettségi küszöbén nem tört át, ezért kevesen tudnak a létezéséről. Ha esetleg felmerül az Olvasóban, hogy ezen cikk az áttörés érdekében végzett lobbitevékenység része, akkor szeretnénk biztosítani, hogy nem így van. Meggyőződésem szerint a differenciálegyenleteken 18-as karika van, az egyetemi tanulmányok során érik meg rá az ember, ahogy talán a középiskolai fizika, biológia, történelem tanulmányainkban előkerülő számos témára, nem is szólva az élettapasztalatot igénylő mély irodalmi művek megértéséről.)
A differenciálegyenlet egy függvény megváltozását jellemző mennyiségére, a deriváltjára ad képletet. A mi 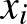 függvényünkre számos modell általánosításaként a következő írható fel:
függvényünkre számos modell általánosításaként a következő írható fel:

ahol a bal oldalon a függvény feletti pont a deriváltját jelöli, a jobb oldalon pedig a következő jelöléseket használtuk. Az 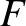 függvény azt írja le, hogy egy csúcs állapota önmagában (a szomszédaitól függetlenül) hogyan változik. A
függvény azt írja le, hogy egy csúcs állapota önmagában (a szomszédaitól függetlenül) hogyan változik. A 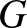 függvény azt mutatja meg, hogy a
függvény azt mutatja meg, hogy a 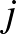 -edik csúcs állapota milyen hatással van az
-edik csúcs állapota milyen hatással van az 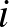 -edik csúcs állapotára. A
-edik csúcs állapotára. A  valójában egy mátrix (azaz egy táblázat), amelyben az
valójában egy mátrix (azaz egy táblázat), amelyben az 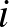 -edik sor
-edik sor 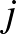 -edik eleme
-edik eleme 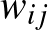 adja meg, hogy az
adja meg, hogy az 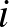 -edik és
-edik és 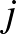 -edik csúcs össze van-e kötve, azaz ebben van kódolva a hálózat. Legegyszerűbb esetben ennek értéke 1, ha a csúcsok össze vannak kötve, vagy 0, ha nincsenek összekötve. De lehet más szám is, ha azt is jellemezni akarjuk, hogy mennyire erős a csúcsok közötti kapcsolat. Ez például neuronok hálózatában jelentős, innen származik a
-edik csúcs össze van-e kötve, azaz ebben van kódolva a hálózat. Legegyszerűbb esetben ennek értéke 1, ha a csúcsok össze vannak kötve, vagy 0, ha nincsenek összekötve. De lehet más szám is, ha azt is jellemezni akarjuk, hogy mennyire erős a csúcsok közötti kapcsolat. Ez például neuronok hálózatában jelentős, innen származik a 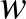 jelölés, ami az összekötés súlyára utal. Végül a jobb oldalon álló szumma jel azt fejezi ki, hogy az egyes csúcsokból jövő hatást összegezni kell, ebben a
jelölés, ami az összekötés súlyára utal. Végül a jobb oldalon álló szumma jel azt fejezi ki, hogy az egyes csúcsokból jövő hatást összegezni kell, ebben a 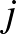 a futó index, azaz
a futó index, azaz 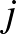 a hálózat összes csúcsán végigmegy.
a hálózat összes csúcsán végigmegy.
Érdemes néhány konkrét modellt megnéznünk, amelyek alátámasztják a fenti általános egyenlet létjogosultságát.
Az első a járványterjedés (egyik lehetséges) modellje hálózaton.
ebben a csúcsok állapotát megadó 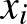 függvény az
függvény az 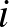 -edik csúcs fertőzöttségének valószínűsége. A fenti általános modell
-edik csúcs fertőzöttségének valószínűsége. A fenti általános modell 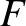 függvénye
függvénye 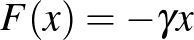 , ahol
, ahol 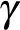 jelöli az úgynevezett gyógyulási rátát, ami azt jellemzi, hogy átlagosan mennyi időt tölt valaki a fertőzött állapotban. A negatív előjel azt fejezi ki, hogy a fertőzöttek fokozatosan elhagyják ezt az állapotot, és visszatérnek az egészséges állapotba. Az általános modell
jelöli az úgynevezett gyógyulási rátát, ami azt jellemzi, hogy átlagosan mennyi időt tölt valaki a fertőzött állapotban. A negatív előjel azt fejezi ki, hogy a fertőzöttek fokozatosan elhagyják ezt az állapotot, és visszatérnek az egészséges állapotba. Az általános modell 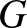 függvénye
függvénye 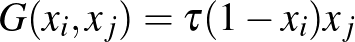 , kifejezve azt, hogy az
, kifejezve azt, hogy az 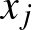 fertőzöttségi, és
fertőzöttségi, és 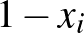 egészségességi valószínűség szorzata adja annak valószínűségét, hogy a
egészségességi valószínűség szorzata adja annak valószínűségét, hogy a 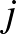 -edik csúcs megfertőzi az
-edik csúcs megfertőzi az 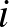 -ediket, ebben a
-ediket, ebben a 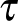 paraméter a fertőzési ráta a fertőzés erősségét jellemzi, de ebbe épül be például az is, ha a maszk viselése miatt kevésbé fertőzik egymást az egyedek.
paraméter a fertőzési ráta a fertőzés erősségét jellemzi, de ebbe épül be például az is, ha a maszk viselése miatt kevésbé fertőzik egymást az egyedek.
Szintén belefér az általános modell kereteibe a a címben is említett Hopfield- vagy Cowan–Wilson-modell:
Ebben 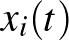 az
az 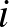 -edik neuron aktivitását adja meg a
-edik neuron aktivitását adja meg a 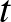 időpontban. A fenti általános modell
időpontban. A fenti általános modell 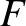 függvénye
függvénye 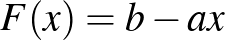 , ahol
, ahol 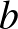 a neuront érő külső (hálózaton kívüli) hatás, az
a neuront érő külső (hálózaton kívüli) hatás, az 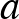 paraméter pedig azt jellemzi, hogy milyen gyorsan tér vissza a neuron a gerjesztettből a nyugalmi állapotba (erre utal ismét a negatív előjel). A szumma jel ismét az egyes neuronok hatásának összegzését jelenti, mögötte pedig a modell
paraméter pedig azt jellemzi, hogy milyen gyorsan tér vissza a neuron a gerjesztettből a nyugalmi állapotba (erre utal ismét a negatív előjel). A szumma jel ismét az egyes neuronok hatásának összegzését jelenti, mögötte pedig a modell 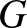 függvénye van. Ebben a
függvénye van. Ebben a 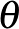 egy küszöbértéket jelöl, amelyet el kell érnie a neuronnak, hogy egy másikat aktiválni tudjon, a
egy küszöbértéket jelöl, amelyet el kell érnie a neuronnak, hogy egy másikat aktiválni tudjon, a 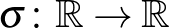 függvény pedig a hatás erősségét kifejező úgynevezett szigmoid függvény, amely növekedő, de végtelenben véges határértéke van. Ilyen függvények általában exponenciális növekedés után telítődést fejeznek ki, tipikusan megjelennek gazdasági vagy demográfiai modellekben is, kifejezve azt, hogy a kezdeti exponenciális növekedést mindig telítődést követi, azaz lelassul a növekedés, és egy konstans érték áll be („a fák nem nőnek az égig”, és a legújabb típusú okostelefon eladási számai is csak egy darabig növekednek exponenciálisan).
függvény pedig a hatás erősségét kifejező úgynevezett szigmoid függvény, amely növekedő, de végtelenben véges határértéke van. Ilyen függvények általában exponenciális növekedés után telítődést fejeznek ki, tipikusan megjelennek gazdasági vagy demográfiai modellekben is, kifejezve azt, hogy a kezdeti exponenciális növekedést mindig telítődést követi, azaz lelassul a növekedés, és egy konstans érték áll be („a fák nem nőnek az égig”, és a legújabb típusú okostelefon eladási számai is csak egy darabig növekednek exponenciálisan).
Különböző fajok populációinak együttélését írja le az általánosított Lotka–Volterra-modell. (Egy ragadozó és zsákmány faj kölcsönhatására fejlesztették ki eredetileg a 20. század elején a Lotka–Volterra-féle modellt, amely először írt le periodikus viselkedést egy biológiai rendszerben.) A modell szintén a fenti általános egyenlet formájába írható:
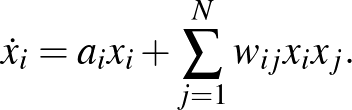
Ebben  az
az  -edik faj populációjának méretét jelöli. A
-edik faj populációjának méretét jelöli. A 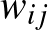 számok negatívak is lehetnek. Ha
számok negatívak is lehetnek. Ha 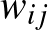 és
és  is pozitív, akkor a két faj segíti egymást, szimbiózisban élnek, ha mindkettő negatív, akkor versengőnek nevezzük a fajokat, ha pedig az egyik pozitív, a másik negatív, akkor ragadozó–zsákmány viszony van köztük. Megjegyezzük, hogy ha reálisabb („a fák nem nőnek az égig” típusú) modellt szeretnénk, akkor az
is pozitív, akkor a két faj segíti egymást, szimbiózisban élnek, ha mindkettő negatív, akkor versengőnek nevezzük a fajokat, ha pedig az egyik pozitív, a másik negatív, akkor ragadozó–zsákmány viszony van köztük. Megjegyezzük, hogy ha reálisabb („a fák nem nőnek az égig” típusú) modellt szeretnénk, akkor az 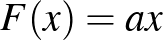 függvény helyett célszerű az
függvény helyett célszerű az 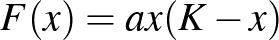 függvényt használni, amelyben a
függvényt használni, amelyben a  paramétert eltartó képességnek nevezik, ez határozza meg a populáció méretét, ha más fajok nincsenek jelen.
paramétert eltartó képességnek nevezik, ez határozza meg a populáció méretét, ha más fajok nincsenek jelen.
Érdekességképpen, illetve a modell általános alkalmazhatóságának illusztrálásra megemlítjük a Kuramoto-modellt is

amely biológiában, kémiában és idegtudományban vizsgált oszcilláló rendszerek viselkedését modellezi. Ebben 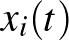 az
az 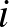 -edik oszcillátor aktivitása a
-edik oszcillátor aktivitása a 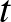 időpontban,
időpontban, 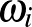 ennek saját rezgését leíró paraméter,
ennek saját rezgését leíró paraméter,  pedig az összekötés erősségét jellemző, meghatározó szerepet játszó paraméter. Kuramoto a 70-es, 80-as években teljesen összekötött hálózat esetében megmutatta, hogy a
pedig az összekötés erősségét jellemző, meghatározó szerepet játszó paraméter. Kuramoto a 70-es, 80-as években teljesen összekötött hálózat esetében megmutatta, hogy a  értékét növelve egy adott ponton hirtelen megjelenik az oszcillátorok szinkronizációja, ami később számos helyen feltűnt a tudomány különböző területein. Azóta a legegyszerűbb teljes gráf mellett számos más hálózat esetében vizsgálták a szinkronizáció létrejöttét.
értékét növelve egy adott ponton hirtelen megjelenik az oszcillátorok szinkronizációja, ami később számos helyen feltűnt a tudomány különböző területein. Azóta a legegyszerűbb teljes gráf mellett számos más hálózat esetében vizsgálták a szinkronizáció létrejöttét.
Neurális hálók
Térjünk vissza a cikk elején említett neurális hálókra és azok tanítására. Hopfield meghatározó jelentőségű eredménye a fenti differenciálegyenlettel kapcsolatban annak igazolása, hogy szimmetrikus  súlymátrix esetén a megoldások egyenensúlyi pontokhoz tartanak. A rendszernek számos egyensúlyi pontja lehet, amelyek megfelelhetnek a memóriában tárolt emlékeknek. Adott kezdeti feltételből indítva a megoldást, valamelyik egyensúlyi állapothoz tart, amit úgy is interpretálhatunk, hogy a neurális háló egy adott bemenetre felidézi valamelyik emlékképet. Ezen a ponton érdemes a differenciálegyenletekről áttérni az időben nem folytonosan, hanem lépésenként haladó (azaz időben diszkrét) egyenletekre, amelyekben az
súlymátrix esetén a megoldások egyenensúlyi pontokhoz tartanak. A rendszernek számos egyensúlyi pontja lehet, amelyek megfelelhetnek a memóriában tárolt emlékeknek. Adott kezdeti feltételből indítva a megoldást, valamelyik egyensúlyi állapothoz tart, amit úgy is interpretálhatunk, hogy a neurális háló egy adott bemenetre felidézi valamelyik emlékképet. Ezen a ponton érdemes a differenciálegyenletekről áttérni az időben nem folytonosan, hanem lépésenként haladó (azaz időben diszkrét) egyenletekre, amelyekben az 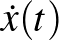 derivált helyett az
derivált helyett az 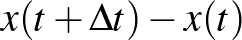 különbség szerepel. (A
különbség szerepel. (A 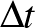 nevezővel átszorzunk a jobb oldalra, és beépítjük az ott szereplő függvényekbe.) Ez lehetővé teszi, hogy az
nevezővel átszorzunk a jobb oldalra, és beépítjük az ott szereplő függvényekbe.) Ez lehetővé teszi, hogy az 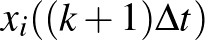 értékét az egyenlet alapján kiszámítsuk az
értékét az egyenlet alapján kiszámítsuk az 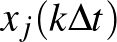 értékekből. Ha a
értékekből. Ha a 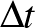 értéket választjuk időegységnek, akkor az egyszerűbb
értéket választjuk időegységnek, akkor az egyszerűbb 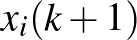 és
és  jelöléseket használjuk. Az egyszerűség kedvéért speciális
jelöléseket használjuk. Az egyszerűség kedvéért speciális 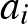 és
és 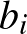 értékeket választva, az (1) egyenletből az
értékeket választva, az (1) egyenletből az
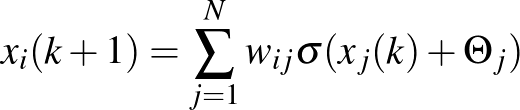
diszkrét idejű egyenletet kapjuk. Bevezetve az 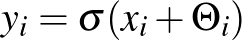 jelölést, az egyenlet az
jelölést, az egyenlet az 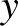 változókra így írható:
változókra így írható:
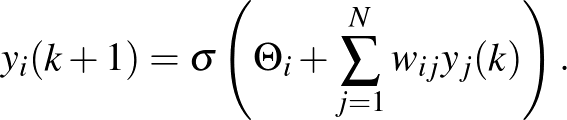
A képlet még tömörebb formába hozható, ha vektoriális jelölést használunk, az 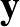 vektor koordinátái lesznek az
vektor koordinátái lesznek az 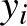 számok, hasonlóképpen a
számok, hasonlóképpen a  jelenti a
jelenti a  értékekből álló vektort, és
értékekből álló vektort, és  lesz a
lesz a 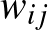 súlyokból álló mátrix. Ekkor a Hopfield-modell jobban elterjedt alakjához jutunk:
súlyokból álló mátrix. Ekkor a Hopfield-modell jobban elterjedt alakjához jutunk:

Ebben a kontextusban a memóriából egy emlék előhívása azt jelenti, hogy kiindulunk egy 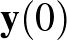 vektorból, és a fenti iterációt addig folytatjuk, amíg az
vektorból, és a fenti iterációt addig folytatjuk, amíg az 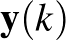 már nem változik, azaz valójában konvergál egy
már nem változik, azaz valójában konvergál egy  vektorhoz. Ez a vektor természetesen teljesíti az
vektorhoz. Ez a vektor természetesen teljesíti az

egyenletet.
Az ilyen neurális hálókat rekurrensnek nevezik, mert elvileg soha nem ér véget az iteráció, csak konvergál(hat) egy értékhez. Befejezésül megmutatjuk a gyakrabban használt előremenő (feed-forward) hálókat, amelyeket a mélytanulás (deep-learning) során is használnak.
A feed-forward hálók kapnak egy bemenetet és véges sok lépésben (a fent említett rekurrens hálókkal ellentétben, amelyek „örökké” futnak) egy kimenetet adnak. Jelölje a bemenetet, ami egy vektor,  . Először egy úgynevezett egy rétegű hálót mutatunk, ami lényegében egy speciális alakú függvény. A függvény megadásához három dolog szükséges: egy
. Először egy úgynevezett egy rétegű hálót mutatunk, ami lényegében egy speciális alakú függvény. A függvény megadásához három dolog szükséges: egy 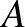 mátrix, egy
mátrix, egy 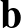 vektor és egy egyváltozós függvény,
vektor és egy egyváltozós függvény, 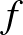 . Az egyrétegű neurális háló az
. Az egyrétegű neurális háló az
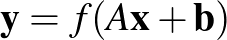
függvény, amelynek kimenete  . A jelölés magában foglalja azt, hogy az egyváltozós
. A jelölés magában foglalja azt, hogy az egyváltozós 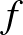 függvényt az argumentumában álló vektorra koordinátánként alkalmazzuk. A függvény gyakran a fent említett szigmoid típusú függvény, de kiderült, és a mélyhálókban gyakran azt alkalmazzák, hogy az
függvényt az argumentumában álló vektorra koordinátánként alkalmazzuk. A függvény gyakran a fent említett szigmoid típusú függvény, de kiderült, és a mélyhálókban gyakran azt alkalmazzák, hogy az 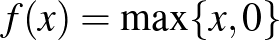 , röviden
, röviden 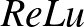 (rectified linear unit) is hatékonyan alkalmazható a gépi tanulás során. Megjegyezzük, hogyha ezt alkalmazzuk, akkor a kimenet szakaszonként lineáris függvénye a bemenetnek.
(rectified linear unit) is hatékonyan alkalmazható a gépi tanulás során. Megjegyezzük, hogyha ezt alkalmazzuk, akkor a kimenet szakaszonként lineáris függvénye a bemenetnek.
A gyakorlatban természetesen nem ennyire egyszerű függvényeket alkalmaznak, de nem is sokkal bonyolultabbakat, hanem nemes egyszerűséggel ilyenek kompozícióját. Tehát például egy két rétegű neurális háló két ilyen függvény kompozíciója, azaz az
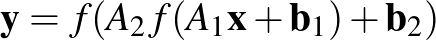
függvény, amelyben 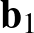 és
és 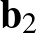 vektorok (nem feltétlenül azonos dimenziósak),
vektorok (nem feltétlenül azonos dimenziósak), 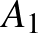 és
és 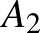 mátrixok (nem feltétlenül azonos méretűek),
mátrixok (nem feltétlenül azonos méretűek), 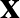 a bemenet, és
a bemenet, és 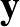 a kimenet. Amennyiben rétegekre bontjuk, akkor az első réteget az
a kimenet. Amennyiben rétegekre bontjuk, akkor az első réteget az 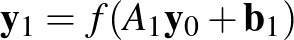 függvénykapcsolat reprezentálja, a második réteget pedig az
függvénykapcsolat reprezentálja, a második réteget pedig az 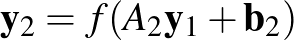 . A teljes háló ezután a kettő kompozíciója:
. A teljes háló ezután a kettő kompozíciója:

A deep-learning elnevezést takaró mélyhálókban sok réteg lehet, egy  rétegű háló a fenti képlet után már nagy meglepetést nem okoz:
rétegű háló a fenti képlet után már nagy meglepetést nem okoz:
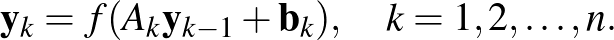
Ezen a ponton a téma bemutatását lezárjuk, bár a történet igazán most kezdődik. Cikkünk célja csupán az volt, hogy bemutassuk azokat a matematikai kereteket, amelyek a címben szerepelő fogalmak mögött vannak. Egy következő cikk szólhat arról, hogy mit jelent a neurális háló tanítása, milyen matematikai eszközöket fejlesztettek ki erre, és ami talán mindenkit a legjobban érdekel, mit képesek a neurális hálók „megtanulni”, illetve mik lehetnek a korlátaik.
Simon L. Péter,
ELTE TTK Alkalmazott Analízis és Számításmatematikai Tanszék