Egy könyv előszavát olvasva két (más-más okból) érdekes jelölésbe botlottam. A szerző megjegyzi, hogy a bizonyítások végét a Halmos-féle négyzettel, az odafigyelést igénylő bonyolult részeket pedig a margón elhelyezett Bourbaki-féle veszélyes kanyar szimbólummal jelöli. Ez adta az apropóját ennek a cikknek, erről a két jelölésről (nem igazán, vagy alig) lesz most szó.
Halmos és Bourbaki
A négyzet szimbólumot úgy hiszem sokan ismerik, de nem mindenki tudja, hogy a neve (amellett persze, hogy „négyzet”) Halmos. Sőt, néha csak halmos, kis h-val. Régi könyvekben a bizonyítások végét legtöbbször a Q.E.D., azaz a Quod Erat Demonstrandum jelezte, a mai könyvekben ezt a szerepet már szinte mindenhol átvette a halmos. De honnan a név?
Halmos Pálról néhány bekezdést írni sokkal nehezebb, mint néhány teljes cikket, mert az ember nem tudja eldönteni, hogy miről ne írjon. Én most megelégszem annyival, hogy az olvasó figyelmébe ajánlom az „I Want to Be a Mathematician: An Automathography” című könyvet, amelyben (a Wikipediát idézve) így ír a ▯-ről:
„The symbol is definitely not my invention — it appeared in popular magazines (not mathematical ones) before I adopted it, but, once again, I seem to have introduced it into mathematics. It is the symbol that sometimes looks like ▯, and is used to indicate an end, usually the end of a proof. It is most frequently called the 'tombstone', but at least one generous author referred to it as the 'halmos'." (A jelölést egyértelműen nem én találtam ki — népszerű magazinokban tűnt fel (nem matematikaiakban), mielőtt én adaptáltam volna, de, ismétlem, úgy tűnik, én vezettem be a matematikában. Ez az a szimbólum, ami időnként így néz ki: ▯, és a véget, legtöbbször egy bizonyítás végét jelzi. Leggyakrabban 'sírkő'-nek nevezik, de volt legalább egy nagylelkű szerző, aki 'halmos'-ként említette. A szerk. )
Halmosnak nemcsak a tudományos életműve rendkívül sokszínű, hanem ő maga is egy nagyon sokszínű és nagyon szórakoztató ember, többek között felbecsülhetetlen fénykép hagyatékot hagyott hátra. Legendás volt arról, ahogyan matematikát írt, és arról is, ahogy arról írt, hogy hogyan írjunk matematikát [4]. Ellenpontként álljon itt a szintén legendás Jean-Pierre Serre előadása arról, hogy hogyan írjunk matematikát rosszul. Azt hiszem ez az egyik legszellemesebb matematikával kapcsolatos videofelvétel, ami valaha készült.
Halmos Pál nevét őrzi a Paul R. Halmos – Lester R. Ford Award is, amelyet kiemelkedően megírt matematikai cikkekért ítélnek oda. A díjat az American Mathematical Society alapította 1964-ben, akkor még Lester R. Ford Award néven. Érdekességként megemlítem, hogy a díjat 2020-ban két magyar matematikusnak, Gerencsér Balázsnak és Harangi Viktornak ítélték oda a „Too Acute to Be True: The Story of Acute Sets” című írásukért. Egyébként a díj 1971-es díjazottjai közül kettő igazán érdekes a jelen írás szempontjából:
Paul R. Halmos, Finite-dimensional Hilbert spaces, The American Mathematical Monthly, Vol. 77, (1970), pp. 457–464.
Jean A. Dieudonné, The work of Nicolas Bourbaki, The American Mathematical Monthly, Vol. 77, (1970), pp. 134–145.
Ezzel rögtön rá is térhetünk a címben szereplő másik névre, Nicolas Bourbakira. Bourbakiról néhány bekezdést írni még nehezebb, mint Halmos Pálról. Nem csak azért, mert Bourbaki nevű matematikus nem létezik, hanem azért, mert a Bourbaki név egy generációkon átívelő, változó tagösszetételű csoportot jelöl. Közülük az egyik legprominensebb, épp a fent említett Jean A. Dieudonné.
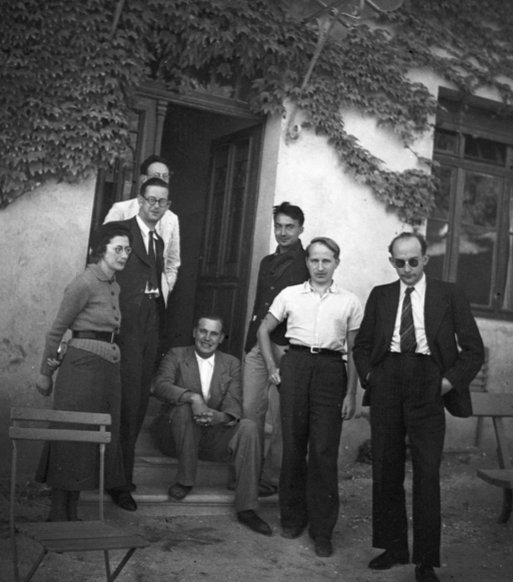
Fotó a Bourbaki-csoport 1938-as összejöveteléről: Simone Weil, Charles Pisot, André Weil, Jean Dieudonné, Claude Chabauty, Charles Ehresmann és Jean Delsarte.
A Bourbaki-csoport éppen aktuális névsora általában nem ismert, csak a tagság megszüntével derül ki egy-egy emberről, hogy tag volt. A fent említett Jean-Pierre Serre is egy közülük. Róluk nem egy-egy bekezdést, hanem egy-egy különálló cikket lehetne (sőt kéne) írni. A Bourbaki-csoport összejöveteleiről egyébként sokat meg lehet tudni Armand Borel visszaemlékezéseiből [1].
A Bourbaki-csoport legfőbb munkája az Éléments de Mathématique című könyvsorozat, amelynek célja a matematika nagyon szigorú (egyesek szerint túlságosan szigorú) megalapozása. Ebben használták a veszélyes kanyar szimbólumot azon szakaszok megjelölére, amelyeknél az olvasónak óvatosnak kell lenni, és figyelni kell egyes részletekre annak érdekében, hogy rajta maradjon a helyes úton.
Részlet az integrálelméletről szóló kötetből.
Lehet, hogy az olvasó a veszélyes kanyar szimbólummal most találkozott először. Az viszont biztos, hogy az üres halmazt jelölő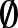 
szimbólumot szinte mindenki ismeri. Ez is egy Bourbaki jelölés, André Weil vette kölcsön a norvég abc-ből. Egyébként amellett, hogy a Bourbaki-csoport rendkívül rigorózus volt, ha könyvírásról volt szó, ami a nyelvezetet illeti, igyekeztek meglehetősen hétköznapi elnevezéseket bevezetni. Így például a zárt, konvex, kiegyensúlyozott, és elnyelő halmazokra bevezették a hordó (mint a bor tárolásához használt tárgy) elnevezést. Egyébként a legenda szerint a belső használatra fenntartott szókincsük a vártnál is gazdagabb volt. Így például a sesqui-lineáris forma helyett a könnyen megjegyezhető „szexilineáris formák”, a bornológikus helyett pedig a „bornográf” elnevezést használták. A Bourbaki-csoport történetére még egy mondat erejéig visszatérve: 1952-ben megalakult az „Association des Collaborateurs de Nicolas Bourbaki”, amely azóta is aktív. A híres Bourbaki szemináriumon rendszerint egy-egy friss és jelentős eredményt mutat be egy arra felkért matematikus. Ismét megemlítek egy magyar vonatkozást, Charles Bordenave 2018-ban Backhausz Ágnes és Szegedy Balázs eredményeit prezentálta. Az erre az alkalomra elkészített cikk és az előadás felvétele is elérhető az interneten.
Egy veszélyes kanyar
Visszatérek a bevezetőhöz. Amikor azt láttam, hogy a Halmosra és a Bourbaki-féle veszélyes kanyarra itt külön felhívják a figyelmet, megjegyeztem magamnak, hogy rendben van, de amúgy ezeket valószínűleg mindenki tudja. Aztán elkezdtem azon gondolkodni, hogy még ezeken kívül melyik jelölések eredetét ismerem, és legnagyobb meglepetésemre arra jutottam, hogy egyikét sem. (De akkor pont a Halmost és a veszelyes kanyart miért?) Eleinte olyanoknak próbáltam utánajárni, hogy ki vezette be a deriválásra használt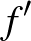 
-t, de aztán rájöttem, hogy nem kell ennyire előreszaladni, mert még azt sem tudom, hogy ki vezette be az összeadásra használt 
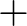jelet. Vagy mondjuk az egyenlőségjelet. Vagy szó szerint bármelyik másik jelet.
Ezután jött az igazán veszélyes kanyar. Azt tettem, amit manapság mindenki tesz, ha nem tud valamit: megkérdeztem a Chat GPT-t. Ahogy az ilyenkor lenni szokott, az internet nagyjából tíz perc alatt betemetett érdekességekkel. Néhány teljes munkanapot el lehetne vesztegetni ezekkel a dolgokkal. Természetes módon keletkezett a böngészőben egy rakás új fül, amiket majd egyszer mindenképp elolvasok, és amiket természetesen soha nem fogok elolvasni, hiszen néhány nap őrizgetés után véletlenül be fogom őket zárni, és azt is elfelejtem, hogy léteztek.
A 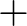-ról és az 
-ről írottakat a cikk kedvéért azért megnéztem. A 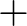jel első ismert előfordulása Johannes Widmann 1489-ben kiadott könyvében, a „Mercantile Arithmetic” vagy „Behende und hüpsche Rechenung auff allen Kauffmanschafft” [6] című munkában található. (Szabad fordításban „Gyors és tetszetős számítások mindenféle kereskedelemi ügylethez”.)
Ebben a könyvben 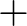a és a 
jeleket kereskedelmi kontextusban használták: a többletet és a hiányt jelölték velük. Az összeadás jelölésére azelőtt szavakat vagy rövidítéseket használtak. Például a latin et (és) szót vagy annak stilizált változatát. A Tiro-féle rövidírás rendszere, amelyet az ókori Rómában használtak, szintén előfutára lehetett a 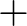jelnek.
Ami pedig az egyenlőségjelet illeti, az bevezetése előtt különféle szavakat, vagy rövidítéseket használtak, mint például: a latin aequatus, aequalis vagy ezek rövidítéseit, például aeq. Az szimbólumot egy Robert Recorde nevű walesi matematikus vezette be 
-ben a „The Whetstone of Witte” című munkájában.
Az egyenlőségjel első előfordulása.
A lényeget a régi angol nyelv ismerete nélkül is ki lehet érteni a szövegből: annak érdekében, hogy elkerülje az „egyenlő” szó unalmas ismételgetését, bevezeti a párhuzamos és egyenlő hosszú vonalakat (a Gemowe jelentése iker), mert noe .2. thynges, can be moare equalle, azaz nincs két dolog, ami azoknál egyenlőbb lehet.
Ahogyan korábban írtam, ilyen érdekességeket ma már pillanatok alatt meg lehet találni, és percek alatt le is lehet ellenőrizni, vagy el lehet felejteni. Ha a tisztelt olvasó úgy gondolja, hogy ismer olyan jelöléseket, amelyeknek a története érdekes (minden jelölés ilyen), van kedve és ideje írni róluk, akkor írjon, és küldje be az Érintőbe! (Ez az e-mail-cím a szpemrobotok elleni védelem alatt áll. Megtekintéséhez engedélyeznie kell a JavaScript használatát.)
Titkos Tamás,
Budapesti Corvinus Egyetem
és Rényi Alfréd Matematikai Intézet
Hivatkozások
- [1] Armand Borel, Twenty-five years with Nicolas Bourbaki, Notices Amer. Math. Soc. 45 (1998), 373–380.
[2] Gerencsér Balázs és Harangi Viktor, Too Acute to Be True: The Story of Acute Sets, The American Mathematical Monthly, Volume 126, Number 10, November 2019, pp. 905–914.
[3] Paul R. Halmos, I Want to be a Mathematician: An Automathography, Springer Science & Business Media, 2013.
[4] Paul R. Halmos, How to write mathematics, L’Enseignement Mathématique, Vol.16 (1970)
[5] Robert Recorde: The Whetstone of Witte (1557)
[6] Johannes Widmann, Behende und hübsche Rechnung auff allen kauffmanschaft, Leipzig: Konrad Kachelofen 1489.