Hogy volt?
Valamikor a 90-es évek végén hallottam először számítógépes bizonyításról, amikor a televízióban még gyakran voltak esti beszélgetős kulturális műsorok. A töretlen fejlődésben bízó korosztály tagjaként meglepve hallottam, hogy a számítógépes bizonyításokra a matematikusok egy része nagyfokú bizalmatlansággal tekint. Mérő László, aki az adás vendégeként beszélt erről, természetesen a négyszíntételt hozta példaként.
A négyszíntétel egy közismert matematikai állítás, amely szerint bármilyen síkban rajzolt térképen a területek (például országok, kerületek, megyék, grófságok, vármegyék, szolgabíróságok) úgy színezhetők ki négy színnel, hogy két szomszédos terület soha ne kapjon azonos színt. Ha a BME főépülete előtti járdaszakaszon sétálunk, könnyen észrevehetjük ennek az összefüggésnek a modern kori street art ábrázolását. A sejtést először 1852-ben Francis Guthrie fogalmazta meg, aki akkor még Londonban tanult, később viszont a dél-afrikai Fokvárosban lett matematikaprofesszor és a botanika kutatója. A sejtést több sikertelen bizonyítási kísérlet után 1976-ban Kenneth Appel és Wolfgang Haken tudták végérvényesen igazolni. Ha a négyszíntétel hamis lenne, akkor léteznie kellene legalább egy „térképnek”, amely a lehető legkisebb számú tartományból áll, de mégis öt színre van szükség a kiszínezéséhez. Appel és Haken bizonyítása az 1936 darab lehetséges minimális reduktum végigszámolásával kimutatta, hogy ilyen ellenpélda nincs. Ezzel a tétel lett az első jelentős matematikai eredmény, amelyhez nélkülözhetetlen volt a gépi számítás. Az Illinois-i egyetem két matematikusa IBM gépi kódú programot írt. Néhány közeli város IBM számítógépéhez volt hozzáférésük: az Urbana városi egyetemi kampusz IBM 360-75 mainframe gépéhez, majd a chicagoi IBM 370-158-ashoz, végül az egyetemi adminisztrációt végző IBM 370-168 adatfeldolgozó egység munkaidejét is használhatták. Azt hiszem, nem lepődik meg senki azon, hogy köszönetet mondtak az Illinois Állami Egyetem Számítógépes Szolgáltató Központja alkalmazottainak. Az adattároláshoz mintegy 2,5 MB összes tároló kapacitásra volt szükségük. Meglepően gyorsan futottak a programok, kb. 15–30 perc alatt végezték el a számításokat. Mindazonáltal a 370-es „nagy vasaknak” is csak 2 MB kapacitásuk volt, ezért kellett több gépen futtatni a programokat [1]. A 90-es években már sokaknak itthon is volt 120 MB-os személyi számítógépe, ami talán megmosolyogtatóvá teszi a történetet, de a technika fejlődése már csak ilyen.

A gépi bizonyítás sikere vitát indított el a matematikai közösségben. A fő kérdés: vajon teljes mértékben megbízhatunk-e egy olyan bizonyításban, amelyet nem tudunk teljes egészében az emberi percepcióra és a tiszta észre hagyatkozva ellenőrizni? A matematikus mindennapi gyakorlatához hagyományosan hozzátartozik az emberi értelem által átlátható és ellenőrizhető bizonyítások készítése és a bizonyítások manuális ellenőrzése. Az Appel–Haken-féle gépi bizonyítás azonban olyan méretű és nemhumán dokumentáltságú volt, hogy azt ember nem tudta volna követni, így felmerült a kérdés, mennyire elfogadható egy ilyen bizonyítás. Egyáltalán: mit tekintünk bizonyosságnak a matematikában? Ha egy géppel helyettesítjük az emberi gondolkodást, de mi nem tudjuk ellenőrizni a gép minden lépését, akkor vajon ugyanúgy bízhatunk-e az eredményben, mint amikor egy matematikus kolléga ellenőrzi a munkánkat?
Az egyik fő ellenvetés tehát a különböző szintű áttekinthetetlenség. Nos, 2005-ben Georges Gonthier kanadai matematikus, a Microsoft Research kutatója a francia INRIA kutatóintézet munkatársaival egy elvileg áttekinthetőbb módon, a Coq bizonyításasszisztenssel is igazolta a tételt [6]. A Coq, Agda és Lean típusú bizonyításasszisztensek működése bizonyos értelemben szembeállítható ezekkel a specializált megoldásokkal, amilyen a négyszínsejtés assembly bizonyítása is volt.1 Míg a kezdetleges típusrendszerű programnyelvek esetén csak esetellenőrzésekre számíthatunk és gyakran ezek is átláthatatlanok, addig a bizonyításasszisztensek fel vannak vértezve minden olyan nyelvi képességgel, amely a matematikai állítások és bizonyítások teljes leírására teszi őket alkalmassá, és a humán matematikai gondolkodás logikáját lépésről lépésre követve vezetik a felhasználót a gépi levezetés mentén. Az automatizációs lépéseik is intuitívak és a szokásos napi bizonyítási módszereken alapulnak, szemben a speciális programok működésével.
Bizonyításasszisztencia: az ember és a gép tánca
A fent említett programnyelvek a Martin-Löf-típuselméletre alapulnak, ami egy programozási nyelv és nagyon erős kapcsolatban áll az úgynevezett természetes levezetéssel. Ez utóbbi arról kapta a nevét, hogy csak olyan levezetési szabályok (és ezek lehetnek akár nem-logikaiak is) alapján működnek, amik nagyon jól modellezik a matematikusok által használt mindennapi következtetéseket. Az egyik komputációsan kitüntetett logikai rendszer az, amelyikben csak implikáció (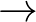 ) és konjunkció (
) és konjunkció (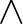 ) van, azaz rendre a „ha
) van, azaz rendre a „ha  , akkor
, akkor  ” és az „
” és az „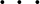 és
és 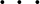 ". Ezt az (intuicionista) logika negatív fragmentumának nevezzük. Például, ha be szeretnénk bizonyítani az alábbiakat, akkor elég ez a logika.
". Ezt az (intuicionista) logika negatív fragmentumának nevezzük. Például, ha be szeretnénk bizonyítani az alábbiakat, akkor elég ez a logika.
Tudjuk, ha a kulcs a titkárnál volt (B), akkor megvan a tettes (C), feltéve, hogy az elnök szabadságra ment (A). Tehát, ha az elnök szabadságra ment és a kulcs a titkárnál volt, akkor megvan a tettes.
Formálisan
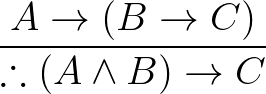
( 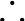 a „tehát” jele és Bertrand Russell használta először). Ez a szabály az egyik currying szabály (az un-currying, a konverze a currying) és nagyon fontos ebben a világban, mert azt mondja ki, hogy a konjunkció és az implikáció kategorikus-algebrailag barátságban vannak (az implikáció bal-adjungáltja a konjunkció).
a „tehát” jele és Bertrand Russell használta először). Ez a szabály az egyik currying szabály (az un-currying, a konverze a currying) és nagyon fontos ebben a világban, mert azt mondja ki, hogy a konjunkció és az implikáció kategorikus-algebrailag barátságban vannak (az implikáció bal-adjungáltja a konjunkció).
Az alapreláció az úgynevezett levezethetőségi reláció:
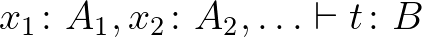
(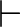 a „turnstyle”, azaz forgókapu, itt: „levezethető”). Ezt az módfelett összetett relációt a következőképpen olvassuk: amennyiben az
a „turnstyle”, azaz forgókapu, itt: „levezethető”). Ezt az módfelett összetett relációt a következőképpen olvassuk: amennyiben az 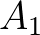 ,
, 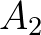 ,
, 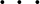 állításoknak van levezetésük, amelyeket rendre az
állításoknak van levezetésük, amelyeket rendre az 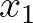 ,
, 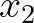 ,
, 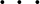 változókkal jelölünk, és ezekből valamint a levezetési szabályok alkalmazásával összeállítható a
változókkal jelölünk, és ezekből valamint a levezetési szabályok alkalmazásával összeállítható a 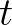 bizonyításkód, akkor ez a
bizonyításkód, akkor ez a 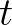 kód az
kód az 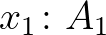 ,
, 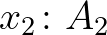 ,
, 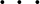 feltételrendszerben bizonyítja a
feltételrendszerben bizonyítja a 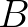 állítást. Melyek a levezetési lépések kódjai és mik a bizonyításokat legyártó szabályok? Nos, a szabályoknak most szándékosan úgy adunk nevet, hogy az megfeleljen a Lean programnyelv parancsainak. (A russelliánus
állítást. Melyek a levezetési lépések kódjai és mik a bizonyításokat legyártó szabályok? Nos, a szabályoknak most szándékosan úgy adunk nevet, hogy az megfeleljen a Lean programnyelv parancsainak. (A russelliánus 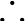 -t jelölését ezúttal már lehagyjuk.)
-t jelölését ezúttal már lehagyjuk.)
(exact) 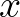 |
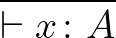 |
intro  |
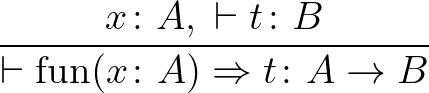 |
(apply)  |
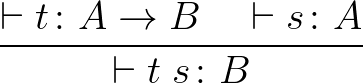 |
And.intro 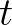 |
 |
 .left .left |
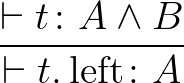 |
 .right .right |
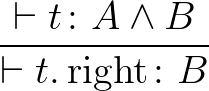 |
Levezetési szabályok
A Lean nyelven a tétel az alábbi (https://github.com/mozow01/TypeTheoryWorkshop/blob/main/Logic.lean):
theorem Curry (A B C: Prop) (x: A -> (B -> C)): A /\ B -> C := by
A „by” parancs megnyitja az úgy nevezett interaktív bizonyításmódot, amelyben elkezdünk beszélgetni a levezetési rendszerrel. Vár tőlünk egy ötletet, amely után hajlandó visszakérdezni. Van egy nagyon szellemes megfogalmazás arra, hogy egy bizonyítást hogyan folytatunk le. Ez pedig az, hogy ebben a világban bizonyítani nem más, mint időutazást végezni a múltba.2 Szeretnénk a végére járni, hogy miért lehet az, hogy a tétel igaz, ezért megpróbáljuk visszafelé feltárni, mi vezethetett ehhez a megállapításhoz. Néha azt érzékeljük, hogy nem azon az okozati ágon próbáljuk megközelíteni az elégséges alapot, amelyen vagyunk, ilyenkor picit előre kell utaznunk a múltból a jelen felé. Nos, most az ötlet az, hogy ha a végcél egy 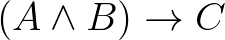 „függvény” alakú állítás, úgy csak egyetlen úton juthattunk el ide, azzal, hogy az intro szabályt használtuk. Keressük fel a táblázatban és győződjünk meg róla, hogy ez az egyetlen olyan szabály, ami ilyen alakú tételt ereményez. Magyarán tegyük fel, hogy van egy
„függvény” alakú állítás, úgy csak egyetlen úton juthattunk el ide, azzal, hogy az intro szabályt használtuk. Keressük fel a táblázatban és győződjünk meg róla, hogy ez az egyetlen olyan szabály, ami ilyen alakú tételt ereményez. Magyarán tegyük fel, hogy van egy 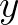 bizonyításunk arra, hogy
bizonyításunk arra, hogy 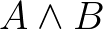 igaz. A Lean nyelven a tétel az alábbi (https://github.com/mozow01/TypeTheoryWorkshop/blob/main/Logic.lean):
igaz. A Lean nyelven a tétel az alábbi (https://github.com/mozow01/TypeTheoryWorkshop/blob/main/Logic.lean):
/- x: A -> B -> C |- A /\ B -> C -/ intro y /- x: A -> B -> C, y: A /\ B |- C -/
Most rátekintünk a változóinkra és megkíséreljük észrevenni, hogy mely következtetés vezet el végül ahhoz a tényhez, hogy 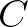 igaz. Ez az
igaz. Ez az 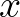 változó (vagy ha tetszik lemma), amelynek a típusa
változó (vagy ha tetszik lemma), amelynek a típusa 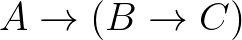 . Ezt alkalmazuk a
. Ezt alkalmazuk a 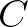 célra az apply
célra az apply 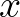 paranccsal. Ekkor a Lean visszakérdez: jó, és az
paranccsal. Ekkor a Lean visszakérdez: jó, és az 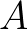 -ra és a
-ra és a 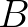 -re van bizonyításod? Így segít szókratészi kérdésekkel a Lean, így folyik a levezetés tánca a gép és az ember között. A válasz az, hogy igen, az
-re van bizonyításod? Így segít szókratészi kérdésekkel a Lean, így folyik a levezetés tánca a gép és az ember között. A válasz az, hogy igen, az 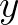 premisszából kell a konjunkció bal és jobb szabályával kinyerni
premisszából kell a konjunkció bal és jobb szabályával kinyerni 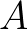 és
és 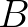 bizonyítását.
bizonyítását.
apply x; apply And.left y; apply And.right y /- case #1: x: A -> B -> C, y: A /\ B |- A case #2: x: A -> B -> C, y: A /\ B |- B -/ #print Curry /- theorem Curry: forall (A B C: Prop), (A -> B -> C) -> A /\ B -> C := fun A B C x y => x y.left y.right -/
Láthatóan meg is született a bizonyítás, a Lean interaktív ablakában a „No goals” üzenet jelent meg, azaz a Lean elfogadta a bizonyítást helyesnek. A levezetéskód, ha bárkit érdekel kiírható és ott virít a Curry név után.
Vegyük észre, hogy a bizonyítás lépéseinek leírása során semmilyen matematikán kívüli technikai dolgot nem kellett használnunk! Azt írtuk, amit egy humán, de kínosan részletes bizonyítás során is írnánk. Ha már bizonyítást írunk, miért írnánk azt kézzel? Írjuk MS Wordben! De ha már sokkal jobb képleteket tud szedni a LATEX, miért írnánk Wordben, írjuk LATEX-ben! 2024 kérdése a következő: ha a Lean nemcsak nyomdailag jól kiszedi, de matematikai helyesség szempontjából ellenőrzi is a munkánkat, miért ne írhatnánk a bizonyításainkat Leanben?3
Hogy véletlenül se gondoljuk, hogy itt pusztán „logikai programozásról” van szó, és csak a matematika és a logika céljait szolgálják ezek a programnyelvek, nézzünk egy példát, amely rámutat arra, hogy a fenti felépítés alkalmas nagyon általános keretrendszerben értelmezett informatikai adattípusokon végrehajtott eljárások implementálására is. Ez a jelenség annak köszönhető, hogy a fenti felépítésben a szabályok mindegyike bemenet-kimenet formájú, azaz fogad adatokat és visszaad egy adatot. Mi más lenne egy programozó vágya, mint egy ilyen logika? A példa az option típuskészítő operáció lesz. A Haskell kedvelők maybe monádként ismerhetik ezt a típust. Az option a kivételeket kezeli egyfajta módon. Elképzelhető, hogy vannak olyan eljárások, amelyek nem teljesen értelmezett függvényeket valósítanak meg, hanem bizonyos értékekre nem értelmezettek. Ezen algoritmusok kezelésére kiváló egy olyan konstrukció, amely becsomagolja a kimenő adatokat. Ha van kimenő adat, mondjuk 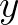 , akkor a some
, akkor a some 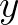 értéket adja vissza a csomagolás, ha nincs, akkor a none értéket. Lássuk ennek a levezetési szabályait!
értéket adja vissza a csomagolás, ha nincs, akkor a none értéket. Lássuk ennek a levezetési szabályait!
| none | 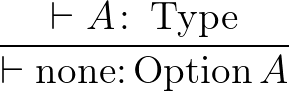 |
| some | 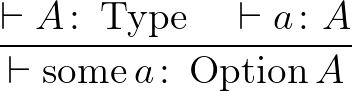 |
| Option.elim | 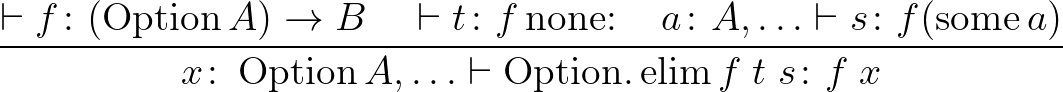 |
Option levezetési szabályok
Az első két szabály azt mondja, hogy mik építik fel ezt a típust: a none (nincs adat) érték és a some értékek. A harmadik szabály szerint, egy 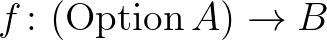 függvény megadásához elegendő megadni, hogy a none-on mit vesz fel és hogy a some-okon mit vesz fel, ez teljesen leírja
függvény megadásához elegendő megadni, hogy a none-on mit vesz fel és hogy a some-okon mit vesz fel, ez teljesen leírja  értékeit. Ezekkel a szabályokkal például meg lehet adni egy alábbi függvényt:
értékeit. Ezekkel a szabályokkal például meg lehet adni egy alábbi függvényt:
def Opt (A B: Type): Option (A -> B) -> (Option A -> Option B),
csak a fenti szabályokat kell alkalmazni. A Coq, Agda és Lean típuselmélete olyan erős kifejezőképességű, hogy a matematika teljes leírása elfér benne sőt, a programozásnak a számítógép fizikai megvalósításától független része is.
Mennyire hatékony egy ilyen bizonyító rendszer?
Rendkívül lelkesítő lehet a mesterséges intelligencia és a gépi megoldások kedvelőinek a tény, hogy a szuperszámítógépeken futó sakkprogramok képesek legyőzni a sakknagymestereket. Mindazonáltal látni kell, hogy a matematikai tételek bizonyíthatóságának eldöntése nem abba a bonyolultsági osztályba tartozik, amelybe a sakk. Jól jellemzi a sakk bonyolultságát, ha elrugaszkodunk a  -as táblától és az
-as táblától és az 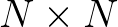 -es esetet tekintjük, hiszen ez árulkodik arról, hogy mekkora méretű ugrás jelentkezik a műveletigényben, ha a vizsgált terület mérete növekszik. Nos, az általánosított sakk számítási bonyolultsága exponenciális idejű és ebben a nemében teljes (EXPTIME-teljes), ami durván azt jelenti, hogy az ember számára ez a számítási bonyolultság megközelíthetetlenül nagy. Persze ez nem azt jelenti, hogy a
-es esetet tekintjük, hiszen ez árulkodik arról, hogy mekkora méretű ugrás jelentkezik a műveletigényben, ha a vizsgált terület mérete növekszik. Nos, az általánosított sakk számítási bonyolultsága exponenciális idejű és ebben a nemében teljes (EXPTIME-teljes), ami durván azt jelenti, hogy az ember számára ez a számítási bonyolultság megközelíthetetlenül nagy. Persze ez nem azt jelenti, hogy a 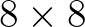 -as sakkjátékot ember ne tudná játszani, de valahogy mérni kell a komputációs nehézséget. Az is jól látható ezen a bonyolultsági jellemzésen, hogy a sakk egy kétszereplős játszma. Így is tanul a sakkjátékgép: saját magával játszik sokat.
-as sakkjátékot ember ne tudná játszani, de valahogy mérni kell a komputációs nehézséget. Az is jól látható ezen a bonyolultsági jellemzésen, hogy a sakk egy kétszereplős játszma. Így is tanul a sakkjátékgép: saját magával játszik sokat.
A bizonyíthatóság kiderítése nem ilyen probléma. A tartalmasabb esetekben mégcsak nem is eldönthető, azaz nincs olyan algoritmus, amely véges lépésben el tudná dönteni, hogy egy matematikai tétel bizonyítható vagy nem bizonyítható. Ezek félig eldönthető problémák, azaz van hozzájuk olyan eljárás, amely véges lépésben megtalálja egy tétel bizonyítását, ha van, de nem feltétlenül jár sikerrel véges lépésben, ha az az eset, hogy az adott tétel nem bizonyítható. Ebből a szempontból a bizonyításkereső szoftvereknek nehezebb dolguk van, mint a sakkprogramoknak. Van egy jó tulajdonsága azonban a bizonyításasszisztenseknek, hogy gyorsan ellenőrizni tudják, hogy az adott bizonyítás helyes-e, azaz a bizonyítás hosszának növekedésével csak hatványfüggvény méretben nő az ellenőrzés műveletigénye. Ezeknek a programoknak a működése tehát úgy zajlik, hogy automatikus bizonyításkereső szubrutinok vagy emberi tippek javaslatot adnak az igazolásra, amit aztán lépésenként ellenőriz a program és interaktív módon kérdésekként, bizonyítási célokként adja vissza azokat a lemmákat, amelyeket igazolni kéne a siker eléréséhez.
Az asszisztensek és a tételbizonyítók persze nagyon nem ugyanolyan szoftverek. A tételbizonyítók (automated theorem provers, ATP) jellemzően erős és az ember által részleteiben nem feltétlenül áttekinthető keresési algoritmusokkal dolgoznak. Ennek egyik ismert fajtája az elsőrendű rezolúció, ami persze szintén csak félig-eldöntő módszer és mivel olyan bizonyítást ad, ha ad, ami a reductio ad absurdumot (az ellentmondásra visszavezetést) használja, ezért részben emiatt is nehezen olvasható. A tételbizonyítók hatékonysága sokszor azon múlik, hogy nagyon speciális környezetben dolgoznak. Az egyik ilyen például az AlphaGeometry szimbolikus motorja, amely erősen korlátozott kifejezőképességű, és elemi síkgeometriai problémák megoldásával vívta ki figyelmet, továbbá azzal, hogy a heurisztikus része mesterséges intelligenciát használ [4]. Egy másik a Prover9/Mace4 páros, amelyik véges csoportelméleti problémák megoldásában jeleskedik. A Prover9 bizonyítást keres, a Mace4 ellenpélda után kutat, és véges modelleket épít, amelyek egy előre megadott elsőrendű formula által leírt tulajdonságnak felelnek meg. Ehhez a világhoz kötődik a GAP kompjuter algebra rendszer, amelyet szintén csoportelméleti problémák tárgyalására használnak. Nagy P. Gábor (Szegedi Egyetem, BME) nevezetes eredménye például az első nem-Moufang, véges egyszerű Bol-loop megkonstruálása, amivel megoldotta a loopelmélet akkoriban legjelentősebb nyitott problémáját [3]. A GAP szoftver fejlesztői között kell megemlítenünk sajnálatos módon nemrég elhunyt kollégánkat, a BME Algebra és Geometria Tanszék oktató-kutatóját, Horváth Erzsébetet, aki hosszú évekig dolgozott együtt az aacheni központú csoporttal.4
Nyilván a bizonyításkeresésbe beszállhat a mesterséges intelligencia is. A legújabb eredmény, hogy a matematikai diákolimpiák elemi síkgeometriai feladataira korlátozva a tárgyalás körét, a megoldásokon feltanítva egy mesterséges intelligenciát, elég jól tudtak bizonyítást keresni kutatók [4]. Hasonló problémán dolgoznak Szegedy Krisztián és kollégái. Az AI alkalmazásának sikeréhez mindenképpen két dolog kell: egyfelől elég szűkre kell venni a tárgyalás körét (pl. elemi síkgeometria), másfelől bizonyításasszisztenst (pl. HOL4/Isabelle-t) kell alkalmazni a megtalált (hallucinált) lehetséges bizonyítások ellenőrzésére [2].
Mennyire intelligens egy ilyen bizonyító rendszer?
Sem ember, sem gép nem tudja áthágni a Gödel-tételkör negatív eredményeit, azaz feltéve, hogy az aritmetika ellentmondásmentes, nincs olyan általános eljárás, amely eldönti, hogy egy számelméleti állítás igaz vagy sem. Ezért felvetődik a kérdés, hogy mi a viszonya a mesterséges és a természetes intelligenciának a matematikai igazságkeresés területén. Azt vizsgáljuk, hogy mennyire érti a gép, amit bizonyít; ezért vizsgálódásunkat az aritmetikára korlátozzuk. Ha a gép képes bizonyítani egy számelméleti tételt, vajon érti-e, amit bizonyít? Nyilvánvalóan gyorsabban csinálja, mint mi, de akkor ebben a gyengébb értelemben a gépi bizonyítás „felemelkedhet”-e az emberi bizonyítás fölé? Az én álláspontom az, hogy a gépi bizonyítás olyan mértékben az emberi gondolkodás tükörképe, hogy egy bizonyító gép annyira és csak annyira intelligens, mint mi magunk.
Az előbbi állítás két részből áll. Az első tézis szerint a gép nem értheti jobban a számelméletet, mint mi magunk. Ennek alátámasztására elegendő elővennünk a kínai szoba érvet. Mint közismert, John Searle amerikai analitikus filozófus egy nagyon éles érvet hozott fel annak alátámasztására, hogy a tiszta számítógépes programok nem érthetik jobban azt, amiről beszélnek, mint mi.5 A gondolatkísérlet a következő: képzeljük el, hogy van egy szoba, amelyben egy nagyon részletes szabálykönyv rögzíti az összes olyan társalgási szabályt, amely szükséges a kínai nyelven való kommunikációhoz. Ezt úgy kell elképzelni, hogy egy kis ablakon keresztül a szobába kérdéseket lehet bejuttatni kínai nyelven, és a benne ülő, kínaiul nem tudó ember úgy válaszol, hogy egyszerűen kikeres egy a kérdésre adható kínai választ és azt küldi vissza a kérdezőnek. Tegyük fel, hogy a kínai szoba átmegy a Turing-teszten, azaz nem derül ki, hogy aki a szobában ül nem érti, amit a kérdező mond. Nos, ebben az esetben a szobában tevékenykedő ember nem csinál mást, mint amit egy számítógép tesz, amely szabályok követésével válaszol kérdésekre. Ilyet látunk is: az OpenAI ChatGPT-je például így működik. Márpedig világos, hogy aki a szobában ül, nem tud kínaiul, ezért egy szót sem ért abból, amiről a beszélgetés zajlik, csak jeleket fogad, mechanikusan feldolgozza őket, és visszaad egy választ. A kínai szoba gondolatkísérlet tehát azt igazolja, hogy egy gép sem értheti, mire megy ki a játék, ha az az ember, aki a szobában ül, nem érti azt. A gép nem értheti jobban az aritmetikát, mint mi.
A második tézis, a fordított irány a meglepőbb. Az ember nem értheti jobban az aritmetikát, mint egy bizonyító gép. Már Stephen Kleene is felhívta a figyelmet arra, hogy a Turing-gép fogalma úgy van kialakítva, hogy a gép pontosan azokat a mechanizálható gondolati műveleteket tudja elvégezni, mint az emberi agy. Egy bizonyításasszisztens pontosan azokat az érvelési szabályokat alkalmazza, amelyeket az ember, ezért ha egy ember arra a következtetésre jut, hogy egy aritmetikai állítás igaz, akkor a bizonyító program is képes ezt ellenőrizni. Ennek az állításnak hallatán sokak hátán felállhat a szőr: tényleg nem okosabb az ember egy gépnél? És mi van az intuícióval? Nos, az intuíció sokszor megcsalja az emberi érvelőt. Ha nem ugyanazt tudná a gép számelméletből, amit az ember, akkor az pontosan azt jelentené, hogy vannak olyan számelméleti állítások, amelyeket az ember, mondjuk a rá jellemző mágikus vagy egyedi képességekkel igazként ismer fel, míg a gép nem tudja ezeket igazolni. Egy ilyen tényállással az lenne a gond, hogy ha a géppel lehetetlen lenne verifikálni, miért igaz egy ilyen tétel, akkor egy másik embernek sem lehetne sehogyan se elmagyarázni, hogy az miért igaz. Jóllehet egy másik ember, szintén eljuthatna valamiféle szubjektív, mágikus bizonyosságig a tétel igazságát illetően, de azért az mégsem menne át egy szigorú, hézagokat el nem viselő matematikai ellenőrzésen. Ember és gép egyaránt képes lehet „beflesselni”, hogy egy állítás igaz, de a végső mérleg, hogy megvan-e az állítás korrekt, objektív és egzakt bizonyítása. Szomorúan hangzik, de ezek az érvek azt igazolják, hogy egy ember pont ugyanannyit ért a matekból, mint egy – Turing szavait használva – gondolkodó gép.

Érdekességként jegyzem meg, hogy egyáltalán nem állítja Searle, hogy egy adott gép nem lehet intelligensebb egy embernél. Ami nem tud intelligensebb lenni, az egy pusztán szintaktikai műveleteket végző szoftver. A Star Wars univerzum robotjai például személyiséggel bírnak. Ha egy egyedi vaskasztni képes olyan tapasztalatra és személyiségre szert tenni, mint mondjuk R2-D2, akkor az akár képes lehet átvenni a hatalmat a világ felett.
A bizonyításasszisztensek mint a matematika kutatásszociológiájának megváltoztatói
A bizonyításasszisztens szoftverek jelentős előnyöket nyújtanak a matematikai tételek bizonyítása során, különösen a hibák és hézagok azonosításában. Ezek az eszközök képesek automatikusan észlelni a bizonyításokban rejlő logikai vagy formális hiányosságokat, ezáltal minimalizálva a rossz bizonyítások előállításának kockázatát.
A bizonyításasszisztens szoftverek használata a tudományos folyóiratok bírálói oldalán jelentősen felgyorsítják a bizonyítások ellenőrzésének folyamatát. A forráskódok egyszerű fordíthatósága révén a bizonyítások szintaktikai helyességellenőrzése embermentesen végrehajtható, ami lehetővé teszi, hogy a kutatók és a folyóiratok szakembereinek csak a szemantikai ellenőrzéssel kelljen foglalkozniuk. A formális bizonyítások megírása gyakran hosszadalmas, akár évekig is eltarthat a folyamat. Mégis a bizonyítások ellenőrzése seperc alatt zajlik, amely hozzájárul a tudományos igazságkeresés hatékonyságának vagyis a bizonyítások megbízhatóságának növeléséhez.
A bizonyításasszisztens szoftverek új lehetőségeket nyitnak a matematikai kutatás terén abban az értelemben is, hogy nem kellenek feltétlenül összeszokott, személyes és szakmai bizalomra alapuló csapatok a tételek igazolásához. Amennyiben egy kitűzött sejtést egy ilyen eszközzel bárki bebizonyít, a bizonyítás a gépi ellenőrzés révén automatikusan érvényesnek tekinthető. Nem véletlen, hogy az ilyen szoftverek matematikai alkalmazásakor hallgatók, akár már nagyon korán, az első szemeszterektől kezdve nagyon jól együtt tudnak dolgozni vezető kutatókkal. Ez a módszer a matematikai eredmények létrehozásában alacsonyabb belépési küszöböt igényelnek, szélesebb körből kerülhet ki egy jó bizonyítás, miközben az objektivitás és a megbízhatóság szintje nemhogy megmarad, de még növekszik is. Nem véletlen, hogy főleg hallgatók munkájának köszönhető, hogy az Imperial College-ban sikerült a Lean prover Mathlib nevű könyvtárában felhalmozni a BSc-s matematikus tananyagnak szinte az egészét. Tehát míg a Coq provert a programozási iparban (a formális verifikációban), az Agdát a magas szintű típusrendszerrel rendelkező programnyelvek tervezésben (az elméleti szoftvertudomány megalapozásában), addig a Lean-t a matematikai tételek bizonyításában lehet nagyon hatékonyan használni. Ennek két kiváló példája egyfelől Terence Tao, másfelől Randall Holmes egy-egy legutóbb Lean-ben bizonyított tétele.6 Tao két hallgatóval nemcsak bizonyította, de formálisan verifikálta is a polinomiális Freiman–Ruzsa-sejtést. Randall Holmes pedig egy nagyon érdekes, 60 éve magára várató logikai konzisztenciabizonyítást adott közre Lean-ben, amelynek a humán verziója 10 éve azért parkolt a folyóiratnál, mert nem volt olyan bíráló, aki képes lett volna végigolvasni a sok technikai részlet miatt.
A jövő útja, úgy tűnik, nem pusztán a mesterséges intelligencia, így a gép tételgeneráló képessége, hanem egy hibrid folyamat, amelyben a kutató a gép gyorsaságát és hibamentességét ötvözheti az emberi léptékű magyarázó erő és a humán kreativitás és intuitivitás képességével.
Molnár Zoltán Gábor
BME TTK Algebra és Geometria Tanszék
Irodalomjegyzék
- [1] Kenneth Appel and Wolfgang Haken and Jürgen Koch: Every planar map is four colorable. Part II: Reducibility Illinois Journal of Mathematics 21 (1977), 491–567. https://projecteuclid.org/journals/illinois-journal-of-mathematics/volume-21/issue-3/Every-planar-map-is-four-colorable-Part-II-Reducibility/10.1215/ijm/1256049012.full?tab=ArticleLinkCited
[2] Maciej Mikuła and Szymon Antoniak and Szymon Tworkowski and Albert Qiaochu Jiang and Jinyi Zhou and Christian Szegedy and Łukasz Kuciński and Piotr Miłoś and Yuhuai Wu: Magnushammer: A Transformer-based Approach to Premise Selection, arXiv:2303.04488 (2023) https://api.semanticscholar.org/CorpusID:257404922
[3] Gábor Péter Nagy: A class of finite simple Bol loops of exponent 2, Transactions of the American Mathematical Society, 361 (2007), 5331–5343 https://api.semanticscholar.org/CorpusID:15228937
[4] Trieu H. Trinh and Yuhuai Wu and Quoc V. Le and He He and Thang Luong: Solving olympiad geometry without human demonstrations, Nature, 625 (2024), 476–482 https://api.semanticscholar.org/CorpusID:267032902
[5] The mathlib Community: The Lean Mathematical Library, Association for Computing Machinery, New York, NY, USA, 2020, https://doi.org/10.1145/3372885.3373824, In: Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, New Orleans, LA, USA,
[6] Georges Gonthier (Ed. Deepak Kapur): The Four Colour Theorem: Engineering of a Formal Proof, In: Computer Mathematics, 8th Asian Symposium, ASCM 2007, Singapore, December 15–17, 2007. Revised and Invited Papers, Lecture Notes in Computer Science, 5081, 333, Springer, 2007, https://doi.org/10.1007/978-3-540-87827-8_28
[7] Georges Gonthier (Ed. Roberto Giacobazzi and Radhia Cousot): Engineering mathematics: the odd order theorem proof, The 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL '13, Rome, Italy - January 23–25, 2013, 1–2, ACM, 2013, https://doi.org/10.1145/2429069.2429071.
Lábjegyzetek
- 1 A három asszisztens oldalai rendre. Coq: https://coq.inria.fr/, Agda: https://wiki.portal.chalmers.se/agda/Main/HomePage, Lean: https://lean-lang.org/.
- 2 Az intuicionista logikai bizonyítás mint időutazás elnevezést Kaposi Ambrustól az ELTE Programozási Nyelvek Tanszékének docensétől hallottam.
- 3 Ezt az erősen lelkesítő gondolatmenetet Kevin Buzzardtól ismerjük, aki a londoni Imperial College-ban éllovasa a proof assistanteknek. Kollégáival és főleg hallgatóival képesek voltak a teljes BSc-s matematikus anyagot leprogramozni Lean4-ben és Mathlib4 néven elérhetővé tenni.
- 4 https://www.gap-system.org/Contacts/People/authors.html.
- 5 John Searle kiváló 2016-os előadása a Google Research-nél: https://youtu.be/rHKwIYsPXLg.
- 6 Terry Tao blogbejegyzése: https://terrytao.wordpress.com/2023/11/18/formalizing-the-proof-of-pfr-in-lean4-using-blueprint-a-short-tour/, Peter Smith blogbejegyzése: https://www.logicmatters.net/2024/04/21/nf-really-is-consistent/.











