Nagy egyszínű klikkek nyomában – áttörések a Ramsey-elméletben

1.  A hőskor: Ramsey, Erdős, Szekeres

Frank Plumpton Ramsey 1903-ban született Cambridge-ben, prominens értelmiségi családban. Apja, maga is matematikus, a Magdalene College rektora volt, bátyja pedig a későbbi Canterbury érsek. A Trinity College-ban évfolyama legjobbjaként doktorált matematikából, de korának minden nagy intellektuális kérdése érdekelte.

Frank Plumpton Ramsey

Maradandót alkotott a filozófiában, a gazdaságelméletben, a logikában és a statisztikában. Nem volt még 27 éves, amikor meghalt. Nagy hatással volt Wittgenstein filozófiájára, megtakarítással kapcsolatos munkáját Keynes „a matematikai gazdaságtan egyik legkiemelkedőbb teljesítményeként” értékelte. „Igazság és valószínűség” című munkája csaknem 20 évvel később Neumann és Morgenstern játékelméletében teljesedett ki.

Az ipari forradalom a XIX. században a matematikai módszerekre épülő műszaki- és természettudományok diadalát hozta. Közben sorra születtek a nagy eredmények a matematika szakterületein, az algebrában (Galois, Dedekind, Hilbert), az analízisben (Cauchy, Hadamard, Weierstrass), a számelméletben (Dirichlet, Gauss, Minkowski) és a geometriában (Bolyai, Gauss, Lobacsevszkij, Riemann). Egyre égetőbbé vált annak a filozófiával határos kérdésnek a megválaszolása, hogy hol húzódnak matematikai ismereteink határai. David Hilbert a matematikai világkongresszuson 1900-ban elmondott beszédében amellett érvelt, hogy a matematikában nincs „ignorabimus” (megoldhatatlan kérdés). „Tudnunk kell. Tudni fogjuk!” Gottlob Frege, Bertrand Russell és Alfred Whitehead hosszú kötetekben tettek kísérletet a matematikai tudományok precíz logikai megalapozására. Az egyik legnagyobb kihívás, az ún. „eldöntési probléma” (Entscheidungsproblem) volt, amelyet eleinte többen pusztán egy nehéz technikai kérdésnek tekintettek. Létezik-e olyan algoritmus, amely bármely megfelelő precizitással és jelölésrendszerrel megfogalmazott állításról eldönti, hogy igaz-e?

Egy ilyen alapvető tudományos kérdés nem hagyhatta hidegen a legkiválóbb diákokból álló „titkos” társaság, a „Cambridge-i Apostolok” egyik tagját sem, különösen pedig a matematikusokat. Ramsey egyetlen technikai jellegű matematikai cikkében, amelynek címe „On a problem of formal logic” (Egy formális logikai problémáról), pozitív választ adott az eldöntési problémára egy roppant speciális esetben, ún. univerzális elsőrendű logikai állításokra. Azt remélte, hogy további erőfeszítéssel módszere kiterjeszthető lesz minden állításra. Nem sokkal halála után – a matematikusok többségének megrökönyödésére és szomorúságára – Alonzo Church és Alan Turing bebizonyították, hogy nem ez a helyzet. Az állítások igazságának eldöntésére nincs algoritmus! A matematikai logika, a modellelmélet, a halmazelmélet és a filozófia máig birkózik a következmények feldolgozásával.

Az élet különös fricskája, hogy Ramseynek éppen az a munkája vált a leghíresebbé, amelynek eleinte alig tulajdonított jelentőséget. Fent említett cikkében ugyanis szerepelt egy egyszerűen megfogalmazható, teljesen újszerű matematikai tétel, amely önálló életre kelt, és mintegy fél évszázaddal később egy virágzó tudománnyá terebélyesedett. Ezt a területet ma Ramsey-elméletnek nevezünk. Ahhoz, hogy legegyszerűbb formájában kimondjuk az állítást, szükségünk van néhány definícióra.

Vegyünk egy -csúcsú teljes gráfot, 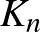-et, vagyis elemet (pontot, csúcsot), amelyek közül bármely kettőt él köt össze. Ezen él mindegyikét színezzük ki pirosra vagy kékre. Ha a pontok között találunk darabot úgy hogy bármely köztük futó él piros, akkor ezek egy piros klikket (vagy piros teljes részgráfot) alkotnak. Hasonlóan definiáljuk a -méretű kék klikkeket is.

1.1. tétel. (Ramsey [11]) Minden 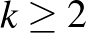egész számhoz található egy 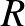egész szám, amire igaz, hogy akárhogyan színezzük meg egy 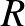-csúcsú teljes gráf éleit pirossal és kékkel, mindig találunk egy legalább -méretű egyszínű klikket.

A legkisebb olyan számot, amelyre az állítás igaz, 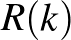-val jelöljük.

Világos, hogy 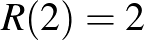. A 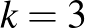esetet gyakran tárgyalják iskolai matematika szakkörökön. Bizonyítsuk be, hogy minden 6-tagú társaságban, amelynek bármely két tagja vagy szereti, vagy nem szereti egymást, mindig vannak 3-an, akik kölcsönösen szeretik egymást, vagy 3-an, akik kölcsönösen nem szeretik egymást! Feleltessünk meg a társaság minden tagjának egy pontot. Két pontot kössünk össze piros éllel, ha a megfelelő személyek szeretik egymást, és kékkel, ha nem. Az alábbi ábra mutatja, hogy az állítás nem igaz 5-pontú társaságok esetén, vagyis .

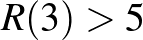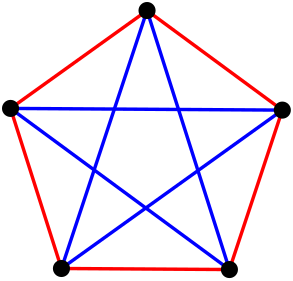
A feladat tehát annak igazolása, hogy 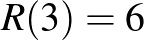, amit némi gondolkodás után bárki ellenőrizhet. Azt jóval nehezebb bebizonyítani, hogy 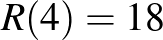. A következő Ramsey-szám, 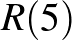értéke pedig már nem is ismert. Erdős Pál, aki – mint látni fogjuk – úttörő szerepet játszott a Ramsey-elméletben, a következőképp szerette tréfásan érzékeltetni a kérdés nehézségét. Képzeljük el, hogy egy gonosz és nagyhatalmú űrlény azzal fenyegeti az emberiséget, hogy mindenkit kiirt, ha nem mondjuk meg neki 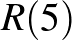értékét. Ebben az esetben a legjobb, amit tehetünk, ha összeszedjük matematikusainkat, összehangoljuk számítógépeinket, és megpróbáljuk kiszámítani a kért értéket. De mi van, ha a gonosz lény 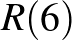értékét akarja? Akkor Erdős azt tanácsolja, hogy készüljünk háborúra, és próbáljuk megölni az ellenséget mielőtt elpusztít minket. Ez esetben ugyanis a számítógépek aligha segíthetnek. Végül Erdős szerette hozzátenni, hogy ha a matematikusok egyszer olyan okosak lesznek, hogy a kérdés megválaszolásához nem lesz szükségük számítógépre, akkor bátran mondhatjuk a gonosz lénynek, hogy eredjen a pokolba!

Ramsey-t kevéssé foglalkoztatta 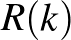pontos értéke, mert a kérdést motiváló algoritmikus feladat szempontjából ennek semmi jelentősége nem volt. Ramsey tétele egy időre feledésbe merült. Néhány évvel később egy geometriai probléma kapcsán azonban Erdős Pál és Szekeres György újra felfedezte a tételt, sőt később az is kiderült, hogy az jól használható a kombinatorikában és a matematika más területein is. Észrevették, hogy 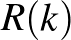becslését egyszerűsíti egy újabb paraméter bevezetése.

Erdős Pál és Szekeres György

Definíció: Legyen és 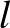két 1-nél nagyobb egész. Jelöljük 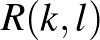-lel azt a legkisebb egész számot, amire igaz, hogy akárhogy színezzük meg egy -csúcsú teljes gráf éleit pirossal és kékkel, mindig találunk egy legalább -méretű piros klikket, vagy egy legalább 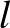-méretű kék klikket.

A fenti jelölésekkel nyilván 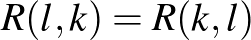és . Erdős és Szekeres nem csak azt bizonyították – újra és másképp –, hogy az 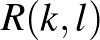érték létezik, hanem adtak is rá egy felső becslést, mégpedig egy binomiális együttható alakjában.

1.2. tétel. (Erdős–Szekeres [6]) Tetszőleges , 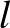pozitív egész számokra

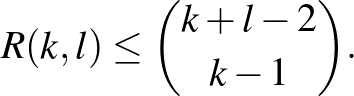
Innen azonnal következik, hogy 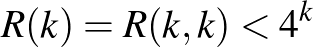és maga a pontos becslés is csak alig (-ban polinomiális faktorral) kisebb ennél. Később Erdős exponenciális alsó korlátot is talált az 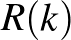Ramsey-számokra, mégpedig az általa felfedezett valószínűségi módszer egyik első alkalmazásával.

1.3. tétel. (Erdős [4]) Minden -nél nagyobb egész számra

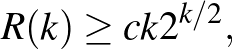
ahol egy -tól független konstans.

Az számokra vonatkozó legjobb explicit – tehát algoritmusokat és véletlen módszereket nem használó – konstrukciót Frankl Péter és Richard Wilson találta csaknem 45 évvel ezelőtt [13]. Ezeknek a gráfoknak a mérete 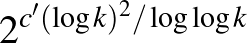, ahol 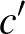egy pozitív konstans. Ez ugyan kisebb, mint a tételben szereplő korlát, de jóval nagyobb, mint 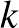bármely hatványa.

Az 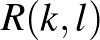Ramsey-számok definíciójában egy teljes gráf éleit színeztük pirosra és kékre. Sokszor természetesebb egy ezzel ekvivalens másik megfogalmazás, ahol csak a piros élek által alkotott gráfot vizsgáljuk. Ezek persze meghatározzák a kék éleket, amelyek a piros gráf ún. komplementer gráfját alkotják. A komplementer gráfban egy teljes részgráf (vagyis klikk) olyan csúcsokból áll, amelyek között az eredeti gráfban egyetlen él sem fut. Az ilyen csúcshalmazt független halmaznak nevezzük. Ebben a megfogalmazásban tehát 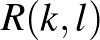az a legkisebb szám, hogy minden -csúcsú gráfban van egy -méretű klikk vagy egy 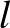-méretű független halmaz.

2.  Az „új hullám”

Az 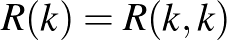számokat diagonális Ramsey-számoknak nevezzük, hiszen ha 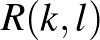értékeit egy táblázatba írjuk, ezek az értékek lesznek a főátlóban. A diagonális Ramsey-számokra az előző részben ismertetett felső becslés (eltekintve azoktól az esetektől, amikor nagyon kicsi) körülbelül az alsó becslés negyedik hatványa. Az ezek közötti nagy eltérés sok kutatót inspirált, de hosszú ideig egyik becslést sem sikerült érdemben (azaz nem csak egy -ban polinomiális faktorral) javítani.

Marcelo Campos, Simon Griffiths, Robert Morris és Julian Sahasrabudhe

Egészen tavalyig, amikor tehetséges fiatal kutatók egy új hulláma vetette rá magát a feladatra. 2023-ban Marcelo Campos, Simon Griffiths, Robert Morris és Julian Sahasrabudhe megjavította az 1.2. tételben adott felső becslést. Ez az első és leglényegesebb friss áttörés a Ramsey-elméletben.

2.1. tétel. (Campos, Griffiths, Morris és Sahasrabudhe [3]) Létezik egy olyan 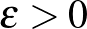konstans, hogy bármely 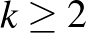egész számra .

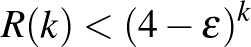Erdős 1.3. tételben idézett alsó becslésére azóta sem ismert hasonló javítás.

A matematikusok persze nem csak a diagonális Ramsey-számok nagyságrendjének becslésére fordítottak kiemelt figyelmet. A táblázat többi értéke is érdekes. Rögzítsük -t, és vizsgáljuk 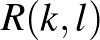nagyságrendjét, ahogy 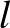végtelenhez tart. Más szóval – az 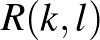függvény az első rész végén bevezetett alternatív definícióját használva – most arra vagyunk kíváncsiak, hogy mekkora gráfokra teljesül, hogy biztosan van bennük egy kis ( konstans-méretű) klikk vagy egy nagy független halmaz. Ismét másképp fogalmazva: legalább mekkora független halmaz létét tudjuk garantálni egy -csúcsú „-klikk-mentes” gráfban, vagyis egy olyanban, ami nem tartalmaz -méretű klikket.

A 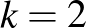eset triviális, hiszen a 2-méretű klikk egy él. Ha a gráfnak nincs éle, akkor az összes csúcs egy független halmazt alkot, amiből látszik, hogy 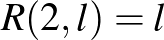, azaz ebben az esetben Erdős és Szekeres becslése (1.2. tétel) éles.

A eset már sokkal érdekesebb. Ekkor az a kérdés, hogy hány csúcs esetén tudunk egy 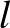-méretű független halmazt garantálni minden háromszögmentes gráfban. Erdős és Szekeres tétele szerint 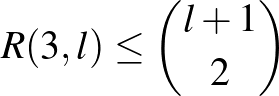. Ez a függvény 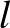-ben négyzetesen növekszik. Az állítást megfordítva azt kapjuk, hogy minden -csúcsú háromszögmentes gráfban van -méretű független halmaz. Vajon ez az állítás javítható? Erre a kérdésre Graver és Yackel pozitív választ adott. Belátták, hogy 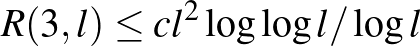, ahol 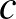konstans. Ez a korlát kicsit kisebb, mint az Erdős–Szekeres-féle négyzetes felső becslés. Az 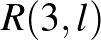Ramsey-számok nagyságrendjét később sikerült teljes pontossággal meghatározni: Léteznek olyan pozitív 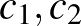konstansok, amelyekre

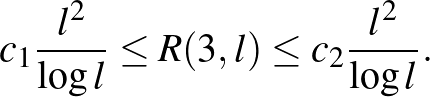
Itt a felső becslés Ajtai Miklós, Komlós János és Szemerédi Endre munkája, [1], míg az alsó becslés Jeong Han Kimtől származik, [8]. Az 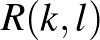Ramsey-számokra semmilyen rögzített 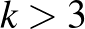értékre nincs ilyen pontos becslésünk.

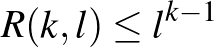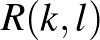Az Erdős–Szekeres tétel szerint , és általános az a nézet, hogy ez a korlát rögzített mellett „majdnem” éles. Vagyis – ahogy a esetben láttuk – valószínűleg más rögzített értékei mellett is csak egy polilogaritmikus faktorral tér el az korláttól, azaz

ahol 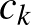egy -tól függő konstans. Ezt a sejtést igazolta most Sam Mattheus és Jacques Verstraete a 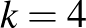esetben. A sejtés továbbra is nyitott minden 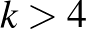értékre.

2.2. tétel. (Mattheus és Verstraete [9]) Van egy olyan pozitív 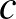konstans, hogy minden 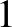-nél nagyobb 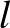egész számra

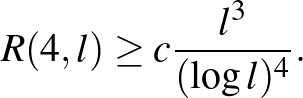
Vegyük észre, hogy míg Campos, Griffiths, Morris es Sahasrabudhe a diagonális Ramsey-számokra adott új felső becslést, addig Mattheus és Verstraete – épp ellenkezőleg – az 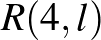Ramsey-számokra talált új alsó becslést. Ennek megfelelően a két bizonyítás struktúrája teljesen más. A felső becslés egy ügyes algoritmusra épül, amely minden 2 színnel élszínezett teljes gráfban talál egy nagy, egyszínű klikket. Az alsó becslés alapja egy konstrukció. Olyan 4-klikk-mentes gráfokat konstruálnak, amelyekben nincs nagy független halmaz. Cikkünk következő két fejezetében e két bizonyítás módszereibe nyújtunk betekintést, de egyiket sem tudjuk teljes egészében bemutatni.

3.  Új felső becslés diagonális Ramsey-számokra

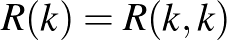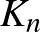Emlékeztetőül, jelöli azt a legkisebb számot, amelyre az -csúcsú teljes gráf, éleit akárhogy színezzük meg két színnel, mindenképp találunk benne egyszínű -méretű klikket, azaz olyan csúcsot, hogy a köztük futó összes él színe megegyezik. A diagonális Ramsey-számok felső becsléséhez rögzítsük 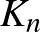éleinek egy színezését pirossal és kékkel, és keressünk egy minél nagyobb egyszínű klikket. A következő egyszerű és klasszikus algoritmus egyszerre keres egy piros és egy kék klikket, közben pedig számon tartja csúcsok azon halmazát, amivel mindkét klikk bővíthető. Az algoritmus utolsó lépésében és valamelyike elég nagy lesz.

A klasszikus algoritmus. Kezdetben és üresek, pedig a gráf összes csúcsának halmaza. Általában arra fogunk figyelni, hogy és legyen piros, illetve kék klikk, amelyet egy tetszőleges csúcsával bővítve még mindig piros, illetve kék klikket kapjunk. Azaz minden -n belüli, és és közötti él legyen piros, továbbá minden -n belüli, és és közötti él legyen kék. Ezek a színezési feltételek kezdetben nyilván teljesülnek, hiszen nincsenek is ilyen élek.

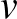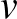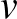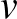Míg el nem fogy, tegyük a következőt. Válasszunk egy tetszőleges csúcsot -ből. -t vegyük ki -ből és vegyük hozzá -hez vagy -hoz. Amennyiben -hez vettük hozzá, hagyjuk ki -ből összes kék szomszédját (vagyis azokat a csúcsokat, amelyeket -vel kék él köt össze). Így a fenti színezési feltételek továbbra is érvényben maradnak. Hasonlóképp, ha -t -hoz vettük hozzá, akkor -ből ki kell hagynunk piros szomszédait. A két lehetőség közül válasszuk azt, amelyik után mérete nagyobb marad (vagy legalábbis nem lesz kisebb).

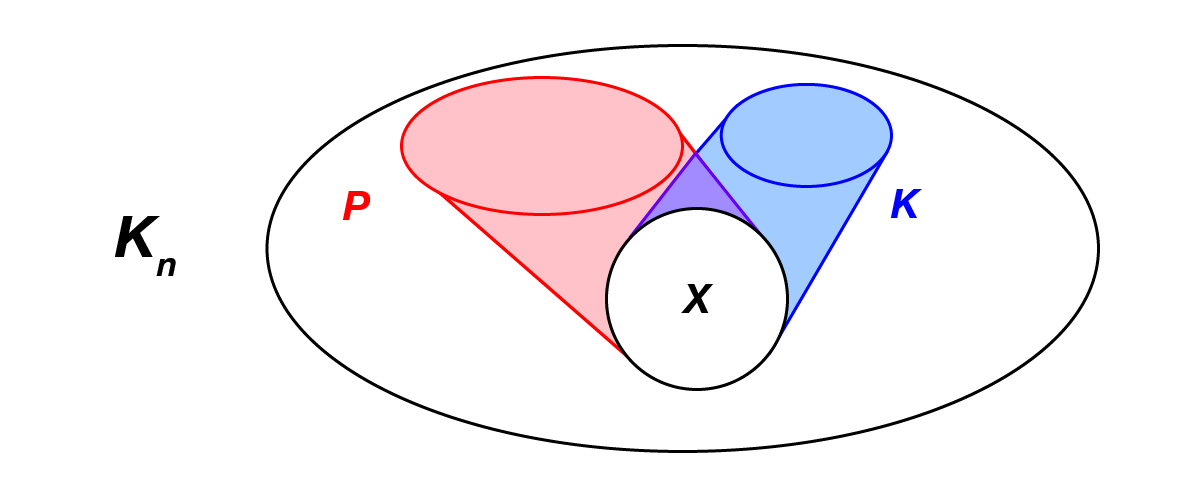
Világos, hogy mérete minden lépésben – a legrosszabb esetben – feleződik, pontosabban 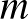-ről legalább 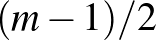-re változik. Ha tehát 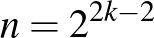csúccsal indítunk, akkor legalább 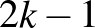lépést tehetünk mielőtt az algoritmus leáll. Következésképp 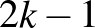lépés után -ben és -ban összesen 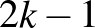csúcs van. A két egyszínű klikk egyike tehát legalább elemű. Ezzel beláttuk, hogy

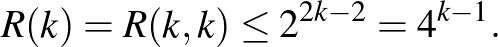
Erdős és Szekeres eredeti felső becslése 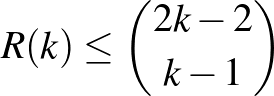volt, ami a mi becslésünknél csak egy árnyalattal erősebb, körül van. Az Erdős és Szekeres eredménye és a friss Campos–Griffiths–Morris–Sahasrabudhe cikk megjelenése közt eltelt majd 90 év alatt a felső becslésen alig sikerült javítani. A legtovább Sah [12] jutott, aki 2023-ban belátta, hogy valamely pozitív konstansra

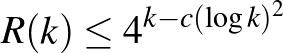
teljesül.

Erdős és Szekeres felső becslésének első exponenciális javítását tehát a nemrég bizonyított 2.1. tétel adja, miszerint létezik egy olyan konstans, amelyre 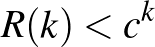teljesül. Ők is egy algoritmust használtak nagy egyszínű klikk keresésére egy -csúcsú élszínezett teljes gráfban. Céljuk az volt, hogy a fenti klasszikus algoritmus által talált 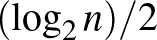-méretű egyszínű klikknél lényegesen nagyobbat találjanak. Itt a „lényegesen nagyobb” azt jelenti, hogy valamilyen konstansra legalább 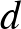-szer ekkora méretű egyszínű klikket kell találni. Ez felel meg a Ramsey-szám exponenciális javításának. Campos, Griffiths, Morris és Sahasrabudhe algoritmusa hasonlít a klasszikus algoritmusra, de annál sokkal összetettebb, ezért csak vázlatosan ismertetjük.

Ismét a 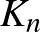teljes gráfból indulunk ki, amelynek minden élét pirossal vagy kékkel színeztük.

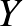Az új, javított algoritmus. Az algoritmus négy diszjunkt csúcshalmazzal dolgozik, ezek , , és . , és szerepe hasonló, mint a klasszikus algoritmusnál. Vagyis piros klikk, kék klikk, pedig olyan csúcsokból áll, amelyekből -hez piros, -hoz pedig kék élek vezetnek. szerepe azonban nem szimmetrikus. Innen -hez csak piros élek vezetnek, viszont az és közötti élek színére nincs megkötés. Kezdetben a gráf csúcshalmazát két egyenlő részre bontjuk, ezek lesznek és , és pedig üresek.

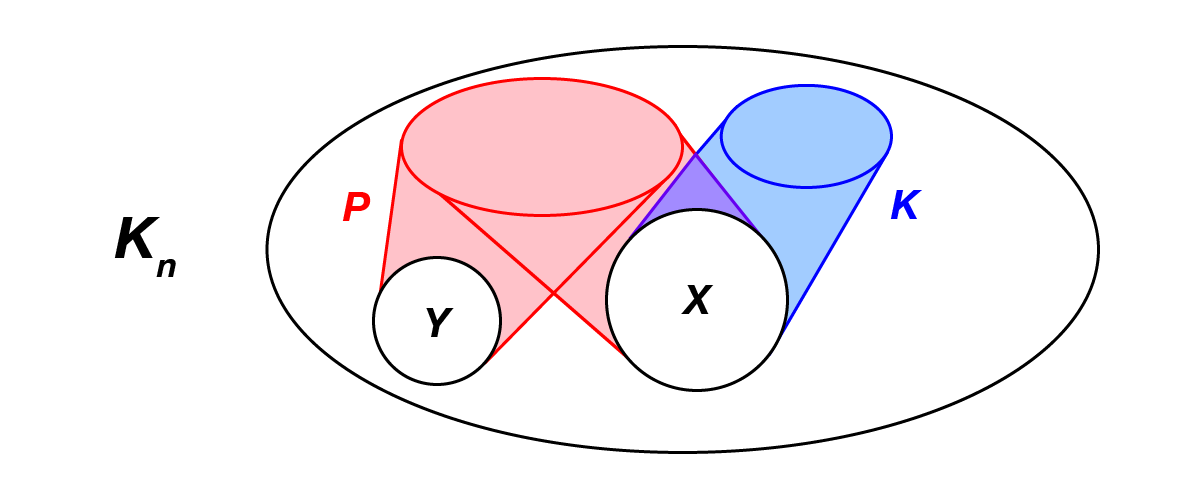
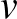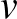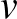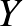A klasszikus algoritmushoz hasonlóan minden lépésben kiveszünk -ből egy csúcsot, és hozzáadjuk -hez vagy -hoz. Ha -hoz adjuk hozzá, akkor -ből elhagyjuk piros szomszédjait, ha -hez vesszük hozzá, akkor kék szomszédjait kell kihagynunk mind -ből, mind -ből.

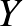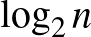Az algoritmus legfontosabb döntése, hogy mikor melyik lépést választjuk, de mielőtt erre rátérnénk, nézzük meg, hogy az halmaz bevezetése miben segíthet. Akárcsak a klasszikus algoritmusnál, könnyű biztosítani, hogy mérete lépésenként a legrosszabb esetben feleződjön, és így csak körülbelül lépés után fogyjon el. Ekkorra tehát 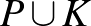mérete 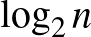körül lesz. A klasszikus algoritmus 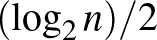-méretű egyszínű klikket talál, és ha és közül az egyik lényegesen nagyobb mint a másik, akkor már el is értük a célunkat, hogy nagyobb egyszínű klikket találjunk. 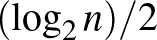Ha mind , mind mérete körül van, akkor elővesszük az halmazt és választunk egy olyan értéket, amelyre . 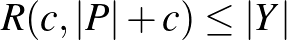Itt persze tudnunk kéne ezt a Ramsey-számot, de ehelyett Erdős és Szekeres felső becslését használjuk. Ekkor 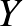-ban vagy találunk egy 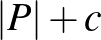-méretű kék klikket, vagy egy 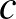-méretű piros klikket, amelyet -hez hozzávéve ismét van egy 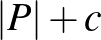-méretű egyszínű klikkünk. Tehát, ha 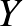mérete elég nagy, akkor ezzel a módszerrel célt érünk, 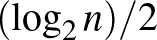-nél lényegesen nagyobb egyszínű klikket találunk.

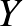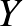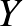De vajon mekkora lesz az halmaz? mérete csak azokban a lépésekben csökkent, amikor -t növeltük. Ha a teljes gráf élszínezése véletlen lenne, akkor azt várnánk, hogy minden ilyen lépésben körülbelül felére csökken, és a legvégén körüli, ami bőven elég ahhoz, hogy a fenti gondolatmenet működjön. Sajnos azonban nem tehetjük fel, hogy a gráfszínezés véletlen. Ha például és között túl sok kék él van, akkor nehéz elkerülni, hogy 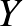mérete túl gyorsan csökkenjen.

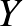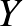Az egyes lépések megválasztásánál három dologra kell figyelnünk, nevezetesen arra, hogy a tervezett lépés milyen mértékben csökkenti és méretét, valamint hogy miként változtatja az és közötti élek között a pirosak arányát. Szimmetria okán feltehetjük, hogy az arány kezdetben legalább 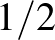(ellenkező esetben felcseréljük a két színt, ami feladaton nem változtat). Vigyáznunk kell, hogy az algoritmus futása során se menjen ez az arány sokkal 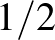alá. Az algoritmus akkor enged egy csúcsot -ből -be rakni, ha ez az egyik értéket sem csökkenti túlságosan. -ből -ba tipikusan egyszerre sok csúcsot rakunk át, de csak akkor, ha ezek együtt sem csökkentik nagyon ezeket az értékeket. 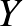Ha ezen lépések egyikére sincs lehetőség, akkor mégis egyetlen -beli csúcsot rakunk át -ba, de ezt a csúcsot olyan ügyesen lehet megválasztani, hogy miközben mérete alig csökken, a piros élek aránya és között jelentősen növekszik.

De ezzel még nem értünk a bonyodalmak végére! Az ily módon javított, bonyolult algoritmusnak már majdnem sikerül nagyobb egyszínű klikket találnia, mint a klasszikus algoritmusnak, de nem egészen. Épp a diagonális esetben közvetlenül nem tudunk vele javítani a Ramsey-számokra adott felső becslésen. Viszont azokra az 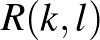Ramsey-számokra, ahol 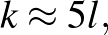a fenti algoritmus egy variánsa már lényegesen javít Erdős és Szekeres becslésén. Ha az algoritmus végén ezt a javított becslést alkalmazzuk 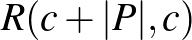-re, akkor már a diagonális Ramsey-számokra is a korábbinál lényegesen jobb becslést nyerünk.

4.  Új alsó becslés az 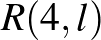Ramsey-számokra

Ha a logaritmikus faktoroktól eltekintünk, Mattheus és Verstraete tétele (2.2 Tétel) azt mondja ki, hogy van olyan gráf, amelyben nincs se 4-csúcsú klikk, se 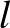-méretű független halmaz, mégis majdnem 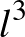csúcsa van. Adott tulajdonságokkal rendelkező gráfok létezését alapvetően két teljesen különböző módon lehet bizonyítani. A legegyszerűbb, közvetlen módszer a feltételeknek megfelelő gráfok konstruálása. Gyakran valamilyen algebrai jellegű struktúrából indulunk ki, abból készítünk egy gráfot, és az eredeti struktúra algebrai tulajdonságait felhasználva belátjuk, hogy az így konstruált gráf rendelkezik az elvárt tulajdonságokkal. A másik út az Erdős által kidolgozott ún. véletlen módszer [5,2]. Az eljárás lényege, hogy explicit konstrukció helyett – egy megfelelően választott eloszlás szerint – véletlenül választunk egy gráfot, amiről aztán megmutatjuk, hogy pozitív valószínűséggel teljesíti az elvárt tulajdonságokat.

Lássunk egy példát mindkét típusú bizonyításra!

Először azt vizsgáljuk, hogy hány éle lehet egy -csúcsú gráfnak, amelyben nincs 4-hosszúságú kör. Induljunk ki egy véges projektív síkból, ezek később is fontos szerepet játszanak majd. Egyelőre elég annyit tudni róluk, hogy egy projektív sík pontokból áll, a pontok meghatározott részhalmazai ún. egyeneseket alkotnak, amelyekre teljesül, hogy két adott pontot egyetlen közös egyenes tartalmaz, míg bármely két egyenes egy pontban metszi egymást. Véges projektív sík esetén véges sok pontunk van. Minden véges projektív síknak van egy rendje, vagyis egy olyan 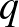egész szám, amelyre teljesül, hogy mind a pontok, mind az egyenesek száma 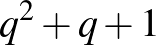, és minden egyenes pontból áll. A síkból egy páros gráfot készítünk, amelynek a csúcsai a sík pontjai és egyenesei. Ha egy egyenes tartalmaz egy pontot, akkor a nekik megfelelő csúcsokat összekötjük egy éllel. Az ilyen módon keletkezett gráfnak 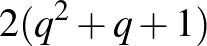csúcsa és éle van. Egy 4-hosszú kör ebben a gráfban két egyenest reprezentálna, amelyeknek két közös pontjuk van. Mivel ilyen konfiguráció egy véges síkban – definíció szerint – nincs, a konstruált gráfban sincs 4-hosszú kör. Nem nehéz megmutatni, hogy 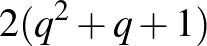-pontú, 4-hosszú körmentes páros gráfban nem is lehet ennél több él, azaz ez a konstrukció optimális.

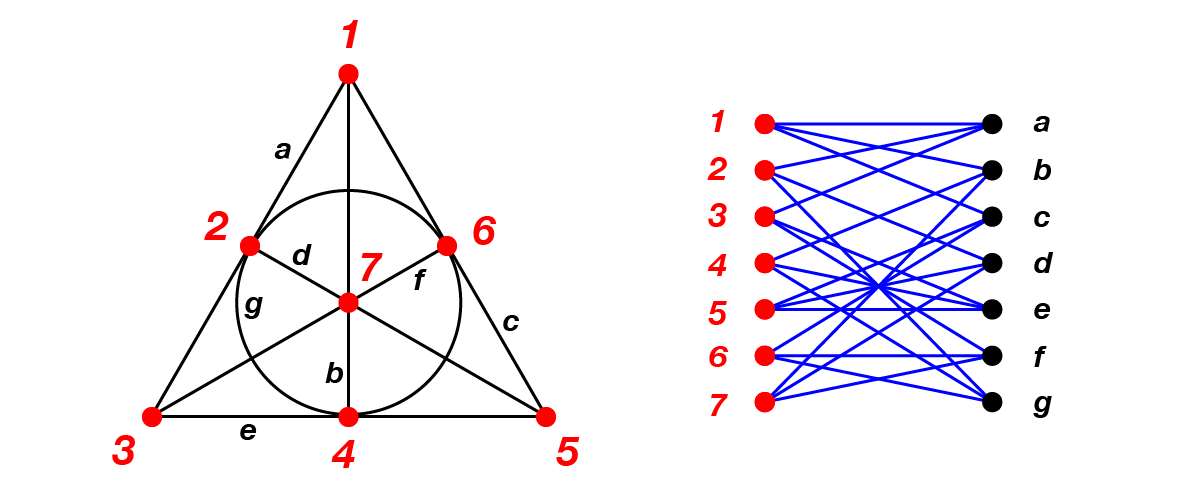
A q = 2-rendű, úgynevezett Fano-sík, és a belőle kapott páros gráf.

A legjobb alsó becslést diagonális Ramsey-számokra a véletlen módszer adja. Tekintsünk egy -csúcsú 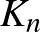teljes gráfot, amelynek éleit – egyenletes eloszlás szerint – véletlenszerűen pirosra vagy kékre színeztünk. Könnyű kiszámolni, hogy az egyszínű -klikkek várható száma pontosan 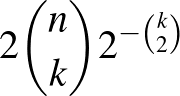. Ha értékét megfelelően választjuk közelében, akkor ez a szám 1-nél kisebb lesz, amiből következik, hogy van egy olyan színezés, amelyben egyáltalán nincs egyszínű -klikk. Így tehát

Ez az elegáns bizonyítás Erdőstől [4] származik 1947-ből. Ennél nagyságrendileg jobb becslés azóta sem ismert. Kim [8] alsó becslése az 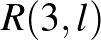Ramsey-számokra is a véletlen módszert használja, csak az eloszlás, amely szerint a véletlen gráfot választja egy bonyolult véletlen folyamat eredménye, nem pedig az egyenletes eloszlás.

Tételük bizonyításához Mattheus és Verstraete ügyesen kombinálják a fenti két módszert. Kiindulási pontjuk ún. Hermite-féle unital. Az unital egy a projektív síkhoz sokban hasonló struktúra: ez is egy véges ponthalmazból és ennek bizonyos kijelölt – egyenesnek nevezett – részhalmazaiból áll. Mint a projektív sík esetében, itt is elvárjuk, hogy bármely két pont pontosan egy közös egyenesben szerepeljen, de most nem minden egynes-párnak kell közös pontot tartalmaznia. Egy -rendű unitálban pont van és minden egyenes pontból áll. Unitalt legegyszerűbben egy algebrailag definiált 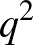-rendű projektív sík egy – ugyancsak algebrailag meghatározott – részhalmazaként lehet megadni. Az így konstruált unitalt Hermite-félének nevezzük. A Hermite-féle unital érdekes, szimmetrikus struktúrájára már korábban felfigyeltek a matematikusok. O'Nan bizonyította [10], hogy egy Hermite-féle unitalban nincs 4 olyan egyenes, amelyek páronként metszik egymást és a 6 páronkénti metszéspont mind különböző.

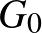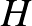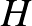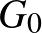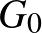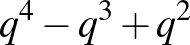Mattheus és Verstraete úgy konstruál egy gráfot egy Hermite-féle unitalból, hogy egyenesei lesznek csúcsai, míg az élek az olyan egyeneseknek megfelelő csúcsokat kötik össze, amelyek „metszik” egymást, azaz van közös pontjuk. A fentiek alapján könnyen kiszámolható, hogy -nak csúcsa van és 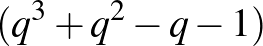-reguláris, vagyis minden csúcsa ennyi másik csúccsal szomszédos. Vegyük észre, hogy O'Nan tétele bizonyos 4-csúcsú klikkek nemlétezését mondja ki 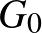-ban. Mi olyan gráfot szeretnénk konstruálni, amelyben nincs 4-csúcsú klikk, ezért O'Nan tétele „jó hír”. De sajnos ez nem elég. Könnyen kiszámolható, hogy az unital minden pontját pontosan 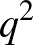egyenes tartalmazza, és ezek egyetlen nagy klikket alkotnak 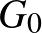-ban. Tehát 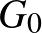messze nem mentes 4-méretű klikkektől. Ezért meg kell „ritkítani”. Mint észrevettük, 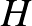minden pontjához tartozik 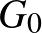-ban egy 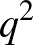-méretű klikk. Cseréljük ki most az összes ilyen klikket egy-egy teljes páros gráfra! O'Nan tételéből könnyen igazolható, hogy az így kapott 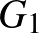gráf már nem tartalmaz 4-méretű klikket. Itt használjuk először a véletlen módszert: 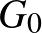minden nagy klikkjének csúcsait véletlenül osztjuk két részre és a klikkből csak a két rész közötti éleket hagyjuk meg.

Nézzük most a független halmazok méretét a gráfjainkban! 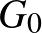-ban egy független halmaz diszjunkt egyenesekből áll, így mérete nem lehet nagyobb, mint

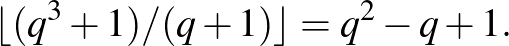
Az jó, hogy van egy becslésünk a független halmazok méretére, de sajnos nem elég erős. 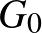csúcsszáma csak négyzetes ebben a korlátban, márpedig nekünk az kéne, hogy megközelítőleg köbös legyen. Ráadásul 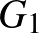ritkább gráf, mint 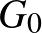, keletkezhetnek benne újabb független halmazok, akár sokkal nagyobbak is. Például  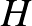egy pontjához tartozó 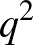-méretű 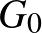-klikkből egy teljes páros gráfot csináltunk, amelynek mindkét oldala független halmaz. Tehát 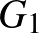-ben sok új 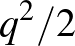-méretű független halmaz van. Mattheus és Verstraete azonban belátják, hogy ha 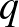-t növeljük, akkor 1-hez tartó valószínűséggel kevés 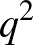-nél nagyobb független halmaz keletkezik, olyan pedig egy sem, amelyik ennél sokkal nagyobb lenne.

Vagyis jó eséllyel 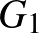-ben sem lesz sokkal nagyobb független halmaz, mint 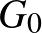-ban, de – mint láttuk – ezen gráfok mérete nem elég nagy a független halmazaik méretéhez képest. Ezt a problémát Mattheus és Verstraete véletlen mintavétellel orvosolják. 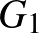csúcsait egymástól függetlenül azonos  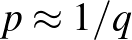körüli valószínűséggel választják be a mintába. 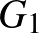-nek a kiválasztott csúcsok által feszített részgráfját jelöljük -vel. Mivel már -ben sem volt 4-méretű klikk, nyilván 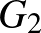-ben sem lesz. 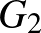méretét nem ismerjük pontosan, de csúcsszáma túlnyomó valószínűséggel körülbelül 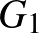csúcsszámának a 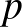-szerese, azaz nagyságrendileg 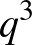. Egy adott 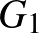-beli független halmaz mérete 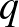-ban legfeljebb négyzetes, és túlnyomó eséllyel ennek körülbelül a 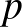-szerese kerül be 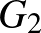-be, ami már legfeljebb lineáris 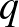-ban. A bizonyítás legtechnikaibb része annak belátása, hogy nagy valószínűséggel egy majdnem ilyen erős korlát teljesül egyszerre 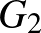összes független halmazára. Ezzel azonban el is jutottunk a bizonyítás végére, hiszen látjuk, hogy 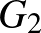-ben biztosan nincs négyes klikk, és csúcsainak száma nagy eséllyel 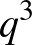körül van, míg legnagyobb független halmaza alig több, mint 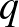csúcsból áll.

5.  További kutatási irányok

Biztosak lehetünk abban, hogy a fent vázolt eredmények nyomán megújul az érdeklődés a Ramsey-számok nagyságrendjének vizsgálata iránt. A közeljövőben a témában további jelentős előretörésre számíthatunk. A 2.1. tétel ugyan exponenciális javítást ad Erdős és Szekeres a diagonális Ramsey számokra vonatkozó felső becslésére, de a tételben szereplő 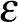értéke nagyon kicsi. A bizonyítás módszereinek további csiszolásával valószínüleg ez az érték növelhető. Még érdekesebb lenne, ha az Erdős-féle alsó becslést is sikerülne exponenciális mértékben javítani, de ehhez feltehetően egészen másfajta módszerekre lesz szükség.

A 2.2. tétel javítására is van esély, hiszen az 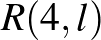Ramsey-számokra ismert alsó és felső becslések egy polilogaritmikus faktorral eltérnek egymástól. A következő kézenfekvő feladat az számok vizsgálata lehet, vagy – általánosabban – az 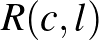számoké nagyobb, konstans értékeire.

Ebben a cikkben egyáltalán nem érintettük a hipergráf Ramsey-számok kérdését, pedig ott még több a megoldatlan probléma, hiszen már 3-uniform hipergráfokra is sokkal távolabb vannak egymástól az ismert alsó és felső becslések, mint gráfok esetén.

Köszönetnyilvánítás

A cikk megírásában segítséget jelentett az GeoScape és ERMiD ERC grantok valamint a K-131529, K-132696 és SSN-135643 számú NKFIH grantok által nyújtott támogatás.

Irodalomjegyzék

[1] M. Ajtai, J. Komlós, and E. Szemerédi: A note on Ramsey numbers, Journal of Combinatorial Theory, Series A 29 (3) (1980), 354–360.

[2] N. Alon and J. Spencer: The Probabilistic Method, John Wiley & Sons, New York, 2015.

[3] M. Campos, S. Griffiths, R. Morris, and J. Sahasrabudhe: An exponential improvement for diagonal Ramsey, Preprint arXiv:2303.09521.

[4] P. Erdős: Some remarks on the theory of graphs, Bull. Amer. Math. Soc. 53 (4) (1947), 292–294.

[5] P. Erdős and J. Spencer: Probabilistic Methods in Combinatorics, Akadémiai Kiadó, Budapest, 1974.

[6] P. Erdős and G. Szekeres: A combinatorial problem in geometry, Compositio Math. 2 (1935), 463–470.

[7] J. E. Graver and J. Yackel: Some graph theoretic results associated with Ramsey's theorem, Journal of Combinatorial Theory 4 (2) (1968), 125–175.

[8] J. H. Kim: The Ramsey number 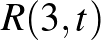has order of magnitude 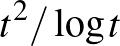, Random Structures & Algorithms 7 (3) (1995), 173–207.

[9] S. Mattheus and J. Verstraete: The asymptotics of 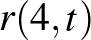, Annals of Mathematics 199 (2) (2024), 919–941.

[10] M. O'Nan: A characterisationof as a permutation group, Math. Z. 127 (1972), 301–314.

[11] F. P. Ramsey: On a problem of formal logic, Proc. London Math. Soc. 30 (1930), 264–286. Also in Classic Papers in Combinatorics, Birkhäuser, Boston, 1987, 1–24.

[12] A. Sah: Diagonal Ramsey via effective quasirandomness, Duke Mathematical Journal 172 (3) (2023), 545–567.

[13] P. Frankl and R. M. Wilson: Intersection theorems with geometric consequences, Combinatorica 1 (1981), 357–368.