A 100 éve született René Thom tudományos hagyatéka

Mottó: „Akkor, amikor világszerte annyi tudós számol, nem kívánatos-e hogy néhányan, akik tudnak, álmodjanak?” (R. Thom)

2023 szeptemberében volt René Thom, a neves és sokoldalú francia geométer és topológus születésének századik évfordulója. Ebből az alkalomból eseménysorozattal emlékezett meg róla a párizsi Francia Tudományos Akadémia és volt munkahelye, az Institut des Hautes Études Scientifiques (IHÉS) kutatóintézet. Beszámolót készítettünk az ünnepi alkalmakról.

Emlékülés a Francia Tudományos Akadémián

Szeptember 19-én, a Francia Tudományos Akadémia épületében nem szakmai közönségnek szóló megemlékezés zajlott¹ a tudós családjának jelenlétében. Ennek felvezetőjeként Étienne Ghys matematikus, az Akadémia örökös titkára vázolta fel Thom nagyívű tudományos munkásságát és pályáját: miközben a matematikában megalkotta a kobordizmusok elméletét valamint a népszerűvé vált katasztrófaelméletet, emellett foglalkozott biológiai, nyelvészeti és filozófiai kérdésekkel is, olyannyira, hogy több könyvet jelentetett meg e témákról. A matematikában az ő nevéhez fűződik a leképezések transzverzalitásának [3] és generikusságának fogalma is [4]. Ghys több Thommal készült interjúrészletet lejátszott, amelyekből kiderült többek között az, hogy – jóllehet a kutatás hatalmas szabadságérzetet nyújtott neki –, a kutatópályája kezdeti útkeresését elvesztegetett időként élte meg. Azt is megtudhattuk, hogy Thomnak az 1958-ban a kobordizmuselméleti munkájáért nyert Fields-érme a véleménye szerint maga helyett Arisztotelésznek járt volna.

Ghys felvezetőjét Patrick Popescu-Pampu matematikus előadása követte (aki szoros kapcsolatot ápol a Rényi Alfréd Matematikai Kutatóintézetbeli szingularitáselméleti iskolával, mint Némethi András többszörös társszezője és rendszeres vendége). Kifejtette, hogy Thom alapvető érdeklődési területe az alakok egymásba való átváltozása lett a matematikában (pl. Morse-elmélet) éppúgy, mint a biológiában (morfogenezis, azaz az alakok kialakulása és fejlődése). Ezek kapcsán szót ejtett a Thom által megteremtett struktúrális stabilitás fogalmáról: hétköznapi szóhasználattal élve, ez a jelenség akkor áll fenn, ha a formák változásában nem következik be változás. Ezt a jelenséget egy negyedrendű potenciálárok több (alacsonyabb rendű) árokká való szétválásával illusztrálta. Ezután részletesen számba vette Thom elméletének [5] 7 „katasztrófáját” (azaz, legfeljebb 4 kodimenziós stabil szingularitását), úgymint: hajtás, csúcs (az alábbi ábrán), fecskefarok, pillangó, hiperbolikus, elliptikus és parabolikus köldökpont², és ezek körkörös egymásba való átmenetét.

Csúcs

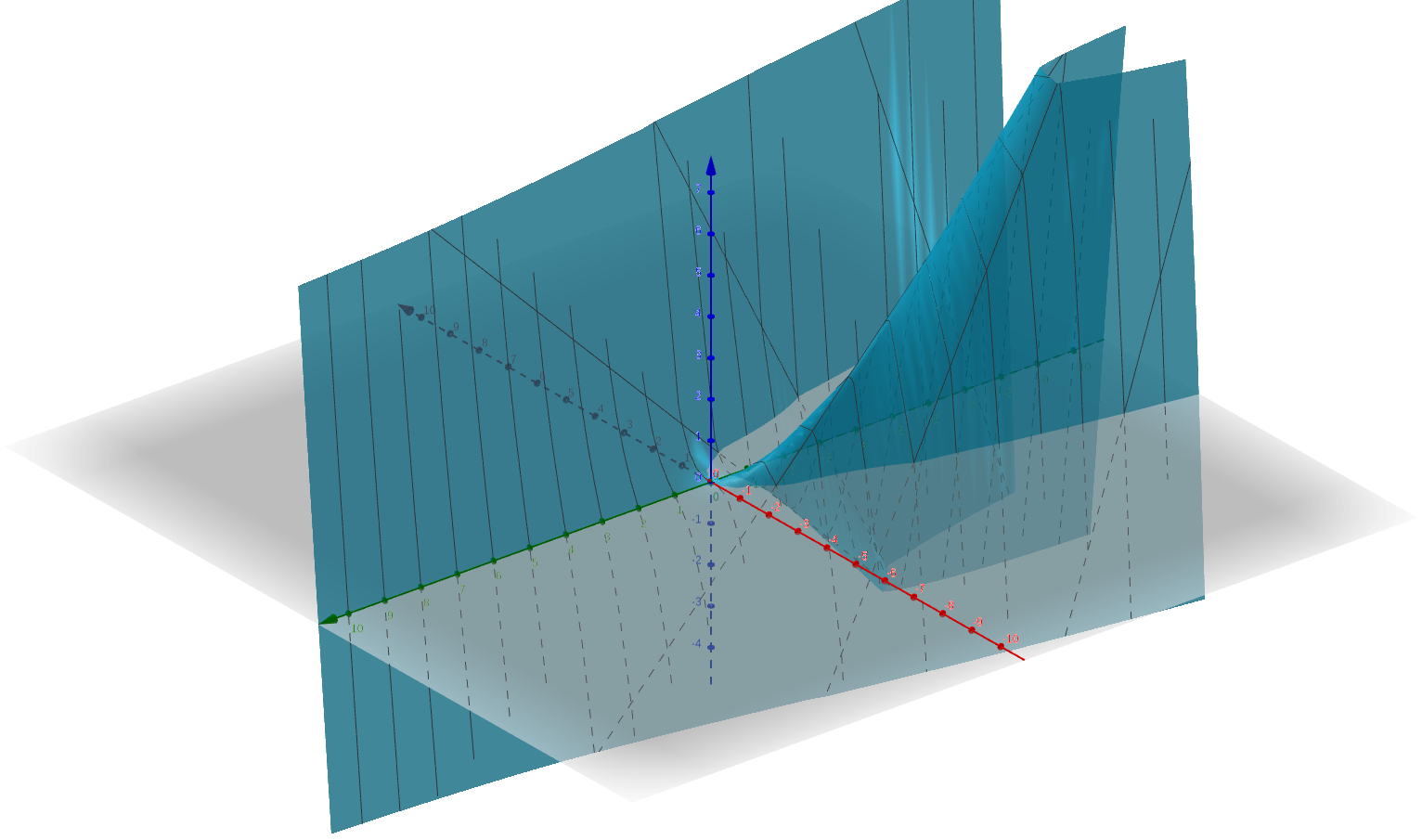
Végül bemutatott egy részletet a híres filmrendező, Jean-Luc Godard Thommal készült dokumentumfilmjéből, amelyben a tudós a rendező egy kérdésére válaszolva azt a véleményét fejtegeti, hogy a definíciója alapján a mindennapi élet bizonyos jelenségei tekinthetők „katasztrófának”: a matematikai bifurkációkhoz hasonló mintákat találunk bennük. Mint ebből a részletből is kitűnik, Thom egész életében kereste a matematika kapcsolódását más tudományokhoz, a művészethez és a mindennapi élethez – attól sem riadva vissza, hogy provokatív kijelentései miatt időnként más tudósokkal, művészekkel konfliktusba kerüljön. Különösen kiélezett hangnemű vitát folytatott a tudomány determinisztikus létéről való nézeteltérésük miatt Ilya Prigogine Nobel-díjas vegyésszel, akit egyik írásában [7] egyszerűen „csalónak” minősített. Prigogine nézete szerint ugyanis a determinisztikus tudományok kora leáldozott, az ilyen folyamatok a mai tudományban inkább kivételnek számítanak, mint gyakorinak, míg Thom ragaszkodott a tudomány determinisztikus jellegéhez, és nézete szerint különbséget kell tenni folyamatok leírhatósága és előrejelezhetősége között.

A harmadik előadó Annick Lesne biológusnő volt, aki ismertette Thom alakfejlődéssel kapcsolatos meggondolásainak visszatükröződését a modern biológián belül. Mint elmondta, Thomra főleg D'Arcy Thompson „On growth and forms” és Conrad Hal Waddington „The strategy of the genes” című munkái gyakoroltak hatást. Kiemelte, hogy Thom vigyázott rá, nehogy a makroszkopikusan alkalmazható geometriai gondolatmeneteit mikroszkopikus (sejt-szintű) kérdésekre alkalmazzák.

Végül, az utolsó előadást Fabrice Hyber művész tartotta, Thomnak a művészetekre gyakorolt hatásáról. Megtudhattuk tőle, hogy (némileg talán meglepő módon) Salvador Dali festőművész rajongott Thomért, és életének utolsó évében több képét (köztük életének legutolsó képét) is Thomnak ajánlotta.

A hozzászólásokban további érdekes részleteket tudhattunk meg a tudós életéről. David Ruelle fizikus, aki az IHÉS-en vele szomszédos irodában dolgozott, felelevenítette gyakori beszélgetéseiket, amelyekből kiderült, hogy mennyire nem értenek egyet például a valószínűségszámítás kvantumfizikabeli szerepéről. Thom rendszerint a (korábban mások mellett Albert Einstein által is képviselt) determinisztikus, „valószínűség-mentes” fizika mellett érvelt, míg Ruelle (a modern statisztikus fizika egyik legjelesebb képviselője) ez ellen. Kiemelte azonban, hogy nézeteik különbözőségeinek ellenére személyes kapcsolatuk kitűnő volt. Étienne Ghys ennek kapcsán megemlített egy másik érdekességet, miszerint Thom és a vele egyidőben szintén az IHÉS-en tevékenykedő Alexander Grothendieck algebrai geométer között ki sem alakult érdemi tudományos párbeszéd. Ennek oka minden bizonnyal különböző hozzáállásukban gyökerezett: míg Thom más tudományokban is előszeretettel alkalmazott geometriai módszereket, addig Grothendieck ezzel éppen ellenkezőleg a geometria algebrizálásán munkálkodott.

Emlékkonferencia az IHÉS-en

Szeptember 20-22. között nemzetközi konferenciát rendeztek az IHÉS-en Thom kutatási területeiről³. Az elhangzott előadások közül itt csupán azokat ismertetjük, amelyek szorosan kapcsolódnak Thom matematikai munkájához.

Emmanuel Giroux előadásából megtudhattuk többek között, hogy a Morse-elméletet megalapozó cikk [2] nagyjából Thommal egyidőben született meg: ugyan csak 1925-ben közölték, ám már 1923 decemberében benyújtásra került. Ez az elmélet alapvetően meghatározó volt Thom egész matematikai gondolkodásmódjában. Erre például megemlítette Thom 1957-es ötletét (amely nyomtatásban itt található meg: [1]), amelyben Morse-elméleti módszerrel látja be Lefschetz tételét komplex projektív varitások hipersík-metszetének homológiacsoportjairól.

Dennis Sullivan (a 2022. évi Abel-díj kitüntetettje) előadásának első részében a szinguláris sokaságok lokális alakjáról beszélt Thom [6] cikkét felidézve. Később áttért Thomnak a Steenrod-kérdésre adott példájára: ez egy olyan 7-dimenziós homológiaosztály egy 10-dimenziós sokaságban, amely semmiképpen sem reprezentálható mint valamely 7-sokaság képe.

Daniel Bennequin előadásában – Thom nyomán – az információ és a topológiai bonyolultság kapcsolata mellett érvelt, ezáltal kapcsolódva a pszichológiában Roger Shepard alapította irányzathoz. Említést tett Hermann Grassmann munkásságáról is, aki Thomhoz hasonlóan egyaránt alkotott a matematikában (az ő munkájából eredt a lineáris algebra későbbi szabatos megalapozása Giuseppe Peano és Hermann Weyl által), a nyelvészetben (szanszkrit–német szótár és a Rigvéda német fordítása) és a pszichológiában (a színek keverése alapszínekből és percepciójuk). Előadása végén ismertette saját kutatásainak eredményét a sztochasztikus információ topológiai értelmezéséről.

Az esemény fénypontjaként Jean-Pierre Bourguignon, az IHÉS korábbi igazgatója, felidézte Thom életútjának fő állomásait (Montbéliard, Strasbourg, Bures-sur-Yvette), személyes visszaemlékezéseket olvasott fel pályatársaktól és tanítványoktól, fényképeket és videófelvételeket játszott le életéről és az általa inspirált műalkotásokról.

Irodalomjegyzék

: [1] A. Andreotti, T. Frankel, The Lefschetz Theorem on Hyperplane Sections, Ann. Math. (3) 69 713–717.

[2] M. Morse, Relations between the critical points of a real function of n independent variables, Trans. Amer. Math. Soc. 27 (1925), no.3, 345–396.

[3] R. Thom, Quelques propriétés globales des variétés différentiables Comment. Math. Helv.28 (1954), 17–86.

[4] R. Thom Les singularités des applications différentiables Séminaire Bourbaki 3 (1956), Exp. No. 134, 357–369. Société Mathématique de France, Paris

[5] R. Thom, Topological models in biology Topology, 8 (1969) pp. 313–335.

[6] R. Thom, Ensembles et morphismes stratifiés, Bull. Amer. Math. Soc. 75 (1969), 240–284.

[7] R. Thom, Halte au hasard, silence au bruit, Le Débat 1980/3 (no. 3.), 119–132.

Szabó Szilárd
Budapesti Műszaki Egyetem, Matematika Intézet