Neumann-emlékülések Budapesten és New Yorkban

Neumann János szobra Budapesten, a XI. kerületi Infoparkban, Szathmáry Gyöngyi alkotása. (Készítette: Both Előd a(z) magyar Wikipédia projektből, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=47207314)

2023-ban ünnepli a világ Neumann János születésének 120-adik évfordulóját. A megemlékezésből természetesen a Magyar Tudományos Akadémia sem maradt ki. Szeptember 14-én az MTA támogatásával a Neumann János Számítógéptudományi Társaság által szervezett egész napos konferenciának adott otthont a Széchenyi István téri székház. 

Matematikai programmal pedig a Rényi Alfréd Matematikai Intézet készült; ahol négy előadással emlékeztünk Neumann János matematikai munkásságának egy-egy szeletére. Ezek témái a halmazelmélet, a matematikai logika, az ergodelmélet illetve az operátoralgebrák elméletének területeire estek. Az eseményről a Rényi Intézet Neumann120 honlapja tájékoztat, és mind a négy előadás visszanézhető a Rényi Video Portálján. Közülük itt az elsőt ismertetjük.

Ennek előadója Alain Connes volt, aki a 20. század második felének és jelen korunknak is egyik legkiemelkedőbb matematikusa. Alan Connes az operátoralgebrák elméletében végzett alapvető jelentőségű munkáiért és a nemkommutatív geometria területének létrehozásáért 1983-ban Fields-érmet kapott. Eredményei nagy hatásúak a kvantum- és részecskefizika bizonyos területein is, valamint az általa kidolgozott eszközök a Riemann-hipotézissel kapcsolatos kutatásokban is komoly jelentőséggel bírnak.

Előadásában azt mutatta be, hogyan vezettek és milyen szerepet játszottak Neumann Jánosnak az operátoralgebrák elméletét megalapozó gondolatai a nemkommutatív geometria megszületésében.

Az előadás első része a Neumann-faktorokról szólt (ezen operátoralgebrák közös jellemzője, hogy algebrai centrumuk triviális). Az előadó elmondta, hogyan merült fel a faktorok fogalma Murray és Neumann 1936 és 1943 között írt „On rings of operators” címmel megjelent, az operátoralgebrák elméletét megindító cikksorozatának első darabjában, a kvantummechanikai rendszerek részrendszereinek matematikai leírásával kapcsolatban.

Neumann és társszerzője a faktorokat három csoportba sorolta. Szeparábilis Hilbert-tér esetén az I. típusúak pontosan a teljes mátrixalgebrák illetve a Hilbert-tér teljes operátoralgebrája. A II. típusú faktorok már jóval komplikáltabbak. Ilyen faktoron megadható egy ún. dimenziófüggvény, amelynek az értékei nem diszkrétek, hanem „folytonosak”, a vagy a intervallumot futják be. A III. típusba eső faktorok pedig azok, amelyek nem tartoznak az I-II. csoport egyikébe sem. Hogy egyáltalán létezik ilyen faktor, azt Neumann Jánosnak 1940-ben sikerült bizonyítania. (A történet hazai vonatkozásaként említjük azt a nagy jelentőségű eredményt, amit az akkor Szegeden frissen doktorált Pukánszky Lajos ért el 1956-ban. Nevezetesen példát adott két nem izomorf III. típusú faktorra. Az eredményt a Publ. Math. (Debrecen) folyóirat közölte.)

Nagy lendületet adott a III. típusú faktorok mély vizsgálatához Araki egy 1964-ben publikált munkája, e szerint az elméleti fizikában fellépő Neumann algebrák többsége éppen III. típusú.

A fiatal Alain Connes igazi áttörést jelentő eredményeket ért el a területen. Az előadásban elhangzott, hogy először egy kvantum statisztikus fizikai probléma kapcsán Tomita és Takesaki eredményeinek segítségével 1972-ben, doktori értekezésében megmutatta, hogy valamennyi Neumann-algebra rendelkezik egy bizonyos belső dinamikával: automorfizmusainak van egy olyan kitüntetett egyparaméteres csoportja, ami lényegében egyértelműen meghatározott az illető algebra által. Erre az eredményre támaszkodva, Neumann-algebrákra vonatkozóan felfedezett két algebrai invariánst, illetve kapcsolatot talált a III. típusú algebrák és II. típusúak között. 1976-ra pedig eljutott az ún. hipervéges III. típusú faktorok (ezek olyanok, amelyeket végesdimenziós részalgebráinak egy bővülő sorozata generál) teljes klasszifikációjáig. Ezek a III_λ faktorok, ahol (pontosabban, a III₁ típusú hipervéges faktor egyértelműségének kérdése nyitva maradt, azt Haagerup tisztázta 1987-ben). Connes ezen eredményeit a 20. századi matematika csúcsteljesítményei között szokás említeni. (További hazai vonatkozásként megjegyezzük, hogy Connes a fentiekhez vezető munkáinak egy darabját a szegedi Actában publikálta. Az 1975-ben beküldött cikk 1977-ben jelent meg.)

Az előadás második része operátoralgebráknak a differenciálgeometriában való megjelenéséről, a nemkommutatív geometria születéséről szólt. Nevezetesen Alain Connes-nak arról az 1978-ban publikált eredményéről, amely szerint sokaságokon adott fóliázások természetes módon generálnak ún. véletlen operátorok alkotta algebrákat (ezen véletlen operátoroknak nevezett objektumok pontosabban operátorseregek, amiknek elemei a fóliázás leveleihez tartozó 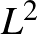-tereken ható operátorok). Az említett algebrák Neumann-algebrákként tekinthetők, és kiderült, hogy már az egyszerű fóliázásokhoz is bonyolult ilyen algebrák társulnak. Sőt, minden III. típusú faktor fellép valamilyen fóliázáshoz kapcsolódóan. Ezek az eredmények adják Connes nemkommutatív geometriájának kiindulópontját. Az alapészrevétel talán úgy jellemezhető, hogy Descartes-nak a tér koordinátázására vonatkozó gondolatát Connes kiterjesztette „nemkommutatív koordináták” használatára.

A következőkben az előadó rámutatott, hogy Neumann János operátoralgebrai munkái nemcsak a geometria egy újfajta szemléletéhez vezettek hanem egy új kalkulushoz is. Nevezetesen, Connes a Newton által megfogalmazott infinitezimális változók fogalmát alapul véve bevezette a kvantumelméleti infinitezimális változókat (amelyek éppen az ún. kompakt operátorok), és kidolgozott egy kapcsolódó operátorelméleti integrálfogalmat (megemlítette annak érdekes tulajdonságai közül azt, hogy az integrál független az integrálban szereplő infinitezimálistól). Ezzel összefüggésben az előadás utolsó részében az előadó beszélt azon munkáiról, amelyekben a Riemann-geometriai távolság alapvető fogalmát kvantumos, operátoralgebrai környezetre terjesztette ki és vázolta ennek fizikai hátterét.

A matematika és a fizika számos területét érintő előadását Alain Connes egy táblázattal zárta, amiben bemutatta, hogy a nemkommutatív geometria mára a matematika szerteágazó területeivel áll kapcsolatban.

A Rényi Intézetben lezajlott esemény után New Yorkban a Főkonzulátus épülete adott otthont november 8-án egy filmvetítéssel egybekötött megemlékezésnek, amelynek során Lax Péter magyar-amerikai matematikus (az Abel-díj 2005. évi kitüntetettje) megkapta a „Magyar Érdemrend parancsnoki keresztje a csillaggal” kitüntetést. (Erről a hírt a Rényi honlapján olvashatják.) 

Lax professzor idén töltötte be 97. életévét, a fia vette át nevében az elismerést. Beszédében felemlítette, hogy amikor Lax Péter 1941-ben, 15 évesen New Yorkba érkezett, Neumann János is tanácsokkal látta el a kiemelkedő tehetségű fiatal matematikust további tanulmányait illetően. November 9-én pedig a New York University egyik termében egész napos konferencia foglalkozott Neumann János szerteágazó munkásságával, annak későbbi hatásával, illetve olyan időszerű problémák megvitatásával, mint a mesterséges intelligencia térnyerése és ennek hatása a társadalomra.

A konferencián a Rényi Intézet képviseletében Stipsicz András osztotta meg a hallgatósággal a Jones-polinom felfedezésének történetét: a Neumann-algebrák elmélete vezette Vaughan Jones Új-Zélandi matematikust egy új csomóinvariáns felfedezésére. A Jones-polinom új kutatási területet, sokaságok és csomók „kvantum-invariánsainak” kifejlesztését indította el. Jones felfedezéséért 1990-ben Fields Érmet kapott; sőt, ugyanezen alkalommal Edward Witten elméleti fizikust a Jones-polinom kvantumtér-elmélettel való definíciójáért ugyanebben az elismerésben részesítették. A Jones-polinom története azonban itt nem ért véget, 2000-ben Mikhal Khovanov egy olyan homológiaelméletet talált, amelynek Euler-karakterisztikája a Jones-polinom, majd 2015-ben Lipshitz és Sarkar olyan tereket tudtak csomókhoz rendelni, amelyeknek szinguláris homológiája épp a Khovanov-homológia. Ilymódon Neumann János majd egy évszázada bevezetett algebrái napjaink matematikájára is inspiráló és megtermékenyítő hatással vannak, mutatva a Neumann-algebrák matematikában és fizikában elfoglalt központi szerepét.

Molnár Lajos, Szegedi Egyetem, Bolyai Intézet, Analízis Tanszék vezetője

Stipsicz András, Rényi Alfréd Matematikai Kutatóintézet igazgatója

2023. november 27-én a hollandiai Delfti Műszaki Egyetem adott otthon az Ember a jövőből – Neumann János maradandó öröksége című Neumann-szimpóziumnak. A szerk.