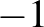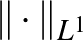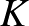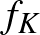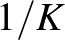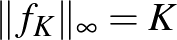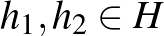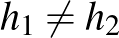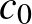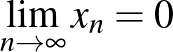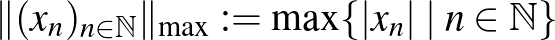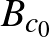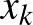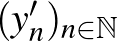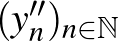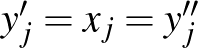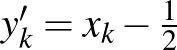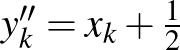Ebben a cikkben valós normált terekről és azok távolságtartó leképezéseiről lesz szó. A szükséges fogalmak bevezetése után ismertetünk egy nagyon szép tételt, a Mazur–Ulam-tételt, majd rátérünk annak egy nagyon természetes általánosítására (Mankiewicz tétele). Ezek után teszünk néhány megjegyzést arra vonatkozóan, hogy hogyan néz ki egy gömb és a felülete, és kimondjuk Tingley sejtését, ami amennyire egyszerűnek hangzik, annyira nehéz. (És a mai napig megoldatlan.)
1. Normált terek
Elsőként fel kell idéznünk, mik a valós vektorterek. A cikkben lévő állítások szemléltetéséhez elég lenne a valós síkra, azaz az  térre gondolni, és azt különböző struktúrákkal ellátni. De ahhoz, hogy az állításokat az eredeti formájukban mondjuk ki (rámutatva a nehézségekre), szükség van az absztrakt definíciókra, és néhány bonyolultabb példára. Azok, akik „csak a nagy képre kíváncsiak”, az alábbihoz hasonló szürke keretes bekezdéseket nyugodtan átugorhatják, és vektortér/normált tér helyett gondolhatnak
térre gondolni, és azt különböző struktúrákkal ellátni. De ahhoz, hogy az állításokat az eredeti formájukban mondjuk ki (rámutatva a nehézségekre), szükség van az absztrakt definíciókra, és néhány bonyolultabb példára. Azok, akik „csak a nagy képre kíváncsiak”, az alábbihoz hasonló szürke keretes bekezdéseket nyugodtan átugorhatják, és vektortér/normált tér helyett gondolhatnak 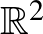 -re, és azokra a konkrét normákra, amiket említeni fogunk.
-re, és azokra a konkrét normákra, amiket említeni fogunk.
|
Valós vektortér alatt egy olyan 1) Asszociatív, azaz minden 2) Kommutatív, azaz minden 3) Létezik neutrális elem, azaz olyan 0-val jelölt elem, amelyre minden 4) Minden A skalárral való szorzásra vonatkozó zárójelezési szabályok pedig az alábbiak: 5) Minden 6) Minden 7) Minden 8) Minden Példák valós vektorterekre: Ahogy már említettük, a korábbról ismert |
Most bevezetjük a norma fogalmát, ami a hossznak egy természetes általánosítása. Mielőtt megadjuk a precíz definíciót, megemlítünk három konkrét példát az 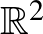 síkon. Ezekről az olvasó megpróbálhatja igazolni, hogy valóban teljesítik a lenti definícióban szereplő a)-b)-c) feltételeket. Egy
síkon. Ezekről az olvasó megpróbálhatja igazolni, hogy valóban teljesítik a lenti definícióban szereplő a)-b)-c) feltételeket. Egy 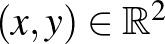 vektor normájára az
vektor normájára az  jelölést használjuk, ahol alsó indexben a
jelölést használjuk, ahol alsó indexben a 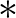 helyére írt jelekkel mondjuk meg, hogy a három ismertetett norma közül melyikre gondolunk. Nézzük tehát a három példát
helyére írt jelekkel mondjuk meg, hogy a három ismertetett norma közül melyikre gondolunk. Nézzük tehát a három példát  -en:
-en:
n1) 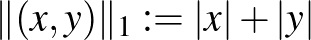 . Ha ebben a normában számoljuk ki például a
. Ha ebben a normában számoljuk ki például a 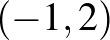 vektor hosszát, akkor azt kapjuk, hogy
vektor hosszát, akkor azt kapjuk, hogy 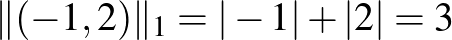 . Érdemes megfigyelni, hogy ez a hosszfogalom nem invariáns az origó körüli forgatásra. Ha a
. Érdemes megfigyelni, hogy ez a hosszfogalom nem invariáns az origó körüli forgatásra. Ha a 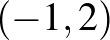 vektort beforgatjuk az
vektort beforgatjuk az  tengelyre, akkor a
tengelyre, akkor a  vektort kapjuk, aminek a hossza
vektort kapjuk, aminek a hossza  .
.
n2) 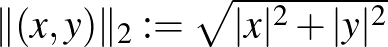 . Ebben a normában ugyanannak a
. Ebben a normában ugyanannak a 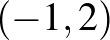 vektornak a hossza
vektornak a hossza  . Ez a középiskolából ismert euklideszi hosszfogalom.
. Ez a középiskolából ismert euklideszi hosszfogalom.
n3) 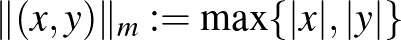 , azaz a két koordináta abszolútértéke közül a nagyobb. Ebben a normában a
, azaz a két koordináta abszolútértéke közül a nagyobb. Ebben a normában a 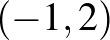 vektor hossza
vektor hossza 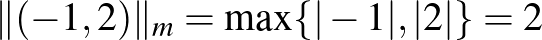 .
.
Általában, egy 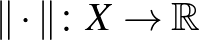 nemnegatív függvényt normának (vagy ha úgy tetszik: hosszfüggvénynek) nevezünk az
nemnegatív függvényt normának (vagy ha úgy tetszik: hosszfüggvénynek) nevezünk az 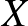 vektortéren, ha teljesíti az alábbi három tulajdonságot:
vektortéren, ha teljesíti az alábbi három tulajdonságot:
a)  , azaz a nulla vektor hossza 0, és csak a nulla vektornak 0 a hossza.
, azaz a nulla vektor hossza 0, és csak a nulla vektornak 0 a hossza.
b) Minden valós 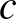 számra és
számra és 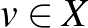 vektorra
vektorra 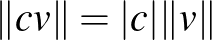 , azaz ha megnyújtunk egy vektort, és megmérjük a hosszát, akkor ugyanazt kapjuk, mintha először megmérnénk a hosszát, és vennénk a kapott szám
, azaz ha megnyújtunk egy vektort, és megmérjük a hosszát, akkor ugyanazt kapjuk, mintha először megmérnénk a hosszát, és vennénk a kapott szám  -szeresét.
-szeresét.
c) Minden 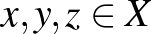 -re
-re  . Ez az úgynevezett háromszög-egyenlőtlenség.
. Ez az úgynevezett háromszög-egyenlőtlenség.
Mint az n1)-n2)-n3) példákban láttuk, ugyanazon az 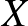 vektortéren több különböző normát is be lehet vezetni, ezért a félreértések elkerülése végett, ha
vektortéren több különböző normát is be lehet vezetni, ezért a félreértések elkerülése végett, ha 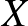 vektortérről mint normával ellátott térről akarunk beszélni, mindig feltüntetjük, hogy pontosan melyik normára gondolunk. Tehát ha a középiskolában megszokott módon akarunk hosszat számolni, akkor ezt úgy jelöljük, hogy
vektortérről mint normával ellátott térről akarunk beszélni, mindig feltüntetjük, hogy pontosan melyik normára gondolunk. Tehát ha a középiskolában megszokott módon akarunk hosszat számolni, akkor ezt úgy jelöljük, hogy 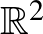 helyett
helyett 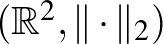 -t írunk. Egy
-t írunk. Egy 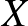 vektorteret a
vektorteret a  normával ellátva normált térnek hívunk, és
normával ellátva normált térnek hívunk, és 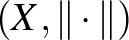 -val jelölünk.
-val jelölünk.
|
A normált tér fogalma az 1920-as években kristályosodott ki. Természetesen az emberek korábban is dolgoztak olyan struktúrákban (főleg függvényterekben), amikben volt hosszfüggvény, és többen is megfogalmaztak feltételrendszereket, amelyek az a)-b)-c) tulajdonságokra hasonlítanak, de a fenti axiomatikus bevezetés Stefan Banach 1932-es Théorie des opérations linéaires című könyvében jelent meg először. Ugyanitt jelent meg először a modern analízis egyik legfontosabb fogalma, a teljesség. Az
De nem találunk olyan |
2. A Mazur–Ulam-tétel és Mankiewicz tétele
Az előző szekcióban bevezettük a normált tér fogalmát. A norma segítségével beszélhetünk két vektor távolságáról is: egy 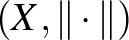 normált tér két
normált tér két 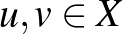 pontjának távolsága a különbségük hossza, azaz az
pontjának távolsága a különbségük hossza, azaz az 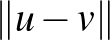 szám. Az a1)-a2)-a3) példákon szemléltetve az
szám. Az a1)-a2)-a3) példákon szemléltetve az 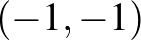 és
és 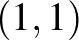 pontoknak a távolsága a különböző normákban:
pontoknak a távolsága a különböző normákban:  ,
,  , és
, és 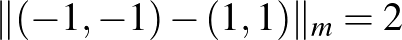 .
.
Tehát egy normált téren tudunk elemeket összeadni, tudunk számmal szorozni, tudunk hosszat mérni, és tudunk távolságot mérni. Vegyünk két normált teret, 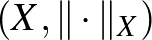 -et és
-et és 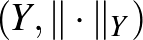 -t. Egy
-t. Egy 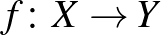 függvényt izometriának nevezünk, ha minden
függvényt izometriának nevezünk, ha minden 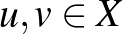 -re
-re 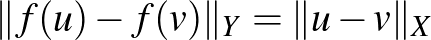 . Szavakkal elmondva,
. Szavakkal elmondva, 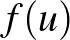 és
és 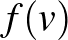 távolsága
távolsága 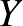 -ban ugyanannyi, mint az
-ban ugyanannyi, mint az 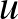 és
és 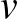 távolsága
távolsága 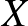 -ben, akárhogy is választjuk az
-ben, akárhogy is választjuk az 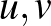 . Az egyszerűség kedvéért tegyük fel, hogy
. Az egyszerűség kedvéért tegyük fel, hogy 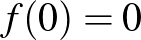 .
.
Felmerül a kérdés, hogy egy olyan függvény, ami megőrzi a távolságot, vajon megőrzi-e a lineáris struktúrát (azaz az összeadást és a számmal szorzást) is? Általában semmi okunk ebben reménykedni, hiszen a lineáris struktúra 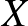 -en egy dolog, a hosszfogalom az
-en egy dolog, a hosszfogalom az 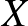 elemein pedig egy másik dolog. Stanisław Mazur és Stanisław Ulam gyönyörű tétele [7] azt mondja, hogy ha a szóban forgó izometria szürjektív, akkor mégis ez a helyzet!
elemein pedig egy másik dolog. Stanisław Mazur és Stanisław Ulam gyönyörű tétele [7] azt mondja, hogy ha a szóban forgó izometria szürjektív, akkor mégis ez a helyzet!
|
Mazur–Ulam-tétel (1932) Legyenek
Ekkor |
A Mazur–Ulam-tételre számtalan bizonyítás ismert, az egyik legszebb és legelemibb Jussi Väisälä bizonyítása [11]. A tételben feltettük, hogy 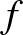 kölcsönösen egyértelmű. Azaz
kölcsönösen egyértelmű. Azaz 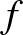 injektív (ha
injektív (ha 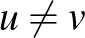 , akkor
, akkor 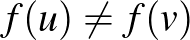 ) és
) és 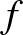 szürjektív (minden
szürjektív (minden 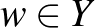 -hoz van olyan
-hoz van olyan 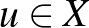 , amelyre
, amelyre 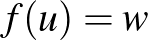 ). Mennyire fontosak ezek a feltételek? Az injektivitás automatikusan teljesül, hiszen ha
). Mennyire fontosak ezek a feltételek? Az injektivitás automatikusan teljesül, hiszen ha 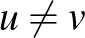 , akkor
, akkor 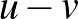 nem az
nem az 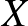 nullvektora, akkor viszont a norma a) tulajdonsága miatt
nullvektora, akkor viszont a norma a) tulajdonsága miatt 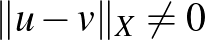 . Mivel
. Mivel 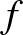 izometria, ezért
izometria, ezért 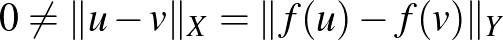 , így megint az a) tulajdonságot használva
, így megint az a) tulajdonságot használva 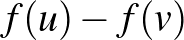 nem az
nem az  tér nullvektora, és így
tér nullvektora, és így 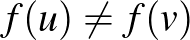 . Mit mondhatunk a szürjektivitásra vonatkozó feltevésről? Nem hagyható el? Az alábbi egyszerű példa azt mutatja, hogy nem.
. Mit mondhatunk a szürjektivitásra vonatkozó feltevésről? Nem hagyható el? Az alábbi egyszerű példa azt mutatja, hogy nem.
Ha 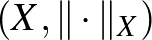 a számegyenes az abszolútértékkel,
a számegyenes az abszolútértékkel, 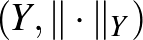 pedig az n3)-ban bevezetett tér, akkor az
pedig az n3)-ban bevezetett tér, akkor az 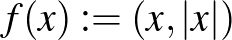 függvény egy izometria. Valóban, minden
függvény egy izometria. Valóban, minden  -re
-re
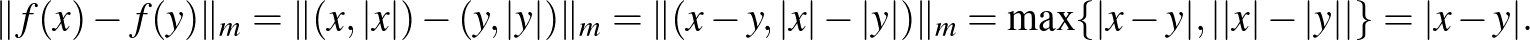
Az is teljesül, hogy az 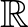 nullelemének képe az
nullelemének képe az 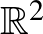 nulleleme:
nulleleme: 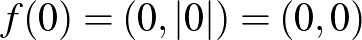 . De az nem igaz, hogy
. De az nem igaz, hogy 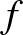 lineáris! Az
lineáris! Az 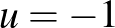 ,
, 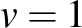 választással
választással  , míg
, míg 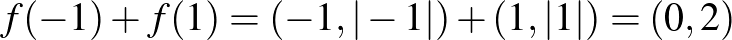 . Tehát
. Tehát 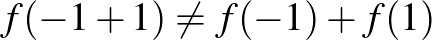 . Ez a példa valóban ellenpélda, de eléggé elfajult abban az értelemben, hogy az
. Ez a példa valóban ellenpélda, de eléggé elfajult abban az értelemben, hogy az 
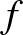 -általi képe
-általi képe 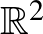 -ben az abszolútérték függvény grafikonja, ami egy nagyon sovány halmaz.
-ben az abszolútérték függvény grafikonja, ami egy nagyon sovány halmaz.
Piotr Mankiewicz megmutatta, hogy el lehet hagyni a szürjektivitást, ha feltesszük, hogy az izometria képe egy szép kövér halmaz [6]. Az egyszerűség kedvéért a tételt csak egy speciális esetben mondjuk ki. Elsőként fel kell idézzük a 0 körüli zárt egységgömb fogalmát: 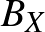 jelöli azon
jelöli azon 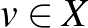 pontok halmazát, amelyeknek nullától vett távolsága legfeljebb
pontok halmazát, amelyeknek nullától vett távolsága legfeljebb  , azaz
, azaz 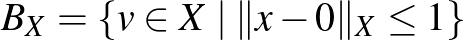 .
.
|
Mankiewicz tétel (1972) Legyenek |
3. Hogy néz ki egy gömb?
Mielőtt továbbmennénk, gondoljuk át, hogy mit mond az előző állítás. Először is jegyezzük meg, hogy egy bijektív lineáris izometria létezése 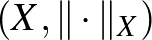 és
és 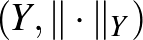 között azt mondja, hogy pusztán a metrikus és lineáris szerkezetük alapján nem tudjuk
között azt mondja, hogy pusztán a metrikus és lineáris szerkezetük alapján nem tudjuk 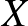 -et és
-et és 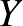 -t megkülönböztetni. Mankiewicz tétele azt mondja, hogy ha meg akarjuk tudni, hogy két tér megkülönböztethető-e, akkor elég ha megnézzük a gömbjeiket. De mit látunk, ha ránézünk egy normált tér gömbjére? Hogy néz ki egy gömb?
-t megkülönböztetni. Mankiewicz tétele azt mondja, hogy ha meg akarjuk tudni, hogy két tér megkülönböztethető-e, akkor elég ha megnézzük a gömbjeiket. De mit látunk, ha ránézünk egy normált tér gömbjére? Hogy néz ki egy gömb?
Kezdjünk megint az a1)-a2)-a3) példákkal. Az alábbi ábrán az 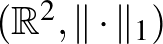 ,
, 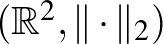 , és
, és 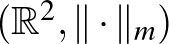 terek egységgömbjeit (vagy ha úgy tetszik, egységkörlapjait) látjuk egymás mellett.
terek egységgömbjeit (vagy ha úgy tetszik, egységkörlapjait) látjuk egymás mellett.

Rögtön látszik, hogy a két szélső gömb sok dologban különbözik a középen lévő „szokásos gömbtől”. A 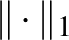 - és
- és 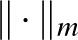 -gömböknek vannak csúcsai, ami elsőre szokatlannak hathat. Sőt, a gömb felülete tartalmaz szakaszokat. (Az
-gömböknek vannak csúcsai, ami elsőre szokatlannak hathat. Sőt, a gömb felülete tartalmaz szakaszokat. (Az 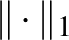 -gömb felülete tartalmazza például az
-gömb felülete tartalmazza például az 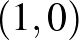 és
és 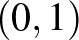 közti szakaszt, az
közti szakaszt, az 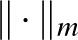 -gömb pedig tartalmazza például a
-gömb pedig tartalmazza például a 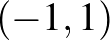 és
és 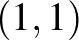 pontok közti szakaszt. Ennek van egy meglehetősen kellemetlen következménye. A
pontok közti szakaszt. Ennek van egy meglehetősen kellemetlen következménye. A 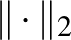 -norma esetén bármely két
-norma esetén bármely két 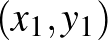 ,
, 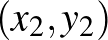 pont esetén egyetlen olyan
pont esetén egyetlen olyan 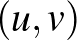 pont van, amelyik mindkettőtől
pont van, amelyik mindkettőtől 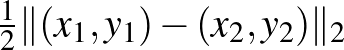 távolságra van, nevezetesen az őket összekötő szakasz felezőpontja,
távolságra van, nevezetesen az őket összekötő szakasz felezőpontja,  ). Ez amiatt van, hogy két pont köré rajzolt megfelelő sugarú gömb egyetlen pontban metszi egymást. Míg például a
). Ez amiatt van, hogy két pont köré rajzolt megfelelő sugarú gömb egyetlen pontban metszi egymást. Míg például a 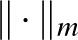 esetben a határon lévő szakaszok rengeteg ilyen pontot generálhatnak. Könnyen látszik, hogy
esetben a határon lévő szakaszok rengeteg ilyen pontot generálhatnak. Könnyen látszik, hogy 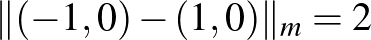 , és minden
, és minden ![$t\in[0,1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img135.png) -re
-re 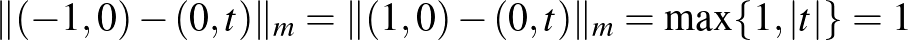 .
.
|
Már a fenti példák is mutatják, hogy normált terek gömbjei általában egzotikusabbak, mint a megszokott euklideszi gömb, tehát az ember nem hagyatkozhat az euklideszi szemléletére. Nézzünk még egy példát arra, hogy egy vektortéren két különböző norma gömbje mennyire eltérő lehet. A fent említett gömbök az
Ez is egy olyan tulajdonság, amit az ember csak véges dimenziós tereket ismerve természetesnek vesz. Azonban ez a tulajdonság végtelen dimenzióban általában nem teljesül. Térjünk vissza a |
4. A Tingley-sejtés
Mankiewicz tételét látva felmerül a kérdés, hogy nem elég-e az egységgömbök helyett csak az egységgömbök felületét megnézni, ha el akarjuk dönteni, hogy két normált tér megkülönböztethető-e. Jelöljük a továbbiakban 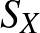 -szel az
-szel az 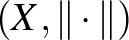 tér egységgömbjének felületét
tér egységgömbjének felületét
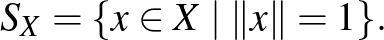
Tingley azt sejtette, hogy ha adott egy 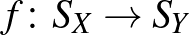 kölcsönösen egyértelmű izometria két normált tér gömbfelületei között, akkor azt mindig ki lehet terjeszteni
kölcsönösen egyértelmű izometria két normált tér gömbfelületei között, akkor azt mindig ki lehet terjeszteni 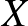 és
és 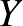 közötti szürjektív izometriává. (Tingley véges dimenziós normált terekkel foglalkozott, de a sejtés dimenziótól függetlenül érdekes.)
közötti szürjektív izometriává. (Tingley véges dimenziós normált terekkel foglalkozott, de a sejtés dimenziótól függetlenül érdekes.)
Ami az embernek rögtön eszébe jut, mint természetes kiterjesztés, az az alábbi:
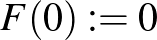 és
és 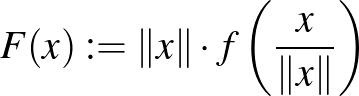 , ha
, ha 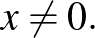
De mi garantálja, hogy ez a leképezés egy szürjektív izometria? Ne felejtsük el, hogy a Mazur–Ulam-tétel értelmében ennek az  kiterjesztésnek lineárisnak kéne lenni!
kiterjesztésnek lineárisnak kéne lenni!
Tingley az 1987-es [10] cikkében megmutatta, hogy a gömbfelület átellenes pontjai átellenes pontokba mennek, de már ennek a látszólag nyilvánvaló állításnak a bizonyítása is rendkívül bonyolult. Érdemes megjegyezni, hogy ennek az állításnak mély mondanivalója van. Nevezetesen, hogy az átellenességnek (ami egy algebrai tulajdonság, azt mondja, hogy az egyik pont a másik 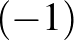 -szerese) van valami metrikus tartalma is. A síkon a
-szerese) van valami metrikus tartalma is. A síkon a 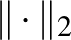 norma esetében nem nehéz meglátni a metrikus tartalmat. Az egységgömbön lévő pontok távolsága legfeljebb
norma esetében nem nehéz meglátni a metrikus tartalmat. Az egységgömbön lévő pontok távolsága legfeljebb  lehet, és
lehet, és 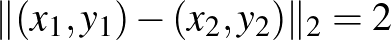 pontosan akkor, ha
pontosan akkor, ha 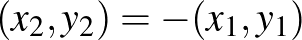 . De ugyanez az állítás a
. De ugyanez az állítás a 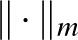 normára nem igaz. A gömb átmérője továbbra is
normára nem igaz. A gömb átmérője továbbra is  , de bármely
, de bármely 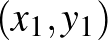 ponthoz végtelen sok olyan
ponthoz végtelen sok olyan 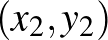 pont van, amire
pont van, amire 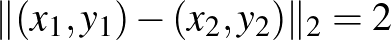 . (Emlékezzünk vissza, hogy a gömbfelület ebben az esetben egy négyzet, és annak bármely pontjától a szemközti oldal minden pontja
. (Emlékezzünk vissza, hogy a gömbfelület ebben az esetben egy négyzet, és annak bármely pontjától a szemközti oldal minden pontja  távolságra van a
távolságra van a 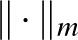 normából származtatott távolság szerint.)
normából származtatott távolság szerint.)
A nehézséget az okozza, hogy egy normált tér egységgömbjének felülete nagyon elvadult lehet, és általában, ha csak annyit mondanak, hogy van egy függvényünk két normált tér gömbfelülete között, akkor nincs mibe kapaszkodnunk. Ha a kérdést nem úgy tesszük fel, hogy tetszőleges 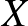 és
és 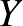 normált terekre igaz-e, hanem konkrétan meg is nevezzük a teret (vagy esetleg tereknek egy szép osztályát), akkor a kérdés egyszerűbbé válhat, mert a konkrét terek konkrét gömbfelületéről már lehetnek információink. Így például Kadets és Martín 2012-ben [5] bebizonyította Tingley sejtését olyan véges dimenziós terekre, ahol a gömb egy poliéder. Szintén igazolták a sejtést bizonyos függvényalgebrákra, operátoralgebrákra, és egyéb szép struktúrákra (lásd [3,2,4,8,9], a teljesség igénye nélkül.)
normált terekre igaz-e, hanem konkrétan meg is nevezzük a teret (vagy esetleg tereknek egy szép osztályát), akkor a kérdés egyszerűbbé válhat, mert a konkrét terek konkrét gömbfelületéről már lehetnek információink. Így például Kadets és Martín 2012-ben [5] bebizonyította Tingley sejtését olyan véges dimenziós terekre, ahol a gömb egy poliéder. Szintén igazolták a sejtést bizonyos függvényalgebrákra, operátoralgebrákra, és egyéb szép struktúrákra (lásd [3,2,4,8,9], a teljesség igénye nélkül.)
Az általános sejtés a mai napig nyitott, sőt, megdöbbentő módon még kétdimenziós terekre sem volt megválaszolva egeszen mostanáig. Taras Banakh az 2022-ben publikált [1] cikkében megmutatta, hogy Tingley sejtése igaz, ha a szóban forgó terek kétdimenziósak.
|
Érdemes megjegyezni, hogy ahogy Kadets és Martín, úgy Tingley is véges dimenziós normált tereket vizsgált. Az eredményeik erősen támaszkodnak arra, hogy a gömböknek bizonyos értelemben sok extremális pontja van. (Egy |
Daryl Tingley a University of New Brunswick nyugalmazott professzora. Fő kutatási területe a funkcionálanalízis, azon belül is Banach terek elmélete (geometriája). A nevéhez fűződő sejtés mellett érdemes néhány szót ejteni kertészeti sikereiről is: feleségével (aki szintén matematikus) Maureen Tingley-vel díjat díjra halmoznak óriástök növesztésben. Erről itt és itt lehet többet olvasni.

Tingley és felesége a neguaci óriástök fesztivál első díjával. (Fotó: Camille Breau)
Irodalomjegyzék
- [1] T. BANAKH, Every 2-dimensional Banach space has the Mazur–Ulam property, Linear Algebra and its Applications, 632 (2022), 268–280.
[2] M. CUETO-AVELLANEDA, A. M. PERALTA, The Mazur–Ulam property for commutative von Neumann algebras, Linear and Multilinear Algebra, 68 (2020), 337–362.
[3] F. J. FERNáNDEZ-POLO AND A.M.PERALTA, On the extension of isometries between the unit spheres of a 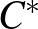 -algebra and
-algebra and 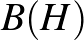 , Transactions of the American Mathematical Society, 5 (2018), 63–80.
, Transactions of the American Mathematical Society, 5 (2018), 63–80.
[4] O. HATORI, S. OI, R. S. TOGASHI, Tingley's problem on uniform algebras, Journal of Mathematical Analysis and Applications, 503 (2021), Paper No. 125346.
[5] V. KADETS, M. MARTíN, Extension of isometries between unit spheres of finite-dimensional polyhedral Banach spaces, Journal of Mathematical Analysis and Applications, 396 (2012), 441–447.
[6] P. MANKIEWICZ, On extension of isometries in normed linear spaces. Bulletin L'Académie Polonaise des Science, Série des Sciences Mathématiques, Astronomiques et Physiques 20 (1972), 367–371.
[7] S. MAZUR, S. ULAM, Sur les transformations isométriques d'espaces vectoriels normés, Comptes Rendus de l'Académie des Sciences, 194 (1932), 946–948.
[8] M. MORI, Tingley’s problem through the facial structure of operator algebras, Journal of Mathematical Analysis and Applications, 266 (2018), 1281–1298.
[9] A. M. PERALTA, A survey on Tingley’s problem for operator algebras, Acta Scientiarum Mathematicarum, 84 (2018), 81–123.
[10] D. TINGLEY, Isometries of the unit sphere, Geometriae Dedicata, 22 (1987), 371–378.
[11] J. VäISäLä A Proof of the Mazur-Ulam Theorem, The American Mathematical Monthly, 110 (2003), 633–635.
Titkos Tamás
Rényi Alfréd Matematikai Kutatóintézet, Budapesti Gazdasági Egyetem










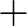
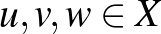
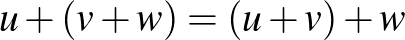
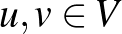
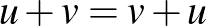
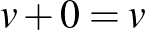
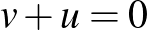
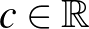
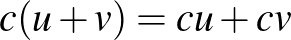
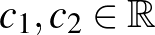

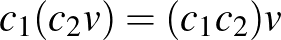
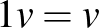
![$[0,1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img23.png)
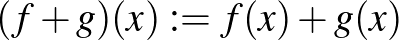
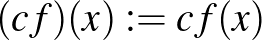
![$F[0,1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img26.png)
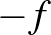
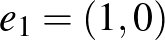

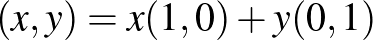
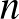
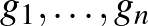
![$f\in F[0,1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img34.png)
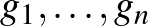
![$C[0,1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img36.png)
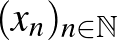
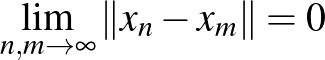
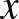
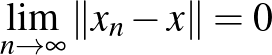
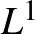

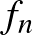
![$[0,\frac{1}{2}-\frac{1}{n}]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img67.png)
![$[\frac{1}{2}+\frac{1}{n},1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img69.png)
![$[1/2-1/n,1/2+1/n]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img70.png)
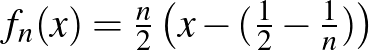
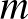
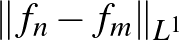

![$f\in C[0,1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img74.png)
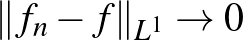
![$[0,1/2]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img76.png)
![$[1/2,1]$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img77.png)
![$\Vert f\Vert _{\infty}=\max\{\vert f(x)\vert\mid x\in[0,1]\}$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img79.png)

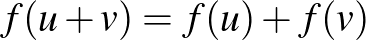
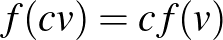
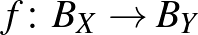
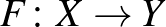

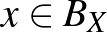


![$\max\{\vert f(x)\vert\mid x\in[0,1]\leq 1\}$](/images/stories/latexuj/2022-12/2022-12-atingleysejtes/img138.png)