Az index tanítása nemzetközi környezetben

Az index bevezetése nemzetközi környezetben mérnök hallgatók részére – szubjektív beszámoló

A környezet

2007-től kezdődően Ciprus szigetén, Famaguszta városában a Kelet-Mediterrán Egyetem Ipari Mérnök Tanszékén (Department of Industrial Engineering, Eastern Mediterranean University) tanítottam hallgatókat mindhárom szinten. Famaguszta a kettéosztott sziget északi, azaz török részén található. Az egyetemet 1979-ben alapították, és ez az egész sziget első egyeteme. Az alapítás ötletét a török felsőoktatás egy sajátossága adta. A három részre osztott középiskola elvégzése után az egyetemekre jelentkező fiataloknak egységes felvételi vizsgát kell letenniük. Az illetékes hivatal sorrendbe állítja őket. Az egyetemek kötelesek a hozzájuk jelentkezőket ebben a sorrendben felvenni. Egy személy a sorrendjüket megjelölve több helyre is jelentkezhet. Az első olyan helyre veszik fel, ahova a jelentkezők sorrendje szerint befér. Mint minden vizsga esetében, itt is lehetséges, hogy valakinek jó vagy éppen ellenkezőleg rossz napja van. Az utóbbiak között értékes emberek is lehetnek, akiket kár volna kirekeszteni a felsőoktatásból. Ha azonban Ciprusra jönnek, ami formálisan másik országnak számít, akkor tanulmányaik sikeres befejezése után egy egyszerű honosítási eljárás után diplomájukat Törökországban is hasznosíthatják. Az egyetem egyben a ciprusi török közösség számára is hasznos, mert ők helyben tanulhatnak.

Törökországban az egyetemi oktatás nyelve hagyományosan az angol volt. Ez a mai Boszporusz Egyetem (Boğaziçi University) történetéből adódik, aminek elődjét a 19. század első felében alapították, és ami mindvégig angol nyelven működött, még az 1971-es államosítás után is. Emiatt Cipruson is angol lett a tanítás nyelve. Ez viszont lehetőséget adott arra, hogy a török nyelvi környezeten kívülről is vonzzon hallgatókat, ami meg is történt. Bár a törökországi hallgatók csoportja a legnagyobb, mára már mintegy 100 országból érkeznek diákok. Én tanítottam hallgatókat Kirgiziától Marokkóig és Bulgáriától Zambiáig. Mára a nigériaiak száma is meglehetősen magas, de sokan jönnek az arab országokból. Még Szaúd-Arábiából is vannak, egykori menekültek leszármazottai, akik ma is menekültnek számítanak. Közöttük több lány is. Az alábbiakban a kulturális háttér jelzésére említem a vallásokat is. Vallási ellentétek azonban nincsenek a hallgatók között. A különböző kultúrák békésen élnek egymás mellett. Mindazonáltal megjegyzendő, hogy az egyetem területén mecset is és keresztény templom is van. Az utóbbit több felekezet is használja.

Felmerül a probléma

Az ipari mérnök név nem adja vissza jól a szakma lényegét, amit a magam részéről a szervező mérnök kifejezéssel szoktam elmagyarázni. Tehát olyan ipari környezetben dolgozó szakemberről van szó, aki minden mérnöki szakmával jól együtt tud működni, az ott zajló folyamatokat szervezni képes. Az ipari mérnök szakma igen nagy átfedést mutat a vezetéstudománnyal és az operációkutatással.

Az ipari mérnök szakmában sok olyan probléma létezik, ahol számos, némileg különböző, de hasonló természetű dolog, például gyártmány, alkatrész, gép van, és ezeket kell valahogy elrendezni. A kérdés matematikai elemzése során ezeket az objektumokat az indexükkel nevezzük meg, és különböző paramétereik értékét részben a paraméter nevével, például hossz, illetve ezen név valamilyen rövid megnevezésével, például az adott esetben 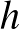$h$ , és az adott objektum indexével azonosítjuk, például 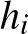$h_{i}$ . Az index tehát semmi más, mint az adott objektum neve, igaz, elég absztrakt formában megadva. Ebben az sem zavar, hogy különböző természetű objektumok rendelkezhetnek látszólag azonos indexszel, például beszélhetünk 1 indexű (azaz 1-es) gépről is és 1 indexű (azaz 1-es) munkadarabról is, mert ezeket eltérő természetük miatt nem fogjuk összekeverni. Ha két vagy több objektum közötti kapcsolatot akarunk kifejezni, akkor kettős vagy többes indexezést használunk, felsorolva mindazon objektumokat, amelyek a kapcsolatban benne vannak. Például, ha azt kell eldönteni, hogy az 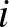$i$ munkadarab megmunkálása után közvetlenül a 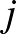$j$ munkadarab megmunkálása következik-e, akkor ennek az igen/nem kérdés eredményének leírására bevezethetjük az 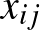$x_{ij}$ változót. (Bővebb magyarázat alább, az utazó ügynök feladatánál található.)

Az index használata már a legelső szakmai tárgyakban előjön, és tipikus a termelés irányításával kapcsolatos témákban.

Egy ízben egy zambiai hallgatónő jött konzultációra egy másik diákkal. A feltett kérdést próbáltam legjobb tudásom szerint megfelelni, de válaszom használhatatlan volt számukra. Egy ideig reménytelenül körbe-körbe jártunk, majd a zambiai lány valahogy megváltoztatta a kérdést, amiből rájöttem, hogy nem az előadott számítási módszert nem értik, hanem az index fogalmát. Ettől kezdve sínen voltunk, és a megbeszélés sikeresen zárult.

Megkaptam azonban a leckét, ezentúl az index mibenlétét mindig el kell magyaráznom.

Első kísérlet: évek

Azt gondoltam, hogy ha olyan dolgokra hivatkozom, amelyeknek a neve szinte kivétel nélkül szám, akkor egyszerű dolgom lesz. Ilyenek az évek, amelyeket számokkal azonosítunk a nyugati kultúrában is és az iszlám (muszlim) kultúrában is. Ennek az a jelentősége, hogy a hallgatók többsége muszlim hitű volt, bár keresztények is érkeztek, főleg Afrikából.

Az évek között azért van kivétel, olyan, amelyiknek külön neve van. Magyarázatomat erre próbáltam építeni. Az iszlám kultúrában 570 neve az Elefánt éve. Azért ez, mert ekkor egy afrikai csapat megtámadta Mekkát. Nekik volt egy elefántjuk. Az év igazi jelentősége azonban az, hogy ez egyben Mohammed Próféta születésének éve is.

Feltettem tehát a kérdést az osztályban:

– Melyik az Elefánt éve?

Azt vártam, hogy kezek erdeje emelkedik a magasba, vagy számosan bekiabálják a választ. Nos, a kérdést néma csönd követte. Ebből pedig nehéz volt tovább építkezni.

Második kísérlet: absztrakt rövidítések

Tanteremben csak kisebb példákat mutatunk be, hiszen a nagyobb feladatok átláthatatlanok volnának a hallgatóknak. Ha mondjuk csak öt gyártmányról van szó, akkor azoknak nyugodtan lehet nevet adni, például AIX5, AIX7, Z23, NGK, Y48L. Soha nem mondtam ki, de a két AIX-szel azt akartam sugallani, hogy nagyon hasonló dolgokról van szó, csak méretbeli különbség létezik közöttük. Ezeknek az absztrakt neveknek a használatával nem is volt semmi baj. Ugyanis mindenki látott ehhez hasonlókat a való életben. De ezekről átugrani az egyszerű számokra mint indexekre, túl nagy lépés volt. Bár az absztrakt neveket továbbra is használtam, de világossá vált, hogy az index fogalmának magyarázatára más módszert kell találnom.

Kitérő: az utazóügynök-feladat

Az optimalizálás elméletében több feladatnak is külön neve van, amely név valamely történethez, matematikai megfogalmazáshoz kötődik. Érdekes módon az utazó ügynök feladata pont arról szól, mint amit a neve mutat. Először 1832-ben merült fel egy német nyelvű, utazó kereskedőknek tanácsokat adó kézikönyvben. A kereskedő előre tudja, hogy mely városokat akarja felkeresni. Ezek között kell egy körutat megtennie úgy, hogy annak végén visszaérjen a saját városába, amely kiindulásul szolgált. A könyv tanácsa szerint úgy kell útját megszerveznie, hogy annak teljes hossza a lehető legkisebb legyen.

Ha a városokat és azok távolságát szimbólumként fogjuk fel, akkor ennek a feladatnak az ipari mérnöki szakma számos, egymástól távoli területén van alkalmazása. Az egyik legtermészetesebb, hogy egy teherautó egy központi raktárból látja el bizonyos áruval a boltokat. Milyen sorrendben keresse fel az üzleteket, hogy útja a leggazdaságosabb legyen? Ha egy robot egy felületen több megmunkálást is végez meghatározott helyeken, például lyukat fúr vagy nyomtatott áramkörön alkatrészt forraszt, akkor mi legyen a megmunkálások sorrendje, hogy a robot útja a megmunkálások között, ami tulajdonképpen szükségeses de veszteséges idő, a lehető legrövidebb legyen?

Érdekes módon a feladatot matematikailag megfogalmazni csak sokára sikerült. Nevezetesen ismertté válása után csak 122 két évvel, 1954-ben született meg az első teljes modell Dantzig, Fulkerson és Johnson jóvoltából [1]. Az idők folyamán a feladatnak további modelljeit találták meg [2]. Az első modellt a szerzők nevének kezdőbetűi alapján szokás DFJ-modellnek is nevezni. Gyakorlati szempontból máig ez az egyik leghatékonyabb modell. Versenytársa a Miller–Tucker–Zemlin, azaz MTZ-modell [3]. Érdekes módon a két modell változói részben közösek. A DFJ-modell csak ezeket használja, az MTZ-modell másokat is. Most nem tárgyalom a teljes modelleket, hanem csak ezeket a közös változókat, amelyek az index tanításában szerepet játszottak.

A körút megtervezésének egyik legegyszerűbb módja, ha megadjuk, hogy a városok milyen sorrendben követik egymást. A legjobb sorrend persze számítás eredménye, azt az esetek többségében nem lehet előre tudni. A sorrend úgy is felfogható, hogy megmondjuk minden város esetében a változókat. Legyen

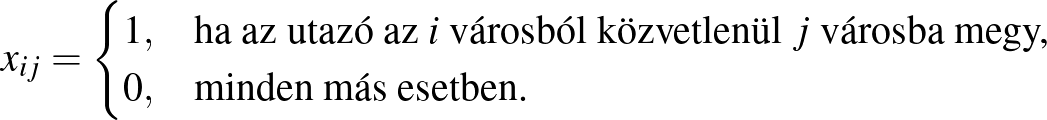
$\displaystyle x_{ij}=\begin{cases} 1,&\text{ha az utazó az } i \text{ városb... ...} j \text{ városba megy,}\\ 0,&\text{minden más esetben.}\\ \end{cases}$

A változók használatának módja az, hogy velük le lehet írni a körút szerkezetének fontos két tulajdonságát, amelyek egy párt alkotnak: (i) minden városból el kell utazni és (ii) minden városba meg kell érkezni. E két feltétel matematikai megfogalmazásához érdemes átfogalmazni az 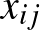$x_{ij}$ változó jelentését:

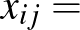$x_{ij}=$ hányszor megy az utazó 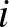$i$ városból 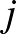$j$ -be = hányszor érkezik meg az utazó 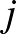$j$ városba 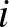$i$ városból.

Ha rögzített 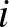$i$ város esetén az 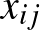$x_{ij}$ értékeket összegezzük, megkapjuk, hogy összesen hányszor ment tovább az 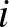$i$ városból. Körút esetén ennek 1-nek kell lennie. Hasonlóképp, rögzített 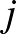$j$ város mellett az összeg azt adja meg, hogy hányszor érkezett meg az utazó a 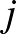$j$ városba. Így jutunk a két legnevezetesebb feltétel-csoporthoz [4]:

$\forall i\colon \sum\limits_{j\ne i} x_{ij}=1,\qquad \forall j\colon \sum\limits_{i\ne j} x_{ij}=1.$

Az utazóügynök-feladattal kapcsolatban annyit érdemes megjegyezni, hogy a most tárgyalt feltételek nem elegendőek. Ugyanis megengedik olyan „megoldás” előállítását is, amelyik nem egyetlen teljes körút, hanem több kisebb körútból áll [5]. A feladat matematikai modellezésének pont ez a nehézsége, hogy a kis köröket hogyan zárjuk ki.

Harmadik kísérlet: a megoldás

Segítségül híva az utazóügynök-feladatot, már a változók bevezetésénél kezdődött az index fogalmának tárgyalása. Mivel a problémát az absztrakt gondolkodási képesség hiányossága okozta, aminek oka annak az oktatási kultúrának a hiányossága lehet, ahonnan érkeztek, célszerűnek látszott konkrét példával indítani. A hallgatóság összetétele miatt törökországi példát választottam. Tegyük tehát fel, hogy Ankara, Isztambul, Izmir, Konya és Antalya városok között akarunk körutat szervezni. A változó bevezetése így kezdődik:

$\displaystyle x_{\text{Ankara},\text{Isztambul}}=\begin{cases} 1,&\text{ha az ... ...vetlenül Isztambulba megy,} \\ 0,&\text{minden más esetben.} \end{cases}$

Ez a konkrét példa érthető. Itt el lehet magyarázni, hogy információként az „Ankara” és „Isztambul” szavak túl hosszúk és lehet őket számokkal helyettesíteni, ami sok memóriát takarít meg. A dolog lényege, hogy csinálunk egy táblázatot – matematikai értelemben egy (kicsi) függvényt –, ami megmondja, hogy melyik várost melyik szám reprezentálja. Például így:

város	szám
Ankara	1
Isztambul	2
Izmir	3
Konya	4
Antalya	5

Természetesen az első, ismétlő kérdés, hogy mi 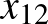$x_{12}$ , a válasz pedig 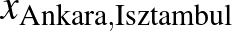$x_{\text{Ankara},\text{Isztambul}}$ . Ezt követően, még a fent tárgyalt matematikai feltételek bevezetése előtt, ellenőrző kérdéseket lehet feltenni. Például mi 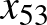$x_{53}$ ? A válasz 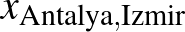$x_{\text{Antalya},\text{Izmir}}$ . Ezt követően már nem volt gond az index használatával.

Vizvári Béla
Eastern Mediterranean University

Hivatkozások

: [1] Dantzig, G. B., Fulkerson, D. R., Johnson, S. M., Solution of a large-scale traveling salesman problem, Operations Research, 2(1954), 393–410.

[2] Vizvári Béla Operációkutatási modellek, Typotex, 2009, Budapest. Összesen hat modellt tárgyal, de vannak továbbiak is.

[3] Miller, C. E., Tucker, A. W., Zemlin, R. A., Integer programming formulation of traveling salesman problem, J. of ACM, 3(1960), 326–329.

[4] Ezek a feltételek az úgynevezett hozzárendelési feladatban is szerepelnek, de azt most nem tárgyaljuk.

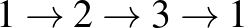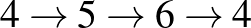[5] Például hat város esetén $1\to 2\to 3\to 1$ és $4\to 5\to 6\to 4$ két kis körút, mindegyik három utazásból áll. Minden városból továbbmegy az utazó, minden városba megérkezik, mégsem egyetlen körútról van szó.