Milyen módon léteznek a matematika objektumai, például a számok, a halmazok és a függvények? Csak az elménkben léteznek, mint például egy regény szereplői, vagy a gondolkodástól és a nyelvtől független létezők, mint például a bolygók és az elektronok? Igazak-e a matematika állításai (például, a Pitagorasz-tétel vagy a Farkas-lemma) attól függetlenül, hogy bárki elgondolná őket, vagy esetleg a matematika csak egy szimbólumokkal való formális játék? Ilyen típusú kérdésekkel a matematikafilozófia foglalkozik, amely a tudományfilozófia egy különösen fontos ága. A jelen tanulmány célja a matematikai állításokra vonatkozó antirealista elméletek – amelyek tagadják az elménktől független matematikai igazságok létezését – vázlatos történeti áttekintése, főleg a matematikai intuicionizmus és a konstruktivizmus irányzatokra koncentrálva.
Michael Dummett (1925–2011) nyomán matematikai realistának (vagy platonistának, idealistának) hívjuk azon szemantikai álláspontokat, amelyek szerint a matematikai állítások kapcsolatban vannak egy tudásunktól függetlenül létező valósággal, oly módon, hogy ez a valóság igazzá vagy hamissá teszi ezeket az állításokat, függetlenül attól, hogy ismerjük-e vagy egyáltalán képesek vagyunk-e megismerni ezeket az igazságértékeket [3]. Tehát a realista álláspont szerint a matematikai tételek igazságértéke nem függ a megismerő elmétől, a matematikus csupán felfedezi ezen igazságokat és nem megalkotja őket. Jól szemlélteti a matematika realista felfogását Charles Hermite (1822–1901) kijelentése: „Véleményem szerint a számok és az analízis függvényei nem elménk önkényes termékei. Hitem szerint rajtunk kívüli létezésük pontosan annyira szükségszerű, mint az objektív valóság tárgyaié. Éppúgy kutatunk utánuk és fedezzük fel őket, mint a fizikusok, a kémikusok és a zoológusok.” Dummett szerint [3] a realizmus elfogadása maga után vonja a kétértékűség (bivaliancia) elvének elfogadását, nevezetesen azt, hogy minden az adott osztályba tartozó állítás határozottan igaz vagy hamis (ettől az állítás még lehet eldönthetetlen egy adott formális-axiomatikus elméletben, azaz se nem bizonyítható, se nem cáfolható).
Ezzel szemben az antirealisták – például az intuicionisták, illetve a konstruktivisták – szerint nem létezik egy a tudásunktól független valóság, amely igazzá vagy hamissá tenné a matematikai állításokat és a matematikai objektumok csak az elménk konstrukciói. Ebből kifolyólag az antirealisták tagadják a kizárt harmadik elvének (tertium non datur; azaz minden 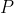 jólformált formulára vagy
jólformált formulára vagy 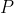 vagy
vagy 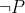 teljesül) érvényességét és új alapokra kívánják helyezni a matematikát a nemklasszikus (konstruktív) logikai konstansok1 bevezetésével.
teljesül) érvényességét és új alapokra kívánják helyezni a matematikát a nemklasszikus (konstruktív) logikai konstansok1 bevezetésével.
A logikai konstansoknak egy standard konstruktív értelmezése az ún. „bizonyítás” vagy „BHK” (Brouwer, Heyting, Kolmogorov) interpretáció [13]. Andrej Nyikolajevics Kolmogorov (1903–1987) a következőképpen definiálta a konstruktív logikai konstansok jelentését: az 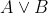 bizonyításához vagy
bizonyításához vagy 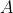 vagy
vagy 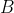 bizonyítását kell megadnunk. Az
bizonyítását kell megadnunk. Az 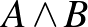 formula bizonyítást nyer, ha megadjuk
formula bizonyítást nyer, ha megadjuk 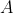 egy bizonyítását és
egy bizonyítását és 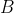 egy bizonyítását. Az
egy bizonyítását. Az 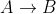 egy olyan konstrukció, amely segítségével
egy olyan konstrukció, amely segítségével 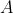 bármely bizonyítását
bármely bizonyítását 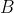 egy bizonyításává alakíthatjuk. A
egy bizonyításává alakíthatjuk. A 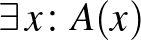 bizonyítása két részből áll: egy
bizonyítása két részből áll: egy 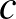 objektum konstrukciójából és
objektum konstrukciójából és 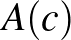 bizonyításából. A
bizonyításából. A 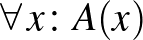 bizonyítása egy olyan eljárás, amely egy tetszőleges
bizonyítása egy olyan eljárás, amely egy tetszőleges 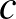 objektum konstrukciója alapján megkonstruálja
objektum konstrukciója alapján megkonstruálja 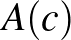 egy bizonyítását. Végül, az ellentmondásnak (
egy bizonyítását. Végül, az ellentmondásnak (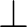 ) nincs bizonyítása, és a
) nincs bizonyítása, és a 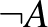 bizonyítása egy olyan konstrukció, amely
bizonyítása egy olyan konstrukció, amely 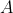 egy tetszőleges (feltételezett) bizonyításából egy ellentmondás (például
egy tetszőleges (feltételezett) bizonyításából egy ellentmondás (például 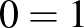 ) bizonyítását állítja elő. A „létezik” (
) bizonyítását állítja elő. A „létezik” (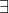 ) kvantor jelentésének azonosítása a „tudunk konstruálni”-val vezetett el ahhoz, hogy az intuicionista, illetve konstruktivista matematikusok csak a konstruktív egzisztenciális bizonyításokat fogadják el érvényesnek (az indirekt bizonyításokat nem).
) kvantor jelentésének azonosítása a „tudunk konstruálni”-val vezetett el ahhoz, hogy az intuicionista, illetve konstruktivista matematikusok csak a konstruktív egzisztenciális bizonyításokat fogadják el érvényesnek (az indirekt bizonyításokat nem).
Egy gyakran idézett példa nemkonstruktív matematikai bizonyításra a következő állításra adható: létezik két olyan 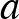 ,
, 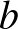 irracionális szám, amelyekkel
irracionális szám, amelyekkel 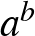 racionális. A Dummett által adott ügyes nemkonstruktív bizonyítás [2] így szól: legyen
racionális. A Dummett által adott ügyes nemkonstruktív bizonyítás [2] így szól: legyen 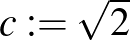 , ekkor a kizárt harmadik elvéből következik, hogy vagy
, ekkor a kizárt harmadik elvéből következik, hogy vagy 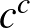 racionális vagy
racionális vagy 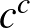 irraconális. (1) ha
irraconális. (1) ha 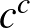 racionális akkor
racionális akkor 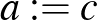 ,
, 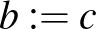 jó választás, (2) ha
jó választás, (2) ha 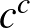 irracionális, akkor
irracionális, akkor 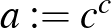 ,
, 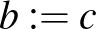 egy megfelelő választás a keresett számokra. Vegyük észre, hogy ez a bizonyítás (mivel a kizárt harmadik elvét használtuk) nem adja meg számunkra, hogy melyik a két keresett irracionális szám, tehát nem konstruktív. Természetesen nem az intuicionista logikai konstansok elfogadása jelenti a különbséget a realista és az antirealista álláspontok között. Egy realista is értékelheti, ha egy bizonyítás konstruktív – mivel az több információval szolgál a számára – és bevezethet jelöléseket a konstruktív „létezik” vagy a konstruktív „vagy” jelölésére. A fő különbség a nemklasszikus logikai konstansok használatának kizárólagos elfogadásában áll: azon álláspont elfogadásában, hogy csak és kizárólag ezek az elfogadható eszközök a matematikában. Noha többféle antirealista elmélet lehetséges és az intuicionista, illetve konstruktivista álláspontok nem egyformák (például az elsősorban Brouwer és Heyting nevéhez köthető intuicionizmus nem teljesen egyezik meg Bishop konstruktivizmusával vagy Markov konstruktív rekurzív matematikájával), azonban közel állnak egymáshoz, így együtt tárgyaljuk őket ebben a tanulmányban.
egy megfelelő választás a keresett számokra. Vegyük észre, hogy ez a bizonyítás (mivel a kizárt harmadik elvét használtuk) nem adja meg számunkra, hogy melyik a két keresett irracionális szám, tehát nem konstruktív. Természetesen nem az intuicionista logikai konstansok elfogadása jelenti a különbséget a realista és az antirealista álláspontok között. Egy realista is értékelheti, ha egy bizonyítás konstruktív – mivel az több információval szolgál a számára – és bevezethet jelöléseket a konstruktív „létezik” vagy a konstruktív „vagy” jelölésére. A fő különbség a nemklasszikus logikai konstansok használatának kizárólagos elfogadásában áll: azon álláspont elfogadásában, hogy csak és kizárólag ezek az elfogadható eszközök a matematikában. Noha többféle antirealista elmélet lehetséges és az intuicionista, illetve konstruktivista álláspontok nem egyformák (például az elsősorban Brouwer és Heyting nevéhez köthető intuicionizmus nem teljesen egyezik meg Bishop konstruktivizmusával vagy Markov konstruktív rekurzív matematikájával), azonban közel állnak egymáshoz, így együtt tárgyaljuk őket ebben a tanulmányban.
A realizmusnak több kritikusa akadt már a XIX. század folyamán. Talán a legismertebb közülük Leopold Kronecker (1823–1891) akit a konstruktivizmus vagy még inkább a finitizmus előfutárának is tekinthetünk [12]. Sokat elárul intuicionizmushoz közel álló nézeteiről gyakran idézett mondása: „a természetes számokat Isten teremtette, minden más emberi alkotás” (Heinrich Weber gyászbeszédéből). Kronecker körvonalazott egy „aritmetizálási” tervet, ami az algebra és az analízis számokkal való megalapozására vonatkozott. Csak azokat a definíciókat tekintette elfogadhatónak, amelyeket véges lépésben ellenőrizni lehet. Ezen elméletei vezették el a „tiszta” egzisztenciális bizonyítások kritikájához.
Fontos állomást jelentettek az antirealista matematika kialakulásában a francia preintuicionisták, akik például a Zermelo–Fraenkel-féle halmazelméletet megalapozó axiómarendszer kiválasztási axiómájának kritikája kapcsán fejtettek ki többé-kevésbé konstruktivista nézeteket. A legfontosabb alakjai ezen irányvonalnak [12]: Baire, Borel, Lebesgue, Lusin és Poincaré. Julius Henri Poincaré (1854–1912) támadta a Cantor-féle halmazelméletet (például az aktuális végtelen fogalmát) és a „logicizmust”. Logikai szkepticizmusát jellemzi mondása, miszerint: „egy szillogizmus nem tud semmilyen esszenciálisan újat tanítani nekünk” (1902). Amellett érvelt, hogy a matematikában többre van szükségünk mint logikára: intuíciókra. Szigorúan véve nem volt intuicionista, de kritikája a logikával kapcsolatban (például a teljes indukcióra vonatkozóan) a konstruktivizmus egyik elődjévé teszi. Emile Borel (1871–1956) nézetei közel álltak Kroneckeréihez, például úgy gondolta, hogy csak az effektíven (például, véges sok szóval) definiált objektumok léteznek a tudományban és a konzisztencia nem elégséges a létezéshez.
Luitzen Egbertus Jan Brouwer (1881–1966) holland matematikus nevéhez fűződik az intuicionizmus első precíz megfogalmazása, akinek filozófiájára Kant és Schopenhauer volt a legnagyobb hatással. Első ízben 1907-ben Amszterdamban a matematika megalapozásáról szóló doktori disszertációjában fejtette ki antirealista nézeteit. Brouwer szerint a matematika az elme belső szabad alkotása és független mindenféle nyelvtől vagy platonikus valóságtól. Szerinte a matematika nem függ a logikától és a logika a matematika része, valamint a matematikát nem lehet axiomatikus módon megalapozni. Brouwer elutasította a Hilbert-féle formalizmust és a Cantor-féle halmazelméletet. A logika számára csak egy megbízhatatlan eszköz a kommunikációra. A matematikai gondolkodás – Brouwer szerint – matematikai struktúrák megalkotásából áll, és a szillogizmusokhoz hasonló logikai struktúrák megjelenését csak a szabály alkalmazása közben végzett matematikai konstrukció igazolja. A logikát alkalmazott matematikának tekintette és empirikus tudománynak [12]. Szerinte nem létezik meghatározott matematikai igazság a gondolkodáson kívül, és egy állítás csak akkor lesz igaz, ha a szubjektum megtapasztalta az igazságát (amit a megfelelő mentális konstrukció véghezvitelével tud megtenni). Hasonlóképpen, egy állítás csak akkor lesz hamis, ha a szubjektum megtapasztalta a hamisságát (mivel felismerte, hogy egy meghatározott logikai konstrukció nem lehetséges). Tehát Brouwer szerint nincsenek nem megtapasztalt (tudásunktól független) igazságok. Ezen nézetei az intuicionista matematika megalkotásához vezettek, valamint a klasszikus (realista) matematika egy jelentős részének elutasításához [13]. Azonban Brouwer nemcsak negatív módon járult hozzá az intuicionista matematikához, nemcsak azzal, hogy bírált és elutasított néhány általa meg nem felelőnek tartott klasszikus matematikai módszert. Nevéhez fűződik a kiválasztási sorozatok fogalmának kidolgozása. Ezen sorozatok kulcsszerepet játszanak az intuicionista szám- és függvényfogalomban. Ezek a sorozatok vezették el Brouwert az egyenletes folytonosság tételének kimondásához, amely szerint – az intuicionista matematikában – minden korlátos, zárt intervallumot a valós számokba képező függvény egyenletesen folytonos.
Az első formális intuicionista rendszereket Brouwer tanítványa Arend Heyting (1898–1980) dolgozta ki. Az eredményként előálló intuicionista logikával technikai szempontból nincs probléma: definiálható intuicionista formális propozicionális- és predikátumkalkulus (amelyekben nem szerepel a kizárt harmadik elve) és az intuicionista predikátumlogikához adható interpretáció, például a Kripke-féle lehetséges világ szemantika, amelyre nézve az helyes és teljes. Egy alapvető eredmény az intuicionista logikával kapcsolatban, hogy a klasszikus és az intuicionista (propozicionális- és predikátum-) logika ekvikonzisztens. A propozicionális logikára ezt először Glivenko bizonyította be 1929-ben. Megmutatta, hogy egy 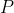 formula akkor és csak akkor vezethető le a klasszikus propozicionális kalkulusban, ha a
formula akkor és csak akkor vezethető le a klasszikus propozicionális kalkulusban, ha a 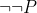 formula levezethető az intuicionista megfelelőjében. Sőt, negációval kezdődő formulákra:
formula levezethető az intuicionista megfelelőjében. Sőt, negációval kezdődő formulákra: 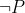 akkor és csak akkor vezethető le a klasszikus propozicionális logikában, ha az levezethető az intuicionista propozicionális logikában [10]. A predikátumkalkulus esetére egy ennél bonyolultabb – a „negatív fordítás” fogalmát használó – tétel adható, amelyet egymástól függetlenül Gödel és Gentzen bizonyított be [13].
akkor és csak akkor vezethető le a klasszikus propozicionális logikában, ha az levezethető az intuicionista propozicionális logikában [10]. A predikátumkalkulus esetére egy ennél bonyolultabb – a „negatív fordítás” fogalmát használó – tétel adható, amelyet egymástól függetlenül Gödel és Gentzen bizonyított be [13].
Heyting – Kroneckerrel ellentétben – a természetes számoknak sem tulajdonított semmiféle transzcendentális, gondolkodástól független létezést. Szerinte minden matematikai objektum – még ha talán független is az egyedi gondolati tevékenységtől – lényegét tekintve az emberi gondolkodás által meghatározott. Azonban Brouwer és Heyting filozófiai nézeteinek elfogadása nem szükséges az intuicionista matematikához, Dummett például egy wittgensteiniánus jelentéselméletre támaszkodva, nyelvfilozófiai alapokon érvelt a konstruktív logikai konstansok kizárólagos elfogadása mellett [4].
Brouwer (és tanítványa Heyting) matematikája még tartalmazott absztrakt fogalmakat, például: halmazokat és kiválasztási sorozatokat. Több matematikus kritizálta az absztrakt fogalmak használatát a matematikában, például: Kronecker, Skolem és Goodstein [12]. Ezen matematikusok egy nagyon korlátozott konstruktív matematika bevezetését javasolták, amelyben csak szigorúan véges matematikai objektumok használata van megengedve (mint amilyen egy természetes szám) és ezeken az objektumokon csak konkrét (effektív) kombinatorikus műveleteket szabad értelmezni (mint amilyet például egy szorzótábla definiál). Természetesen, a finitizmus teljesen konstruktív, és így része az intuicionista matematikának. A finitista matematika feltűnik David Hilbert (1862–1943) német matematikus programjában is. Hilbert kifejtette, hogy a matematikai axiómarendszerek konzisztenciáját véges (finit) – a végtelenség matematikai fogalmától mentes – eszközökkel kell bizonyítani, és ezáltal kell a matematikát véglegesen biztos alapokra helyezni. Kurt Gödel (1906–1978) osztrák logikus nemteljességi tételeit [11] általában úgy interpretálják, mint amelyek metamatematikai bizonyítását adják annak, hogy Hilbert bizonyításelméleti programja megvalósíthatatlan [10]. A finitizmusnak egy még radikálisabb változata is ismert, az ún. ultrafinitizmus. Például, Borel úgy gondolta, hogy egy nagyon nagy véges objektum (pl.: szám) legalább olyan problematikus mint egy végtelen. Direkt módon megfogalmazott olyan kérdéseket, hogy például a 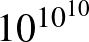 ténylegesen egy véges számnak tekinthető-e. A XX. század második felében történtek kísérletek az „alkalmas” vagy „kezelhető” (feasible) számok fogalmának megalkotására.
ténylegesen egy véges számnak tekinthető-e. A XX. század második felében történtek kísérletek az „alkalmas” vagy „kezelhető” (feasible) számok fogalmának megalkotására.
A konstruktív rekurzív matematika főleg Andrej Andrejevics Markov (1903–1979) nevéhez fűződik, és az algoritmusok vagy rekurzív függvények elméletén nyugszik. Primitív rekurzív függvényeket először Gödel használt nemteljességi tételeinek bizonyításához (1931). Alonzo Church (1903–1995) dolgozta ki (teljesen más alapokon) a 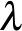 -kalkulust (1932), amely elmélet csak
-kalkulust (1932), amely elmélet csak 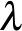 -absztrakciót használ és benne minden rekurzív függvény
-absztrakciót használ és benne minden rekurzív függvény 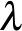 -definiálható [12]. Tőle függetlenül 1937-ben Alan Mathison Turing (1912–1954) bevezette az absztrakt matematikai gépek egy osztályát: a Turing-gépeket. A Turing-gépekkel kiszámítható függvények osztálya megegyezik a Church-féle
-definiálható [12]. Tőle függetlenül 1937-ben Alan Mathison Turing (1912–1954) bevezette az absztrakt matematikai gépek egy osztályát: a Turing-gépeket. A Turing-gépekkel kiszámítható függvények osztálya megegyezik a Church-féle 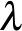 -kalkulussal kiszámítható függvények osztályával. Church tézise, amely azonosítja a „hatékonyan kiszámíthatóság” és a „rekurzívan kiszámíthatóság” fogalmát Church–Turing-tézis néven vált ismerté. Ezt a tézist Markov népszerűsítette és fektette le konstruktív matematikája alapjait: (1) a matematika objektumai különböző ábécék fölötti szavak; (2) realizálható absztrakció megengedett a matematikában, de nem megengedhetőek az aktuális végtelent használó absztrakciók. Markov a normál algoritmusok elméletén keresztül formalizálta matematikáját. Elmélete tekinthető úgy, mint egy rekurzív matematika intuicionista logikai alapokon. Bizonyos értelemben azonban Markov szigorúbb mint az intuicionisták, ugyanis csak olyan kiválasztási sorozatokat enged meg, amelyek egy véges algoritmus (például egy Turing-gép) által előre meghatározottak [13]. Markov más tekintetben azonban engedékenyebb az intuicionistáknál, amire példaként a Markov-elvet (Markov's principle) hozhatjuk. Az elv egyszerűen azt mondja ki, hogy ha lehetetlen, hogy egy bizonyos Turing-gép örökké fut, akkor létezik egy olyan algoritmus, amely a kimenetet előállítja és fel kell tennünk, hogy a gép egyszer megáll (terminál). Bináris sorozatokra ezt az elvet például úgy mondhatjuk ki, hogy ha egy sorozatra ellentmondás, hogy minden tagja egyenlő 0-val, akkor létezik egy olyan tagja a sorozatnak amely egyenlő 1-gyel. Az intuicionisták ezt az elvet (mivel a kizárt harmadik elvének átfogalmazása), mint intuitívan nem tisztát, elutasították [12].
-kalkulussal kiszámítható függvények osztályával. Church tézise, amely azonosítja a „hatékonyan kiszámíthatóság” és a „rekurzívan kiszámíthatóság” fogalmát Church–Turing-tézis néven vált ismerté. Ezt a tézist Markov népszerűsítette és fektette le konstruktív matematikája alapjait: (1) a matematika objektumai különböző ábécék fölötti szavak; (2) realizálható absztrakció megengedett a matematikában, de nem megengedhetőek az aktuális végtelent használó absztrakciók. Markov a normál algoritmusok elméletén keresztül formalizálta matematikáját. Elmélete tekinthető úgy, mint egy rekurzív matematika intuicionista logikai alapokon. Bizonyos értelemben azonban Markov szigorúbb mint az intuicionisták, ugyanis csak olyan kiválasztási sorozatokat enged meg, amelyek egy véges algoritmus (például egy Turing-gép) által előre meghatározottak [13]. Markov más tekintetben azonban engedékenyebb az intuicionistáknál, amire példaként a Markov-elvet (Markov's principle) hozhatjuk. Az elv egyszerűen azt mondja ki, hogy ha lehetetlen, hogy egy bizonyos Turing-gép örökké fut, akkor létezik egy olyan algoritmus, amely a kimenetet előállítja és fel kell tennünk, hogy a gép egyszer megáll (terminál). Bináris sorozatokra ezt az elvet például úgy mondhatjuk ki, hogy ha egy sorozatra ellentmondás, hogy minden tagja egyenlő 0-val, akkor létezik egy olyan tagja a sorozatnak amely egyenlő 1-gyel. Az intuicionisták ezt az elvet (mivel a kizárt harmadik elvének átfogalmazása), mint intuitívan nem tisztát, elutasították [12].
Sokan vélték úgy, hogy a kizárt harmadik elvének elutasítása rendkívül korlátozottá teszi az intuicionista matematikát, például Hilbert a „Grundlagen der Mathematik” (1928) című művében így írt: „a kizárt harmadik elvének kihagyása a matematikából ugyanolyan, mintha például a csillagászokat megfosztanánk a teleszkóptól vagy a boxolókat attól, hogy az öklüket használják”. Ezen nézetek radikálisan megváltoztak, miután Erret Bishop (1928–1983) publikálta „A konstruktív analízis megalapozása” (1967) című könyvét [1], amelyben a modern analízis nagy részét intuicionista alapokon újra felépítette. Olyan absztrakt tételek konstruktivista változatát találjuk könyvében, mint amilyen a Stone–Weierstrass-tétel, Hahn–Banach-tétel, Hilbert-térbeli önadjungált operátorok spektráltétele, az absztrakt integrálok Lebesgue-féle konvergenciatétele és olyan fogalmak intuicionista megfelelőit adta meg, mint a Haar-mérték és a Fourier-transzformáció [12]. Bishop elméletének egyik alapgondolata, hogy minden matematikának numerikus jelentéssel kell rendelkeznie. Ezen nézete közelebb áll Kronecker „aritmetizálási” programjához, mint Brouwer és Heyting megközelítéséhez, amelyben a természetes számok is csak az emberi elme termékei.
Bruce Pourciau álláspontja szerint [8] egy kuhni értelemben vett tudományos forradalom [7] elméletileg lehetséges a matematikában. Azonban eddig még nem tudunk róla, hogy a matematikában valaha lezajlott volna olyasfajta tudományos forradalom, amely után az új paradigmában a régi paradigma állításai inkoherensnek, nem megfelelően alátámasztottnak vagy egyszerűen hamisnak bizonyultak. Pourciau véleménye szerint azonban az intuicionizmus egy ilyen paradigmaváltás lehetőségét hordozta magában, de – főképp történeti okokból (például Brouwer extravagáns nézetei miatt) – elbukott.
Pourciau egy másik cikkében [9] – amit egy színdarab formájában írt meg – azon az állásponton van, hogy ha néhány nagyon egyszerű (szinte önevidensnek látszó) alapelvet elfogadunk a tudományos vizsgálatok alapelveiként, akkor ezekből már következik az intuicionizmus. Ezen elvek a következők:
(1) Ismernünk kell egy állítás jelentését, mielőtt azt vizsgálnánk, hogy igaz-e.
(2) Ne építsünk teljesen megalapozatlan feltevésekre.
(3) Az egyszerűtől haladjuk a kevésbé egyszerű felé.
A matematika elsődlegességét a logikával szemben (Brouwer szellemében) például (1) és (2) támasztja alá: mivel a logika az állítások jelentésétől függetlenül vizsgálja igazságértéküket, ez ellentmond (1)-nek, a kétértékűség kritika nélkül való elfogadása pedig (2)-nek – állítja Pourciau [9]. A természetes számok halmazelméleti felépítése ellen a (3) feltétel alapján lehet érvelni, mivel a természetes számok fogalma sokkal világosabb, mint mondjuk a Zermelo–Fraenkel-féle axiómarendszer. Pourciau álláspontja szerint (1)–(3) elfogadásával nem egyeztethető össze a klasszikus matematika, azonban az intuicionista már igen.
Tehát a matematika antirealista megközelítései – például az intuicionizmus, illetve a konstruktivizmus – szerint nem léteznek elmefüggetlen matematikai igazságok. Az első matematikusok, akik kritizálták a realista megközelítést Kronecker, Baire, Borel, Lebesgue, Lusin és Poincaré voltak. Brouwer fogalmazta meg elsőként az intuicionizus programját, műveiben erős Kant és Schopenhauer filozófiájának hatása. Brouwer több ellenpéldán keresztül megpróbálta megcáfolni a kizárt harmadik elvét. Tanítványának, Heytingnek a munkássága nyomán nyilvánvalóvá vált, hogy az intuicionizmus precíz formába önthető és formális-axiomatikus elméletté tehető. Az intuicionista logikára hatékony konstruktív matematika építhető, amelyre egy példa Bishopnak a konstruktív analízist megalapozó munkája. Dummett nyelvfilozófiai alapokon érvelt az intuicionista logika elfogadása mellett, míg Pourciau tudománymetodikai alapokon védte az intuicionzimust, ami szerinte egy elbukott matematikai (kuhni értelemben vett) tudományos forradalom.
Az intuicionizmus filozófiai alátámasztásával kapcsolatban több ellenvetés megfogalmazható. Például, Edmund Husserl (1858–1938) kritikája a logika pszichológiai megalapozására vonatkozóan [6] – noha jóval Brouwer munkái előtt született – értelmezhető az intuicionizmus kritikájaként is. Egy másik példa lehetne Gödel, aki maga is érvelt [7] a formalizmus és az intuicionizmus ellen, és azon a véleményen volt, hogy: „az emberi elme számára […] egyetlen tartható álláspont van csak: a platonizmus”. Azonban, az intuicionista, illetve a konstruktivista (antirealista) álláspontok tagadhatatlan erénye, hogy rávilágítanak a klasszikus (realista) matematikafelfogás gyenge pontjaira és technikailag is elfogadható alternatívát kínálnak.
Irodalomjegyzék
[1] Bishop, E. (1967): Foundations of Constructive Analysis. McGraw-Hill, New York.
[2] Dummett, Michael (1977): Elements of Intuitionism. Clarendon Press, Oxford.
[3] Dummett, Michael (1982): Realism. Synthese Vol. 55, 55–112.
[4] Dummett, Michael (1973): The Philosophical Basis of Intuitionistic Logic. In: Truth and Other Enigmas, Duckworth (1978) 215–247.
[5] Gödel, Kurt (1951): Néhány tétel a matematika megalapozásáról és ezek következményei (Gibbs Lecture) In: Csaba Ferenc (szerk.): A matematika filozófiája a 21. század küszöbén. Osiris Kiadó, Budapest, 2003, 61–89.
[6] Husserl, E. (1900): Logische Untersuchungen, Erster Teil: Prolegomena zur reinen Logik (English trans. by J. N. Findlay, English title: Logical Investigations, London: Routledge, 1900/01; 1913).
[7] Kuhn, Thomas (1962): A tudományos forradalmak szerkezete. Osiris Kiadó, Budapest, 2000.
[8] Pourciau, Bruce (2000): Intuitionism as a (Failed) Kuhnian Revolution in Mathematics. Studies in History and Philosophy of Science, Vol. 31, No. 2, 297–329, Elsevier Science.
[9] Pourciau, Bruce (1999): The Education of a Pure Mathematician. The American Mathematical Monthly, Oct. 1999, Vol. 106, No. 8, 720–732.
[10] Ruzsa Imre; Máté András (1997): Bevezetés a modern logikába. Osiris Kiadó, Budapest.
[11] Smullyan, Raymond (1992): Gödel nemteljességi tételei. Typotex Kiadó, Budapest, 1999.
[12] Troelstra, Anne Sjerp; Van Dalen, Dirk (1988): Constructivism in Mathematics. Vol. 1, North-Holland, Amsterdam.
[13] Zalta, Edward N. (editor): The Stanford Encyclopedia of Philosophy (2019): Intuitionism in the Philosophy of Mathematics, https://plato.stanford.edu/entries/intuitionism/.
SZTAKI, ELTE Matematikai Intézet
Lábjegyzet
- 1 Logikai konstansok például a logikai összekötőjelek (
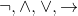 ) és a kvantorok:
) és a kvantorok: 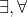 .
.









