A hétköznapi életben két dolgot sokszor hasonlónak nevezünk, ha valamilyen (az aktuális feladathoz jól passzoló) mérőszám szerint kicsi az eltérésük. Vagy ha úgy tetszik: valamilyen alkalmas távolságfogalom szerint a távolságuk kicsi. Nézzünk egy egyszerű példát: tömegközlekedéssel akarunk eljutni a moziba, és azt látjuk, hogy a buszmegálló 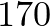 méterre van a mozitól, a villamosmegálló pedig
méterre van a mozitól, a villamosmegálló pedig 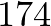 méterre. Ilyenkor azt mondhatjuk, hogy a feladat szempontjából a két megálló hasonló, hiszen az általuk meghatározott két útvonal eltérése kicsi. Két útvonal eltérésén itt most a
méterre. Ilyenkor azt mondhatjuk, hogy a feladat szempontjából a két megálló hasonló, hiszen az általuk meghatározott két útvonal eltérése kicsi. Két útvonal eltérésén itt most a 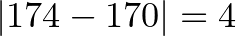 mérőszámot értjük, ami ha gyaloglásról van szó, méterben számolva valóban elenyésző.
mérőszámot értjük, ami ha gyaloglásról van szó, méterben számolva valóban elenyésző.
Ebben a rövid írásban két távolságfogalomról lesz szó, a Hausdorff-távolságról, és a Gromov–Hausdorff-távolságról. Annak idején mindkettőt tisztán elméleti okokból definiálták, manapság azonban (a továbbfejlesztett verzióikkal együtt) az alkalmazott tudományokban is komoly szerepet játszanak.
1. Halmazok Hausdorff-távolsága
Két lépésben fogunk eljutni a Gromov–Hausdorff-távolsághoz. Elsőként a Hausdorff-távolságról lesz szó, ami azt méri, hogy egy adott tér részhalmazai milyen távol vannak egymástól. Pongyolán szólva, két halmaz,  és
és 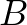 akkor van egymáshoz közel, ha
akkor van egymáshoz közel, ha 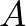 minden eleméhez van olyan eleme
minden eleméhez van olyan eleme 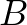 -nek, ami hozzá közel van, és megfordítva,
-nek, ami hozzá közel van, és megfordítva, 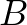 minden eleméhez található olyan elem
minden eleméhez található olyan elem 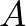 -ban, ami hozzá közel van. Nézzünk egy nagyon egyszerű példát: vegyük a piros pontokból álló
-ban, ami hozzá közel van. Nézzünk egy nagyon egyszerű példát: vegyük a piros pontokból álló 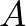 halmazt és a kék pontokból álló
halmazt és a kék pontokból álló 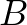 halmazt.
halmazt.

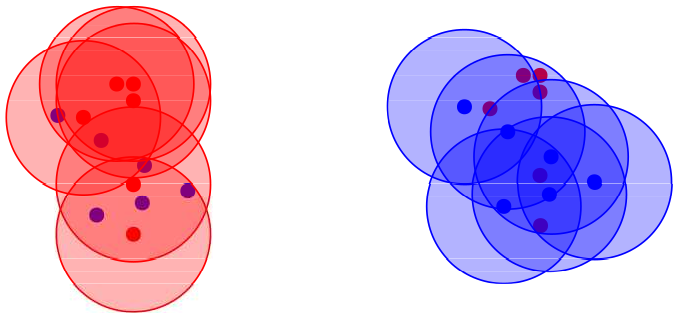
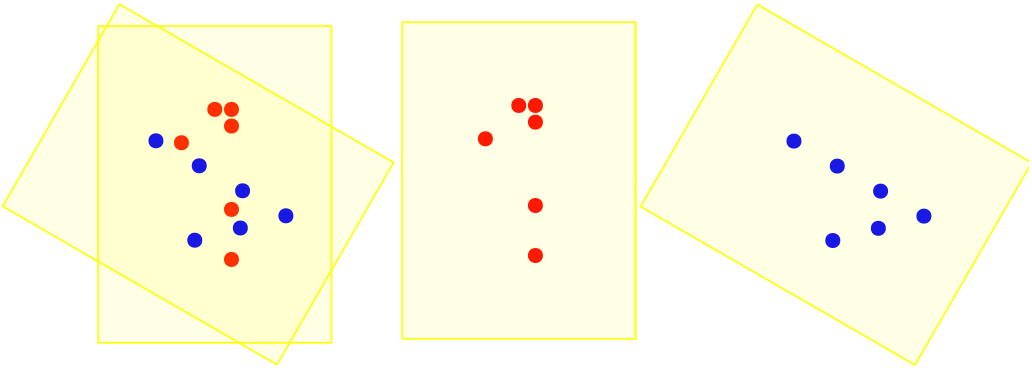
1. ábra. ![]() halmaz: piros pontok,
halmaz: piros pontok, 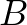 halmaz: kék pontok.
halmaz: kék pontok.
Az 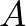 halmazt befedhetjük
halmazt befedhetjük  sugarú gömbökkel úgy, hogy minden egyes pontjára ráteszünk egyet-egyet, jelöljük az így kapott halmazt
sugarú gömbökkel úgy, hogy minden egyes pontjára ráteszünk egyet-egyet, jelöljük az így kapott halmazt 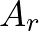 -rel:
-rel:

2. ábra. 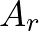 : az
: az 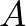 halmaz befedése
halmaz befedése  sugarú gömbökkel.
sugarú gömbökkel.
Olyan  számot keresünk, amelyre az
számot keresünk, amelyre az 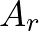 halmaz lefedi
halmaz lefedi 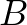 -t is, és a hasonlóképp elkészített
-t is, és a hasonlóképp elkészített 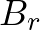 halmaz is lefedi
halmaz is lefedi 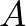 -t.
-t.
3.ábra. 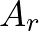 lefedi
lefedi 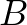 -t, és
-t, és  is lefedi
is lefedi 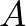 -t.
-t.
A legkisebb ilyen  számot nevezzük
számot nevezzük 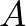 és
és 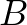 Hausdorff-távolságának. Ezt a távolságot Felix Hausdorff vezette be az 1914-ben megjelent, A halmazelmélet alapjai című könyvében. Manapság rengeteget használják többek közt a számítógépes látásban: tipikus feladat, hogy egy képen be kell azonosítani egy objektumot (lásd például [5] 858. oldal, vagy [6]). Az alábbi ábrán a bal oldali kis repülőt kell megtalálni a középső képen. A jobb oldali képen láthatjuk, hogy a kép mely részén lép fel az alakzatok közti legkisebb Hausdorff-távolság.
Hausdorff-távolságának. Ezt a távolságot Felix Hausdorff vezette be az 1914-ben megjelent, A halmazelmélet alapjai című könyvében. Manapság rengeteget használják többek közt a számítógépes látásban: tipikus feladat, hogy egy képen be kell azonosítani egy objektumot (lásd például [5] 858. oldal, vagy [6]). Az alábbi ábrán a bal oldali kis repülőt kell megtalálni a középső képen. A jobb oldali képen láthatjuk, hogy a kép mely részén lép fel az alakzatok közti legkisebb Hausdorff-távolság.

4. ábra. A képek Grégoire-tól és Bouillot-tól származnak [6]

Felix Hausdorff a XX. századi matematika egyik legnagyobb hatású alakja. A topológia, a halmazelmélet, a mértékelmélet és a funkcionálanalízis területén is maradandót alkotott, de nevezhetnénk akár ezen tudományterületek egyik megalapozójának is. Egyebek mellett ő vezette be a fraktálok elméletében oly fontos mérték és dimenzió fogalmakat, amelyeket ma már Hausdorff-mértéknek és Hausdorff-dimenziónak neveznek. Paul Mongré néven irodalmi munkákat is publikált [9]. 1900-ban kiadott egy verseskötetet Ekstasen címmel, a Den Ungeflügelten című verse németül és angolul elolvasható a [3] cikkben
A Hausdorff-távolság fenti bevezetésénél több ponton is pongyolák voltunk. Jöjjön most a pontos definíció. Egy 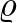 függvénnyel ellátott
függvénnyel ellátott 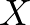 halmazt – röviden: az
halmazt – röviden: az 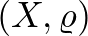 párt – metrikus térnek nevezünk, ha
párt – metrikus térnek nevezünk, ha 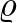 teljesít három nagyon természetes tulajdonságot (az ilyen függvényeket metrikának nevezzük):
teljesít három nagyon természetes tulajdonságot (az ilyen függvényeket metrikának nevezzük):

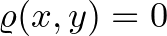 akkor és csak akkor, ha
akkor és csak akkor, ha 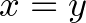 . Tehát két pont pontosan akkor van egymástól nulla
. Tehát két pont pontosan akkor van egymástól nulla  -távolságra, ha
-távolságra, ha 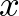 és
és  ugyanaz a pont.
ugyanaz a pont.

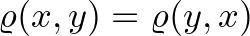 . Tehát az
. Tehát az 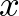 pont
pont 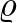 -távolsága
-távolsága  -tól ugyanannyi, mint az
-tól ugyanannyi, mint az  pont
pont 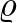 -távolsága
-távolsága 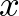 -től.
-től.

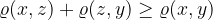 . Tehát egy harmadik
. Tehát egy harmadik 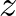 pontot beiktatva, az
pontot beiktatva, az 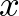 és
és 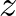 , valamint
, valamint 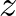 és
és 
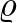 -távolságát megmérve és összeadva legalább akkora értéket kell kapnunk, mintha közvetlenül az
-távolságát megmérve és összeadva legalább akkora értéket kell kapnunk, mintha közvetlenül az 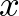 és
és 
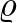 -távolságát mértük volna meg. (Ez az úgynevezett háromszög-egyenlőtlenség.)
-távolságát mértük volna meg. (Ez az úgynevezett háromszög-egyenlőtlenség.)
Egy metrikus térben ugyanúgy vezetjük be az 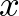 középpontú
középpontú  sugarú gömb fogalmát, mint a síkon: azon
sugarú gömb fogalmát, mint a síkon: azon  pontok halmaza, amelyekre
pontok halmaza, amelyekre 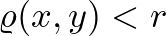 teljesül. Hasonlóan a fentiekhez,
teljesül. Hasonlóan a fentiekhez, 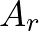 -rel és
-rel és 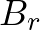 -rel fogjuk jelölni azokat a halmazokat, amelyeket úgy kapunk, hogy
-rel fogjuk jelölni azokat a halmazokat, amelyeket úgy kapunk, hogy 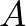 illetve
illetve 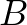 minden pontjára ráteszünk egy-egy
minden pontjára ráteszünk egy-egy  sugarú gömböt. Olyan
sugarú gömböt. Olyan  -eket keresünk, amelyekre
-eket keresünk, amelyekre 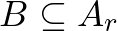 és
és 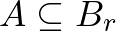 egyszerre teljesül. Lehet, hogy nincs legkisebb ilyen
egyszerre teljesül. Lehet, hogy nincs legkisebb ilyen  , de a
, de a 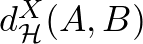 -vel jelölt Hausdorff-távolság alábbi definíciója értelmes:
-vel jelölt Hausdorff-távolság alábbi definíciója értelmes:
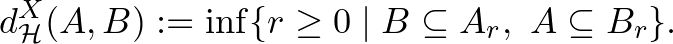
A jelölésben feltüntettük, hogy 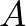 és
és 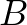 az
az 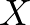 térnek a részhalmazai, később ez fontos lesz.
térnek a részhalmazai, később ez fontos lesz.
Az alakfelismerés szempontjából a Hausdorff-távolságnak van egy gyenge pontja. Gondoljunk arra, hogy mi történne, ha a 4. ábrán látható kis repülőt (amit a középső képen fel kell ismerni) 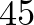 fokkal elforgatnánk a pilótafülke körül. Az így kapott képnek és a középső képen látható másának Hausdorff-távolsága már nagy lenne, így az az eljárás, ami a kicsi Hausdorff-távolságot keresi, már nem találná őket hasonlónak. Térjünk vissza az 1. ábrán látható ponthalmazokhoz. Láttuk, hogy elég nagy
fokkal elforgatnánk a pilótafülke körül. Az így kapott képnek és a középső képen látható másának Hausdorff-távolsága már nagy lenne, így az az eljárás, ami a kicsi Hausdorff-távolságot keresi, már nem találná őket hasonlónak. Térjünk vissza az 1. ábrán látható ponthalmazokhoz. Láttuk, hogy elég nagy  -re van szükségünk, hogy
-re van szükségünk, hogy 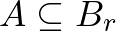 és
és 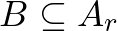 is fennálljon. Hogy milyen értelemben nagy ez az
is fennálljon. Hogy milyen értelemben nagy ez az  , az rögtön kiderül. Képzeljük úgy, hogy a kék és piros ponthalmaz egy-egy üveglapra van felfestve.
, az rögtön kiderül. Képzeljük úgy, hogy a kék és piros ponthalmaz egy-egy üveglapra van felfestve.
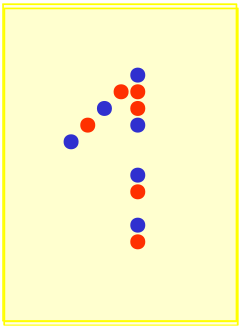
6.ábra.  és
és  egy-egy üveglapra felfestve, egymásra helyezve és külön-kölön.
egy-egy üveglapra felfestve, egymásra helyezve és külön-kölön.
Ha jogunkban áll ezt a két üveglapot mozgatni, sőt akár meg is lehet őket fordítani, akkor könnyen észrevehetjük, hogy a két alakzat nagyon hasonló.
7. ábra. 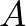 és
és 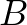 egymáshoz igazítva.
egymáshoz igazítva.
Látható, hogy a korábbinál sokkal kisebb  is elegendő, hogy
is elegendő, hogy 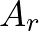 lefedje
lefedje 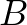 -t, és
-t, és 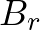 is lefedje
is lefedje 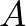 -t.
-t.
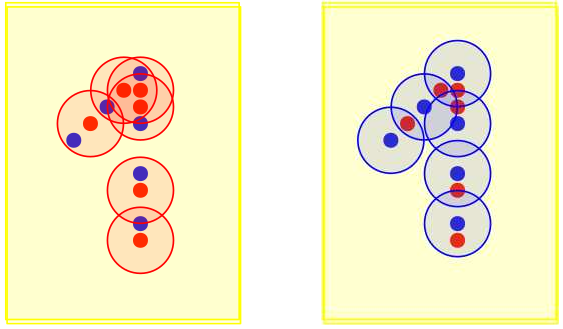
8.ábra. A korábbinál sokkal kisebb  is elegendő.
is elegendő.
2. Metrikus terek Gromov–Hausdorff-távolsága
Azt láttuk, hogy ugyanazoknak a halmazoknak különböző realizációihoz más Hausdorff-távolság tartozik. A fenti eljárással akár két különböző térben lévő halmaz Hausdorff-távolságát is megmérhetjük. Legyen 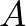 az
az 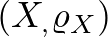 ,
, 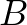 pedig az
pedig az 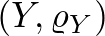 metrikus tér egy-egy részhalmaza. Legyen továbbá
metrikus tér egy-egy részhalmaza. Legyen továbbá 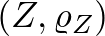 egy harmadik metrikus tér, amelybe
egy harmadik metrikus tér, amelybe 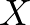 és
és 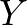 is izometrikusan beágyazható, azaz léteznek olyan
is izometrikusan beágyazható, azaz léteznek olyan 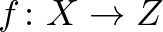 és
és  függvények, amelyekre
függvények, amelyekre 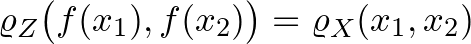 minden
minden 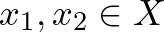 -re és
-re és 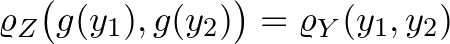 minden
minden  -ra. Ekkor megadhatjuk
-ra. Ekkor megadhatjuk 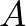 és
és 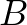 Hausdorff-távolságát a
Hausdorff-távolságát a 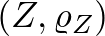 metrikus térben az
metrikus térben az 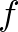 és
és 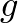 realizációk mentén:
realizációk mentén:
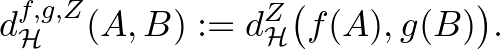 |
(1) |
A Gromov által felfedezett távolság célja, hogy különböző metrikus terek hasonlóságát mérje: két metrikus tér 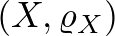 és
és 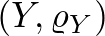 Gromov–Hausdorff-távolsága azt mondja meg, hogy a két tér milyen távol van attól, hogy egymással izomorf legyen. (Két metrikus tér izomorf, ha van köztük olyan kölcsönösen egyértelmű megfeleltetés, amely megőrzi a távolságot.)
Gromov–Hausdorff-távolsága azt mondja meg, hogy a két tér milyen távol van attól, hogy egymással izomorf legyen. (Két metrikus tér izomorf, ha van köztük olyan kölcsönösen egyértelmű megfeleltetés, amely megőrzi a távolságot.)
Ha a fenti (1) formulába 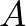 helyére magát
helyére magát  -et,
-et, 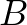 helyére pedig
helyére pedig 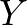 -t helyettesítjük, akkor azt kapjuk, hogy
-t helyettesítjük, akkor azt kapjuk, hogy 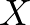 és
és 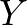 realizációi az
realizációi az 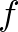 és
és 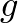 függvények mentén mennyire térnek el egymástól a
függvények mentén mennyire térnek el egymástól a 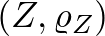 térben. Két tér
térben. Két tér 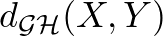 -nal jelölt Gromov–Haudorff-távolságát úgy kapjuk meg, hogy vesszük
-nal jelölt Gromov–Haudorff-távolságát úgy kapjuk meg, hogy vesszük 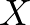 és
és 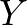 összes lehetséges
összes lehetséges 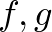 realizációját az összes lehetséges
realizációját az összes lehetséges 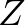 térben, kiszámítjuk a
térben, kiszámítjuk a  értékeket, és vesszük ezeknek a legnagyobb alsó korlátját:
értékeket, és vesszük ezeknek a legnagyobb alsó korlátját:

A Gromov–Hausdorff-távolságnak (és a bizonyos értelemben vett továbbfejlesztésének, így például a Gromov–Wasserstein-távolságnak) is vannak modern alkalmazásai például az alakfelismerésben és a gépi tanulásban, lásd például [1], [4], [7], [2]. Itt most ezekre nem térünk ki. A cikket a Gromov–Hausdorff-tér és a Gromov–Hausdorff-konvergencia vázlatos bemutatásával zárjuk. Ezek a fogalmak fontos szerepet játszottak a híres Milnor-Wolf sejtés igazolásánál (lásd a Gromovról szóló színes írást a cikk végén).
Be lehet bizonyítani, hogy a fent bevezetett 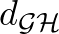 távolsággal a kompakt metrikus terek izometriaosztályai maguk is egy kompakt metrikus teret alkotnak, ezt nevezik a Gromov–Hausdorff-térnek. Mint minden metrikus térben, itt is bevezethető a konvergencia fogalma: az
távolsággal a kompakt metrikus terek izometriaosztályai maguk is egy kompakt metrikus teret alkotnak, ezt nevezik a Gromov–Hausdorff-térnek. Mint minden metrikus térben, itt is bevezethető a konvergencia fogalma: az 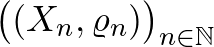 térsorozat konvergál az
térsorozat konvergál az 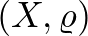 metrikus térhez, ha a
metrikus térhez, ha a 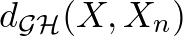 számsorozat 0-hoz tart.
számsorozat 0-hoz tart.
Nézzünk egy egyszerű példát: tegyük fel, hogy egy négyzetlapra illesztett négyzetrácson élünk. (Legyen a rács az 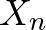 , két pont
, két pont 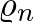 távolsága pedig legyen az őket összekötő legrövidebb út hossza.) Mondhatjuk, hogy ez a négyzetlapnak egy leegyszerűsített változata. Az egyszerűsítés ára, hogy a kék
távolsága pedig legyen az őket összekötő legrövidebb út hossza.) Mondhatjuk, hogy ez a négyzetlapnak egy leegyszerűsített változata. Az egyszerűsítés ára, hogy a kék  pontból a piros
pontból a piros 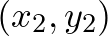 pontba csak meglehetősen szögletes utak mentén tudunk eljutni.
pontba csak meglehetősen szögletes utak mentén tudunk eljutni.
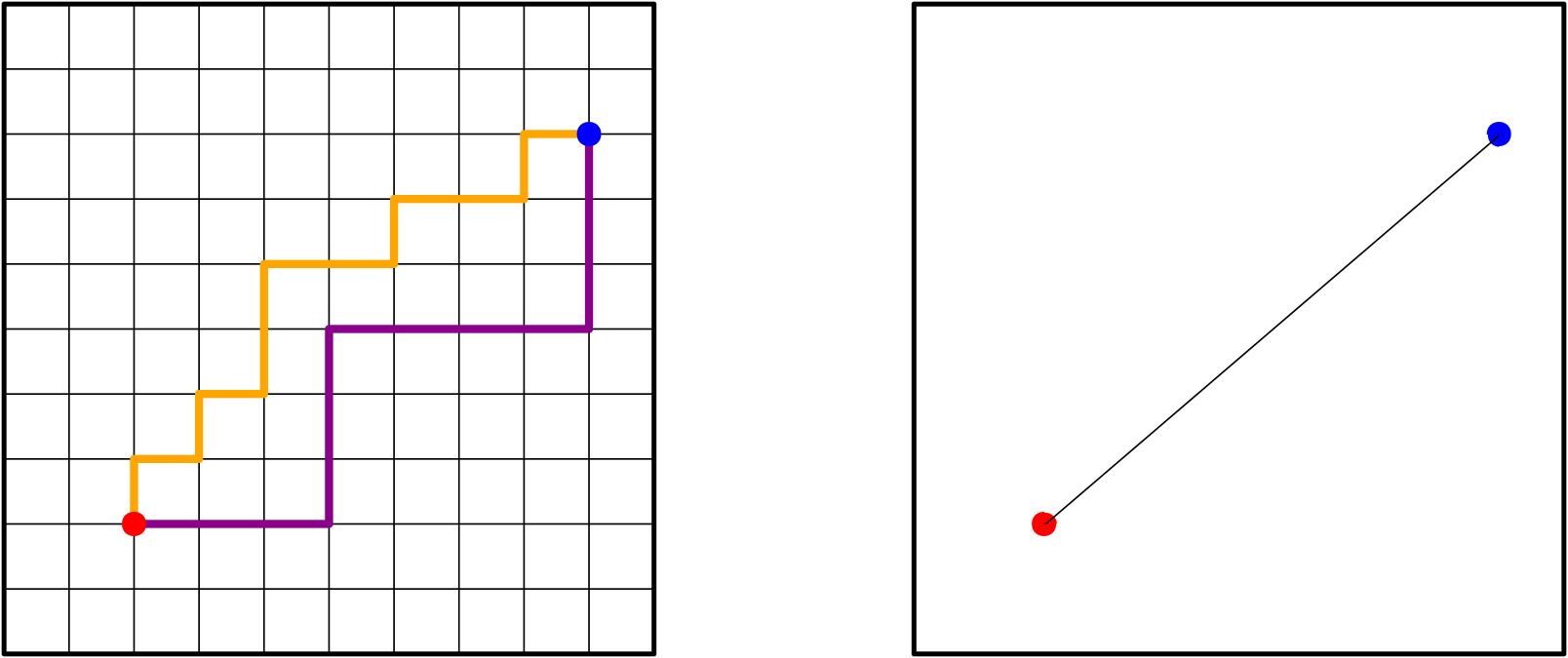
9. ábra. Legrövidebb út a rácson és a hagyományos négyzetlapon.
Persze gondolhatjuk, hogy minél finomabb rácsot veszünk, annál jobban fog hasonlítani az utunk a megszokotthoz, azaz ahhoz, amikor a négyzetlap két pontját egyenes vonallal kötjük össze.
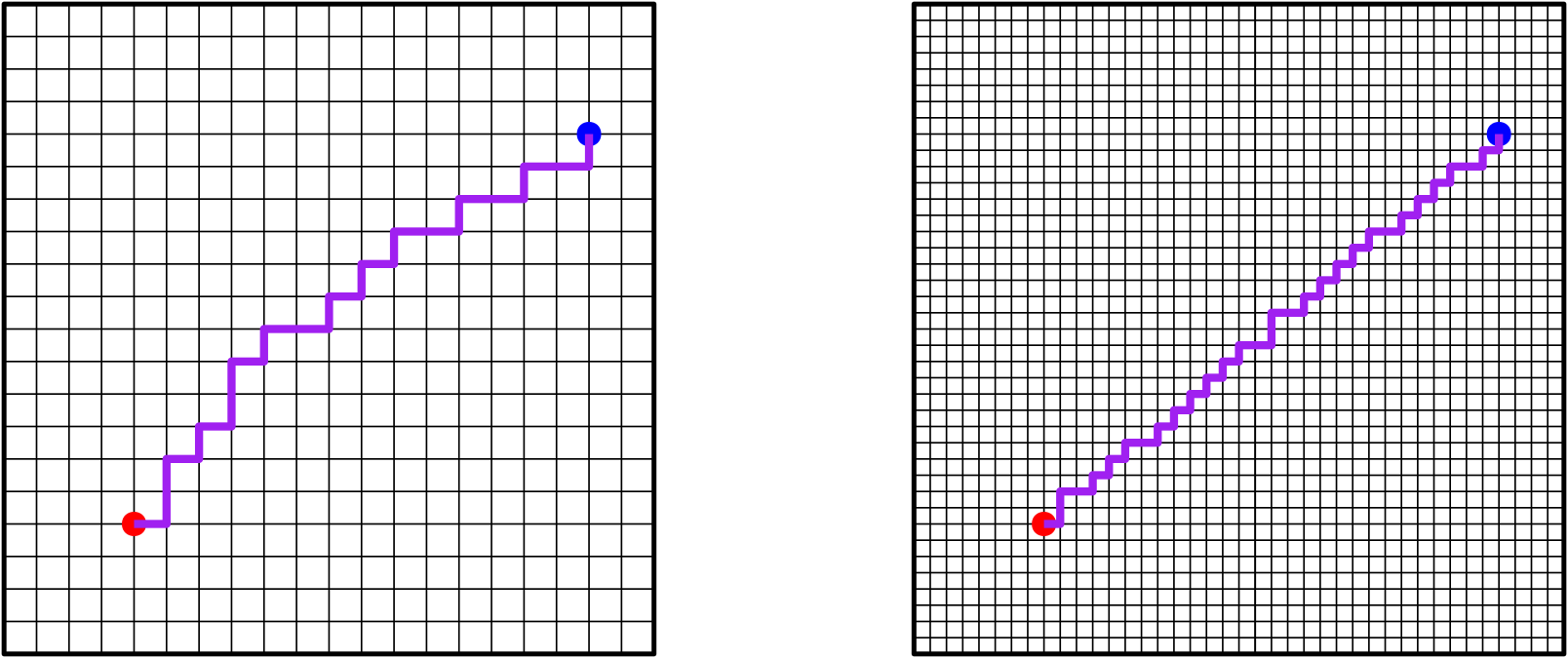
10. ábra. Út az egyre finomodó rácsokon.
A kérdés, hogy valóban a szokásos négyzetlapot kapjuk-e meg határértékben. Azt kell észrevenni, hogy bármilyen finom négyzetrácsot is választunk, és bármennyire is hasonlít a töröttvonalunk az egyenes vonalhoz, a töröttvonal hossza mindig  . Tehát az
. Tehát az  térsorozat Gromov–Hausdorff limesze a négyzetlap, de nem a hagyományos euklidészi távolsággal:
térsorozat Gromov–Hausdorff limesze a négyzetlap, de nem a hagyományos euklidészi távolsággal:  , hanem a
, hanem a 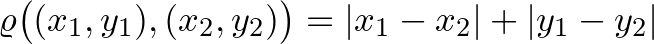 távolsággal.
távolsággal.

Mihail Gromov orosz–francia matematikus, a metrikus geometria, a szimplektikus geometria, és a geometriai csoportelmélet úttörője. Egyik leghíresebb eredménye a Milnor és Wolf nevéhez fűződő sejtés igazolása: egy végesen generált csoport pontosan akkor polinomiális növekedésű, ha van véges indexű nilpotens részcsoportja. Elnyerte többet közt az Élie Cartan-díjat, a Wolf-díjat, a Kiotó-díjat és az Abel-díjat. Mihail Gromov a 2005-ös Bolyai János nemzetközi matematikai díj kitüntetettje, 2010 óta a Magyar Tudományos Akadémia tiszteletbeli tagja.
Irodalomjegyzék
[1] Bronstein, A.M.; Bronstein, M.M.; Bruckstein, A.M.; Kimmel, R., Analysis of Two-Dimensional Non-Rigid Shapes, International Journal of Computer Vision, 78(1), 2007, 67–88.
[2] Chowdhury, S.; Miller, D.; Needham, T., Quantized Gromov–Wasserstein, ArXiv: 2104.02013.
[3] ELKINS, B., Felix Hausdorff’s Poem “Den Ungeflügelten”, Journal of Humanistic Mathematics, 11 (2), 2021, pages 405–408.
[4] Fehri, A.; Velasco-Forero, S.; Meyer, F., Characterizing Images by the Gromov-Hausdorff Distances Between Derived Hierarchies, 25th IEEE International Conference on Image Processing (ICIP), 2018, 1213–1217.
[5] Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J., Comparing images using the Hausdorff distance, IEEE Transactions on Pattern Analysis and Machine Intelligence, 15 (9), 1993, 850–863.
[6] Grégoire, N.; Bouillot, M., Hausdorff distance between convex polygons
[7] Mémoli, F., Gromov–Wasserstein Distances and the Metric Approach to Object Matching, Found Comput Math 11, 2011, 417–487.
[8] Mongré, P., Ekstasen, Verlag H. Seemann Nachf., Leipzig, 1900.
[9] Purkert, W, The double life of Felix Hausdorff/ Paul Mongré, The Mathematical Intelligencer, 30(4), 2008, 36–50.
Titkos Tamás
Rényi Alfréd Matematikai Kutatóintézet









