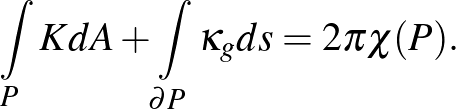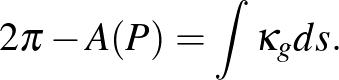Az akrobatika egyik népszerű ága, amikor akrobaták egy nagy fémkeret mozgását a testsúlyuk fémkereten belüli mozgatásával egyensúlyozva gurítják a fémkeretet a színpadon. Az egyik népszerű akrobatikus eszköz a német kerék. Két párhuzamos gyűrűből áll, amelyet fokok és fogantyúk kötnek össze (lásd 1. ábra), ezeket fogják az akrobaták.

1. ábra
Egy kevésbé ismert változata ezeknek az eszközöknek a cikk-cakk-gördülő, amely Toni Vighetto találmánya (lásd 2. ábra).

2. ábra
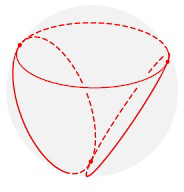
Mozgását a https://bit.ly/3wgmvEP oldal videója mutatja. Lényegében ugyanúgy mozog, mint a gömbicsavartkúp ([3]), amelyet a 3. ábrán látható módon konstruálunk két derékszögű egyenes kúpból.
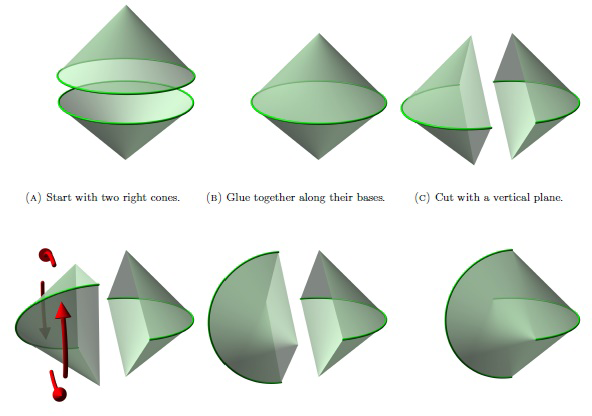
3. ábra
A 4. ábrán a gömbicsavartkúp mozgását látjuk a síkon.
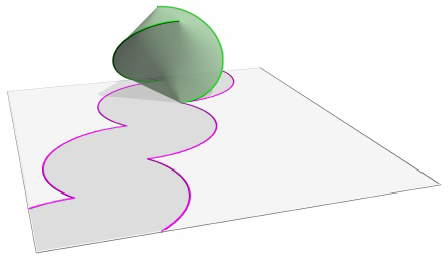
4. ábra
A cikk-cakk-gördülő eszköz esetében a gömbicsavartkúp félköríveit hurkok helyettesítik, amelyek szorosan közelítik a félköríveket. Az eszköznek azon részeit, amelyek kapcsolatba kerülnek a színpaddal, miközben az eszköz mozog, síneknek fogjuk nevezni. A maradék struktúra a síneket kapcsolja össze, és biztosítja a művésznek, hogy lépjen vagy megtartsa magát rajtuk.
Marco Paoletti, világhírű zsonglőr és cirkuszi artista a következő kérdést vetette fel a cikk-cakk-gördülő eszközzel kapcsolatban: jóllehet az eszköz cikk-cakk alakban mozog a színpadon, egy teljes fordulat után ugyanabba az irányba néz, mint a mozgás kezdetén. Nagy léptékben így egyenes vonalban mozog, akárcsak a német kerék. Ezért az akrobatának, hogy ki ne fusson a színpadról, meg kell állítania az eszközt és visszafelé haladnia vele, megtörve ezzel az előrehaladó mozgás lendületét. Marco azt kérdezte, lehetne-e konstruálni olyan eszközt, amelyik kiküszöböli ezt a problémát: például ha a cikk-cakk-gördülő két félköre különböző méretű lenne, akkor az eszköz kört írna le, miközben cikk-cakkban mozog? Henry Segerman a ([2]) cikkben ennek a kérdésnek a megválaszolásával foglalkozik, és javaslatot tesz néhány alternatív eszközre. A guruló eszközre a következő feltevést tesszük:
1. feltevés. Az eszköz tömegközéppontja nem változtatja a magasságát mozgás közben.
Ha ez a feltevés nem teljesül, akkor az eszköz mozgása során lesznek pillanatok, amikor a tömegközéppont magassága egy lokális minimumnál lesz. Egy ilyen pontból való elmozdulás munkát igényel az akrobata részéről. Ehhez elegendő súrlódás szükséges a keret és a színpad között a csúszás elkerülése érdekében. Az előadónak nem könnyű megtartania az eszközt egy bizonyos egyensúlyi pontnál, és nincs más választása, mint hagyja, hogy tovább guruljon. Mindezek korlátozzák, milyen módon használhatja az akrobata az eszközt. Ha az 1. feltevés teljesül, akkor az előadó minden konfigurációban kontrollálni tudja az eszköz mozgását. Elég, ha egy kicsit változtat a pozicióján, eltolva a keret és a saját közös tömegközéppontját, és így egyensúlyozza az eszközt.
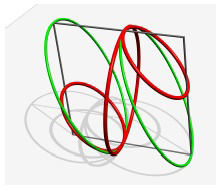
Marco kérdésére válaszolva megmutatjuk, hogy egy kevésbé szimmetrikus cikk-cakk-gördülő eszköz, amelynek két félköre különböző méretű, a 8. ábrán látható mozgást ír le a porondon, azaz három ciklus után visszatér az eredeti helyzetébe. Sajnos egy ilyen eszköz fizikai megvalósítása problémába ütközik, mivel ha állandó sűrűségű fémcsövekből készítjük el, akkor tömegközéppontja nem teljesíti az 1. feltevést. Ez a probléma elvileg kiküszöbölhető, ha a keretre bizonyos helyeken plusz súlyokat helyeznek el. Az 5. és a 6. tételek azt mutatják, hogy szükségszerűen nehéz olyan eszközt konstruálni, amely a színpadon marad, anélkül, hogy az akrobata megállítaná és visszafordítaná. Ha általánosítjuk a konstrukciónkat, és megengedünk többszörös hurkokat, akkor azonban lehetővé válik, hogy az 5. és a 6. tétel is teljesüljön. Két ilyen eszközt fogunk bemutatni. Az első (lásd 10/a. és 10/b. ábrák) az egyenes vonalú mozgáson kívül 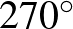 -os elfordulásra is képes (lásd 10/c. ábra). A második eszközzel (lásd 11/a. és 11/b. ábrák) a 11/c. ábrán látható köröket írhatjuk le a porondon.
-os elfordulásra is képes (lásd 10/c. ábra). A második eszközzel (lásd 11/a. és 11/b. ábrák) a 11/c. ábrán látható köröket írhatjuk le a porondon.
A gördülő eszköz konstrukciója, megvalósításának feltételei
Az 1. feltevéssel élve egy képzeletbeli gömböt rögzítünk a kerethez, amelynek sugara a tömegközéppont színpadtól mért távolsága. Ezt hívjuk gördülő gömbnek. Az eszköz mozgásának minden pillanatában a gördülő gömb egyetlen pontban érinti a színpadot. Ezeknek a pontoknak a nyomon követése két görbét állít elő:  -t a gördülő gömbön és
-t a gördülő gömbön és 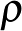 -t a színpad síkján. Az 5. ábra azt a példát mutatja, ahol
-t a színpad síkján. Az 5. ábra azt a példát mutatja, ahol  a teniszlabdagörbe, ami négy egybevágó félkörből áll.
a teniszlabdagörbe, ami négy egybevágó félkörből áll.
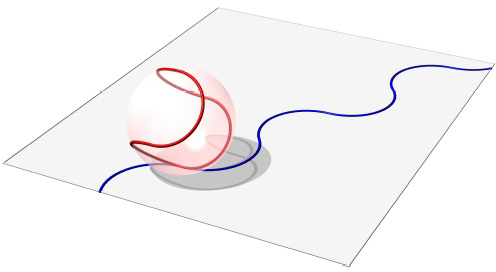
5. ábra
Általában, fel fogjuk tenni, hogy  egy szakaszonként sima egyszerű zárt görbe. Mostantól feltesszük, hogy a gördülő gömb sugara egységnyi. Legyen
egy szakaszonként sima egyszerű zárt görbe. Mostantól feltesszük, hogy a gördülő gömb sugara egységnyi. Legyen 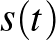 a
a  görbe természetes paraméterezése (egység sebességű paraméterezése). Legyen
görbe természetes paraméterezése (egység sebességű paraméterezése). Legyen 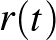 a megfelelő síkbeli
a megfelelő síkbeli 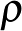 görbe természetes paraméterezése. Ha az eszközhöz rögzített vonatkoztatási rendszerben dolgozunk, nem a színpadhoz rögzítettben, akkor úgy választhatjuk a rendszert, hogy a gördülő gömb középpontja legyen az origó.
görbe természetes paraméterezése. Ha az eszközhöz rögzített vonatkoztatási rendszerben dolgozunk, nem a színpadhoz rögzítettben, akkor úgy választhatjuk a rendszert, hogy a gördülő gömb középpontja legyen az origó.
Az eszköz számára a sínek halmazát a következőképpen konstruáljuk meg. Először egy, a gördülő gömböt érintő 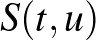 vonalkázott felületet konstruálunk, ami olyan vonalakból áll, amelyek merőlegesek mind
vonalkázott felületet konstruálunk, ami olyan vonalakból áll, amelyek merőlegesek mind 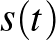 -re (a gömb centrumából a felszínére mutató vektor), mind
-re (a gömb centrumából a felszínére mutató vektor), mind 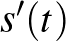 -re, ahol
-re, ahol 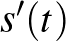 az
az 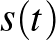 görbe első deriváltja (sebesség), és hasonlóképpen jelöljük a második deriváltat (gyorsulás). Azaz minden rögzített
görbe első deriváltja (sebesség), és hasonlóképpen jelöljük a második deriváltat (gyorsulás). Azaz minden rögzített  esetén
esetén 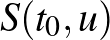 a következő egyenes:
a következő egyenes:
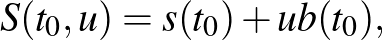 |
(1) |
ahol 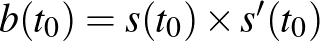 egy egységvektor. Felhasználva, hogy
egy egységvektor. Felhasználva, hogy 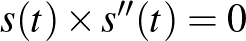 , direkt számolás mutatja, hogy az
, direkt számolás mutatja, hogy az 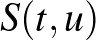 felület normálisa nem függ
felület normálisa nem függ 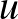 -tól. Ebből következik, hogy
-tól. Ebből következik, hogy 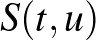 Gauss-görbülete 0, így
Gauss-görbülete 0, így 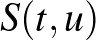 fejleszthető felület ([4], 91. old.).
fejleszthető felület ([4], 91. old.).
Ha  egy elegendően szép görbe, megcsonkítva az
egy elegendően szép görbe, megcsonkítva az 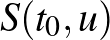 egyeneseket, ahol ezek metszik a
egyeneseket, ahol ezek metszik a  más pontjaiból jövő egyeneseket, egy
más pontjaiból jövő egyeneseket, egy 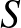 zárt felületet kapunk. Az 5. ábrán mutatott példában, a teniszlabdagörbe által generált zárt felület a gömbicsavartkúp (lásd 6/a. ábra). Egy zárt felület jól funkcionál egy szilárd objektum, mint a gömbicsavartkúp, határaként. Az akrobatikus eszköz számára az
zárt felületet kapunk. Az 5. ábrán mutatott példában, a teniszlabdagörbe által generált zárt felület a gömbicsavartkúp (lásd 6/a. ábra). Egy zárt felület jól funkcionál egy szilárd objektum, mint a gömbicsavartkúp, határaként. Az akrobatikus eszköz számára az 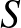 vonalkázott felületet helyettesíthetjük egy-dimenziós sínek egy
vonalkázott felületet helyettesíthetjük egy-dimenziós sínek egy 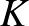 halmazával, amely ugyanilyen módon gördül
halmazával, amely ugyanilyen módon gördül  mentén. A
mentén. A 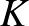 halmaznak vehetjük az
halmaznak vehetjük az 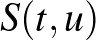 felület önmagával vett metszéspontjainak halmazát. A 6/a. ábrán ezek a gömbicsavartkúp félkörei. A cikk-cakk-gördülő hurkai a
felület önmagával vett metszéspontjainak halmazát. A 6/a. ábrán ezek a gömbicsavartkúp félkörei. A cikk-cakk-gördülő hurkai a  mentén gördülő síneknek másik halmaza.
mentén gördülő síneknek másik halmaza.
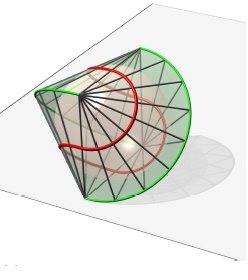
6/a. ábra
Általában 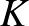 -ra az a megszorítás, hogy minden
-ra az a megszorítás, hogy minden 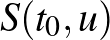 vonal esetén, a
vonal esetén, a 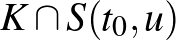 halmaz tartalmazzon egy pontot a
halmaz tartalmazzon egy pontot a 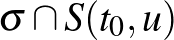 valamelyik oldalán. Ez biztosítja, hogy az eszköz ne boruljon fel a gördülő gömb centrumát és az
valamelyik oldalán. Ez biztosítja, hogy az eszköz ne boruljon fel a gördülő gömb centrumát és az 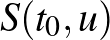 egyenest tartalmazó síkban.
egyenest tartalmazó síkban.
Eszközünk konstrukciójához szükségünk van még olyan extra struktúra hozzáadásához, amely összeköti a két félköríves sínt. A 6/b. ábrán ez a vonalkázott felület négy vonala, amely egy négyzetet alkot.
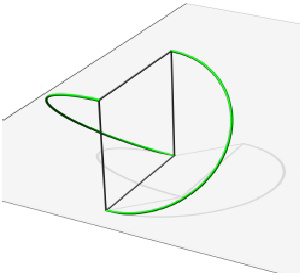
6/b. ábra
A teljes méretű fizikai eszköz esetén ezek a vonalak nem szükségesek. A 2. ábrán ezeket azok a csatlakozó ívek helyettesítik, amelyek az eszköz közepe felé görbülnek. Ezek megkönnyítik az akrobatának, hogy megkapaszkodjon, és megakadályozzák, hogy megragadjon egy rudat, amely a padlót érintve balesetet okozhat.
Milyen nagy legyen a porond?
Marco kérdésének a megválaszolásához meg kell értenünk a színpad síkján történő mozgást az eszköz gurulásakor. Azt akarjuk tudni, hogy a 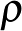 görbe korlátos-e? Mivel a
görbe korlátos-e? Mivel a  görbe zárt, ehhez meg kell értenünk az eszköz helyezetében és irányában fellépő különbségeket, miközben egyszer végiggördül
görbe zárt, ehhez meg kell értenünk az eszköz helyezetében és irányában fellépő különbségeket, miközben egyszer végiggördül  -n. A síknak ezt az izometriáját
-n. A síknak ezt az izometriáját  holonómiájának hívjuk és
holonómiájának hívjuk és 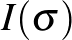 -val jelöljük.
-val jelöljük.
2. lemma. A 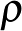 görbe akkor és csak akkor nem korlátos, ha az
görbe akkor és csak akkor nem korlátos, ha az 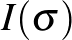 holonómia egy nemzérus vektor általi eltolás.
holonómia egy nemzérus vektor általi eltolás.
Bizonyítás: Először tegyük fel, hogy 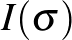 egy transzláció. Ekkor az eszköz ismétlődő gördülése
egy transzláció. Ekkor az eszköz ismétlődő gördülése  mentén megismétli a transzlációt, így az eszköz végül eléri akármilyen porond szélét. Másrészről, ha
mentén megismétli a transzlációt, így az eszköz végül eléri akármilyen porond szélét. Másrészről, ha 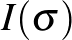 rotáció, akkor bár a
rotáció, akkor bár a 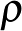 út soha nem tér vissza ugyanabba a helyzetbe és irányba, mint a mozgás kezdetén, nem kerülhet távolabb a forgás centrumától, mint a
út soha nem tér vissza ugyanabba a helyzetbe és irányba, mint a mozgás kezdetén, nem kerülhet távolabb a forgás centrumától, mint a  menti első mozgás során. Így egy véges sugarú porond tartalmazni fogja
menti első mozgás során. Így egy véges sugarú porond tartalmazni fogja 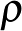 -t.
-t. 
Így Marco kérdésének a megválaszolásához meg kell értenünk a kapcsolatot a  görbe és a között a szög között, amellyel az eszköz elfordul, mialatt
görbe és a között a szög között, amellyel az eszköz elfordul, mialatt  mentén gördül.
mentén gördül.
3. tétel. Az eszköz elfordulási szöge, mialatt egyszer végiggördül a  egyszerű zárt görbén,
egyszerű zárt görbén,  és a gömb
és a gömb  által határolt valamelyik komponensének felszíne közötti különbség.
által határolt valamelyik komponensének felszíne közötti különbség.
Megjegyzés: A gömb felszíne 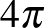 . A tételben szereplő két különbség előjeltől eltekintve megegyezik. A bizonyítás során a Gauss-Bonnet tételt alkalmazva megmutatjuk, hogy a tételben szereplő felszín különbség
. A tételben szereplő két különbség előjeltől eltekintve megegyezik. A bizonyítás során a Gauss-Bonnet tételt alkalmazva megmutatjuk, hogy a tételben szereplő felszín különbség  teljes geodetikus görbületével egyenlő. Ez megegyezik a
teljes geodetikus görbületével egyenlő. Ez megegyezik a 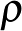 egy periódus alatti teljes geodetikus görbületével, amely akkor és csak akkor 0, ha a holonómia transzláció.
egy periódus alatti teljes geodetikus görbületével, amely akkor és csak akkor 0, ha a holonómia transzláció.
Bizonyítás: Miközben a gördülő gömb gurul a síkon, ezzel együtt gurul a vonalkázott felületet is. Így síkbeli egyenesek 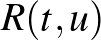 egy-paraméteres családja jön létre, amelyet az
egy-paraméteres családja jön létre, amelyet az 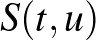 egyenesekből kapunk, amikor azok a síkot érintik. Például, ha
egyenesekből kapunk, amikor azok a síkot érintik. Például, ha  egy körív, akkor az
egy körív, akkor az 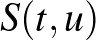 megfelelő részhalmaza része egy kúpnak. Az
megfelelő részhalmaza része egy kúpnak. Az 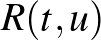 egy-paraméteres család megfelelő részhalmaza egy körszelet (lásd 7. ábra).
egy-paraméteres család megfelelő részhalmaza egy körszelet (lásd 7. ábra).
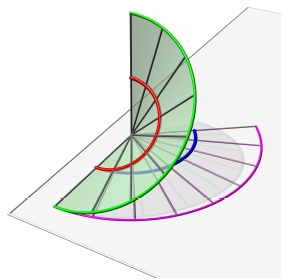
7. ábra
Ekkor világos, hogy 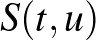 izometrikus
izometrikus 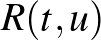 -val, és ez általánosan is igaz: a fejleszthető felület izometrikus a síkkal ([4]).
-val, és ez általánosan is igaz: a fejleszthető felület izometrikus a síkkal ([4]).
Legyen 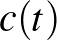 egy sima természetes paraméterezésű görbe az
egy sima természetes paraméterezésű görbe az  tér
tér 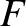 felületén. Legyen
felületén. Legyen 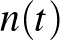 normális
normális 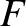 -hez
-hez 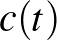 -ben. Ekkor
-ben. Ekkor  és
és 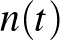 merőlegesek és így
merőlegesek és így 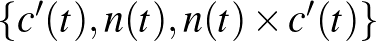
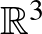 ortonormált bázisát alkotja. Így
ortonormált bázisát alkotja. Így 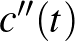 -t felírhatjuk, mint
-t felírhatjuk, mint  ,
, 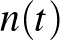 és
és 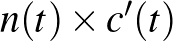 lineáris kombinációját. Sőt,
lineáris kombinációját. Sőt, 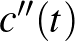 merőleges
merőleges  -re mivel
-re mivel 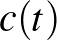 természetes paraméterezésű. Így
természetes paraméterezésű. Így
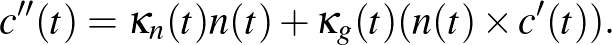 |
(2) |
Itt 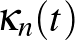 a normál görbülete,
a normál görbülete, 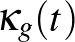 a geodetikus görbülete
a geodetikus görbülete  -nek a
-nek a 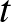 pillanatban. A geodetikus görbület belső, azaz invariáns a felület izometriáival szemben. Továbbá,
pillanatban. A geodetikus görbület belső, azaz invariáns a felület izometriáival szemben. Továbbá, 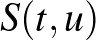 -n az
-n az 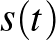 geodetikus görbülete megegyezik
geodetikus görbülete megegyezik 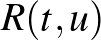 -n az
-n az 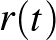 geodetikus görbületével. Mivel
geodetikus görbületével. Mivel  egyszerű, a gördülő gömböt két részre bontja. Legyen
egyszerű, a gördülő gömböt két részre bontja. Legyen 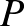 a
a  bal oldali,
bal oldali, 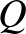 a jobb oldali része. Alkalmazzuk a Gauss-Bonnet tételt
a jobb oldali része. Alkalmazzuk a Gauss-Bonnet tételt 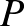 -re:
-re:
A második integrál összege a 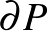 sima darabjai mentén vett integráloknak plusz azoknak a szögeknek az összege, amelyeket a sima darabok zárnak be a találkozásuknál. A
sima darabjai mentén vett integráloknak plusz azoknak a szögeknek az összege, amelyeket a sima darabok zárnak be a találkozásuknál. A 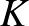 Gauss görbület
Gauss görbület  , a
, a 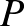 felület
felület 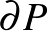 határa
határa  , a
, a 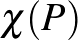 Euler karakterisztika
Euler karakterisztika 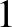 . Így átrendezve (3)-at azt kapjuk:
. Így átrendezve (3)-at azt kapjuk:
Mivel  geodetikus görbülete
geodetikus görbülete 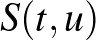 -n egyenlő
-n egyenlő 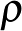 geodetikus görbületével
geodetikus görbületével 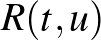 -n, tekinthetjük
-n, tekinthetjük 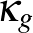 -t
-t 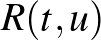 geodetikus görbületének.
geodetikus görbületének. 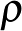 síkgörbe, ezért normál görbülete 0. Így
síkgörbe, ezért normál görbülete 0. Így 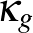 éppen a
éppen a 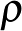 síkgörbe előjeles görbülete. Ismét, az integrál megkapható, mint a sima darabok mentén vett integrálok összege, plusz azon szögek összege, amelyeket a sima darabok a sarkoknál bezárnak. Tetszőleges saroknál a szögek összege ugyanaz a síkon és a gömbön. Így a (4) egyenlet jobb oldala a
síkgörbe előjeles görbülete. Ismét, az integrál megkapható, mint a sima darabok mentén vett integrálok összege, plusz azon szögek összege, amelyeket a sima darabok a sarkoknál bezárnak. Tetszőleges saroknál a szögek összege ugyanaz a síkon és a gömbön. Így a (4) egyenlet jobb oldala a 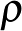 görbe irányának teljes változását adja, amint egyszer körbefutunk
görbe irányának teljes változását adja, amint egyszer körbefutunk  -n. Ebből következik a 3. tétel.
-n. Ebből következik a 3. tétel. 
A 3. tételt alkalmazva, a fordulási szög 0, ha a 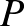 felszíne
felszíne  , azaz pontosan a gördülő gömb felszínének a fele. A fordulási szög nem lehet
, azaz pontosan a gördülő gömb felszínének a fele. A fordulási szög nem lehet  valamely más egész többszöröse, hiszen ekkor a
valamely más egész többszöröse, hiszen ekkor a 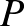 vagy a
vagy a 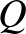 felszíne kisebb vagy egyenlő mint 0. Ez lehetetlen anélkül, hogy
felszíne kisebb vagy egyenlő mint 0. Ez lehetetlen anélkül, hogy  vagy önmagát metszené vagy triviális lenne.
vagy önmagát metszené vagy triviális lenne.
Ennélfogva:
4. következmény: Egy gördülő eszköz korlátlan porondot kíván akkor és csak akkor, ha a  görbe két egyforma területű részre bontja a gördülő gömb felszínét.
görbe két egyforma területű részre bontja a gördülő gömb felszínét.
Ez történik a cikk-cakk-gördülő eszköz esetében, ahol  a teniszlabdagörbe (lásd 5. ábra). A deformált teniszlabdagörbék egy-paraméteres családjába négy félkörből álló görbék tartoznak, amelyek végpontjai a gördülő gömb egyik főkörét egy téglalap csúcsaiban metszik (lásd 8. bal oldali ábra).
a teniszlabdagörbe (lásd 5. ábra). A deformált teniszlabdagörbék egy-paraméteres családjába négy félkörből álló görbék tartoznak, amelyek végpontjai a gördülő gömb egyik főkörét egy téglalap csúcsaiban metszik (lásd 8. bal oldali ábra).
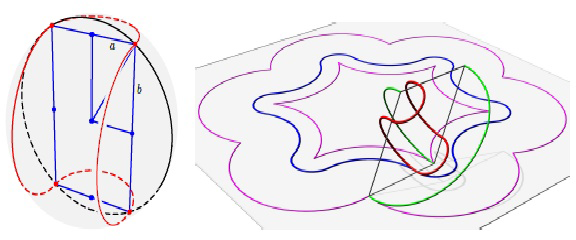
8. ábra
Ekkor két különböző, 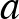 ,
, 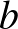 sugarú félkörünk van úgy, hogy
sugarú félkörünk van úgy, hogy 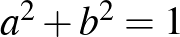 . Így a gömb két komponensének felületét a következőképpen kapjuk: A gömb
. Így a gömb két komponensének felületét a következőképpen kapjuk: A gömb 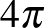 felszíne a következőkből áll: két gömbsüvegből, amelyek határa az
felszíne a következőkből áll: két gömbsüvegből, amelyek határa az 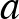 sugarú körvonal, két gömbsüvegből, amelyek határa a
sugarú körvonal, két gömbsüvegből, amelyek határa a 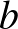 sugarú körvonal és a maradékból, ami két görbült téglalap. Az
sugarú körvonal és a maradékból, ami két görbült téglalap. Az 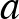 sugarú körvonal által határolt gömbsüveg felszíne:
sugarú körvonal által határolt gömbsüveg felszíne: 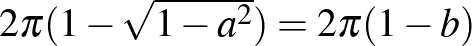 . Ezért a két görbült téglalap felszíne:
. Ezért a két görbült téglalap felszíne:
 |
(5) |
Így az 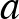 sugarú körvonal által határolt gömbsüveget tartalmazó komponens felszíne:
sugarú körvonal által határolt gömbsüveget tartalmazó komponens felszíne:
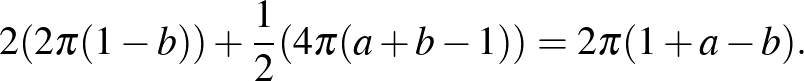 |
(6) |
Ezért az eszköz elfordulási szöge 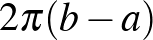 . Megadva egy kívánt elfordulási szöget,
. Megadva egy kívánt elfordulási szöget, 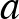 -ra és
-ra és 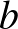 -re megoldhatjuk az egyenletet. Például ha
-re megoldhatjuk az egyenletet. Például ha 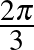 elfordulási szöget akarunk, akkor
elfordulási szöget akarunk, akkor 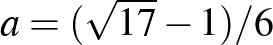 ,
, 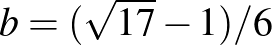 . A 8. jobb oldali ábra egy ilyen paraméterű eszközt és mozgását mutatja. Ez az eszköz azonban nem teljesíti azt a feltevésünket, hogy tömegközéppontja a gördülő gömb centruma. A következő tétel egy szimmetrián alapuló kritériumot ad arra, hogy a végső fizikai eszköz tömegközéppontja az origó legyen:
. A 8. jobb oldali ábra egy ilyen paraméterű eszközt és mozgását mutatja. Ez az eszköz azonban nem teljesíti azt a feltevésünket, hogy tömegközéppontja a gördülő gömb centruma. A következő tétel egy szimmetrián alapuló kritériumot ad arra, hogy a végső fizikai eszköz tömegközéppontja az origó legyen:
5. tétel: Ha az eszköz szimmetriacsoportja csak a gördülő gömb  origóját hagyja pontonként fixen, akkor az eszköz tömegközéppontja
origóját hagyja pontonként fixen, akkor az eszköz tömegközéppontja  .
.
Bizonyítás: Definició szerint egy objektumot a szimmetriacsoportjának minden eleme fixen hagyja. Így az objektum tömegközéppontja is fix. A tétel feltétele mellett a tömegközéppontnak az  -ban kell lennie.
-ban kell lennie. 
Egy korlátos háromdimenziós objektum szimmetriáinak talán legismertebb jelölési rendszere a Conway-Thurston jelölés ([1]). Ez a jelölés az 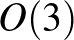 ortogonális csoport véges részcsoportjait írja le,
ortogonális csoport véges részcsoportjait írja le, 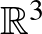 azon izometriáit, amelyek az origót fixen hagyják. A 9. ábra néhány példát mutat szimmetrikus objektumokra a Conway-Thurston jelölésükkel.
azon izometriáit, amelyek az origót fixen hagyják. A 9. ábra néhány példát mutat szimmetrikus objektumokra a Conway-Thurston jelölésükkel.
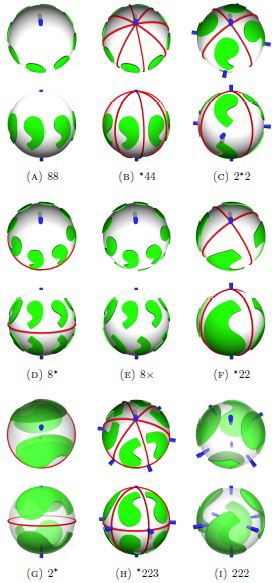
9. ábra
Minden objektumot felül- és oldalnézetből látunk. A forgatások fixpontjai kékkel vannak jelölve, a tükrözéssel szemben fix síkok pirossal. A jelölés egész számok egy sorozata, ami tartalmazhatja a  vagy a
vagy a 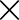 szimbólumot. Ha nem tartalmazza ezeket a szimbólumokat, akkor egy
szimbólumot. Ha nem tartalmazza ezeket a szimbólumokat, akkor egy 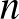 szám azt mutatja, hogy a gömbnek van egy pontja, amely fix az
szám azt mutatja, hogy a gömbnek van egy pontja, amely fix az 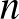 -szeri (
-szeri ( szögű) forgatással szemben. A 9 (A) ábrán két különböző pont van, amely fix a
szögű) forgatással szemben. A 9 (A) ábrán két különböző pont van, amely fix a 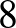 -szoros forgatással szemben, így a jelölés
-szoros forgatással szemben, így a jelölés 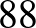 . A
. A  szimbólum jelenléte azt mutatja, hogy létezik tükrözéssel szemben fix szimmetriasík. Egy
szimbólum jelenléte azt mutatja, hogy létezik tükrözéssel szemben fix szimmetriasík. Egy 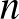 szám a
szám a  jel után azt jelenti, hogy létezik egy pont a gömbön, amelyen keresztül
jel után azt jelenti, hogy létezik egy pont a gömbön, amelyen keresztül 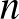 különböző tükrözéssel szemben fix sík halad. A 9 (B) ábrán két különböző pont létezik, amelyeken keresztül
különböző tükrözéssel szemben fix sík halad. A 9 (B) ábrán két különböző pont létezik, amelyeken keresztül 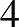 szimmetriatükör-sík halad, így a jelölés
szimmetriatükör-sík halad, így a jelölés 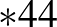 . Egy szám a
. Egy szám a  szimbólum előtt azt jelenti, hogy létezik egy pont a korábban leírt forgatási szimmetriával. Végezetül, egy tükrözéstől különböző irányításváltó szimmetria létezését a
szimbólum előtt azt jelenti, hogy létezik egy pont a korábban leírt forgatási szimmetriával. Végezetül, egy tükrözéstől különböző irányításváltó szimmetria létezését a 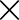 jelöli. A 9 (E) ábrán van egy pont, amely fix a
jelöli. A 9 (E) ábrán van egy pont, amely fix a 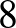 -szoros forgatással szemben, és létezik egy olyan szimmetria, amely egy forgatás és egy tükrözés kompozíciója. A gömbi szimmetriatípusok teljes listáját, és ennek a bizonyítását megtaláljuk ([1])-ben. Azok a szimmetriatípusok, amelyeknek több fixpontjuk van, mint az origó, az
-szoros forgatással szemben, és létezik egy olyan szimmetria, amely egy forgatás és egy tükrözés kompozíciója. A gömbi szimmetriatípusok teljes listáját, és ennek a bizonyítását megtaláljuk ([1])-ben. Azok a szimmetriatípusok, amelyeknek több fixpontjuk van, mint az origó, az 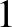 ,
, 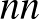 és a
és a 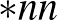 ,
, 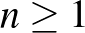 . Példaként, az eredeti cikk-cakk-gördülő eszköz szimmetriatípusa
. Példaként, az eredeti cikk-cakk-gördülő eszköz szimmetriatípusa  (lásd 9 (C) ábra), így a tömegközéppontja az origóban van. A módosított teniszlabdagörbéhez tartozó cikk-cakk-gördülő eszköz szimmetriatípusa
(lásd 9 (C) ábra), így a tömegközéppontja az origóban van. A módosított teniszlabdagörbéhez tartozó cikk-cakk-gördülő eszköz szimmetriatípusa 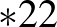 (lásd 9 (F) ábra), így nem lehet a tömegközéppontja az origó. A következő tétel azt mutatja, hogy más egyszerű zárt görbe esetén is lehetetlen az, hogy nem egyenlő felületű részekre osztja a gömböt de a tömegközéppont az origó.
(lásd 9 (F) ábra), így nem lehet a tömegközéppontja az origó. A következő tétel azt mutatja, hogy más egyszerű zárt görbe esetén is lehetetlen az, hogy nem egyenlő felületű részekre osztja a gömböt de a tömegközéppont az origó.
6 tétel: Tegyük fel, hogy  egy szakaszonként sima egyszerű zárt görbe a gömbön. Ha
egy szakaszonként sima egyszerű zárt görbe a gömbön. Ha  a gömböt két nem izometrikus részre bontja, akkor
a gömböt két nem izometrikus részre bontja, akkor 
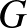 szimmetriacsoportja nemcsak a gömb origóját rögzíti pontonként.
szimmetriacsoportja nemcsak a gömb origóját rögzíti pontonként.
Bizonyítás: Legyen 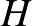 a
a 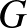 irányítástartó részcsoportja. Először tegyük fel, hogy
irányítástartó részcsoportja. Először tegyük fel, hogy 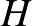 triviális. Ha
triviális. Ha 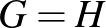 akkor
akkor 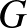 mindent fixen hagy és készen vagyunk. Egyébként,
mindent fixen hagy és készen vagyunk. Egyébként, 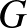 -t egy másodrendű elem generálja: vagy egy tükrözés vagy egy antipoláris leképezés. Az első esetben (szimmetriatípusa
-t egy másodrendű elem generálja: vagy egy tükrözés vagy egy antipoláris leképezés. Az első esetben (szimmetriatípusa  )
) 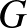 fixen hagyja a tükrözés szimmetriasíkját, így készen vagyunk. A második esetben (szimmetriatípusa
fixen hagyja a tükrözés szimmetriasíkját, így készen vagyunk. A második esetben (szimmetriatípusa  ) az antipoláris leképezés felcseréli a
) az antipoláris leképezés felcseréli a  által határolt két kiegészítő komponenst. Így ezek izomorfak, ellentétben a feltevéssel.
által határolt két kiegészítő komponenst. Így ezek izomorfak, ellentétben a feltevéssel.
Segédállítás: Legyen 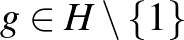 . Ekkor
. Ekkor  egy rotáció. A
egy rotáció. A  hurok nem tartalmazza
hurok nem tartalmazza  fixpontjait.
fixpontjait.
Bizonyítás: Euler tétele szerint a gömb minden nemtriviális irányítástartó izometriája rotáció. Indirekt tegyük fel, hogy 
 egy fixpontja. Mivel
egy fixpontja. Mivel  egyszerű, így
egyszerű, így 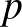 egy kis környezetét két komponensre bontja. De
egy kis környezetét két komponensre bontja. De  nem cserélheti fel a két komponenst, mivel a
nem cserélheti fel a két komponenst, mivel a  által határolt kiegészítő részek nem izometrikusak.
által határolt kiegészítő részek nem izometrikusak. 
Következőnek tegyük fel, hogy 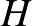 véges és nemtriviális. Megmutatjuk, hogy
véges és nemtriviális. Megmutatjuk, hogy 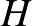 ciklikus. A Segédállítás miatt és mivel
ciklikus. A Segédállítás miatt és mivel 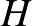 véges,
véges, 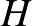 hatása a
hatása a  hurkon szabad, és sehol sem folytonos. Ebből következik, hogy a
hurkon szabad, és sehol sem folytonos. Ebből következik, hogy a 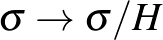 egy fedő leképezés. Az egyetlen tér, amely a kört lefedi a kör. A
egy fedő leképezés. Az egyetlen tér, amely a kört lefedi a kör. A 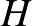 csoport ekkor a kör fundamentális csoportjának egy faktorcsoportja, így ciklikus. Ennélfogva a
csoport ekkor a kör fundamentális csoportjának egy faktorcsoportja, így ciklikus. Ennélfogva a 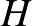 csoport egy tengelyt pontonként fixen hagy, és így fixen hagy a gömbön egy antipoláris pontpárt,
csoport egy tengelyt pontonként fixen hagy, és így fixen hagy a gömbön egy antipoláris pontpárt, 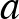 -t és
-t és  -t . A Segédállítás miatt
-t . A Segédállítás miatt  sem
sem 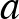 -t sem
-t sem  -t nem tartalmazza. Megmutatjuk, hogy
-t nem tartalmazza. Megmutatjuk, hogy  szeparálja
szeparálja 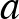 -t és
-t és  -t. Ehhez tekintsük az
-t. Ehhez tekintsük az 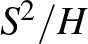 hányadosteret. Ez ismét egy kétdimenziós gömbfelület két speciális ponttal,
hányadosteret. Ez ismét egy kétdimenziós gömbfelület két speciális ponttal, 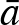 és
és 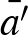 -vel. Ha
-vel. Ha 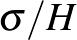 szeparálja
szeparálja 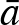 -t
-t 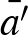 -től, akkor készen vagyunk. Ha nem, akkor válasszunk egy
-től, akkor készen vagyunk. Ha nem, akkor válasszunk egy 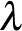 utat
utat 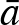 -ból
-ból 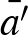 -be, ami nem metszi
-be, ami nem metszi 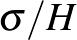 -t. A
-t. A 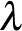 ősképe szétvágja a gömböt legalább két komponensre, amelyek mindegyike metszi
ősképe szétvágja a gömböt legalább két komponensre, amelyek mindegyike metszi  -t. Ez ellentmond annak, hogy
-t. Ez ellentmond annak, hogy  összefüggő.
összefüggő.
Ha 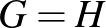 (szimmetriatípusa
(szimmetriatípusa 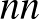 ) akkor készen vagyunk. Egyébként,
) akkor készen vagyunk. Egyébként, 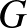 -t megkapjuk
-t megkapjuk 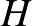 -ból, ha hozzáadunk egyetlen irányításváltó izometriát, és vesszük a csoport lezártját. Az új elemnek a tengelyt mint halmazt fixen kell hagynia, sőt a tükrözés általi konjugálás új forgatásokat hoz létre. Az új elem sem cserélheti fel
-ból, ha hozzáadunk egyetlen irányításváltó izometriát, és vesszük a csoport lezártját. Az új elemnek a tengelyt mint halmazt fixen kell hagynia, sőt a tükrözés általi konjugálás új forgatásokat hoz létre. Az új elem sem cserélheti fel 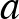 -t és
-t és  -t, mivel azok a
-t, mivel azok a  két nem izometrikus kiegészítő komponensére esnek. Így
két nem izometrikus kiegészítő komponensére esnek. Így 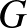 ismét fixen hagyja a tengelyt. (Az új szimmetriatípus
ismét fixen hagyja a tengelyt. (Az új szimmetriatípus 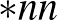 . Mivel
. Mivel ![]() és
és  nem felcserélhető, ez kizárja a
nem felcserélhető, ez kizárja a 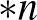 és a
és a  típusokat).
típusokat).
Végül tegyük fel, hogy 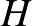 végtelen. Ekkor
végtelen. Ekkor 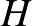 zárt végtelen részcsoportja
zárt végtelen részcsoportja 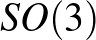 -nak. Így vagy a teljes
-nak. Így vagy a teljes 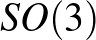 csoport, vagy izomorf
csoport, vagy izomorf 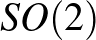 -vel. Az első lehetetlen, mivel egy szakaszonként sima görbe nem metszheti a gömb minden pontját. Így
-vel. Az első lehetetlen, mivel egy szakaszonként sima görbe nem metszheti a gömb minden pontját. Így 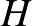 izomorf
izomorf 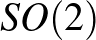 -vel és
-vel és  egy körvonal. Mivel
egy körvonal. Mivel  nem egyforma részekre bontja a gömböt, így nem főkör. Így
nem egyforma részekre bontja a gömböt, így nem főkör. Így 
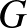 szimmetriacsoportja fixen hagyja
szimmetriacsoportja fixen hagyja  tengelyét.
tengelyét. 
Ha általánosítjuk a konstrukciónkat, megengedve többszörös hurkokat, kielégíthetjük az 5. és 6. tételeket. Az ötlet, az, hogy a  görbét a gördülő gömbbe ágyazott
görbét a gördülő gömbbe ágyazott  gráffal helyettesítjük. A
gráffal helyettesítjük. A  gráf változatos hurkokat tartalmazhat, amelyek egyenletlenül osztják fel a gömböt, mégis a teljes gráf (és így az eszköz) szimmetriatípusa teljesíti az 5. tételt. Két ilyen eszközt mutatunk be:
gráf változatos hurkokat tartalmazhat, amelyek egyenletlenül osztják fel a gömböt, mégis a teljes gráf (és így az eszköz) szimmetriatípusa teljesíti az 5. tételt. Két ilyen eszközt mutatunk be:
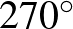 -os forduló eszköz: Ez az eszköz mozoghat egyenes vonalon, mint a német kerék, de
-os forduló eszköz: Ez az eszköz mozoghat egyenes vonalon, mint a német kerék, de 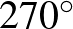 -os elfordulást is megenged, innen kapta a nevét. Ezért a
-os elfordulást is megenged, innen kapta a nevét. Ezért a  gráf tartalmaz egy főkört és két kisebb kört olyan sugárral, amely lehetővé teszi a
gráf tartalmaz egy főkört és két kisebb kört olyan sugárral, amely lehetővé teszi a 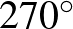 -os elfordulást. A 3. tétel szerint a gömbsüveg felülete mindkét kis kör esetén
-os elfordulást. A 3. tétel szerint a gömbsüveg felülete mindkét kis kör esetén 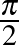 . Ebből adódik, hogy a kis kör sugara
. Ebből adódik, hogy a kis kör sugara 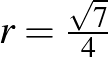 (lásd a 10/a. ábrát).
(lásd a 10/a. ábrát).

10/a. ábra
Az eszköz szimmetriája 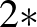 (9 (G) ábra). Követve a korábban leírt konstrukciót, az eszköz modellje a 10/b. ábrán látható. Az eszköz sínpárja két, az ábrán zölddel jelölt ellipszis.
(9 (G) ábra). Követve a korábban leírt konstrukciót, az eszköz modellje a 10/b. ábrán látható. Az eszköz sínpárja két, az ábrán zölddel jelölt ellipszis.
10/b. ábra
Ismét összekapcsoljuk a síneket bizonyos vonalakkal. Ezek a vonalak 10/b. ábrán a szürke paralelogrammát alkotják. A 10/c. ábrán az eszközzel megtehető utakat látjuk. A szemléltetett helyzetben, feltéve, hogy az eszköz távolodik tőlünk, folytathatja a gördülést egyenes vonalban, vagy 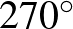 -kal elfordulhat balra. Ha így tesz, akkor visszatér az eredeti állapotban (annak a pontnak a tekintetében, ahol a gömb érinti a padlót), de elmozdult és megváltoztatta az irányát a padlón. Másik lehetőség, hogy fél fordulatot előre gurul és ott
-kal elfordulhat balra. Ha így tesz, akkor visszatér az eredeti állapotban (annak a pontnak a tekintetében, ahol a gömb érinti a padlót), de elmozdult és megváltoztatta az irányát a padlón. Másik lehetőség, hogy fél fordulatot előre gurul és ott 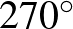 -kal elfordul jobbra. Ezek együttesen lehetővé teszik, hogy az eszköz többé-kevésbé mindenütt mozogjon végtelen porondon vagy elforduljon, és ezzel egy (elegendően nagy) korlátos területen maradjon.
-kal elfordul jobbra. Ezek együttesen lehetővé teszik, hogy az eszköz többé-kevésbé mindenütt mozogjon végtelen porondon vagy elforduljon, és ezzel egy (elegendően nagy) korlátos területen maradjon.
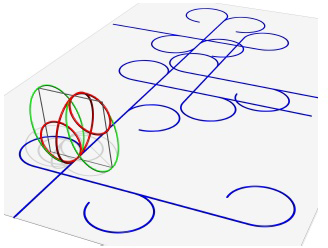
10/c. ábra
Három gyűrű eszköz: A következő eszköz a gördülő gömbbe ágyazható kör alakú hurokról tett megfigyelésen alapszik, amely 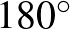 -os fordulatnak felel meg. Alkalmazva a 3. tételt, a körök által határolt gömbsüveg felülete
-os fordulatnak felel meg. Alkalmazva a 3. tételt, a körök által határolt gömbsüveg felülete 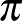 . Így a körök sugara
. Így a körök sugara 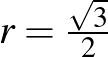 . Három ilyen kör pontosan elfér a gördülő gömb egy főköre körül (lásd 11/a. ábra).
. Három ilyen kör pontosan elfér a gördülő gömb egy főköre körül (lásd 11/a. ábra).
11/a. ábra
A három kör érinti egymást, az eszköz szimmetriatípusa  (lásd 9 (H) ábra). A korábban leírt módon generálva síneket ehhez az eszközhöz, megkapjuk a 11/b. ábrán mutatott modellt. A síneket ismét zölddel jelöltük. Ismét vonalakat adunk az eszközhöz a sínek összekapcsolására. Ezek végpontjai a három kör, mint alapkör által meghatározott kúp csúcsai. Itt a vonalak sokkal nagyobbá teszik az eszközt, mint csupán a sínek. Mint korábban, a teljes eszköz megépítéséhez ezek a vonalak nem szükségesek.
(lásd 9 (H) ábra). A korábban leírt módon generálva síneket ehhez az eszközhöz, megkapjuk a 11/b. ábrán mutatott modellt. A síneket ismét zölddel jelöltük. Ismét vonalakat adunk az eszközhöz a sínek összekapcsolására. Ezek végpontjai a három kör, mint alapkör által meghatározott kúp csúcsai. Itt a vonalak sokkal nagyobbá teszik az eszközt, mint csupán a sínek. Mint korábban, a teljes eszköz megépítéséhez ezek a vonalak nem szükségesek.
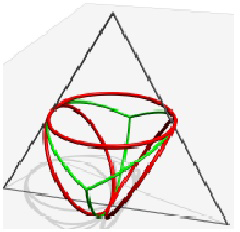
11/b. ábra
A kúpok csúcsait ki lehet cserélni a kúpon áthaladó kör keresztmetszetű sínekre, amelyek párhuzamosak  köreivel. Félpályát gurulva a körök egyike mentén a sínpálya egyik csúcsából a másikba, a porondon egy negyed körívű forgás történik. A jobbra és balra történő fordulások váltakozásával ez az eszköz közelíti egy cikk-cakk-gördülő eszköz mozgását, bár az artista természetesen más utat is választhat a sínpálya bármely csúcsában. Az eszköz néhány lehetséges elmozdulását a 11/c. ábra mutatja.
köreivel. Félpályát gurulva a körök egyike mentén a sínpálya egyik csúcsából a másikba, a porondon egy negyed körívű forgás történik. A jobbra és balra történő fordulások váltakozásával ez az eszköz közelíti egy cikk-cakk-gördülő eszköz mozgását, bár az artista természetesen más utat is választhat a sínpálya bármely csúcsában. Az eszköz néhány lehetséges elmozdulását a 11/c. ábra mutatja.

11/c. ábra
Irodalomjegyzék
- [1] J. H. Conway, H. Burgiel and C. Goodman-Strauss, The symmtries of things, A K Peters, Ltd., Wellesley, MA, 2008.
[2] H. Segerman, Rolling Acrobatic Apparatus, Notices in AMS, 68, no. 7 (2021), 1106–1118.
[3] I. Stewart, Cone with a twist, Scientific American 281, no. 4 (1999), 116–117.
[4] D. J. Struik, Lectures on classical differential geometry, Addison-Wesley Press, Inc., Cambridge, Mass., 1950.
Munkánkat a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal (NKFI) K132951 és az EFOP-3.6.1-16-2016-00022 projekt támogatta. A második projektet az Európai Unió és az Európai Szociális Alap finanszírozza.
Henry H. Segerman, Rolling Acrobatic Apparatus, Notices in AMS, 68, no. 7 (2021), 1106–1118. cikkét fordította, átdolgozta: Figula Ágota, Debreceni Egyetem, TTK Matematikai Intézet.
© H. Segerman. A cikk a szerző engedélyével jelenik meg.
© Marco Paoletti. Az 1.ábra az engedélyével jelenik meg.
© Toni Vighetto. A 2. ábra az engedélyével jelenik meg.