
John Forbes Nash (1928–2015)
Ismert, hogy Nash (Nash (1950a)) és (Nash (1951)) cikkeiben tanulmányozta elsőként az 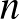 -személyes nemkooperatív játékelmélet – egyébként kézenfekvő – egyensúlyát, amelyet hamarosan róla neveztek el. De sokan még ma sem tudják, milyen rögös út vezetett el a definícióhoz és az egzisztenciatétel kimondásához. Ebben a rövid írásban az említett felfedezést a matematika alkalmazásai iránt érdeklődők számára vázolom (vö. Raussen–Skau 2015-ös interjúja John Nash-sel (Raussen, Skau (2015)), amely Nash 2015-ös Abel-díja alkalmából készült, és Nasar (Nasar (1998)) kiváló életrajza).1 Nash kiindulópontja Neumann 1928-as kétszemélyes nullaösszegű játékelméleti modellje volt (Neumann (1928)), pontosabban annak Neumann–Morgenstern 1944-es változata (Neumann, Morgenstern (1944)). (Furcsa, hogy hősünk még a 2015-ös interjújában is a következő történetileg téves állítást teszi: „Nem emlékszem pontosan, mikor történt, de Neumann és Morgenstern Princetonban találtak egy bizonyítást a kétszereplős játékok megoldására, ami egy speciális esete az én általános tételemnek
-személyes nemkooperatív játékelmélet – egyébként kézenfekvő – egyensúlyát, amelyet hamarosan róla neveztek el. De sokan még ma sem tudják, milyen rögös út vezetett el a definícióhoz és az egzisztenciatétel kimondásához. Ebben a rövid írásban az említett felfedezést a matematika alkalmazásai iránt érdeklődők számára vázolom (vö. Raussen–Skau 2015-ös interjúja John Nash-sel (Raussen, Skau (2015)), amely Nash 2015-ös Abel-díja alkalmából készült, és Nasar (Nasar (1998)) kiváló életrajza).1 Nash kiindulópontja Neumann 1928-as kétszemélyes nullaösszegű játékelméleti modellje volt (Neumann (1928)), pontosabban annak Neumann–Morgenstern 1944-es változata (Neumann, Morgenstern (1944)). (Furcsa, hogy hősünk még a 2015-ös interjújában is a következő történetileg téves állítást teszi: „Nem emlékszem pontosan, mikor történt, de Neumann és Morgenstern Princetonban találtak egy bizonyítást a kétszereplős játékok megoldására, ami egy speciális esete az én általános tételemnek 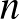 -szereplős játékokra.” A nevezett bizonyítást valójában Neumann már 1928-ban közölte.) A döntő lépés nem annyira az volt, hogy Nash a szereplők számát 2-ről
-szereplős játékokra.” A nevezett bizonyítást valójában Neumann már 1928-ban közölte.) A döntő lépés nem annyira az volt, hogy Nash a szereplők számát 2-ről 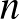 -re emelte, hanem az, hogy szakított a társasjátékokra jellemző, de nagyon megszorító nullaösszegűséggel. Ez az általánosítás viszont speciális esetben már (Cournot (1838))-ban megjelent, csak sem Neumann, sem Nash nem tudott róla.
-re emelte, hanem az, hogy szakított a társasjátékokra jellemző, de nagyon megszorító nullaösszegűséggel. Ez az általánosítás viszont speciális esetben már (Cournot (1838))-ban megjelent, csak sem Neumann, sem Nash nem tudott róla.
1. Cournot duopólium modellje
A többszemélyes stratégiai döntések közgazdasági elmélete felé az első lépést egy francia tudós, Cournot (Cournot (1838)) tette meg, amikor bevezette a duopólium fogalmát, és meghatározta az egyensúlyt. Emlékeztetőül: egy piacon két vállalat árusít azonos áron azonos terméket, amelynek ár–keresleti függvénye, 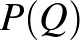 csökkenő. A két vállalat
csökkenő. A két vállalat 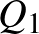 és
és 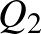 mennyiséget dob a piacra (értékük tetszőleges pozitív valós szám), és ennek összegeként adódik a piaci kínálat:
mennyiséget dob a piacra (értékük tetszőleges pozitív valós szám), és ennek összegeként adódik a piaci kínálat: 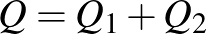 . Elhanyagolva a közösnek feltételezett egységköltséget, mindkét vállalat árbevétele, egyben profitja nemcsak saját, hanem a vetélytársa kínálatától is függ:
. Elhanyagolva a közösnek feltételezett egységköltséget, mindkét vállalat árbevétele, egyben profitja nemcsak saját, hanem a vetélytársa kínálatától is függ:
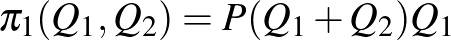 és
és 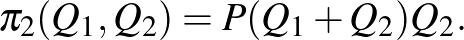
Hogyan lehet megfogalmazni a megfelelő piaci egyensúlyt? Egyensúlynak nevezünk egy olyan kínálatpárt, amelytől egyik vállalatnak sem érdemes egyedül eltérnie.
Cournot zseniális gondolata szerint mindkét vállalat adottnak veszi a másik kínálatát, és meghatározza saját profitjának feltételes maximumát. Folytonosan változtatva a másik kínálatát, megkapjuk a reakciófüggvényt:  és
és  . Képletben:
. Képletben:
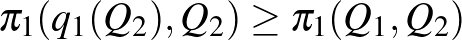 és
és 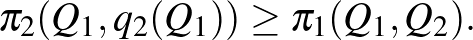
Egyszerű feltételek mellett létezik egy olyan, konzisztensnek nevezett kínálati pár: 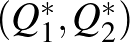 , amelyre
, amelyre
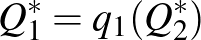 és
és 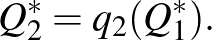
A reakciófüggvények nélkül is definiálható az egyensúly: minden 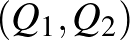 párra fennáll
párra fennáll
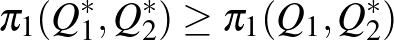 és
és 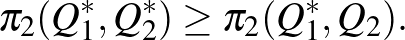
Hangsúlyozom, hogy a két vállalat nem kooperál egymással, pedig összejátszás esetén mindketten kínálhatnák a monopolista egyensúly felét, és megfelezhetnék a monopolista hasznot. Másképp szólva, létezhet olyan kínálatpár: 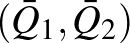 , amely mindkét félnek előnyösebb, mint az egyensúly, de összejátszás nélkül nem valósítható meg:
, amely mindkét félnek előnyösebb, mint az egyensúly, de összejátszás nélkül nem valósítható meg:
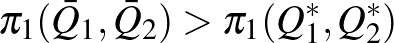 és
és 
Ha lineáris keresleti függvényt tételezünk föl, akkor az egyensúly explicite is meghatározható (lásd a későbbi 2. példát 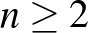 vállalat esetére).
vállalat esetére).
Cournot elképzelését vitatta egy neves francia matematikus (Bertrand (1883)): kínálati verseny helyett árversenyt modellezett, ezt azonban most figyelmen kívül hagyjuk. Jellemző, hogy a matematikai közgazdászok egyrészt folytatták (például Hotelling (1929)), másrészt hevesen bírálták Cournot elméletét. Schumpeter 1954-es elmélettörténete (Schumpeter (1954)) is érdemben tárgyalta, lásd 979–983. o., bár ő is kételkedett a Cournot-egyensúly széleskörű használhatóságában.2
2. Neumann modellje
Egészen más úton indult el Neumann 1928-as cikkében (magyarul Neumann (1965)). Ő egy elvontabb feladatot vizsgált. Legyen két játékos: 1. és 2., absztrakt stratégiai halmazuk rendre 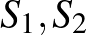 , tetszőleges stratégiája
, tetszőleges stratégiája 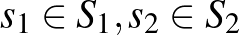 , és hasznosságfüggvénye
, és hasznosságfüggvénye 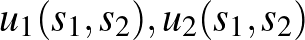 . Neumann-nál a stratégiák nemcsak valós számok lehetnek, mint Cournot-nál, hanem például a társasjátékokból ismert véges lépések sorozatai. A társasjátékok iránti heves érdeklődés magyarázza, hogy Neumann (1928) főleg nullaösszegű játékokat vizsgált:
. Neumann-nál a stratégiák nemcsak valós számok lehetnek, mint Cournot-nál, hanem például a társasjátékokból ismert véges lépések sorozatai. A társasjátékok iránti heves érdeklődés magyarázza, hogy Neumann (1928) főleg nullaösszegű játékokat vizsgált:
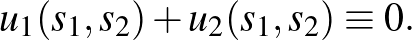
Történetünk szempontjából közömbös, hogy Neumann az egyensúlyt az ún. minmax-elvvel határozta meg, mi megelégszünk a Neumann-definícióval ekvivalens Cournot-egyensúly elvont felírásával:
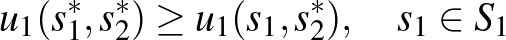 és
és 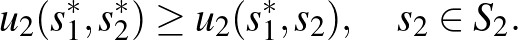
Már a legegyszerűbb esetben is problematikus az egyensúly létezése.
1. példa. Érmepárosítás. Két játékos egymástól függetlenül, egyidejűleg elhelyez 5–5 Ft-ot Fejre vagy Írásra. Ha azonos állásút választanak, az 1. nyer; ha különbözőt, akkor a 2., mindkétszer 5 Ft-ot.
| 2. játékos 1. játékos |
Fej | Írás |
| Fej | 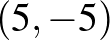 |
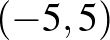 |
| Írás | 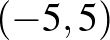 |
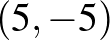 |
Könnyű belátni, hogy itt nem létezik egyensúly. Ahhoz, hogy létezzen egyensúly, általánosítani kell a játékot kevert stratégiákra. Válasszon az 1. és a 2. játékos egy-egy ![$p,q\in [0,1]$](/images/stories/latexuj/2021-03/2021-03-simonovitsanashrejtely/img30.png) valós számot, és
valós számot, és 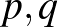 független valószínűséggel játssza az F-stratégiát, míg
független valószínűséggel játssza az F-stratégiát, míg 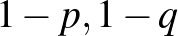 valószínűséggel játssza az Í-stratégiát. Ezzel mindkét játékos kiismerhetetlenné teszi viselkedését a másik előtt, matematikailag viszont ezáltal folytonossá válik az eredetileg diszkrét feladat. Ha elfogadjuk az ún. várható hasznosság elvét, akkor a két játékos hasznosságfüggvénye
valószínűséggel játssza az Í-stratégiát. Ezzel mindkét játékos kiismerhetetlenné teszi viselkedését a másik előtt, matematikailag viszont ezáltal folytonossá válik az eredetileg diszkrét feladat. Ha elfogadjuk az ún. várható hasznosság elvét, akkor a két játékos hasznosságfüggvénye
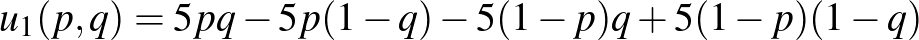 és
és 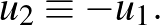
Ugyancsak könnyű igazolni, hogy ebben az általánosított játékban, ahol 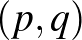 a stratégiapár, létezik egyensúly:
a stratégiapár, létezik egyensúly: 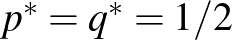 , és mindkét játékos nyeresége 0.
, és mindkét játékos nyeresége 0.
1. példa (folytatás). A továbbiak miatt érdemes felírni az 1. játékos legjobb válaszát a 2. választására:
![$\displaystyle \tilde p(q)=\begin{cases}0,&\text{ha }0\le q< 1/2;\\
\in [0,1],&\text{ha }q= 1/2;\\
1,&\text{ha }1/2<q\le 1.\end{cases}
$](/images/stories/latexuj/2021-03/2021-03-simonovitsanashrejtely/img37.png)
A második válaszfüggvény, 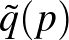 is hasonló. Figyelemre méltó, hogy a legjobb válasz – éppen az
is hasonló. Figyelemre méltó, hogy a legjobb válasz – éppen az 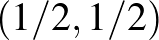 egyensúlyi pontban – halmazértékű. Emellett a két másik feltételes optimum sarokoptimum, amelyet a hagyományos kalkulus nehezen kezelt.
egyensúlyi pontban – halmazértékű. Emellett a két másik feltételes optimum sarokoptimum, amelyet a hagyományos kalkulus nehezen kezelt.
Komoly matematikai eredmény volt, hogy Neumann az egyensúly létezését általánosította kétszemélyes (véges) mátrixjátékokra, ahol az 1. játékos 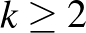 , a 2. játékos pedig
, a 2. játékos pedig  számú tiszta stratégia között választhat, és ezeket
számú tiszta stratégia között választhat, és ezeket
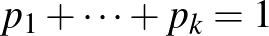 és
és 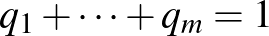
feltételek mellett kombinálja. Ha ellenfele a 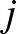 -edik stratégiáját játssza, az 1. játékos az
-edik stratégiáját játssza, az 1. játékos az 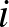 -ediket, és hasznossága
-ediket, és hasznossága 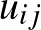 valós szám, akkor az 1. játékos várható hasznosságfüggvénye
valós szám, akkor az 1. játékos várható hasznosságfüggvénye
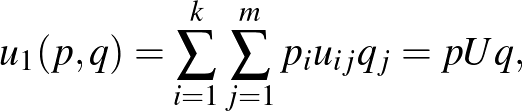 ahol
ahol 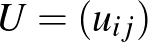
a nyeremények 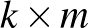 -es mátrixa. Ezeket a játékokat mátrixjátékoknak nevezzük.
-es mátrixa. Ezeket a játékokat mátrixjátékoknak nevezzük.
1. Tétel (Neumann (1928)). Minden kétszereplős nullaösszegű mátrixjátéknak létezik legalább egy egyensúlya.
A továbbiak miatt utalunk arra, hogy a létezés bizonyításához Neumann egy nevezetes tételt alkalmazott.
2. Tétel (Brouwer-féle fixponttétel, 1911). Legyen 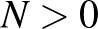 egy természetes szám. Tetszőleges folytonos
egy természetes szám. Tetszőleges folytonos 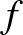 leképezésnek, amely az
leképezésnek, amely az 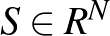 -beli korlátos és zárt konvex halmazt önmagára képezi le, létezik legalább egy
-beli korlátos és zárt konvex halmazt önmagára képezi le, létezik legalább egy 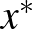 fixpontja:
fixpontja: 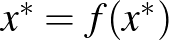 .
.
Neumann azt is belátta, hogy ha több egyensúly létezik, akkor azok csereszabatosak. Például jelölje a másik egyensúlypárt 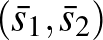 . Ekkor
. Ekkor 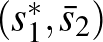 és
és 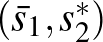 is egyensúly, valamint
is egyensúly, valamint 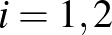 -re
-re
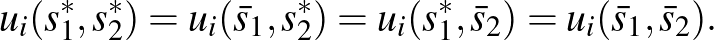
Morgenstern közreműködésével Neumann 1944-ben publikálta játékelméleti könyvét, amelyben azonban nehezen tudott elszakadni a kétszemélyes nullaösszegű játéktól, legalábbis a nemkooperatív részben. A könyvet számos kutató korszakalkotóként üdvözölte,3 a játékelmélet áttörésére azonban még meg kellett várni Nash egyensúlyelméletét. Érdekes, hogy Neumann, Morgenstern (1944) nem hivatkozik Cournot-ra!
A kétszemélyes nullaösszegű játékoknál megjelent dualitás később nagy hangsúlyt kapott Neumann 1938-ból származó gazdasági növekedési modelljében és Dantzig 1947-ben született lineáris programozásában (ez utóbbit Kantorovics 1939-ben publikálta először oroszul).
3. Nash felfedezése
Nash egy tehetséges matematikus diák volt Princetonban, ahol 21 éves korában, 1949-ben felfedezte az 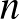 -személyes nemkooperatív játék általános egyensúlyi fogalmát. Legyen a játékosok száma
-személyes nemkooperatív játék általános egyensúlyi fogalmát. Legyen a játékosok száma 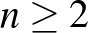 , indexük
, indexük 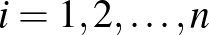 ; a stratégiahalmazok
; a stratégiahalmazok 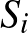 , a stratégiák
, a stratégiák 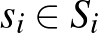 , a skalárértékű hasznosságfüggvények
, a skalárértékű hasznosságfüggvények 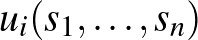 .
.
A továbblépés előtt célszerű lesz definiálni a kétszemélyes játékbeli domináns stratégiáját. Az 1. játékos 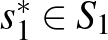 stratégiája domináns, ha bármely
stratégiája domináns, ha bármely 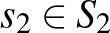 esetén legalább akkora hasznosságot nyújt az 1. játékosnak, mint bármely másik stratégiája. A 2. játékos
esetén legalább akkora hasznosságot nyújt az 1. játékosnak, mint bármely másik stratégiája. A 2. játékos 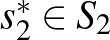 stratégiája is domináns, ha bármely
stratégiája is domináns, ha bármely 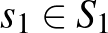 esetén legalább akkora hasznosságot nyújt a 2. játékosnak, mint bármely másik stratégiája. Együttesen az
esetén legalább akkora hasznosságot nyújt a 2. játékosnak, mint bármely másik stratégiája. Együttesen az 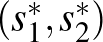 domináns egyensúly, amelytől egyoldalúan egyik játékosnak sem érdemes eltérnie:
domináns egyensúly, amelytől egyoldalúan egyik játékosnak sem érdemes eltérnie:
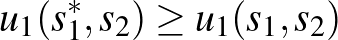 és
és 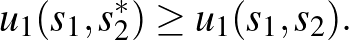
Talán a legnevesebb nem nullaösszegű kétszemélyes játék a közismert fogolydilemma (1950 körül, névadója, Tucker, Nash témavezetője volt), amelynek van domináns stratégiapárja. Mivel nem tudnak összebeszélni, mindkét fogoly jobban jár, ha elárulja a másikat, bármit tesz a másik. A legtöbb játékban azonban nincs domináns egyensúly (vö. a 2. és a 3. példát), ezért szélesebb érvényű definíciót kell keresni.
A folytatáshoz célszerű bevezetni egy Nash-től származó szellemes jelölést, amellyel az 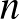 -személyes játék szinte 2-személyesre vezethető vissza: legyen
-személyes játék szinte 2-személyesre vezethető vissza: legyen
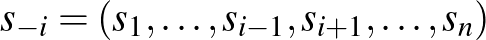
az 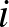 -edik játékos ellenfeleinek stratégiavektora, és
-edik játékos ellenfeleinek stratégiavektora, és 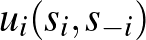 a megfelelő hasznosság.
a megfelelő hasznosság.
Nash egyensúlyi definíciója a következő: minden 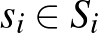 -re
-re
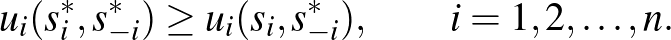
Szóban: semelyik játékosnak nem érdemes egyedül eltérnie az egyensúlytól.
Bemutatunk egy kétszemélyes, nem nulla összegű játékot, amelyben nem létezik domináns stratégiapár, de két Nash-egyensúly is létezik, amelyek azonban nem csereszabatosak.
2. példa. A nemek harca. A Fiú és a Lány szeret együtt lenni, de a Fiú inkább meccsre menne, a Lány inkább moziba. A kifizetési mátrixpár most legyen a következő:
| Lány Fiú |
mérkőzés | mozi |
| mérkőzés | 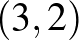 |
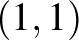 |
| mozi | 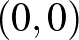 |
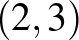 |
Valóban, a Fiú számára a „meccs” stratégia jobb, mint a „mozi”, ha a lány is meccsre megy (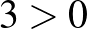 ), és a Lánynak is jobb, mint ha moziba menne (
), és a Lánynak is jobb, mint ha moziba menne (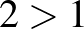 ). Hasonló érveléssel belátható, hogy a (mozi, mozi) pár is Nash-egyensúly. Felvetődik a kérdés: a résztvevők melyiket válasszák a két egyensúly közül? Hogyan koordinálja a szerelmespár a választást? (Hogy ne a lány menjen a meccsre és a fiú a moziba!)
). Hasonló érveléssel belátható, hogy a (mozi, mozi) pár is Nash-egyensúly. Felvetődik a kérdés: a résztvevők melyiket válasszák a két egyensúly közül? Hogyan koordinálja a szerelmespár a választást? (Hogy ne a lány menjen a meccsre és a fiú a moziba!)
Nash nemcsak definiálta az 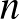 -személyes egyensúlyt, hanem létezését általános mátrixjátékokra bizonyította.
-személyes egyensúlyt, hanem létezését általános mátrixjátékokra bizonyította.
3. Tétel (Nash, 1951). Véges számú játékos véges mátrixjátékának mindig létezik legalább egy egyensúlya.
Érdekes, hogy Nash-nek nem jutott eszébe, hogy elszakadjon a mátrixjátékoktól, és olyan keretet alkosson, amelybe például a korábban említett Cournot-modell is belefér. Ezt a viszonylag könnyű feladatot követői végezték el. Megfelelő módon általánosítva a stratégiahalmazokat és a hasznosságfüggvényeket, maximálisan kiterjesztették az alaptételt. A következő definíciókra lesz szükségünk:
Definíciók. 1. Halmazértékű leképezésnek nevezünk két absztrakt halmaz, 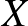 és
és 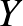 közötti
közötti 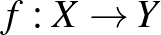 hozzárendelést, amely minden
hozzárendelést, amely minden 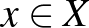 ponthoz egy
ponthoz egy 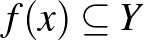 halmazt rendel. (Ha
halmazt rendel. (Ha 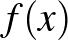 minden esetben pont, akkor függvényről beszélhetünk.)
minden esetben pont, akkor függvényről beszélhetünk.)
2. A folytonos függvény egyik lehetséges általánosításaként egy leképezést felülről félig folytonosnak nevezünk, ha bármely olyan 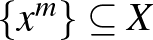 sorozatra, amely konvergál
sorozatra, amely konvergál 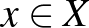 -hez, és bármely
-hez, és bármely 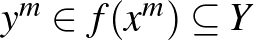 ,
, 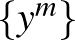 konvergál
konvergál 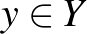 -hoz, akkor
-hoz, akkor 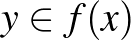 teljesül. Kompakt
teljesül. Kompakt 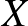 tér esetén ez azt jelenti, hogy az
tér esetén ez azt jelenti, hogy az ![$[x,f(x)]$](/images/stories/latexuj/2021-03/2021-03-simonovitsanashrejtely/img91.png) gráf zárt halmaz.
gráf zárt halmaz.
3. Egy 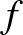 leképezésnek az
leképezésnek az 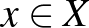 pont fixpontja, ha
pont fixpontja, ha 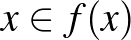 .
.
4. Az 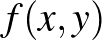 függvény kvázikonkáv, ha minden szintvonala konvex, azaz minden
függvény kvázikonkáv, ha minden szintvonala konvex, azaz minden 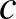 -re az
-re az 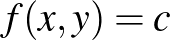 egyenletet kielégítő
egyenletet kielégítő 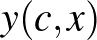 görbe konvex.
görbe konvex.
4. Tétel (Nikaido, Isoda (1955)). Egy 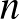 -személyes játéknak létezik legalább egy Nash-egyensúlya, ha teljesülnek a következő feltételek:
-személyes játéknak létezik legalább egy Nash-egyensúlya, ha teljesülnek a következő feltételek:
a) az 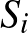 stratégiahalmaz egy
stratégiahalmaz egy 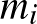 -dimenziós euklideszi tér nemüres, konvex és kompakt halmaza;
-dimenziós euklideszi tér nemüres, konvex és kompakt halmaza;
b) Az 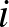 -edik játékos
-edik játékos 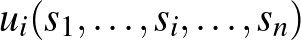 hasznosságfüggvénye folytonos minden változójában és kvázikonkáv
hasznosságfüggvénye folytonos minden változójában és kvázikonkáv 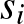 -ben,
-ben, 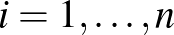 .
.
Érdekes módon a legkézenfekvőbb bizonyítási eszköz a Cournot-féle reakciófüggvényen alapul, amelyet a játékelméletben legjobb válasznak neveznek, és nem pont-, hanem halmazértékű: 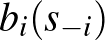 az
az 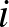 -edik játékosnak olyan stratégiai részhalmaza, hogy bármely elemét válasszuk is, nincs nála jobb válasz
-edik játékosnak olyan stratégiai részhalmaza, hogy bármely elemét válasszuk is, nincs nála jobb válasz 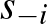 -re:
-re:
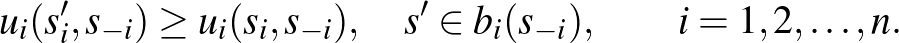
Ekkor a Nash-egyensúly tömörebben is megfogalmazható:

Megismételjük, Nash egy fixpontként adódó 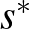 stratégiavektor létezését igazolta. A technikai bonyodalmakat elkerülendő, csak utalunk a bizonyítás alapötletére. Legyen
stratégiavektor létezését igazolta. A technikai bonyodalmakat elkerülendő, csak utalunk a bizonyítás alapötletére. Legyen 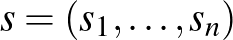 a stratégiák vektora, és legyen
a stratégiák vektora, és legyen
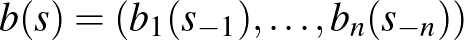
a legjobb válaszfüggvények vektora, s ennek 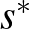 fixpontja:
fixpontja:
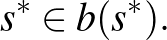
A fixpont létezésének a bizonyítása már csak matematikai technika kérdése.
5. Tétel (Kakutani fixpont-tétele, 1941). Ha 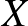 egy véges-dimenziós euklideszi tér nemüres, konvex és kompakt halmaza; ha
egy véges-dimenziós euklideszi tér nemüres, konvex és kompakt halmaza; ha 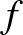 az
az 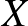 -nek egy önmagára való, felülről félig folytonos leképezése, amely minden
-nek egy önmagára való, felülről félig folytonos leképezése, amely minden 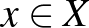 -hez nemüres konvex halmazt rendel, akkor
-hez nemüres konvex halmazt rendel, akkor 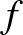 -nek létezik fixpontja:
-nek létezik fixpontja: 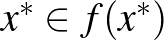 .
.
Nash (1951) sem hivatkozik Cournot-ra,4 de még Neumann (1928)-ra sem, csak Neumann, Morgenstern (1944)-re! Őt is túlzottan érdekelték a társasjátékok, ez magyarázza a szimmetrikus játékok külön tárgyalását és a póker modellezését. A következő példában azonban egy valódi közgazdasági modellben, egy 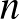 vállalatból álló oligopólium egyensúlyát mutatjuk be.
vállalatból álló oligopólium egyensúlyát mutatjuk be.
3. példa. Tegyük föl, hogy 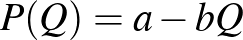 a piaci ár–keresleti függvény, és mindegyik vállalat költségfüggvénye
a piaci ár–keresleti függvény, és mindegyik vállalat költségfüggvénye 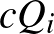 , ahol
, ahol 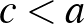 . Az
. Az 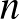 -szereplős oligopolista egyensúlyban mindegyik vállalat egyensúlyi kibocsátása azonos, és fordítva arányos
-szereplős oligopolista egyensúlyban mindegyik vállalat egyensúlyi kibocsátása azonos, és fordítva arányos 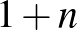 -nel:
-nel:
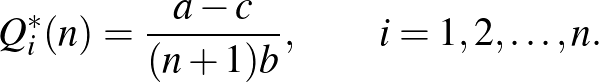
Hangsúlyozzuk, hogy minél több egyforma vállalat verseng egymással, annál nagyobb az össztermelés:
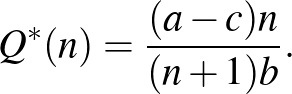
és annál alacsonyabb a piaci ár:
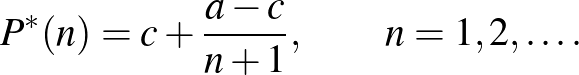
Határértékben megvalósul a tökéletes verseny:
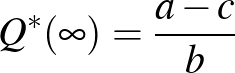 és
és 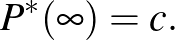
Szomorú, hogy amikor Nash személyesen közölte Neumann-nal korszakalkotó eredményét, Neumann képtelen volt felkarolni az eredményt: „Fixponttétel” – utalt a bizonyítás számára nyilvánvaló alapjára, és másra terelte a beszélgetést. (Az említett interjúban Nash nem szomorkodik, és még egy tévedést elkövet: „a játékelméletben ő [Neumann] nem használt fixpont-tételeket.” Dehogynem. Más kérdés, hogy a konvex halmazokat elválasztó síkjának létezését kimondó tétel is elegendő lett volna a mátrixjátékok minmax-tételének bizonyításához.)
Bár a Kuhn–Tucker cikkben (Kuhn, Tucker (1958)), amely Neumann játékelméleti és közgazdaságtani eredményeit tekinti át, már megjelenik Nash (1951), de eléggé haloványan. Ugyanakkor az általános egyensúlyelmélet klasszikus kifejtésében a létezési tétel bizonyítása (Arrow, Debreu (1954)) már a Nash-egyensúlyra épült.5
Zárásként megemlítjük, hogy 1950/51-es megjelenése óta a Nash-egyensúly a nemkooperatív játékelmélet alapja lett. Ez nem jelenti azonban azt, hogy a Nash-egyensúly minden nemkooperatív játékelméleti kérdést megold. Az elméletnek csupán két problémáját említem meg, azokat is csak távirati stílusban:
– Ha több egyensúly létezik (nemek harca), akkor hogyan koordinálják a játékosok a választásukat (Selten, 1965)?
– Mi történik, ha a játékosok nem ismerik egymás stratégiahalmazait és hasznosságfüggvényeit (Harsányi, 1967)?
A Nash-egyensúly beérését jól jelzi, hogy 1994-ben először kaptak játékelméleti kutatók közgazdasági Nobel-díjat. Nash mellett a másik két díjazott az imént említett Harsányi és Selten volt. Ha az 1903-ban született Neumann megéri a díj 1969-es alapítását, akkor nagy valószínűséggel az első díjazottak közt lett volna – akár a növekedési modelljéért, akár a Neumann–Morgenstern-féle hasznosságfüggvény megalkotásáért.
Irodalomjegyzék
- K. Arrow, G. Debreu (1954) „Existence of Equilibrium for a Competitive Economy”, Econometrica 22, 265–290. o.
J. Bertrand (1883) „Theorie mathematique de la richesse sociale et recherches sur les principles mathematiques de la theorie des richesses”, Journal de Savants 67, 499–508. o.
A. Cournot (1838) Researches into the Mathematical Principles of the Theory of Wealth francia eredeti angol fordítása, 1897.
W. Fellner (1949) Competition among the Few. New York, Knopf.
H. Hotelling (1929) „Stability of Competition”, Economic Journal 39 41–57. o.
L. Hurwicz (1945) „The Theory of Economic Behavior,” American Economic Review, 35, 909–925. o.
H. Kuhn, A. W. Tucker (1958) „John von Neumann's Work on the Theory of Games and Mathematical Economics”, Bulletin of American Mathematical Society, 1958.
R. J. Leonard (1994) „Reading Cournot, Reading Nash: The Creation and Stabilization of the Nash Equilibrium,” The Economic Journal, 104, 492–511. o.
J. Marschak (1946) „Von Neumann and Morgenstern's New Approach to Statc Economics”, Journal of Political Economy 54, 97–115. o.
S. Nasar (1998) Egy csodálatos elme, az angol eredeti magyar fordítása, Bp. Gabo, 2002.
J. Nash (1950a) „Equilibrium Points in 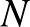 -Person Games”, Proceeding of the National Academy of Scieneces of the USA, 36:1, 48–49. o.
-Person Games”, Proceeding of the National Academy of Scieneces of the USA, 36:1, 48–49. o.
J. Nash (1950b) „The Bargaining Problem”, Econometrica, 18, 155-162. o.
J. Nash (1951) „Non-Cooperative Games”, Annals of Mathematics, 2nd series, 54:2, 286–295. o.
J. Neumann (1928) „Zur Theories der Gesellschaftsspiele”, Math. Ann. 100, 295–320.
J. Neumann, O. Morgenstern (1944) Theory of Games and Economic Behavior, Princeton Univ. Press, Princeton NJ, első kiadás.
J. Neumann (1965) Válogatott előadások és tanulmányok, Budapest, KJK, 1965.
H. Nikaido, K. Isoda (1955) „Note on Noncooperative Convex Games”, Pacific Journal of Mathematics 5, 807–815. o.
M. Raussen, C. Skau (2015) Interjú Nash-sel, fordította Matolcsi Máté, Érintő, 2016, szept. https://ematlap.hu/interjuk-portrek-2016-09/326-interju-a-2015-ben-abel-dijat-nyert-john-f-nash-jr-professzorral
J. Schumpeter (1954) 19 [19] History of Economic Analysis. NYC, Oxford University Press.
H. von Stackelberg (1934) The Theory of the Market Economy, London, W. Hodge, a német eredeti angol fordítása.
Simonovits András
ELKH KRTK KTI, BME, MI
Lábjegyzetek
- 1 Köszönettel tartozom Madarász Aladárnak, aki fölhívta a figyelmem Leonard (1994) cikkére, amelynek néhány megállapítására lábjegyzetekben hivatkozom. A részletek után érdeklődőknek ajánlom a teljes cikk elolvasását.
- 2 Két további fontos Cournot-hivatkozást idézek Leonard (1994)-ből: Stackelberg (1934) dinamikusan kiterjesztette a Cournot-egyensúlyt vezető és követő vállalatra, Fellner (1949) elutasította Cournot reakciógörbéin alapuló rejtett dinamikát.
- 3 Azonnali recenziók Neumann, Morgenstern (1944)-ről: Hurwicz (1945) és Marschak (1946).
- 4 Az alkuról szóló Nash (1950b) cikk viszont megemlíti Cournot nevét is.
- 5 Figyelemre méltó, hogy a princetoni és más közgazdászok először hevesen ellenezték a játékelmélet közgazdasági térfoglalását.









