Varga Tamás igazi vérbeli pedagógus családjában, ősei és rokonai között sok kiváló matematikus és pedagógus volt. Így már a „génjeiben” benne lehetett, hogy a matematikát nem csak művelni kell, de legalább olyan fontos jól megtanítani. Igazából nem is annyira a népes és jól ismert családfáról szeretnék írni, (a családfát tanulmányozóknak szíves figyelmébe ajánljuk a kitűnő honlapot: http://csalad.szemerja-szasz.hu) sokkal inkább a családfa 18. századi megteremtőjéről, a matematikus, jogász, államférfi, nyelvész, irodalmár id. szemerjai Szász Károlyról.
Szabó János festménye: Szász Károly (Vízakna, 1798. január 25. - Marosvásárhely, 1853. október 25.) államférfi, jogtudós, író, matematikus. Forrás: https://commons.wikimedia.org/wiki/File:Sz%C3%A1sz_K%C3%A1roly_(Szab%C3%B3_J%C3%A1nos_festm%C3%A9nye).jpg
.jpg){kind=link}
A szemerjai Szász-család jól ismert a magyar művelődéstörténetben, elég, ha csak Arany János barátjára, a nagy irodalmár Szász Károly (Nagyenyed, 1829. június 15. – Budapest, 1905. október 15.) püspökre gondolunk, (négy „nagy” Szász Károlyt ismer a magyar művelődéstörténet), de ebből a családból származik, a néhai Szász Domokos (Nagyenyed, 1838. május 25. – Kolozsvár, 1899. január 8.) irodalmár, egyetemi tanár, erdélyi református püspök, Szilágyi Domokos (Nagysomkút, 1938. július 2. – Kolozsvár, 1976. november 2.) kiváló erdélyi költő, Varga Domokos (Kunszentmiklós, 1922. október 8. – Budapest, 2002. május 12.) irodalomtörténész, Dr. Szász Pál (Budapest, 1901. július 11. – Budapest, 1978. február 12.) matematika professzor, Dr. Szász Domokos matematikus, az MTA volt alelnöke és természetesen Varga Tamás, hogy csak a legismertebb személyiségeket említsük.
A matematikus, pedagógus id. Szász Károly mindkét Bolyainak közeli barátja volt. Kevesen tudják, hogy a szakoktatás bevezetése 1848-as vívmány, mert addig az oktatásban is feudális állapotok uralkodtak. A 48-as első független, felelős magyar kormányban a kultuszminiszter báró Eötvös József volt és id. Szász Károly volt az államtitkára. Már báró Eötvös József kiadta a szakoktatás bevezetésének rendeletét (vagyis, hogy szaktantárgyat csak szakember taníthat), de akkora ellenállásba ütközött, hogy lemondott és utána id. Szász Károly vezette a kultuszminisztériumot 1848. szeptember 28-tól 1849. május 1-ig.
Szász Károly képe a Wikipédián.
Ő kiváló matematikatár volt Nagyenyeden, majd az 1848-as forradalom bukása után Marosvásárhelyen. Szinte minden diákja rajongott érte, és kiváló hallgatói (báró Kemény Zsigmond író, Koós Ferenc református lelkipásztor, Mentovich Ferenc filozófus, természettan tanár) emlékirataikban megírták, hogy id. Szász Károly óráin értették meg a matematikát. Például Koós Ferenc írta, hogy Bolyai Farkas matematikai óráin semmit sem értettek, de szerencsére Bolyai Farkas nyugdíjaztatása után, id. Szász Károly óráin minden érthető lett, és megvilágosodott előttük a matematikai fogalmak értelme.
Id. Szász Károly és fia, a későbbi református püspök Szász Károly írtak egy „Számtan” könyvet, mely Pesten jelent meg 1853-ban[1]. Könyvükben összefoglalják a közoktatásban használatos matematikai ismereteket. Kezdeményezik a logaritmus fogalmának bevezetését a közoktatásba, és erre egy nagyon szemléletes jelölést is javasolnak:
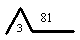olvasd: „nyolczvanegynek három alapu logarithma” vagy is: „az a’ szám hányadik emelete nyolczvanegy háromnak.
§. 24. Gyökér.
A’ gyökér’ jelentésének (ezen két fél ’s egy egész szó’ kifejezésének: -nak, -dik gyökere) ismét nem csak egy hanem két alakja divatoz az Algebrában.
Leírjuk az emeletet, (a’ számot melynek gyökeréről szólunk), egy ily alaku jegyet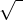 
(maradványát a’ gyökér’ latin neve’ – radix – kezdő betűjének) rajzolunk elébe az emelet fölött elnyúló szárral, ’s ennek öblébe helyezzük a’ logarithmot (azt a’ számot, hányadik gyökerét akarjuk jelelni a’ fönforgó emeletnek). Pl. ; 
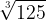olvasd: „százhuszonötnek harmadik gyökere”; más szókkal: „az a’ szám melynek harmadik emelete százhuszonöt;” latinosan: „radix három (v. tertia) ex százhuszonöt.” Itt is két pótjegyzetünk van.
a, Valamint minden szám maga magának első emelete, úgy, és éppen azért, első gyökere is. Akármely szám első gyökere helyett tehát mindig bártan oda írhatjuk, ’s szoktuk is írni, egyenesen magát azt a’ számot; pl.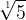 
helyett csak ezt: 5;, , sat. 
, 
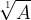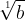helyett ezeket: A, b sat. Ha pedig, akármi okból, csakugyan ily esetben is használni akarnók a’ gyökérjegyet, az 1 belőle soha el nem maradhat; mert:
b, Olyan gyökérjegy’ ölébe, melyhez semmi szám írva nincs, egyezményileg mindig 2 értetik. Oka pedig ezen egyezménynek nem egyéb mint az, hogy minden gyökerek köztt a’ második gyökér fordul leggyakrabban elé, ’s azért leg több írást úgy kimélünk ha ennek kihagyására szabaditjuk föl magunkat, az üres öbölbe 2-t értvén mindenkor. E’ szerint tehát annyi mint 
’s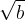 
, , , , sat. nem egyebek mint 
, 
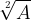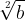, , , sat[2].
§. 25. Logarithm.
A’ logarithmnak mint eredménynek, az emelet és gyökér mint ereditők általi, közvetőleges kifejezésére saját alakot, köz egyezéssel, még nem fogadtak-el a’ számtanárok; azonban erre is múlhatlan szükség levén, mí teszünk egy javaslatot, ’s azt ezen könyvünk’ folytában tettleg alkalmazzuk is; miszerint, logarithm’ jelelésül használhassék a’ gyökérjegy, hegyével fől ’s nyilával lefelé forditva, ily formán: 
Ennek ölébe írassék a’ gyökér, után az emelet, ’s a’ két szám a’ jegygyel egyesülten jelentse a’ logarithmot, t.i. azt a’ számot, hányadik emelete az utolsó az elsőnek.
A „Számtan” könyv 30-31.oldala
Id. és ifj. Szász Károly bevezetett egy pár műszót a matematikai szakirodalomba. Jó nyelvészek és nagy irodalmárok is lévén, ez érezhető műszavaikban, de könyvükben is. Érthetően és olvasmányosan írták meg matematikai tankönyvüket. E sorok írójának az a véleménye, hogy az 1853-ban Pesten kiadott „Számtan”-könyvük lényegében id. Szász Károly Nagyenyeden tartott leckéit tartalmazza, a fia tolmácsolásában. Nagyenyeden Szász Károly, miután kitúrták a jogi katedráról, matematikát tanított és így tanította fiát, és az ugyancsak kiváló matematikust és irodalomtudóst, Mentovich Ferencet.
Szász Károly alkotta szavak például:
hatványozni (17. old.)
semmítőleges szám = negatív szám (157, 180 old.)
tényleges szám = pozitív szám
aequalitas = egyenlőség (44 old.)
algebra = elméleti számtan (10. old.)
denominator = alsó (179 old.)
irrationalis = határozatlan jegyű (197 old.)
logarithma = logarithmozás (197. old)
Most lássunk még egy részletet Szász Károly Számtankönyvéből: §. 33 Vagy – vagy. Mind – mind. Kérdés. Átviteli jelelés.
Hátra vagynak még némely ritkábban használt, de mégis hallgatással nem mellőzhető, jelelések, melyeknek magyarázatával tehát nyelvtanunkat ez úttal bérekesztjük.
Mint köz beszédeben, úgy Algebrában is, mondatunk néha több águ, és pedig több águ lehet vagy választólag vagy egybefoglalólag.
Valasztólag több águ, ha valamely számról emlitett két, három, ’s több mondotak közől vagy egyiket, vagy másikot, ’s tehát valamelyiket, de korán sem mindeniket akarjuk érteni. Pl. Ha ezen sorozatból 1-1+1-1+… akárhány egymást követő tagot vesszük, öszves értékök vagy 1 lesz vagy 0;
1, ha a’ vett tagok’ száma páratlan;
0, ha páros;
Egy ily választó mondat’ leírási módszere, azoknak, mikről válaszlólag szólunk, egymás’ fölibe helyezéséből áll. Tehát a’ fölhozott első példát így írjuk:
Eddig az idézet. Maga a példa nagyon fontos! Tudniillik az 1 -1 +1 -1 +1 -1 +1 -1+… végtelen sor összegzéséről van szó, amelynek külön matematikatörténeti múltja van. Ennek a sornak az összege sok fejtörést okozott Bolyai Farkasnak, a kiváló matematikus és csillagász Nagy Károlynak, az Egyetemes számtudomány szerzőjének, Vállas Antalnak és Szász Károlynak, és az tette híresé, hogy Euler is megvizsgálta a fenti alternáló sort és konvergensnek találta, vagyis kimondta róla, hogy van összege és az egyenlő ½-del. Nos, ma minden elsőéves műszakis (matematikus stb.) hallgató kell, hogy tudja, hogy a fenti sor divergens. Tehát, bármennyire is meglepő, de a nagy Euler itt tévedett. Mondhatnánk, hogy ha Euler hibázott, akkor a 200 arannyal jutalmazott Nagy Károlynak is meg lehet ezért bocsátani. Viszont Euler száz évvel Nagy Károly előtt élt, és száz év alatt sokat fejlődött matematika, főleg annak fogalmi rendszere. A legnagyobb gondot Euler idejében az okozta, hogy nem volt még a sor és sorozat pontos fogalmi rendszere tisztázva. Ezért pontatlan meghatározással indulva, könnyen lehetett tévútra menni.
2017. szeptember 13–15. között Balatonfüreden egy igen eredeti Pólya-emlékkonferenciát tartottak „Te hogyan oldottad meg?” – A matematikai felfedezés iskolája és története címmel.
Pósa Lajos nagyon érdekes oktatóvideót mutatott be a +1, +1-1, +1-1+1, +1-1+1-1, +1-1+1-1+1… alternáló sorozatról. Abban az oktatóvideóban adtak egy nagyon „jópofa” transzcendens értelmezést is. Kár, hogy a videóban nem szerepel ennek az alternáló végtelen sornak a magyar matematikatörténeti háttere.
Szász Károly a felsőbb matematikában is járatos volt. Ő is felfedezte a végtelen sor egy konvergencia kritériumát:
Tétel (id. Szász Károly)[3].
Ha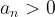 
szigorúan növekvő, akkor 
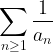akkor és csakis akkor konvergens, ha
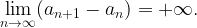
Végezetül az érdeklődő olvasók figyelmébe ajánljuk id. Szász Károlyról írt könyvünket, melyet Farkas Péter balatonboglári irodalomtörténésszel, id. Szász Károly dédunokájával és Varga Tamás másod-unokatestvérével közösen írtunk: Farkas Péter, Oláh-Gál Róbert: A leghíresebb helyettes tanár Szász Károly, Pro-Print Könyvkiadó, Csíkszereda, 2019.
Ennek a könyvnek az előzménye, amelyben id. Szász Károly fiáról, Szász Károly püspökről és Arany János jó barátjáról tudhatnak meg érdekes, eddig ismeretlen részleteket az olvasók: Oláh-Gál Róbert: Arany János és erdélyi barátai, Pro-Print Könyvkiadó, Csíkszereda, 2019.
Oláh-Gál Róbert,
a Sapientia Erdélyi Magyar Tudományegyetem Csíkszeredai Karának adjunktusa
Irodalomjegyzék
[1] Számtan. Új elvek szerint. Elméleti számtan (Algebra). Dolgozták idősb Szász Károly, Magyar Tudós Társaság rendes tag, volt enyedi tanár és ifj. Szász Károly nagy-kőrösi tanár, Pest, Heckenast Gusztáv sajátja. 1853. VIII. 215 p.
[2] 114, 115 old. Számtan
[3] Lásd részletesebben: Sándor József, Oláh-Gál Róbert: Bolyai Farkas sorelméleti vizsgálatairól és a hozzá kapcsolódó fejleményekről, 2010., 2., Matematikai Lapok., HU ISSN 0025-519X., pp. 18-37.