Tekintsük a következő (nem igazán életszerű) problémát: adott egy gödrünk, és azt kérdezzük, hogy készíthető-e hozzá egy olyan négyzet keresztmetszetű cövek, amely épp befér a gödrünkbe, vagyis alapjának csúcsai épp a gödör szélén vannak. Mi a helyzet, ha téglalap keresztmetszetű cövekekkel szeretnénk dolgozni?
A fenti (a gyakorlati életben azért, valljuk be, ritkán előforduló) probléma vezethette Otto Toeplitz neves német matematikust a következő, nagyon egyszerűen megfogalmazható, de meglepően mély eszközöket kívánó probléma felvetéséhez. Legyen 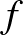 egy, az
egy, az  körvonalról az
körvonalról az 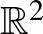 síkba mutató folytonos, injektív függvény, vagyis az
síkba mutató folytonos, injektív függvény, vagyis az 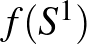 kép egy egyszerű (önátmetszések nélküli) folytonos zárt görbe
kép egy egyszerű (önátmetszések nélküli) folytonos zárt görbe 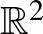 -ben. Az ilyen
-ben. Az ilyen 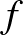 függvényt (injektivitása okán) néha beágyazásnak is hívjuk, a képként előálló
függvényt (injektivitása okán) néha beágyazásnak is hívjuk, a képként előálló 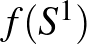 görbét pedig Jordan-görbének is szokás nevezni. (Ez a görbe jelképezné a kiásott gödrünk peremét kertünkben, amelyet síknak képzelünk.)
görbét pedig Jordan-görbének is szokás nevezni. (Ez a görbe jelképezné a kiásott gödrünk peremét kertünkben, amelyet síknak képzelünk.)
Négyzetes cövek sejtés (Topelitz [10], 1911): Minden fenti 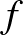 esetén létezik négy különböző olyan
esetén létezik négy különböző olyan 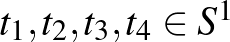 pont, hogy
pont, hogy 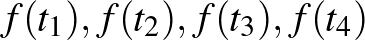 képük egy négyzet négy csúcsát határozzák meg, lásd az alábbi ábrát.
képük egy négyzet négy csúcsát határozzák meg, lásd az alábbi ábrát.
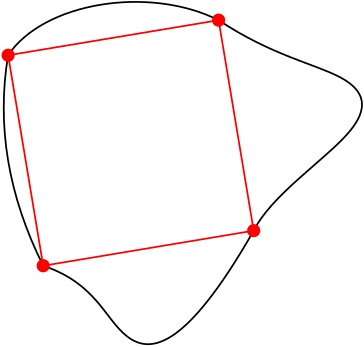
Az 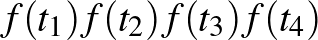 négyzetet (a fogalmat kicsit tágítva) a továbbiakban beírt négyzetnek is fogjuk hívni, bár nemkonvex
négyzetet (a fogalmat kicsit tágítva) a továbbiakban beírt négyzetnek is fogjuk hívni, bár nemkonvex 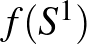 Jordan-görbe esetén ez a négyzet nem lesz feltétlen része a görbe által határolt körlapnak – de legalább csúcsai a görbén vannak. (A gödrökkel megfogalmazott analógiában általában konvex görbékre gondolunk; a cövek nem feltétlenül fér be a gödörbe a nemkonvex esetben.) A fenti matematikai problémában az
Jordan-görbe esetén ez a négyzet nem lesz feltétlen része a görbe által határolt körlapnak – de legalább csúcsai a görbén vannak. (A gödrökkel megfogalmazott analógiában általában konvex görbékre gondolunk; a cövek nem feltétlenül fér be a gödörbe a nemkonvex esetben.) A fenti matematikai problémában az 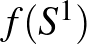 -ről konvexitást nem tételezünk fel.
-ről konvexitást nem tételezünk fel.
A matematikai feladat gyengíthető úgy, hogy a négy képponttól azt követeljük meg, hogy egy (nemelfajuló, tehát nem szakasznak kinéző) téglalap négy csúcsát alkossák.

A feladat nehezíthető is: megkérdezhetjük, hogy rögzített görbére és tetszőlegesen rögzített téglalapra van-e négy olyan pont, amely a rögzített téglalapunkhoz hasonló téglalap négy csúcsát alkotja. Emlékezzünk, hogy két téglalap pontosan akkor hasonló, ha az oldalhosszaik aránya (amiről az oldalak felcserelése árán feltehető, hogy legalább 1) egyenlőek. A négyzet esetét kapjuk akkor, amikor ez az arányszám 1-gyel egyenlő. A sejtés utóbbi két változatát téglalapos cövek problémának szokás hívni.

Az alábbiakban ezen problémák rövid története és a megoldásukban a közelmúltban történt áttörések kerülnek bemutatásra. (A probléma jóval részletesebb tárgyalását Benjamin Matschke kitűnő cikkében [5] lehet megtalálni.)
1. A négyzetes cövek probléma
A probléma megoldását már 1913-ban megtalálta Arnold Emch [2] abban az esetben, ha az 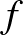 függvény szakaszonként analitikus. A simasági feltételt gyengítette Schnirelman [8] egy 1929-ben írt dolgozatában (melynek javított változata 1944-ben jelent meg). Mindkét bizonyítás alapötlete megtalálható Matschke fent említett [5] cikkében. Első pillantásra az ember azt gondolhatná, hogy a sima (differenciálható) eset kezelésével a probléma megoldódik: egy tetszőleges
függvény szakaszonként analitikus. A simasági feltételt gyengítette Schnirelman [8] egy 1929-ben írt dolgozatában (melynek javított változata 1944-ben jelent meg). Mindkét bizonyítás alapötlete megtalálható Matschke fent említett [5] cikkében. Első pillantásra az ember azt gondolhatná, hogy a sima (differenciálható) eset kezelésével a probléma megoldódik: egy tetszőleges 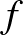 beágyazást közelítsünk
beágyazást közelítsünk 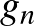 sima beágyazások egy sorozatával, melyekre már tudjuk, hogy léteznek a megkívánt beírt négyzetek. Vegyük ilyen négyzetek egy sorozatát, és érveljünk úgy, hogy ennek a négyzetsorozatnak van konvergens részsorozata. Valójában ez az érvelés percízzé tehető; az egyetlen probléma az, hogy a kapott négyzetsorozat könnyen elképezelhetően egy degenerált (0 oldalhosszúságú) négyzethez fog konvergálni (amikor is a sejtésben megkívánt
sima beágyazások egy sorozatával, melyekre már tudjuk, hogy léteznek a megkívánt beírt négyzetek. Vegyük ilyen négyzetek egy sorozatát, és érveljünk úgy, hogy ennek a négyzetsorozatnak van konvergens részsorozata. Valójában ez az érvelés percízzé tehető; az egyetlen probléma az, hogy a kapott négyzetsorozat könnyen elképezelhetően egy degenerált (0 oldalhosszúságú) négyzethez fog konvergálni (amikor is a sejtésben megkívánt 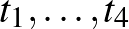 pontok egybeesnek). Mivel ezt a sejtés kizárja, így a fenti gondolatmenet nem visz közelebb a megoldáshoz.
pontok egybeesnek). Mivel ezt a sejtés kizárja, így a fenti gondolatmenet nem visz közelebb a megoldáshoz.
Mint kiderült, a probléma nehézsége valóban az 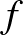 beágyazás analitikus tulajdonságaiban rejlik. Napjaink egyik kiemelkedő matematikusa, Terence Tao is egy hosszú cikket szentelt a problémának [9] abban az esetben, ha az
beágyazás analitikus tulajdonságaiban rejlik. Napjaink egyik kiemelkedő matematikusa, Terence Tao is egy hosszú cikket szentelt a problémának [9] abban az esetben, ha az 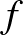 képeként előálló görbe két (további tulajdonságoknak is eleget tevő) Lipschitz-függvény grafikonjából rakható össze. Az általános, folytonos
képeként előálló görbe két (további tulajdonságoknak is eleget tevő) Lipschitz-függvény grafikonjából rakható össze. Az általános, folytonos 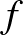 -re vonatkozó négyzetes cövek sejtés még ma is nyitott.
-re vonatkozó négyzetes cövek sejtés még ma is nyitott.
2. A téglalapos cövek probléma
Látványosabb volt a fejődés a téglalapos cövek probléma terén. Az egyszerűbb kérdésre, hogy vajon mindig létezik-e egy beírt téglalap, Vaughan már a 70-es években megtalálta a megoldást (ez Meyerson [6] cikkében jelent meg). Érdekes módon, a bizonyítás topológiai alapgondolatokon nyugszik. (A megoldás egy animált változata megtekinthető a youtube-on.)
Téglapos cövek tétel: Legyen 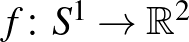 egy folytonos beágyazás. Ekkor létezik négy különböző olyan
egy folytonos beágyazás. Ekkor létezik négy különböző olyan 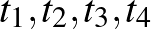 pont, hogy képük egy téglalap négy csúcsát adja.
pont, hogy képük egy téglalap négy csúcsát adja.
Bizonyítás: Vegyük azt a körvonal pontpárjain értelmezett
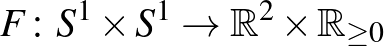
függvényt, mely a 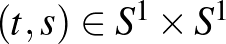 pontpárhoz az
pontpárhoz az
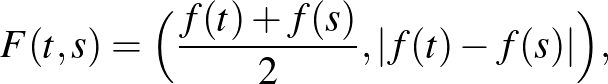
a háromdimenziós tér felső félterébe eső vektort rendeli. Könnyen látható, hogy  szimmetrikus a két változóban, így valójában az
szimmetrikus a két változóban, így valójában az 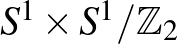 faktoron is értelmezhető (ahol a faktorizálással egybeejtjük a
faktoron is értelmezhető (ahol a faktorizálással egybeejtjük a  és
és 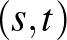 alakú párokat). Vegyük észre, hogy a
alakú párokat). Vegyük észre, hogy a 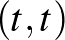 alakú elemeknek nincs párja. Nem teljesen triviális, de nem is nehéz látni, hogy az
alakú elemeknek nincs párja. Nem teljesen triviális, de nem is nehéz látni, hogy az  faktor épp a nevezetes
faktor épp a nevezetes  Möbius-szalaggal lesz azonos, melynek körvonal pereme épp a
Möbius-szalaggal lesz azonos, melynek körvonal pereme épp a 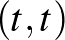 alakú elemekből áll. (Például, ha az
alakú elemekből áll. (Például, ha az 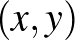 pontpárból azon az
pontpárból azon az 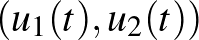 úton indulunk, amelynél
úton indulunk, amelynél 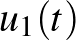 az
az  -ből
-ből 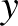 -ba mutató egyik köríven megy végig, míg
-ba mutató egyik köríven megy végig, míg 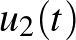 az
az 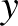 -ből
-ből  -be mutató másikon, így érve
-be mutató másikon, így érve 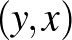 -be, akkor az
-be, akkor az 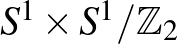 faktorban egy irányításfordító hurkon haladunk végig.)
faktorban egy irányításfordító hurkon haladunk végig.)
Ilymódon 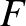 helyett nézhetjük az
helyett nézhetjük az 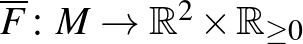 indukált leképezést. Vegyük észre, hogy pontosan akkor létezik az
indukált leképezést. Vegyük észre, hogy pontosan akkor létezik az  által adott görbe esetén beírt téglalap, ha
által adott görbe esetén beírt téglalap, ha  nem beágyazás: valóban, ha
nem beágyazás: valóban, ha  és
és 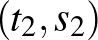 is ugyanoda képződik
is ugyanoda képződik 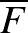 mentén, akkor az
mentén, akkor az 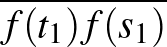 és
és 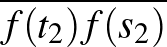 szakaszok egyforma hosszúak és közös a felezőpontjuk, tehát egy téglalap két átlóját adják.
szakaszok egyforma hosszúak és közös a felezőpontjuk, tehát egy téglalap két átlóját adják.
Tegyük fel indirekten tehát, hogy egy adott 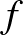 esetén nincs beírt téglalapunk. Ekkor
esetén nincs beírt téglalapunk. Ekkor 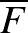 beágyazás, mely a Möbius-szalag peremét (a
beágyazás, mely a Möbius-szalag peremét (a 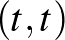 alakú párokat) viszi csak az
alakú párokat) viszi csak az 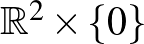 síkba, és ezeket a párokat épp az
síkba, és ezeket a párokat épp az 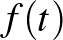 pontokba képezi. A topológia egy ismert tétele szerint az
pontokba képezi. A topológia egy ismert tétele szerint az 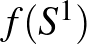 Jordan-görbe a síkot két részre bontja: egy körlapra, és egy nemkompakt részre. (Ezt a tételt Jordan görbetételeként ismerhetjük.) Ilymódon a beágyazott
Jordan-görbe a síkot két részre bontja: egy körlapra, és egy nemkompakt részre. (Ezt a tételt Jordan görbetételeként ismerhetjük.) Ilymódon a beágyazott  Möbius-szalaghoz hozzáragaszthatjuk a körlapot, amivel egy beágyazott projektív síkot kapunk a szokásos
Möbius-szalaghoz hozzáragaszthatjuk a körlapot, amivel egy beágyazott projektív síkot kapunk a szokásos 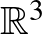 háromdimenziós terünkben. (Azt nem részletezzük, hogy miért igaz az, hogy a körlap és a Möbius-szalag összeragasztása az
háromdimenziós terünkben. (Azt nem részletezzük, hogy miért igaz az, hogy a körlap és a Möbius-szalag összeragasztása az 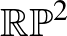 projektív síkot adja, de megjegyezzük, hogy ezt nem nehéz belátni.) Az algebrai topológia standard eszközeivel (például egész együtthatós homológiacsoportokkal, és az azokra vonatkozó Mayer-Vietoris hosszú egzakt sorozattal) azonban belátható, hogy
projektív síkot adja, de megjegyezzük, hogy ezt nem nehéz belátni.) Az algebrai topológia standard eszközeivel (például egész együtthatós homológiacsoportokkal, és az azokra vonatkozó Mayer-Vietoris hosszú egzakt sorozattal) azonban belátható, hogy 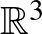 -ba nem lehet a projektív síkot beágyazni, vagyis hogy egy folytonos
-ba nem lehet a projektív síkot beágyazni, vagyis hogy egy folytonos 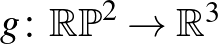 függvény soha nem lehet injektív. (Többszörös pontokkal rendelkező függvényt persze lehet találni, egy nevezetes ilyen leképezést ad a Boy-felület, melynek szobrászati megvalósítása az oberwolfachi konferenciaközpont előtt is megcsodálható.)
függvény soha nem lehet injektív. (Többszörös pontokkal rendelkező függvényt persze lehet találni, egy nevezetes ilyen leképezést ad a Boy-felület, melynek szobrászati megvalósítása az oberwolfachi konferenciaközpont előtt is megcsodálható.)

Forrás: https://commons.wikimedia.org/wiki/File:Boysche_Fl%C3%A4che_in_Oberwolfach.jpg
A talált ellentmondás szerint 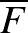 nem lehet injektív, így megvan a téglalapunk. Mivel a projektív sík folytonosan sem ágyazható be háromdimenziós terünkbe, a fenti gondolatmenetben
nem lehet injektív, így megvan a téglalapunk. Mivel a projektív sík folytonosan sem ágyazható be háromdimenziós terünkbe, a fenti gondolatmenetben 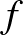 -ről csak folytonosságát kellett feltegyük.
-ről csak folytonosságát kellett feltegyük.
3. Újabb fejlemények
Vegyük észre, hogy a fenti bizonyítás semmifajta információt nem adott arra nézve, hogy a görbe milyen téglalapot tartalmaz (hasonlóság erejéig). A téglalapos cövek probléma erős változata szerint (hasonlóság erejéig) minden téglalapnak elő kellene fordulnia egy 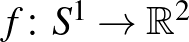 injektív függvény beírt téglalapjai között. Ebbe az irányba indult el Cole Hugelmeyer (első éves doktoranduszként) a következő eredményével:
injektív függvény beírt téglalapjai között. Ebbe az irányba indult el Cole Hugelmeyer (első éves doktoranduszként) a következő eredményével:
Tétel (Hugelmeyer, [4]) Ha 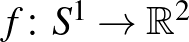 egy differenciálható beágyazás, akkor van olyan beírt téglalapunk, mely oldalainak aránya
egy differenciálható beágyazás, akkor van olyan beírt téglalapunk, mely oldalainak aránya  .
.
(Hugelmeyer eredménye ennél valamivel általánosabb, de ez a leglátványosabb, legegyszerűbben megfogalmazható eset, egyben bizonyítása tartalmazza az összes alapötletet.)
Hugelmeyer bizonyításának fő ötlete egyrészt az, hogy (az  azonosítást használva) a korábbi
azonosítást használva) a korábbi 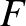 függvény egy
függvény egy 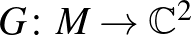 függvényre cserélhető, melyet a
függvényre cserélhető, melyet a
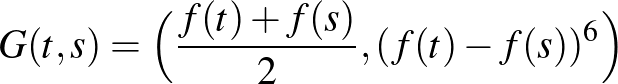
formula ad meg. Ismét, 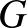 injektivitása azt eredményezné, hogy nincs megfelelő téglalap – vegyük észre, hogy most a második koordináta egy komplex szám (alkalmas hatványa), így
injektivitása azt eredményezné, hogy nincs megfelelő téglalap – vegyük észre, hogy most a második koordináta egy komplex szám (alkalmas hatványa), így 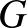 két pontban való egyezősége nemcsak a szakaszok hosszát teszi egyenlővé, de információt ad a lehetséges bezárt szögükről is. Persze a projektív sík
két pontban való egyezősége nemcsak a szakaszok hosszát teszi egyenlővé, de információt ad a lehetséges bezárt szögükről is. Persze a projektív sík 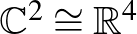 -be már beágyazható, így a korábbi ellentmondás itt nem várható. Itt következik Hugelmeyer másik ötlete: a beágyazást egy a
-be már beágyazható, így a korábbi ellentmondás itt nem várható. Itt következik Hugelmeyer másik ötlete: a beágyazást egy a 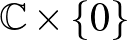 egy kis környezetének
egy kis környezetének  peremével (ami az
peremével (ami az 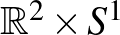 háromdimenziós térrel azonosítható) elmetszve egy csomót kapunk, amely egy Möbius-szalagot határol. Ezt a csomót (a Möbius-szalagjával együtt) aztán úgy tudja az
háromdimenziós térrel azonosítható) elmetszve egy csomót kapunk, amely egy Möbius-szalagot határol. Ezt a csomót (a Möbius-szalagjával együtt) aztán úgy tudja az 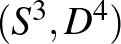 (a háromdimenziós gömb és az általa határolt négydimenziós golyó) párba beágyazni, hogy a
(a háromdimenziós gömb és az általa határolt négydimenziós golyó) párba beágyazni, hogy a 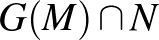 metszet olyan csomóba képződik, amely nem határol Möbius-szalagot a négydimenziós térben. Az utóbbi állítást (nevezetesen, hogy egy, a háromdimenziós térben lévő csomó nem határol beágyazott Möbius-szalagot a négydimenziós térben) nem is olyan egyszerű belátni. Erre igazán effektív módszert J. Batson talált 2013-ban [1], majd (hasonló, csomó Floer homológiai módszereket alkalmazva) Ozsváth, Szabó, és a jelen írás szerzője fejlesztették módszerét tovább [7].
metszet olyan csomóba képződik, amely nem határol Möbius-szalagot a négydimenziós térben. Az utóbbi állítást (nevezetesen, hogy egy, a háromdimenziós térben lévő csomó nem határol beágyazott Möbius-szalagot a négydimenziós térben) nem is olyan egyszerű belátni. Erre igazán effektív módszert J. Batson talált 2013-ban [1], majd (hasonló, csomó Floer homológiai módszereket alkalmazva) Ozsváth, Szabó, és a jelen írás szerzője fejlesztették módszerét tovább [7].
A 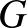 definíciójában a második koordinátában levő kitevőt azért választottuk 6-nak, hogy épp a
definíciójában a második koordinátában levő kitevőt azért választottuk 6-nak, hogy épp a  oldalarányú téglalapokra vonatkozó eredmény jöjjön ki; magasabb páros kitevők választásával hasonló (de gyengébb) eredmények következnek.
oldalarányú téglalapokra vonatkozó eredmény jöjjön ki; magasabb páros kitevők választásával hasonló (de gyengébb) eredmények következnek.
4. A téglalapos cövek sejtés megoldása
A fenti okoskodást további (nagyon komoly felkészülést igénylő) technikákkal ötvözve Joshua Greene és Andrew Lobb [3] látta be a következő tételt, pontot téve a téglalapos cövek probléma erős változatának sima esete végére.
Tétel (Greene–Lobb, [3]): Legyen 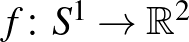 egy sima Jordan-görbe, és legyen
egy sima Jordan-görbe, és legyen 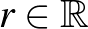 pozitív szám. Ekkor van
pozitív szám. Ekkor van  -ben négy olyan
-ben négy olyan 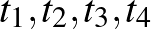 pont, hogy képük egy olyan téglalapot határoz meg, melyre az oldalak aránya épp
pont, hogy képük egy olyan téglalapot határoz meg, melyre az oldalak aránya épp 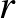 .
.
Bizonyításuk mélyén egy új technika lapul, ami azon alapszik, hogy Hugelmeyer Möbius-szalagból 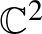 -be mutató leképezésének képterét szimplektikus sokaságnak tekintik. (Egy
-be mutató leképezésének képterét szimplektikus sokaságnak tekintik. (Egy 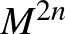
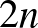 -dimenziós sokaságon egy szimplektikus struktúra nem más, mint egy zárt, nemelfajuló 2-forma, vagyis egy olyan
-dimenziós sokaságon egy szimplektikus struktúra nem más, mint egy zárt, nemelfajuló 2-forma, vagyis egy olyan 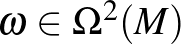 , amelyre
, amelyre 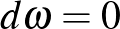 és
és 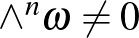 teljesül.) A szimplektikus topológia és geometria a matematika egy fiatal ága, és komplex analitikus eszközök továbbfejlesztésével speciális, a szimplektikus struktúrát is figyelembe vevő leképezéseket vizsgál. Ezen eszközök segítségével lehet megmutatni például azt, hogy a Klein-kancsó (mely
teljesül.) A szimplektikus topológia és geometria a matematika egy fiatal ága, és komplex analitikus eszközök továbbfejlesztésével speciális, a szimplektikus struktúrát is figyelembe vevő leképezéseket vizsgál. Ezen eszközök segítségével lehet megmutatni például azt, hogy a Klein-kancsó (mely 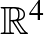 -be beágyazható) nem ágyazható be a szimplektikus
-be beágyazható) nem ágyazható be a szimplektikus 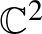 -be mint Lagrange-féle részsokaság. (Egy
-be mint Lagrange-féle részsokaság. (Egy 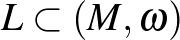 szimplektikus sokaság-beli
szimplektikus sokaság-beli 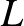 részsokaság Lagrange-féle, ha
részsokaság Lagrange-féle, ha 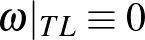 .) A fenti fogalmak bőven a jelen dolgozat keretein túl mutatnak, bemutatásukra itt nincs lehetőség, de talán felemlegetésük és az itt tárgyalt egyszerű(nek látszó) probléma megoldásában játszott szerepük alapján felkeltik a kedves olvasó érdeklődését.
.) A fenti fogalmak bőven a jelen dolgozat keretein túl mutatnak, bemutatásukra itt nincs lehetőség, de talán felemlegetésük és az itt tárgyalt egyszerű(nek látszó) probléma megoldásában játszott szerepük alapján felkeltik a kedves olvasó érdeklődését.
Irodalomjegyzék
- [1] J. Batson: Nonorientable slice genus can be arbitrarily large, Math. Res. Lett. 21 (2014), no. 3, 423–436.
[2] A. Emch: Some properties of closed convex curves in a plane, Amer. J. Math. 35 (1913), 407–412.
[3] J. Greene, A. Lobb: The Rectangular Peg Problem, arXiv:2005.09193
[4] C. Hugelmeyer: Every smooth Jordan curve has an inscribed rectangle with aspect ratio equal to  , arXiv:1803.07417
, arXiv:1803.07417
[5] B. Matschke: A survey on the square peg problem, Notices Amer. Math. Soc. 61 (2014), no. 4, 346–352.
[6] M. Meyerson: Balancing acts, Topology Proc. 6 (1981), no. 1, 59–75.
[7] P. Ozsváth, Z. Szabó, A. Stipsicz: Unoriented knot Floer homology and the unoriented four-ball genus, Int. Math. Res. Not. IMRN 2017, 17, 5137–5181.
[8] L. Schnirelman: On some geometric properties of closed curves, (in Russian) Usp. Mat. Nauk 10 (1944), 34–44.
[9] T. Tao: An integration approach to the Toeplitz square peg problem, Forum Math. Sigma 5 (2017), Paper No. e30, 63 pp.
[10] O. Toeplitz: Über einige Aufgaben der Analysis situs, Verhandlungen der Schweizerischen Naturforschenden Gesellschaft in Solothurn 4 (1911), 197.
5. Appendix: a Greene–Lobb bizonyítás alapelemei
Nem nehéz megadni a Greene–Lobb tételben szereplő függvényeket sem. Lássuk el a 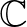 komplex egyenest a szokásos
komplex egyenest a szokásos 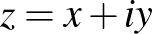 valamint a
valamint a 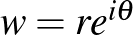 polárkoordinátákkal. Ekkor
polárkoordinátákkal. Ekkor 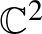 -en az
-en az 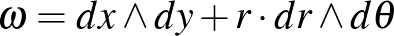 forma adja majd a megkívánt szimplektikus formát. Adjuk meg az
forma adja majd a megkívánt szimplektikus formát. Adjuk meg az 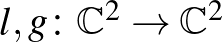 függvényeket az
függvényeket az
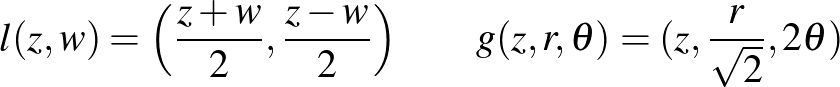
formulákkal. Legyen 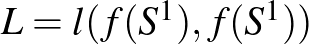 tórusz, és legyen
tórusz, és legyen  ennek
ennek 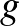 -menti képe. Nem nehéz látni, hogy
-menti képe. Nem nehéz látni, hogy  pontosan akkor, ha
pontosan akkor, ha 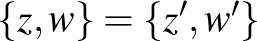 , vagyis
, vagyis  továbbra is egy Möbius-szalag.
továbbra is egy Möbius-szalag.
Vegyük az 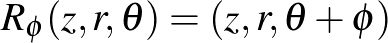 leképezést, mely tehát
leképezést, mely tehát 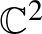 -ből
-ből 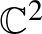 -be mutat. Megmutatható, hogy
-be mutat. Megmutatható, hogy  és
és 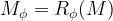 a peremüktől különböző metszéspontjai épp olyan, az
a peremüktől különböző metszéspontjai épp olyan, az 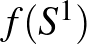 görbébe írt tégalapoknak felelnek meg, amelyekre az átlók által bezárt szög épp
görbébe írt tégalapoknak felelnek meg, amelyekre az átlók által bezárt szög épp 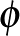 . (Téglalapok hasonlósága az átlók bezárt szögével is megragadható.)
. (Téglalapok hasonlósága az átlók bezárt szögével is megragadható.)
Ha azonban  és
és 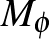 valamilyen
valamilyen 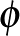 -re nem metszik egymást a peremükön kívül, akkor az
-re nem metszik egymást a peremükön kívül, akkor az 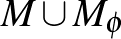 unió egy beágyazott Klein-kancsót ad. (A simasághoz a perem mentén simítani kell, ami egy messze nem triviális, lokális modellen való számítást igényel.)
unió egy beágyazott Klein-kancsót ad. (A simasághoz a perem mentén simítani kell, ami egy messze nem triviális, lokális modellen való számítást igényel.)
Annak belátása, hogy az 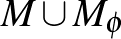 Klein-kancsó (illetve simítása) Lagrange-féle, még nem nehéz. Annak belátása azonban, hogy a szimplektikus
Klein-kancsó (illetve simítása) Lagrange-féle, még nem nehéz. Annak belátása azonban, hogy a szimplektikus  térben nincs beágyazott Lagrange-féle Klein-kancsó, nagyon komoly technikai előkészületeket igényel.
térben nincs beágyazott Lagrange-féle Klein-kancsó, nagyon komoly technikai előkészületeket igényel.
Stipsicz András, Rényi Alfréd Matematikai Kutatóintézet









