Klein-gyöngyök

Az emberiséget hosszú idő óta elbűvölik a különféle szimmetriákat megjelenítő, ismétlődő motívumok. Bolyai János (1802–1860) magyar matematikus és hadmérnök 1823. évi felfedezése, a hiperbolikus geometria megszületése fordulópontot hozott a 19. század matematikájában. Ez a felfedezés sokkal gazdagabb mintázatokat tett lehetővé. Közülük néhányat a holland grafikus, Maurits Cornelis Escher (1898–1972) népszerűsített a híres Circle Limit (Körhatár) fametszet-sorozatában, amelyen a Poincaré-féle körmodellt csempézte ki periodikus mintákkal. A hiperbolikus sík körmodellje nevét Jules Henri Poincaréről (1854–1912) kapta. Számítógép segítségével nem nehéz escher-szerű képeket létrehozni. Szimmetriáról hagyományosan az euklideszi transzformációk – eltolás, forgatás, tükrözés – alkalmazásakor beszélünk. Szimmetria azonban olyan leképezések alkalmazása során is előáll, mint a Möbius-transzformációk, amelyekkel torzítás, nyújtás, csavarás valósítható meg. 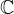-vel jelölve a komplex számok halmazát, az

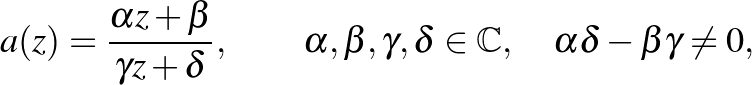
$\displaystyle a(z)=\frac{\alpha z+\beta}{\gamma z+\delta},\qquad \alpha, \beta, \gamma, \delta \in \mathbb{C},\quad \alpha \delta - \beta \gamma \neq 0,$

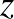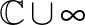alakú leképezést, ahol $z$ a $\mathbb{C} \cup \infty$ Riemann-gömb eleme, Möbius-transzformációnak nevezzük, August Ferdinand Möbius (1790–1868) emlékére. A Riemann-gömb Georg Friedrich Bernhard Riemann (1826–1866) nevét őrzi. Az ilyen transzformációk az 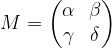alakú mátrixokkal reprezentálhatók. Nem távolságtartók, de megőrzik a szögeket és a Riemann-gömb bármely körét a Riemann-gömb egy körére képezik le (lásd [1] Állítás 8.2, 34. o.). Továbbá előállnak a 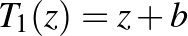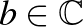$T_1(z)=z+b$ , $b \in \mathbb{C}$ , eltolás, a 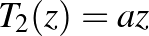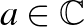$T_2(z)=a z$ , $a \in \mathbb{C}$ , origó körüli forgatva nyújtás és 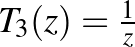$T_3(z)=\frac{1}{z}$ leképezések kompozíciójaként. A 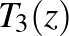$T_3(z)$ leképezés a 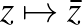$z \mapsto \bar{z}$ komplex konjugáció, azaz a valós tengelyre való tükrözés és a 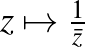$z \mapsto \frac{1}{\bar{z}}$ leképezés, azaz az origó középpontú egység sugarú körre vonatkozó inverzió kompozíciója. Az 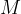mátrix nyoma 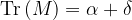. A Möbius-leképezéseket az őket leíró mátrix nyoma szerint a loxodromikus, az elliptikus és a parabolikus leképezések osztályába sorolhatjuk. A loxodromikus leképezéseknek két fixpontjuk van, amelyeket forrás és nyelő fixpontnak nevezzünk. Ilyen leképezések hatására a pontok spirális pályán futnak a leképezés forrás fixpontjából kiindulva a nyelő fixpont felé. Minden loxodromikus leképezés egy 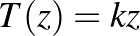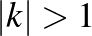$T(z)=k z$ , $\vert k\vert >1$ leképezés konjugáltja. A loxodromikus leképezéseket leíró mátrix nyoma egy $\mathbb{C} \setminus [-2,2]$ -beli szám. Azokat a Möbius-transzformációkat, amelyeknek egyetlen fixpontjuk van, azaz a forrás és a nyelő fixpontjuk egybeesik, parabolikusnak nevezzük. 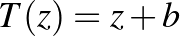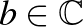Minden parabolikus leképezés egy $T(z)=z+b$ , $b \in \mathbb{C}$ , eltolás konjugáltja. A parabolikus leképezésekhez tartozó mátrix nyoma 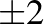$\pm 2$ (lásd [3] 3. fejezetében).

Ebben az írásban egy rövid ismertetést szeretnék adni egy olyan mintázatról, amely invariáns marad egy 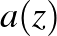$a(z)$ -vel jelölt loxodromikus és egy 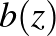$b(z)$ -vel jelölt parabolikus transzformáció által generált 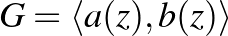$G=\langle a(z), b(z) \rangle$ csoport hatására nézve. A 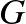$G$ csoportban az összes lehetséges transzformációt meg lehet adni egy „szóval”, ábécéként az 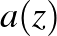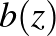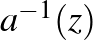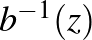$a(z)$ , $b(z)$ , $a^{-1}(z)$ , $b^{-1}(z)$ betűket használva. 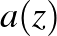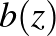Ezt nevezzük az $a(z)$ és $b(z)$ által generált Schottky-csoportnak, Friedrich Hermann Schottky (1851–1935) emlékére. 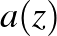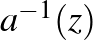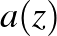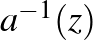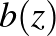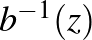Ha egy szóban az $a(z)$ elem közvetlenül az inverze, $a^{-1}(z)$ , mellett szerepel, akkor a szó leegyszerűsíthető az $a(z)$ , $a^{-1}(z)$ pár elhagyásával, és hasonlóan a $b(z)$ és a $b^{-1}(z)$ pár esetén. Így a 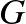$G$ csoport szabad csoport (lásd [1] 23.3 Tétel, 92. o., és [3] 4. fejezetében).

1.ábra

Az 1. ábrán látható fekete csipkemotívum a 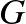$G$ csoport „határpontjainak” a halmaza. Határpont alatt azokat a pontokat értjük, amelyeket megközelíthetünk, ha valamely más pontra alkalmazzuk 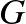$G$ -beli leképezések egy végtelen sorozatát. Az euklideszi tapétázásoknak csak egy határpontja van. Escher Körhatár munkáinak határpontjai egy kört alkotnak (lásd [1] 50.o.). Az általunk vizsgált fenti mintázat határpontjainak halmaza végtelen sok körből és ezek torlódási pontjaiból áll (lásd 1. ábra).

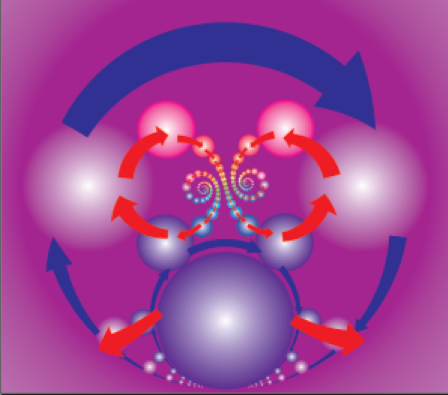
2. ábra

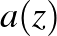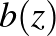Az $a(z)$ és $b(z)$ leképezések hatását a 2. ábra mutatja be, amelyen az 1. ábra egy véges részlete, egymást érintő körlapok láthatók. Az 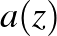$a(z)$ transzformáció az ibolya színű körlemezeket mozgatja balról jobbra, egyikről a következőre a piros nyilak irányába. Az 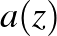$a(z)$ transzformáció loxodromikus, a pontokat egy végtelen dupla spirálon mozgatja a forrás fixpontból a nyelő fixpont irányába.

A 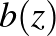$b(z)$ transzformáció, melynek hatására a mozgást a kék nyilak jelölik, a két világoskék körlemezt invariánsan hagyja. A 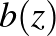$b(z)$ leképezés egyetlen fixpontja a két kék kör érintési pontja. Így 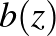$b(z)$ egy parabolikus leképezés, a pontokat a fixpontjából induló kör alakú pályákon mozgatja, azokon az óramutató járásával megegyező irányba haladva. A hozzá tartozó mátrix nyoma 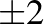$\pm 2$ . Mátrixok nyomára vonatkozó azonosságok felhasználásával (lásd [3] 6. 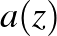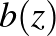fejezetében) ez egy polinomiális összefüggést ad az $a(z)$ és a $b(z)$ generátorokra.

A 2. ábrán látható körháló komplementere négy fehér tartomány, ezeket a képen 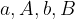jelöli. Az 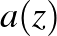$a(z)$ leképezés az 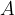tartományt határoló köröket mozgatja az 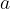tartományt határoló körökbe, és hasonlóan mozgatja a 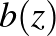$b(z)$ transzformáció 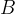a és a 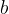tartományokat határoló köröket. Az 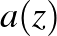$a(z)$ leképezés a 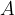tartomány külsejét az 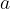tartomány belsejére képezi le és hasonlóan a 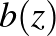$b(z)$ leképezés a 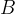tartomány külsejét a 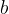tartomány belsejére képezi le. 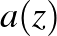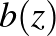Az $a(z)$ és a $b(z)$ leképezéseket ismételve, egymásba ágyazott tartományok sorozatát kapjuk. Az egymásba ágyazott tartományok torlódási pontjai alkotják a Schottky-csoport határhalmazát.

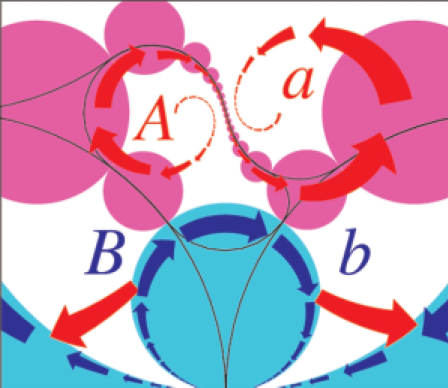
3.ábra

A 3. ábrán a körlemezek közötti transzformációkat jelképező nyilak zárt hurkait látjuk. Követve a nyilakat, melyek az 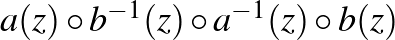$a(z) \circ b^{-1}(z) \circ a^{-1}(z) \circ b(z)$ leképezések kompozícióját mutatják – először egy kék nyíl hat előre a nyíl irányába [ 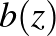$b(z)$ ], utána egy piros nyíl hat a nyíllal ellenkező irányba [ 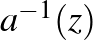$a^{-1}(z)$ ], aztán egy kék nyíl hat visszafelé [ 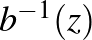$b^{-1}(z)$ ], végül egy piros nyíl előre [ 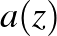$a(z)$ ] –, azt látjuk, hogy ez a transzformáció invariánsan hagyja a nagy külső „körlemezt”, azaz az 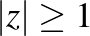$\vert z\vert \ge 1$ pontok halmazát, mely tartalmazza 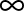$\infty$ -t. Ezt 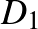$D_1$ -gyel fogjuk jelölni. Ugyancsak invariánsan hagyja a bal oldali legnagyobb fehéreslila körlemezt. Ezt jelöljük 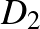$D_2$ -vel. Ebből adódik, hogy az 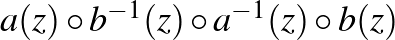$a(z) \circ b^{-1}(z) \circ a^{-1}(z) \circ b(z)$ leképezés is parabolikus transzformáció. Így az 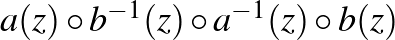$a(z) \circ b^{-1}(z) \circ a^{-1}(z) \circ b(z)$ leképezéshez tartozó mátrix nyoma ismét 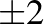$\pm 2$ . Ha feltesszük, hogy 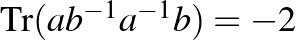$\operatorname{Tr}(ab^{-1}a^{-1}b)=-2$ , akkor a mátrixok nyomára vonatkozó

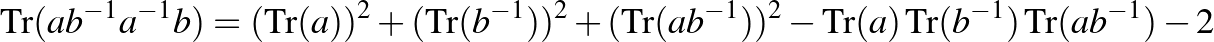
$\displaystyle \operatorname{Tr}(ab^{-1}a^{-1}b)=(\operatorname{Tr}(a))^2+(\oper... ...2-\operatorname{Tr}(a) \operatorname{Tr}(b^{-1}) \operatorname{Tr}(ab^{-1})-2$

azonosság a

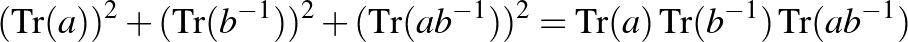
$\displaystyle (\operatorname{Tr}(a))^2+(\operatorname{Tr}(b^{-1}))^2+(\operator... ...)^2=\operatorname{Tr}(a) \operatorname{Tr}(b^{-1}) \operatorname{Tr}(ab^{-1})$

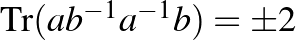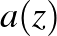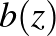Markov-azonossággá egyszerűsödik, amely Andrej Andrejevics Markov (1856–1922) nevét őrzi. Így a $\operatorname{Tr}(ab^{-1}a^{-1}b)=\pm 2$ feltétel újabb polinomiális összefüggést ad az $a(z)$ és a $b(z)$ traszformációk között. 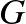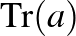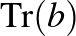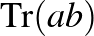A mátrixok nyomára vonatkozó azonosságok alkalmazása lehetővé teszi, hogy a $G$ csoport minden „szavának” nyomát kifejezhessük a $\operatorname{Tr}(a)$ , $\operatorname{Tr}(b)$ és a $\operatorname{Tr}(ab)$ nyomok segítségével (lásd [3] 6. fejezet, 189–192. o.).

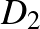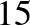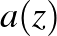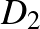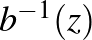Továbbá ha $D_2$ -nél kezdünk, és pontosan $15$ -ször alkalmazzuk egymás után az $a(z)$ -t (a piros nyilakkal jelölt transzformációkat a nyilak irányában), akkor a jobb oldali szimmetrikusan elhelyezkedő legnagyobb fehéreslila körlemezhez érkezünk. És innen visszaugorhatunk $D_2$ -re a $b^{-1}(z)$ leképezés hatására (a kék nyíl által jelölt leképezést egyszer visszafelé, a nyíllal ellenkező irányban alkalmazva). Ugyanez a kompozíció invariánsan hagyja az 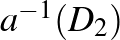$a^{-1}(D_2)$ körlemezt, melyet éppen egy piros nyíl hatása képez 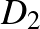$D_2$ -re. 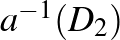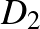(Az $a^{-1}(D_2)$ a $D_2$ -t kívülről érintő kékesfehér körlemez.) Ezért 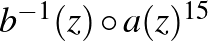$b^{-1}(z) \circ a(z)^{15}$ is parabolikus leképezés. 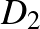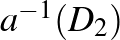Fixpontja a $D_2$ és az $a^{-1}(D_2)$ körlemezek érintési pontja. A 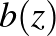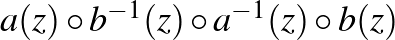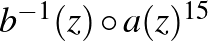$b(z)$ , $a(z) \circ b^{-1}(z) \circ a^{-1}(z) \circ b(z)$ , $b^{-1}(z) \circ a(z)^{15}$ parabolikus leképezések által adott polinomiális feltételek (konjugálás erejéig) egyértelműen meghatározzák a mintázatot.

A körlemezek színezése a következőképpen történik: A 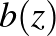$b(z)$ leképezés alkalmazása nem változtatja meg a színt. Az 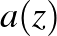$a(z)$ leképezést alkalmazva a körlemez színe a következő színre vált 15 szín ciklusában.

A 4. ábra a körlemezeknek a 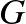$G$ hatására vonatkozó két ekvivalenciaosztályát mutatja.

4.ábra

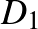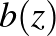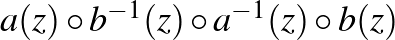Ez kiterjeszti a körlemezek színezését az eredeti körhálóban. Minden körlemez invariáns a transzformációk egy részcsoportjának hatásával szemben. Például láttuk, hogy a $D_1$ külső körlemez invariáns marad a $b(z)$ és az $a(z) \circ b^{-1}(z) \circ a^{-1}(z) \circ b(z)$ leképezések hatására. Ez a két szó generálja a 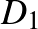$D_1$ körlemez stabilizátor részcsoportját. Ebben a részcsoportban az összes szó olyan, hogy a bennük előforduló 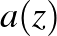$a(z)$ kifejezések kitevőinek az összege 0. Így a 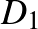$D_1$ körlemez képének a színét a 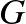$G$ csoport szavainak hatására éppen a szavakban levő 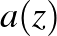$a(z)$ kifejezések kitevőinek az összege határozza meg.

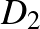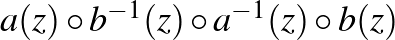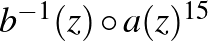Hasonlóan a $D_2$ körlemez stabilizátora az $a(z) \circ b^{-1}(z) \circ a^{-1}(z) \circ b(z)$ és a $b^{-1}(z) \circ a(z)^{15}$ leképezések által van generálva. Ezen részcsoport minden szavában az 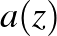$a(z)$ kitevőinek az összege 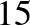$15$ többszöröse. Ennélfogva a színezésünk konzisztens, ha 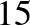$15$ színt használunk.

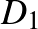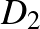A teljes mintázaton keresztül a következő szabályt látjuk: Ha a $D_1$ és a $D_2$ körlemez színét ugyanannak választjuk, akkor két érintő körlemez pontosan akkor tartozik különböző ekvivalenciaosztályhoz, ha ugyanaz a színük. Az ekvivalenciaosztályok a 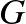$G$ csoport egy 2 indexű részcsoportjához tartoznak.

Ha kinagyítjuk a kép közepét, az 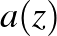$a(z)$ transzformáció fixpontjai mintha szemek lennének (lásd az 5. ábrát).

5.ábra

Az olyan csoportot, amelynek a határhalmaza kör, Fuchs-féle csoportnak nevezzük. A csoport elnevezése Immanuel Lazarus Fuchs (1833–1902) emlékét őrzi. Möbius-transzformációk egy csoportját, amelyek határhalmaza egy összefüggő hurok, kvázifuchs-féle csoportnak nevezzük. A 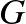$G$ csoportot azért hívja David J.Wright „dupla csúcsú csoportnak” [4] cikkében, mert ez utal arra, hogy 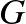$G$ kétgenerátorú kvázifuchs-féle csoportok extrém „deformációja” (lásd [3] 6. és 9. fejezeteit).

Hasonló tulajdonságú csoportokról és határhalmazukról Felix Cristian Klein (1849-1925) kutatásai úttörő jelentőséggel bírnak. Ez motiválta ennek az írásnak a címét. Munkássága során Klein fizikailag is vizualizált szimmetrikus mintázatokat. Azonban a határhalmaz ábrázolása olyan nehézségekkel szembesítette, amelyekről 1894-ben így írt (lásd [2]):

„A kérdés az, hogy milyen konfigurációt alkot a körök összessége és hogy mi lesz a határpontjaiknak a halmaza. Ezekre a kérdésekre nem nehéz választ adni tisztán logikai úton; de az érzékeltetésükben úgy látszik, meghiúsul a teljesség, ha megpróbáljuk az eredményt képként ábrázolni.”

További mintázatok elemzése és a számítógépes vizualizációjukhoz szükséges programok találhatók [3]-ban.

Ebben a cikkben az összes ábra szerzői joga David J. Wrightot illeti, aki David Mumforddal közösen írt „kleini” programukkal állította elő azokat, és újraközlésüket az Érintő számára engedélyezte.

Irodalomjegyzék

[1] T. K. Carne, Geometry and Groups, Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, https://www.dpmms.cam.ac.uk/~tkc/GeometryandGroups/GeometryandGroups.pdf

[2] F. Klein, Lectures on Mathematics, Amer. Math. Soc., 2000.

[3] D. Mumford, C. Series, and D. Wright, Indra's Pearls: The Vision of Felix Klein, Cambridge Univ. Press, 2002.

[4] D. Wright, Double Cusp Group, Notices of the AMS, 51, no. 11 (2004), 1332–1333.

https://www.ams.org/notices/200411/comm-wright.pdf

Figula Ágota
Debreceni Egyetem, Természettudományi és Technológiai Kar,
Matematikai Intézet, Debrecen

A munkát a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal (NKFI) K132951 és az EFOP-3.6.1-16-2016-00022 projekt támogatta. A második projektet az Európai Unió és az Európai Szociális Alap finanszírozza.