Az érintőmódszer történetéről

Hosszú évek óta tanítok matematikatörténetet, de mindig tanulok valami újat. A napokban láttam a Netflixen egy filmet, 21 – Las Vegas ostroma, amelyben elhangzott egy abszurd állítás: Newton ellopta az érintőmódszert Raphsontól. Kicsit utánanéztem a történetnek. A magyar nyelvű wikipédia Newton-módszer szócikke a lényeget vázolja, de számomra nem eléggé érthetően. Az ott ajánlott [2] forrás segítségével sikerült a lényeget megértenem, és ez alapján tájékoztatom az Érintő olvasóit.

A közfelfogás szerint (amit eddig én is elfogadtam) a nemlineáris egyenletek numerikus megoldásának új korszakát nyitotta meg a Newton-féle érintőmódszer (1671).

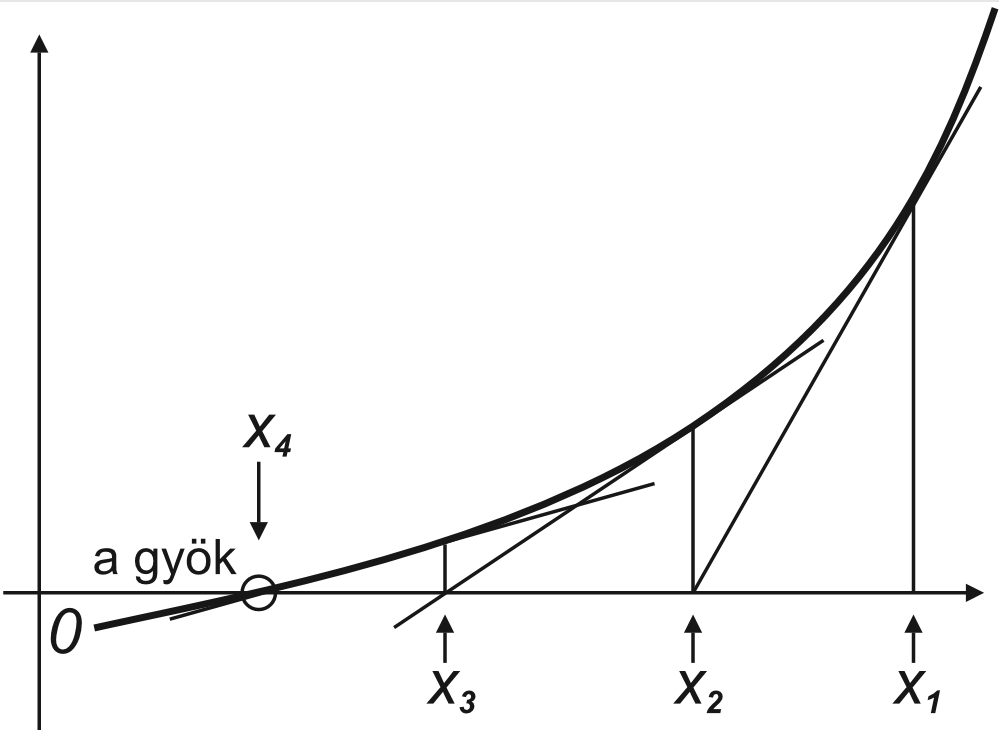1. ábra. Az érintőmódszer működése

Ha 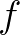$f$ skalár–skalár függvény, amelynek 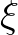$\xi$ gyöke, azaz 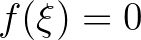$f(\xi)=0$ , akkor egy közelítő 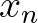$x_n$ gyök ismeretében megpróbálkozhatunk az érintőegyenes 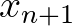$x_{n+1}$ metszéspontját adó 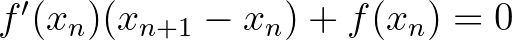$f'(x_n)(x_{n+1}-x_n)+f(x_n)=0$ egyenletből adódó

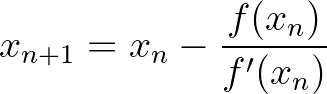
$\displaystyle x_{n+1}=x_n-{{f(x_n) }\over {f'(x_n)}}$

iterációval. Ez a módszer nem mindig konvergál, de jó esetben nemcsak konvergál, hanem nagyon gyorsan konvergál. Ha nem ismerjük a függvény deriváltját, akkor a következő közelítéssel élhetünk:

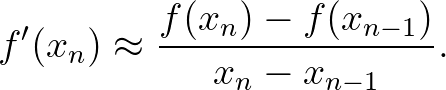
$\displaystyle f'(x_n)\approx \frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}.$

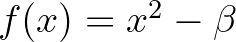A legegyszerűbb alkalmazás a $\beta>0$ szám négyzetgyökének megkeresése, ekkor $f(x)=x^2-\beta$ :

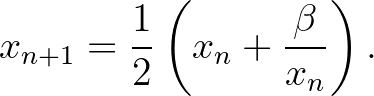
$\displaystyle x_{n+1}=\frac{1}{2}\left(x_n+\frac{\beta}{x_n}\right).$

Külön érdekesség, hogy ezt a módszert már az ókori babilóniaiak is ismerték [1]. Vélhetőleg ennek segítségével határozta meg Arkhimédész $\sqrt{3}$ jó közelítő értékét i.e. 240 körül, amikor az egységátmerőjű kör kerületét szoros alsó–felső korlátok közé szorította.

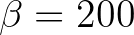A valóság azonban bonyolultabb, és visszavezet az 1960-as években még a középiskolában oktatott speciális négyzetgyökvonási algoritmushoz, amelyet a matematikatörténet Vieta nevéhez fűz (1600 előtt). Az egyszerűség kedvéért itt is a babiloni $\sqrt{2}$ -es példát vesszük, és a 100-szoros $\beta=200$ -zal folytatjuk. 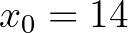Kezdő lépésként egy olyan természetes számot választunk, amely alulról jól közelíti a $\sqrt{200}$ -at: $x_0=14$ , amelynek négyzete 196.

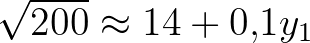Ahhoz, hogy pontosítsuk ezt a becslést, jelölje az első tizedesjegyet $y$ , azaz $\sqrt{200}\approx 14+0{,}1y_1$ -gyel próbálkozunk. Elvégezve a négyzetre emelést, a 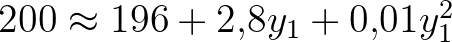$200\approx 196+2{,}8y_1+0{,}01y_1^2$ közelítést kapjuk, amelyből eldobjuk a négyzetes tagot, és csak az első értékes jegyet tartjuk meg:

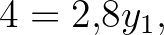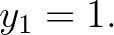
$\displaystyle 4=2{,}8y_1,$ azaz $\displaystyle y_1=1.$

Még egy lépéssel tovább lépünk: 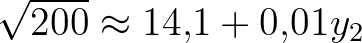$\sqrt{200}\approx 14{,}1+0{,}01y_2$ , azaz újbóli négyzetreemeléssel

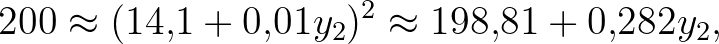
$\displaystyle 200\approx (14{,}1+0{,}01y_2)^2\approx 198{,}81+0{,}282y_2,$

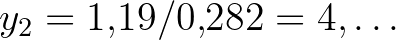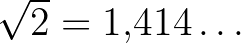azaz $y_2=1{,}19/0{,}282=4{,}\dots$ . A közelítő eredmény $\sqrt{2}=1{,}414\dots$ .

Sem Newton 1671-ben, sem Raphson 1690-ben nem tudott elszakadni a Vieta-módszer algebrai hatókörétől, bár ők nem ragaszkodtak a tizedesjegyek egymás utáni meghatározásához. Valóban, a fenti módszerben már az első közelítésben megkaphattuk volna a 0,14-ot.

A korra jellemző, hogy nem általános, hanem speciális polinomokat vizsgáltak, mi azonban kedvelt harmadfokú egyenletüket paraméteresen írjuk föl:

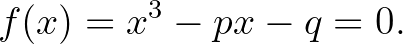
$\displaystyle f(x)=x^3 -px-q=0.$

Itt a fokozatos megközelítésnél nincs szükség explicit deriválásra, elegendő az 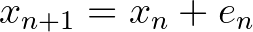$x_{n+1}=x_n+e_n$ lineáris közelítése:

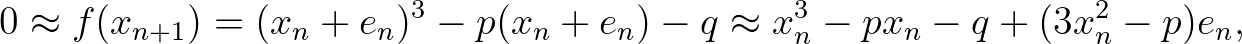
$\displaystyle 0\approx f(x_{n+1})=(x_n+e_n)^3 -p(x_n+e_n)-q\approx x_n^3-px_n-q+(3x_n^2-p)e_n,$

azaz

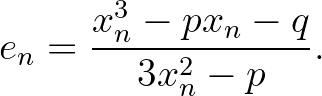
$\displaystyle e_n=\frac{x_n^3-px_n-q}{3x_n^2-p}.$

Csak az 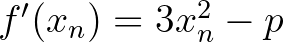$f'(x_n)=3x_n^2-p$ (és az 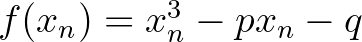$f(x_n)=x_n^3-px_n-q$ ) jelölés bevezetésével kapjuk meg az érintőmódszert.

A Principia III. kiadásában (1726-ban) a Kepler-feladat megoldásával kapcsolatban Newton nem algebrai egyenletet is megoldott módszerével, ez azonban 1882-ig észrevétlenül maradt. Ezt leszámítva, mindkét szerző kizárólag polinomiális egyenletekre szorítkozott.

2. ábra. Godfrey Kneller festménye: IsaacNewton –1689 (Forrás:https://hu.wikipedia.org/w/index.php?title=Isaac_Newton&oldid=23210874)

Simpson volt az első (neve az integrálási szabályáról maradt fenn), aki 1740-ben nem algebrai (négyzetgyökös) függvényeket vizsgált, és a levezetésnél explicite differenciálta a függvényeket. De az igazi érintőmódszert, az általunk is alkalmazott jelöléssel csak Lagrange publikálta 1798-ban, ő Newton mellett még Raphson nevét is megemlítette. Fourier 1831-ben már csak Newtonra hivatkozott, és ez okozhatta azt, hogy Raphsont és Simpsont sokáig elfeledték.

3. ábra. Raphson aláírása felvételekor a Királyi Társaságba (Forrás: https://commons.wikimedia.org/wiki/File:Raphson.gif)

Zárásként megemlítjük, hogy bár Newton valóban évtizedekkel Raphson után publikálta kezdetlegesebb módszerét, nem lopott el semmit sem Raphsontól, és nem is volt köztük prioritási vita. De a matematika vonzerejét mutatja, hogy hollywoodi filmekben is megjelennek komoly matematikai problémák, még ha időnként eltorzítva is.

Irodalomjegyzék

: [1] Boyer, C. B. (1968): A History of Mathematics, Princeton, Princeton University Press. Kiegészített kiadás: Revised by Uta C. Merzbach (1991), Wiley.

[2] Ypma, T. (1995): Historical development of the Newton–Raphson-method, SIAM Review, 37:4, 531–551.

Simonovits András