Ebben az írásban egy rövid bevezetést szeretnék adni azokhoz a fogalmakhoz és állításokhoz, amelyek a méhkaptár-modell felhasználásával a Horn-sejtés egy bizonyításához vezetnek. Az 1. tételben megadjuk a hermitikus mátrixok és összegmátrixuk sajátértékei közötti kapcsolat átfogalmazását egy síkbeli problémára, a méhkaptár-modellre.
1912-ben Hermann Weyl fogalmazta meg a következő kérdést: Legyen ![]() és
és ![]() két
két ![]() -es hermitikus mátrix. Hogyan lehet az
-es hermitikus mátrix. Hogyan lehet az ![]() összeg összes lehetséges sajátértékeinek halmazát meghatározni az
összeg összes lehetséges sajátértékeinek halmazát meghatározni az ![]() és
és ![]() sajátértékeinek ismeretében?
sajátértékeinek ismeretében?
Ha ![]() , akkor az
, akkor az ![]() mátrix sajátértéke az
mátrix sajátértéke az ![]() és a
és a ![]() mátrix sajátértékeinek összege. Jelöljük egy
mátrix sajátértékeinek összege. Jelöljük egy ![]() -es hermitikus mátrix sajátértékeit valós számok egy monoton csökkenő
-es hermitikus mátrix sajátértékeit valós számok egy monoton csökkenő ![]() -esével,
-esével, ![]() -nel. Például a
-nel. Például a ![]() sajátértékeket
sajátértékeket ![]() -vel. Az
-vel. Az ![]() ,
, ![]() és
és ![]() mátrix sajátértékeit pedig rendre a
mátrix sajátértékeit pedig rendre a ![]() ,
, ![]() és
és ![]()
![]() -esekkel, így
-esekkel, így ![]() a második legnagyobb sajátértéke
a második legnagyobb sajátértéke ![]() -nak, stb. Könnyen kaphatunk szükséges feltételeket a
-nak, stb. Könnyen kaphatunk szükséges feltételeket a ![]() ,
, ![]() ,
, ![]() hármasra. Például: az
hármasra. Például: az ![]() mátrix nyoma egyenlő az
mátrix nyoma egyenlő az ![]() és a
és a ![]() mátrix nyomainak összegével, így kapjuk azt a feltételt, hogy
mátrix nyomainak összegével, így kapjuk azt a feltételt, hogy
Egy másik feltétel az, hogy
mivel az ![]() mátrix legnagyobb sajátértéke legfeljebb annyi, mint az
mátrix legnagyobb sajátértéke legfeljebb annyi, mint az ![]() és
és ![]() mátrixok legnagyobb sajátértékeinek az összege. Hasonló szükséges feltételeket, mint például
mátrixok legnagyobb sajátértékeinek az összege. Hasonló szükséges feltételeket, mint például
Weyl bizonyított. Ha ![]() , akkor a fenti feltételek szükségesek és elégségesek. Például ha az
, akkor a fenti feltételek szükségesek és elégségesek. Például ha az ![]() és a
és a ![]() mátrixok sajátértékei
mátrixok sajátértékei ![]() és
és ![]() , akkor az
, akkor az ![]() mátrix sajátértékei a
mátrix sajátértékei a ![]() ,
, ![]() , párok lesznek, de nem lehet például a
, párok lesznek, de nem lehet például a ![]() ,
, ![]() ,
, ![]() .
.
Magasabb dimenzióban más szükséges feltételek is vannak. Ezek mindegyike homogén lineáris egyenlőtlenség, és általánosan a minimax módszerrel vannak bebizonyítva. Ez a módszer azonban nem ad egy általános sémát, amellyel ezen egyenlőtlenségek egy szisztematikus és teljes listáját megkaphatnánk.
Alfred Horn 1962-ben megmutatta, hogy a szükséges feltételek egy teljes listája megadható az (1) által és a
formájú lineáris egyenlőtlenségek egy listája által, ahol ![]() és az összes
és az összes ![]() ,
, ![]() ,
, ![]() indexhármast egy bizonyos
indexhármast egy bizonyos ![]() véges halmazból választjuk. A probléma ezután a hármasok
véges halmazból választjuk. A probléma ezután a hármasok ![]() halmazainak a leírására redukálódott. Horn meghatározta ezt a
halmazainak a leírására redukálódott. Horn meghatározta ezt a ![]() halmazt
halmazt ![]() esetén és az általános esetben megmutatta, hogy az
esetén és az általános esetben megmutatta, hogy az ![]() indexekre teljesül a nyomfeltétel
indexekre teljesül a nyomfeltétel
és olyan lineáris egyenlőtlenségek, mint például ![]() . Ez vezetett a Horn sejtéshez (lásd: [2]):
. Ez vezetett a Horn sejtéshez (lásd: [2]):
Horn-sejtés: A ![]() halmaz megegyezik az összes
halmaz megegyezik az összes ![]() ,
, ![]() ,
, ![]() indexek halmazával, amely teljesíti (4)-et és
indexek halmazával, amely teljesíti (4)-et és
minden ![]() -re és minden
-re és minden ![]() -beli
-beli ![]() ,
, ![]() ,
, ![]() indexhármasokra.
indexhármasokra.
Ez a sejtés egy rekurzív algoritmust adna a ![]() halmazok generálására a korábbi
halmazok generálására a korábbi ![]() generátorok segítségével és így a Weyl-problémának egy teljes megoldásához vezetne minden dimenzióban. A Weyl-probléma újrafogalmazására a méhkaptár-modellt használva, és a Horn-sejtés egy bizonyítására 1999-ben A. Knutson és T. Tao [4] cikkében került sor.
generátorok segítségével és így a Weyl-problémának egy teljes megoldásához vezetne minden dimenzióban. A Weyl-probléma újrafogalmazására a méhkaptár-modellt használva, és a Horn-sejtés egy bizonyítására 1999-ben A. Knutson és T. Tao [4] cikkében került sor.
Most definiálni fogjuk a méhkaptárt és megadjuk a kapcsolatát Weyl feladatával. Az ![]() esetben a szükséges és elegendő feltételek halmaza
esetben a szükséges és elegendő feltételek halmaza ![]() -re, hogy
-re, hogy ![]() . Ennek az esetnek az analógiájára definiáljuk a
. Ennek az esetnek az analógiájára definiáljuk a
relációt, amely akkor áll fenn ha léteznek ![]() ,
, ![]() ,
, ![]() hermitikus mátrixok
hermitikus mátrixok ![]() sajátértékekkel úgy, hogy
sajátértékekkel úgy, hogy ![]() . Így a Weyl-probléma az (5) megoldáshalmazának a meghatározása. Azt mondjuk, hogy a
. Így a Weyl-probléma az (5) megoldáshalmazának a meghatározása. Azt mondjuk, hogy a
reláció teljesül, ha léteznek ![]() ,
, ![]() ,
, ![]() hermitikus mátrixok
hermitikus mátrixok ![]() sajátértékekkel úgy, hogy
sajátértékekkel úgy, hogy ![]() .
.
ahol ![]() . Ezért a Weyl-probléma megoldásához elégséges meghatározni az olyan
. Ezért a Weyl-probléma megoldásához elégséges meghatározni az olyan ![]() hármasok halmazát, amelyek teljesítik (6)-ot. A (6) előnye, hogy
hármasok halmazát, amelyek teljesítik (6)-ot. A (6) előnye, hogy ![]() szimmetriájú
szimmetriájú ![]() -ben, míg az (5)
-ben, míg az (5) ![]() szimmetriájú
szimmetriájú ![]() -ben.
-ben. ![]() esetén
esetén ![]() . Magasabb dimenzióban
. Magasabb dimenzióban
analóg (1)-gyel, a (2) analógja pedig
Ezen relációkra alapozva vezessük be az ![]() síkot. Ezt a síkot a
síkot. Ezt a síkot a ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() vektorok generálják, ezeket kardinális irányoknak nevezzük. Ezt a síkot ábrázolhatjuk úgy, hogy a felsorolt vektoroknak megfeleltetjük
vektorok generálják, ezeket kardinális irányoknak nevezzük. Ezt a síkot ábrázolhatjuk úgy, hogy a felsorolt vektoroknak megfeleltetjük ![]() -ben rendre az észak-nyugati, északi, észak-keleti, dél-keleti, déli, dél-nyugati irányokat úgy, hogy az észak-nyugati és észak-keleti irányok illetve a dél-keleti és dél-nyugati irányok
-ben rendre az észak-nyugati, északi, észak-keleti, dél-keleti, déli, dél-nyugati irányokat úgy, hogy az észak-nyugati és észak-keleti irányok illetve a dél-keleti és dél-nyugati irányok ![]() -os szöget zárnak be az északi illetve a déli iránnyal, nem pedig
-os szöget zárnak be az északi illetve a déli iránnyal, nem pedig ![]() -t. Diagramnak nevezünk olyan
-t. Diagramnak nevezünk olyan ![]() -beli intervallumokból (lehet egyik irányban végtelen intervallum) álló konfigurációt, amelynek minden éle párhuzamos a kardinális (észak-déli, északkelet-délnyugati, északnyugat-délkeleti) irányok egyikével és minden intervallum meg van számozva egy pozitív egész számmal, amelyet az intervallum multiplicitásának vagy tenziójának hívunk. Minden diagramhoz hozzárendelhetünk egy mértéket, amelyet úgy kapunk, hogy vesszük a Lebesgue-mértékek összegét minden intervallumon a multiplicitással súlyozva. Azt mondjuk, hogy a
-beli intervallumokból (lehet egyik irányban végtelen intervallum) álló konfigurációt, amelynek minden éle párhuzamos a kardinális (észak-déli, északkelet-délnyugati, északnyugat-délkeleti) irányok egyikével és minden intervallum meg van számozva egy pozitív egész számmal, amelyet az intervallum multiplicitásának vagy tenziójának hívunk. Minden diagramhoz hozzárendelhetünk egy mértéket, amelyet úgy kapunk, hogy vesszük a Lebesgue-mértékek összegét minden intervallumon a multiplicitással súlyozva. Azt mondjuk, hogy a ![]() és
és ![]() diagramok ekvivalensek ha a hozzájuk tartozó mértékek egyenlők.
diagramok ekvivalensek ha a hozzájuk tartozó mértékek egyenlők.
Ha ![]() egy diagram és
egy diagram és ![]() egy
egy ![]() -beli pont, akkor azt mondjuk, hogy
-beli pont, akkor azt mondjuk, hogy ![]() egy zéró-tenziójú pontja
egy zéró-tenziójú pontja ![]() -nak, ha
-nak, ha ![]() -nak egy elég kis környezetében,
-nak egy elég kis környezetében, ![]() ekvivalens
ekvivalens ![]() -ból kiinduló sugarak egy uniójával, amelyek koordináta vektorainak az összege megszorozva a multiplicitásukkal, 0-val egyenlő. Mivel a
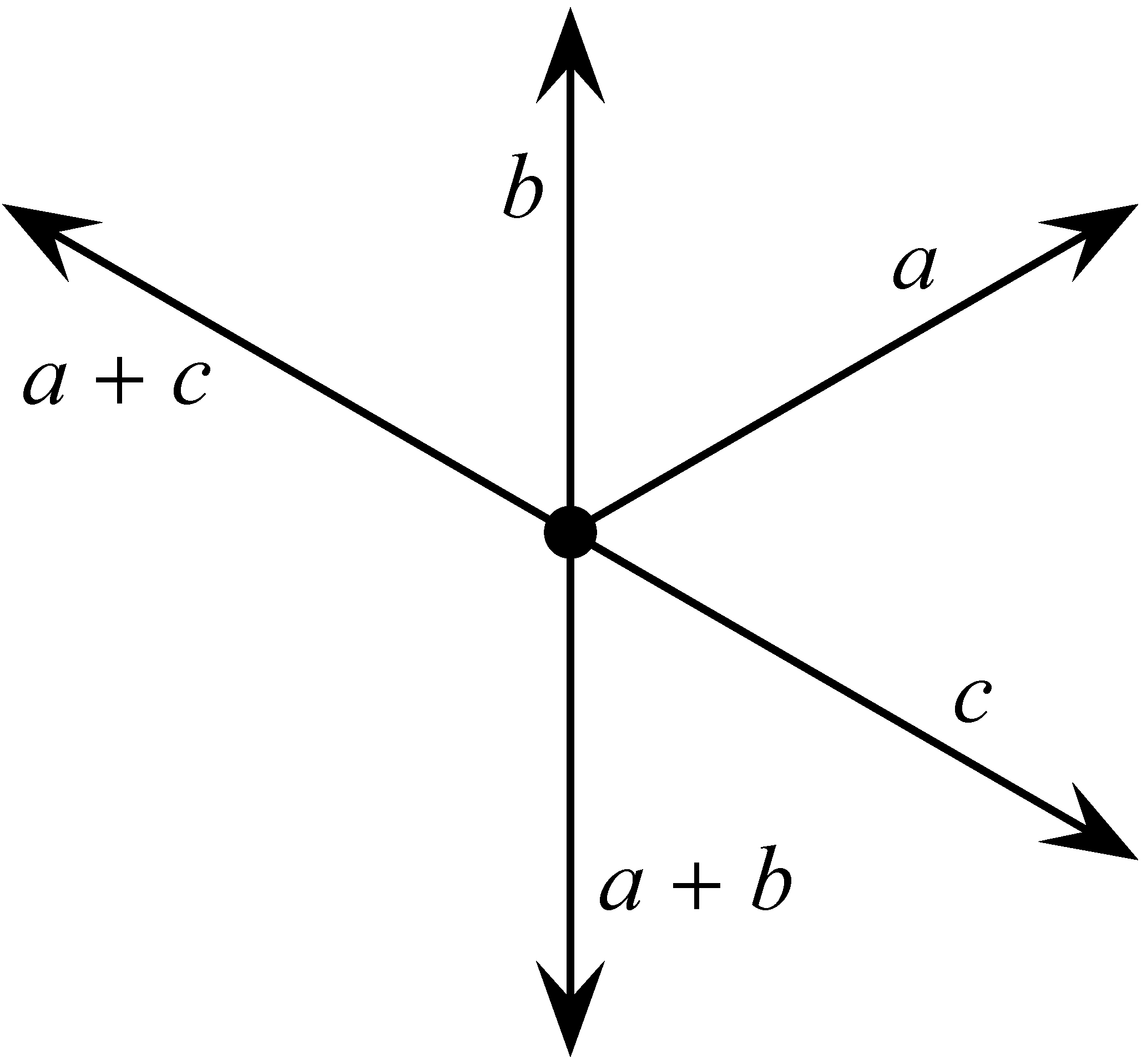
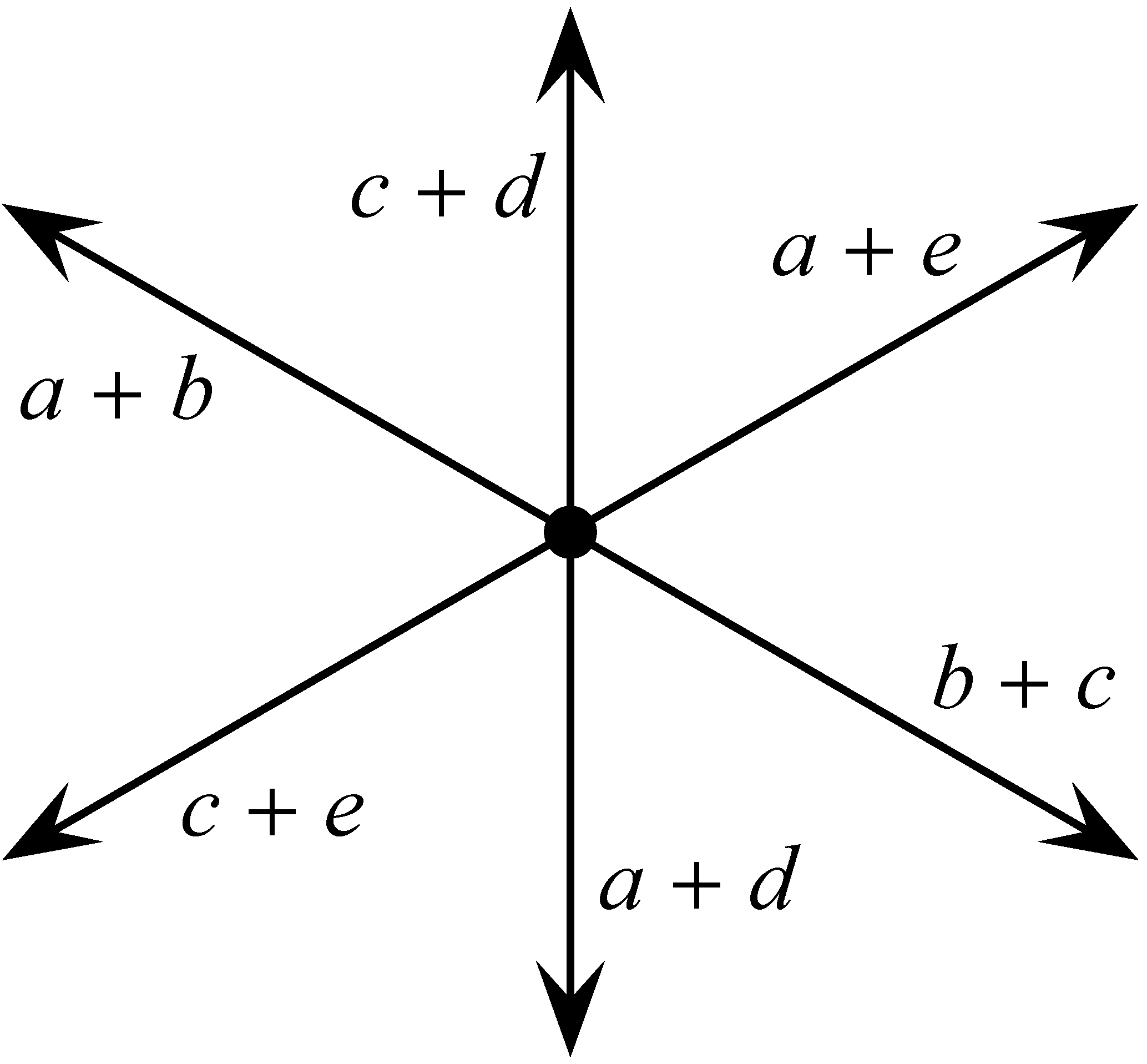
-ból kiinduló sugarak egy uniójával, amelyek koordináta vektorainak az összege megszorozva a multiplicitásukkal, 0-val egyenlő. Mivel a ![]() -ból kiinduló egység hosszúságú vektorok összegének, súlyozva a multiplicitásukkal, zérónak kell lennie, ha egy irány és ennek negatívja pozitív multiplicitással fordul elő, akkor kivonhatjuk őket egymásból. Két eset érdekel minket: 1) ha egy pont egy intervallumra esik, ebben az esetben a zéró-tenzió feltétel azt jelenti, hogy a pontból induló két sugárnak ugyanaz a multiplicitása; 2) ha egy pont egy
-ból kiinduló egység hosszúságú vektorok összegének, súlyozva a multiplicitásukkal, zérónak kell lennie, ha egy irány és ennek negatívja pozitív multiplicitással fordul elő, akkor kivonhatjuk őket egymásból. Két eset érdekel minket: 1) ha egy pont egy intervallumra esik, ebben az esetben a zéró-tenzió feltétel azt jelenti, hogy a pontból induló két sugárnak ugyanaz a multiplicitása; 2) ha egy pont egy ![]() alakú rész centruma, ebben az esetben a pontból induló három sugár ismét egyenlő multiplicitású. Ez és pár további eset látható az ábrákon, ahol az ábécé kis betűi a multiplicitást jelölik.
alakú rész centruma, ebben az esetben a pontból induló három sugár ismét egyenlő multiplicitású. Ez és pár további eset látható az ábrákon, ahol az ábécé kis betűi a multiplicitást jelölik.
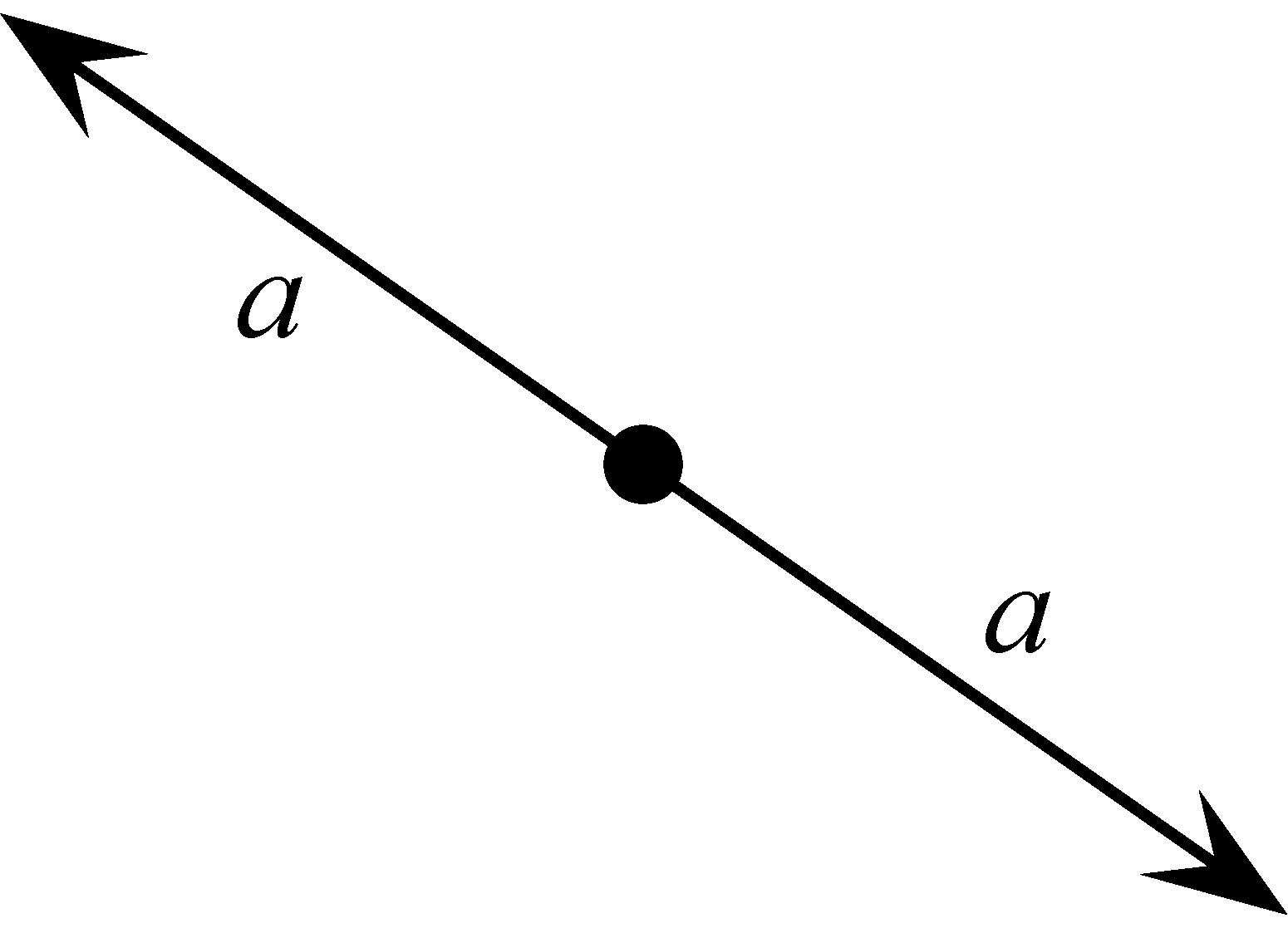
1. ábra: 1) eset
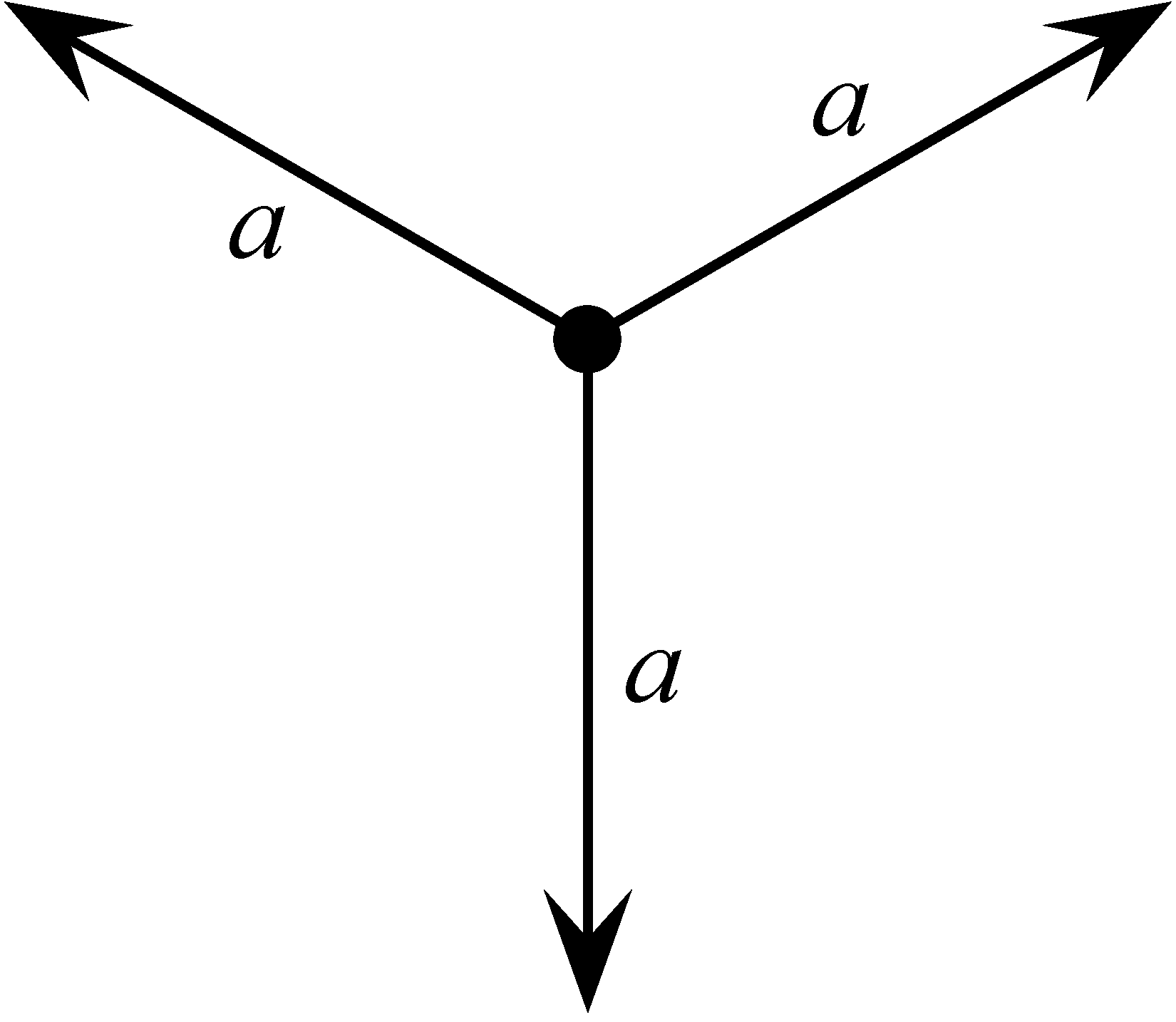
2. ábra: 2) eset
3. ábra
4. ábra
5. ábra
6. ábra
Egy méhkaptár egy olyan diagram (pontosabban diagramok ekvivalencia osztálya), hogy
1.) minden ![]() -beli pont zéró-tenziójú,
-beli pont zéró-tenziójú,
2.) csak véges sok olyan pont létezik, amelyből több, mint két sugár indul ki, ezeket csúcsoknak fogjuk hívni, (ezek csak a 2., 3., 4., 5., 6. ábrákon levő pontok lehetnek, itt a pontból kiinduló sugarak a multiplicitásukkal vannak számozva)
3.) a félig végtelen intervallumok csak észak-keleti, észak-nyugati és déli irányokba futnak. Ezeket az intervallumokat a méhkaptár határéleinek nevezzük.
Minden méhkaptár esetén mindhárom kardinális irányba ugyanannyi számú határél mutat az éleket a multiplicitásukkal együtt számolva, mivel a méhkaptár hálózat tenziója 0. ![]() -méhkaptárnak nevezzük a mindhárom irányban
-méhkaptárnak nevezzük a mindhárom irányban ![]() határéllel rendelkező méhkaptárt.
határéllel rendelkező méhkaptárt.
A 7. és a 8. ábrák két méhkaptárt mutatnak. Az 7. ábrán egy 4-méhkaptárat látunk, amelynek minden éle 1 multiplicitású, és csak olyan csúcspontjai vannak, ahol a pont egy ![]() alakzat centruma (lásd a 2. ábrát). A 8. ábrán egyetlen él van, amely 2 multiplicitású, ez déli irányú határél, a többi él multiplicitása 1. Van egy 1 multiplicitású déli irányú határél is, ezért a déli irányba 3 határél mutat, az észak-nyugati irányba és az észak-keleti irányba három-három 1 multiplicitású határél mutat. Ezért ez egy 3-méhkaptár.
alakzat centruma (lásd a 2. ábrát). A 8. ábrán egyetlen él van, amely 2 multiplicitású, ez déli irányú határél, a többi él multiplicitása 1. Van egy 1 multiplicitású déli irányú határél is, ezért a déli irányba 3 határél mutat, az észak-nyugati irányba és az észak-keleti irányba három-három 1 multiplicitású határél mutat. Ezért ez egy 3-méhkaptár.
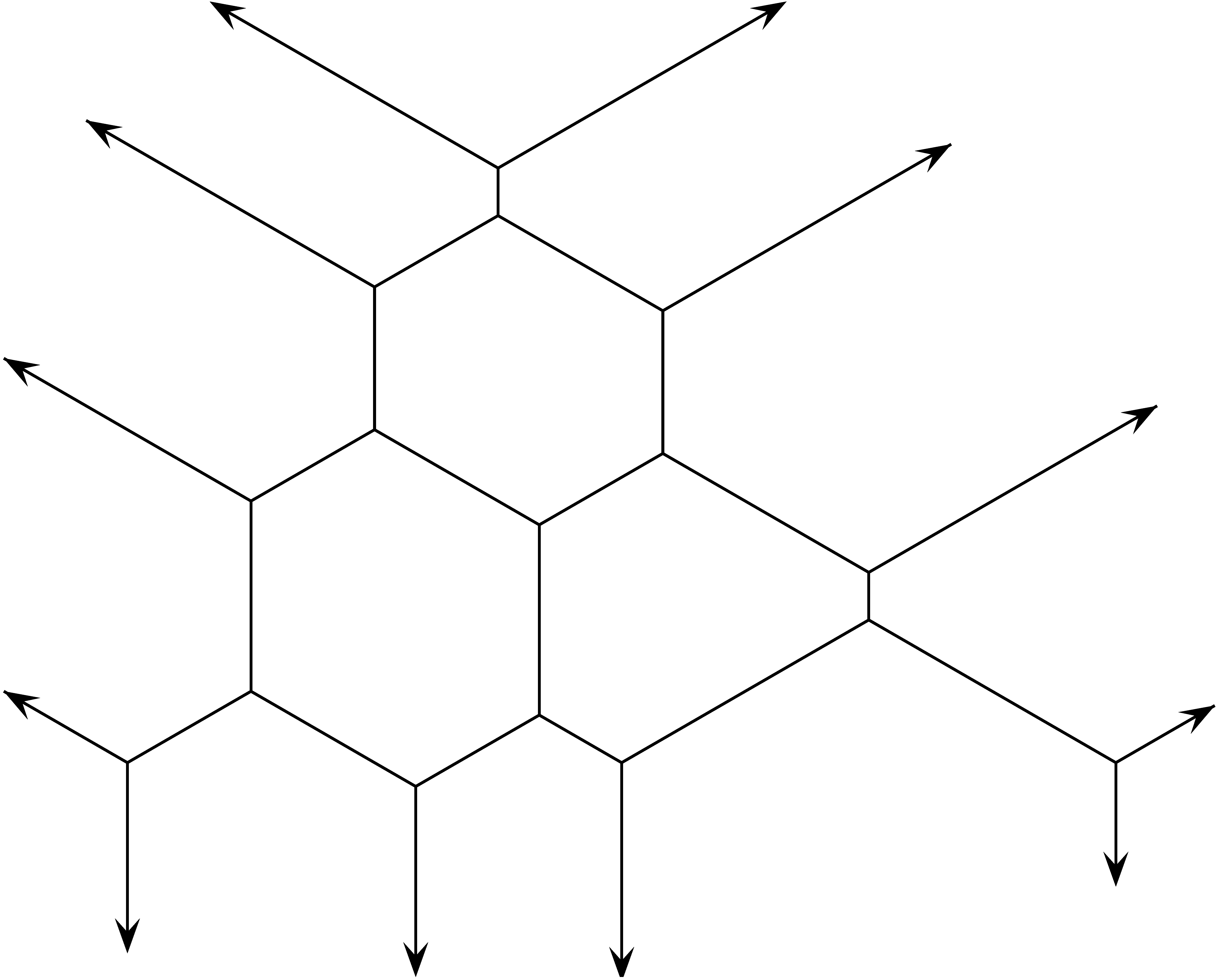
7. ábra
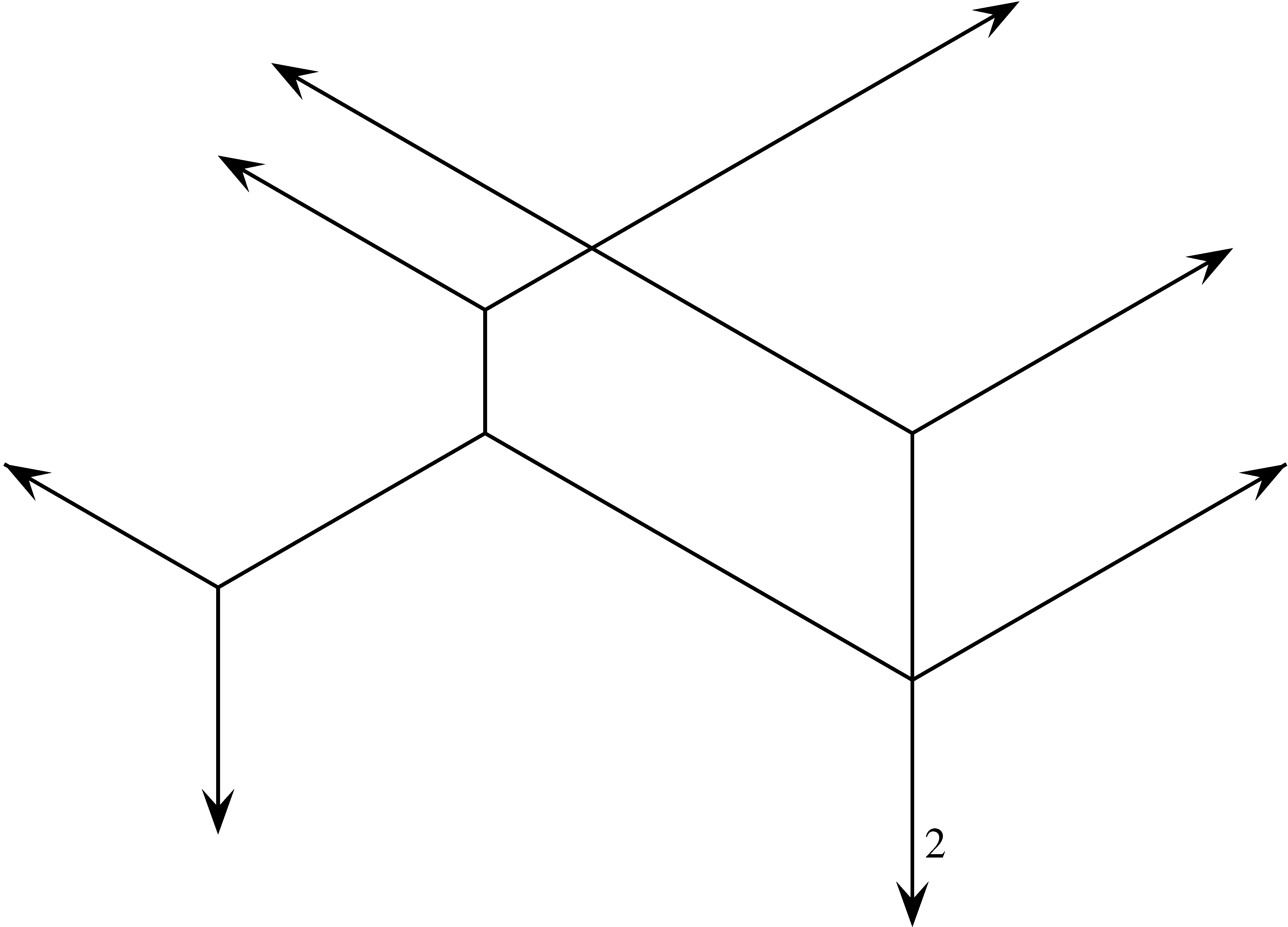
8. ábra
Mivel egy méhkaptárban minden él párhuzamos a kardinális irányok egyikével, és ezen irányok három koordinátájának egyike 0-val egyenlő, minden méhkaptárélnek van egy konstans koordinátája (ez a koordinátája közös az él menti összes pontnak). Vegyük a határélek konstans koordinátáit és írjuk, hogy
mint a 9. ábrán, ahol a görög betűk jelölik a konstans koordinátákat.

9. ábra
A következő tétel átfogalmazza a hermitikus mátrixok és az összegmátrixuk sajátértékei közötti problémát a síkbeli méhkaptár ábrázolásra:
1. tétel: Legyen ![]() ,
, ![]() ,
, ![]() valós számok monoton csökkenő
valós számok monoton csökkenő ![]() -esei. Akkor és csak akkor léteznek
-esei. Akkor és csak akkor léteznek ![]() ,
, ![]() és
és ![]() hermitikus mátrixok
hermitikus mátrixok ![]() ,
, ![]() ,
, ![]() sajátértékekkel, ha létezik egy méhkaptár, amely határéleinek konstans koordinátái
sajátértékekkel, ha létezik egy méhkaptár, amely határéleinek konstans koordinátái ![]() .
.
Az 1. tétel bizonyítása A. Knutson és T. Tao [4] cikkéből következik. Ennek a tételnek az átfogalmazása a (6) szimmetrizált relációra vonatkozóan:
2. tétel: A (6) reláció akkor és csak akkor teljesül, ha létezik egy méhkaptár ![]() konstans határél-koordinátákkal.
konstans határél-koordinátákkal.
Hogy érzékeltessük az 1. (vagy 2.) tétel igazságát, megadjuk az 1- és a 2-méhkaptárt: Ha ![]() , akkor
, akkor ![]() ,
, ![]() ,
, ![]() . A (6) reláció akkor és csak akkor teljesül, ha
. A (6) reláció akkor és csak akkor teljesül, ha ![]() . 1-méhkaptárat akkor és csak akkor kapunk, ha a három határél koordinátáinak összege 0. Az élek a konstans koordinátájukkal vannak számozva. Ezért az 1-méhkaptár
. 1-méhkaptárat akkor és csak akkor kapunk, ha a három határél koordinátáinak összege 0. Az élek a konstans koordinátájukkal vannak számozva. Ezért az 1-méhkaptár ![]() alakú (lásd a 10. bal oldali ábrát).
alakú (lásd a 10. bal oldali ábrát).
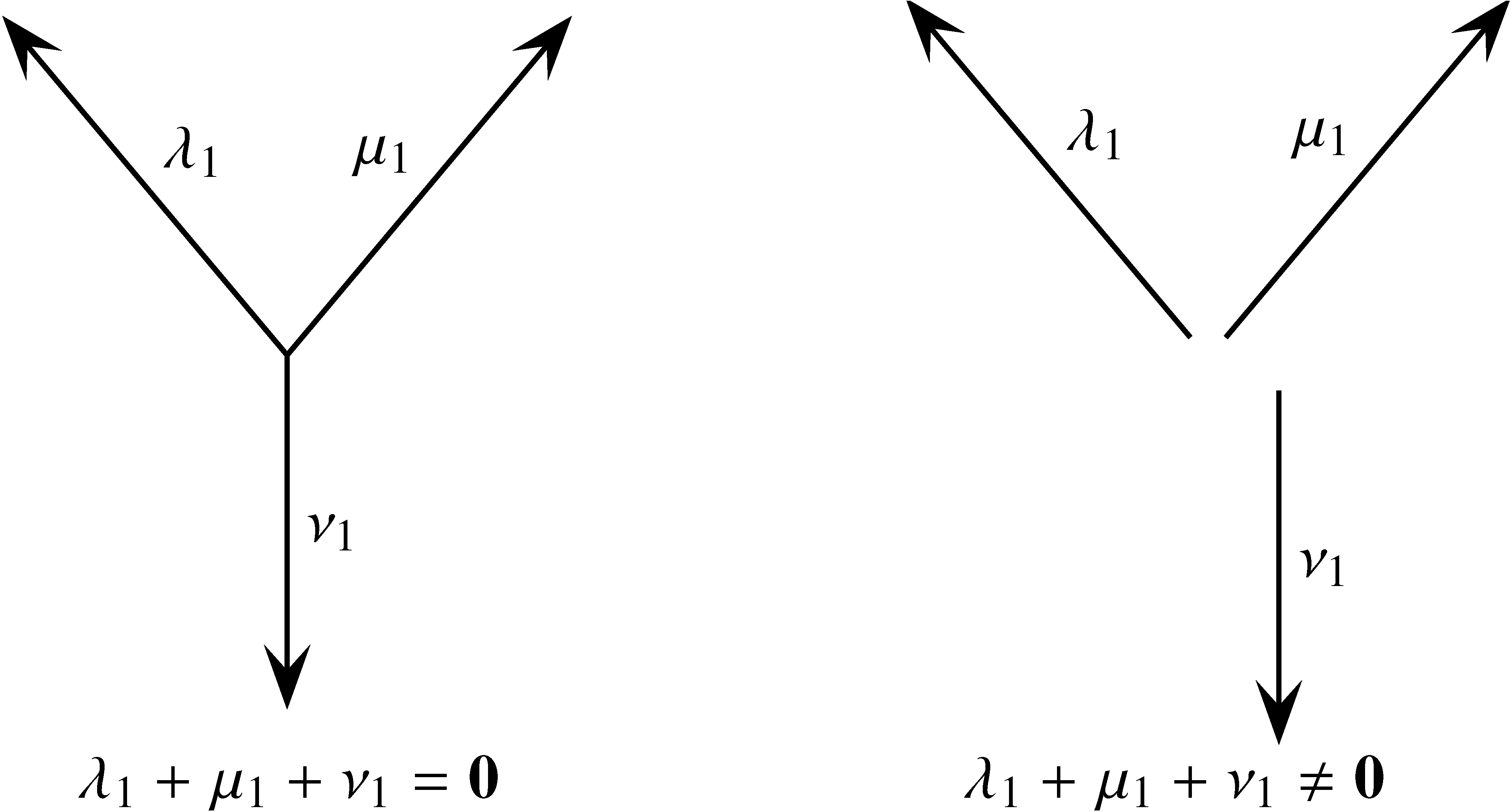
10. ábra
Most tekintsük az ![]() esetet. Ekkor
esetet. Ekkor ![]() ,
, ![]() ,
, ![]() . A 2-méhkaptár (lásd a 11. ábrát) egyértelműen meg van határozva a határél-koordinátákkal. Ezeknek teljesíteniük kell a nyomfeltételt, (1)-et. Továbbá az élek hosszúsága nem lehet negatív. Az éleket a konstans koordinátájukkal számozzuk. Az élek hosszát kiszámolhatjuk (egy irreleváns
. A 2-méhkaptár (lásd a 11. ábrát) egyértelműen meg van határozva a határél-koordinátákkal. Ezeknek teljesíteniük kell a nyomfeltételt, (1)-et. Továbbá az élek hosszúsága nem lehet negatív. Az éleket a konstans koordinátájukkal számozzuk. Az élek hosszát kiszámolhatjuk (egy irreleváns ![]() faktor erejéig) úgy, hogy kivonjuk két párhuzamos szomszédos él konstans koordinátáit. Például a
faktor erejéig) úgy, hogy kivonjuk két párhuzamos szomszédos él konstans koordinátáit. Például a ![]() -vel,
-vel, ![]() -vel,
-vel, ![]() -vel számozott élek hossza:
-vel számozott élek hossza: ![]() ,
, ![]() ,
, ![]() . Mivel ezek nem negatívak, megkapjuk a (3) szükséges feltételek analógjait, hogy
. Mivel ezek nem negatívak, megkapjuk a (3) szükséges feltételek analógjait, hogy ![]() ,
, ![]() ,
, ![]() .
. ![]() esetén ezek szükséges és elégséges feltételét adják a (6) reláció teljesülésének.
esetén ezek szükséges és elégséges feltételét adják a (6) reláció teljesülésének.
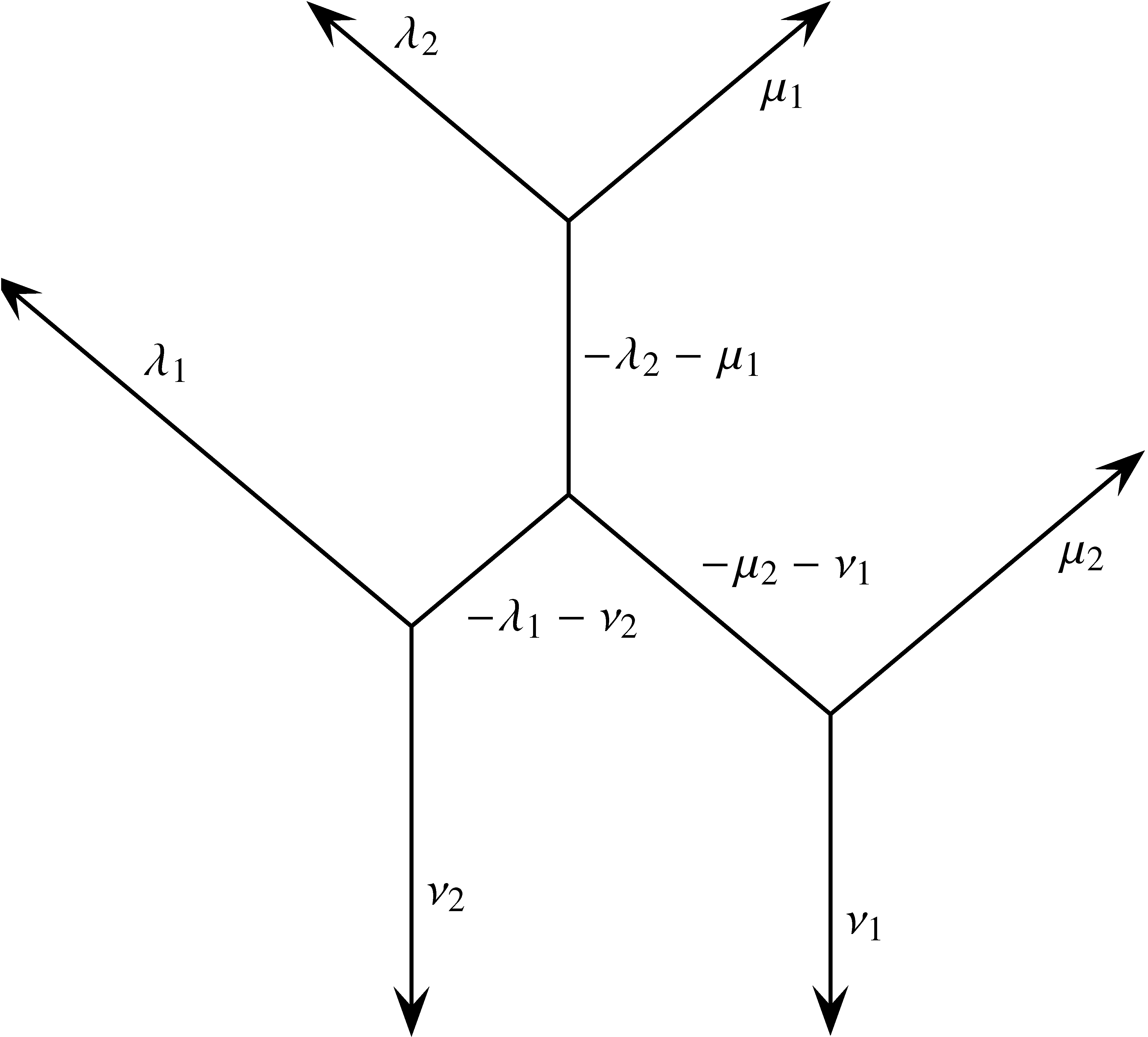
11. ábra
Magasabb dimenzióban több méhkaptár is létezik ugyanolyan határél-koordinátákkal. Az 1. tétel bizonyításához szükség van a tétel egy kvantált verziójára és annak bizonyítására. Először az (5) reláció kvantum verzióját adjuk meg. Ebben a relációban a ![]() ,
, ![]() ,
, ![]()
![]() -esekben csak egész számok fordulnak elő, míg az (5) relációban valós
-esekben csak egész számok fordulnak elő, míg az (5) relációban valós ![]()
![]() -esek vannak. A kvantált relációt egy kombinatorikai feladattal, a Littlewood-Richardson ferde táblázat létezésével vezetjük be. Ez a táblázat a
-esek vannak. A kvantált relációt egy kombinatorikai feladattal, a Littlewood-Richardson ferde táblázat létezésével vezetjük be. Ez a táblázat a ![]() csoport reprezentáció-elméletében kap fontos szerepet, amelyet az Appendixben írunk le. A Littlewood-Richardson ferde táblázat fogalmához a Young-diagram és -táblázat fogalmán keresztül jutunk.
csoport reprezentáció-elméletében kap fontos szerepet, amelyet az Appendixben írunk le. A Littlewood-Richardson ferde táblázat fogalmához a Young-diagram és -táblázat fogalmán keresztül jutunk.
Legyen ![]() egy pozitív egész szám.
egy pozitív egész szám. ![]() minden
minden ![]() ,
, ![]() , nemnegatív monoton csökkenő egész számok összegére történő felbontásához hozzárendeljük azt a diagramot, amely
, nemnegatív monoton csökkenő egész számok összegére történő felbontásához hozzárendeljük azt a diagramot, amely ![]() cellából áll, amelyek balra záródó sorokba rendeződnek úgy, hogy az első sorban
cellából áll, amelyek balra záródó sorokba rendeződnek úgy, hogy az első sorban ![]() , a második sorban
, a második sorban ![]() , ...,
, ..., ![]() .-sorban
.-sorban ![]() cella van. Ezt a diagramot Young-diagramnak hívjuk.
cella van. Ezt a diagramot Young-diagramnak hívjuk. ![]() felbontását pedig
felbontását pedig ![]() -nel fogjuk jelölni. A felbontáshoz tartozó cellákat pozitív egész számokkal töltjük ki úgy, hogy
-nel fogjuk jelölni. A felbontáshoz tartozó cellákat pozitív egész számokkal töltjük ki úgy, hogy
![]() a számok minden sorban balról jobbra monoton növekedően helyezkednek el és minden oszlopban fentről lefelé szigorúan monoton növekedően állnak. Ekkor Young-táblázatról beszélünk.
a számok minden sorban balról jobbra monoton növekedően helyezkednek el és minden oszlopban fentről lefelé szigorúan monoton növekedően állnak. Ekkor Young-táblázatról beszélünk.
A sztenderd Young-táblázat egy olyan táblázat, amelynek celláiba 1-től ![]() -ig írjuk be a számokat, mindegyiket egyszer. Általában egy táblázatban a számok többször is ismétlődhetnek. Például: A 12. ábra
-ig írjuk be a számokat, mindegyiket egyszer. Általában egy táblázatban a számok többször is ismétlődhetnek. Például: A 12. ábra ![]() Young-táblázatokat mutat, és a jobb oldali táblázat sztenderd.
Young-táblázatokat mutat, és a jobb oldali táblázat sztenderd.
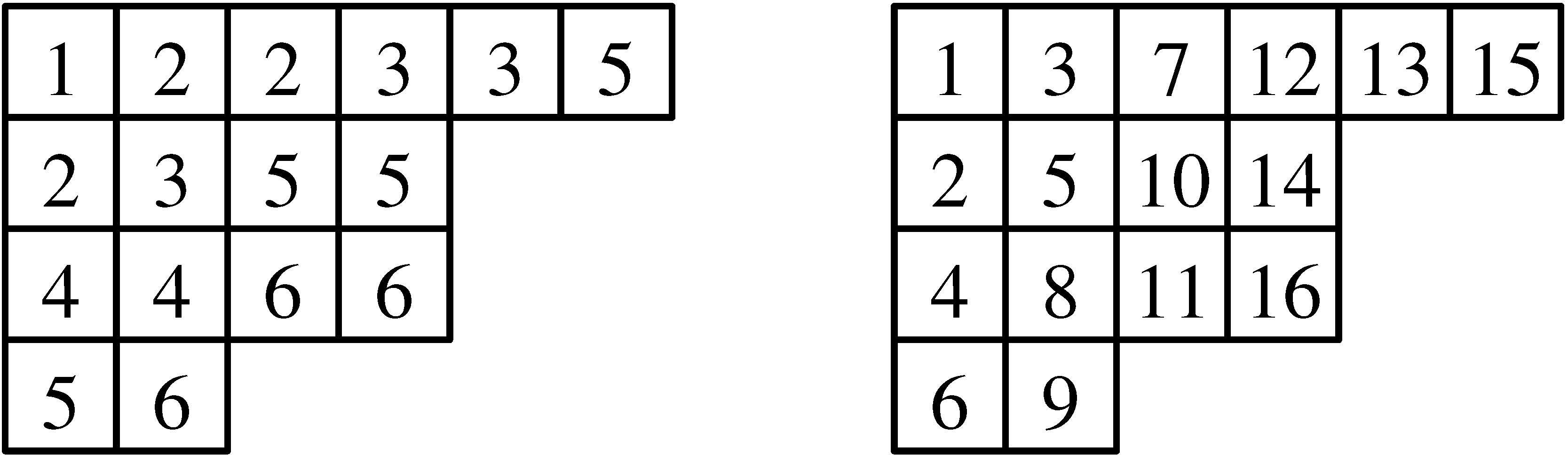
12. ábra
Ha két diagram az ![]() és a
és a ![]() felbontásokhoz tartozik úgy, hogy
felbontásokhoz tartozik úgy, hogy ![]() minden
minden ![]() -re, akkor azt mondjuk, hogy a
-re, akkor azt mondjuk, hogy a ![]() Young-diagramját tartalmazza az
Young-diagramját tartalmazza az ![]() Young-diagramja, és úgy jelöljük, hogy
Young-diagramja, és úgy jelöljük, hogy ![]() . Ferde diagramot,
. Ferde diagramot, ![]() -t akkor kapunk, ha egy nagyobb diagramból
-t akkor kapunk, ha egy nagyobb diagramból ![]() -ból kitöröljük egy kisebb diagram
-ból kitöröljük egy kisebb diagram ![]() celláit. Ferde táblázatról akkor beszélünk, ha egy ferde diagramot úgy töltünk ki pozitív egész számokkal, hogy teljesüljön a
celláit. Ferde táblázatról akkor beszélünk, ha egy ferde diagramot úgy töltünk ki pozitív egész számokkal, hogy teljesüljön a ![]() feltétel. Például: Ha
feltétel. Például: Ha ![]() és
és ![]() , akkor a 13. ábra bal oldala egy ferde diagramot, a jobb oldala egy ferde táblázatot mutat.
, akkor a 13. ábra bal oldala egy ferde diagramot, a jobb oldala egy ferde táblázatot mutat.
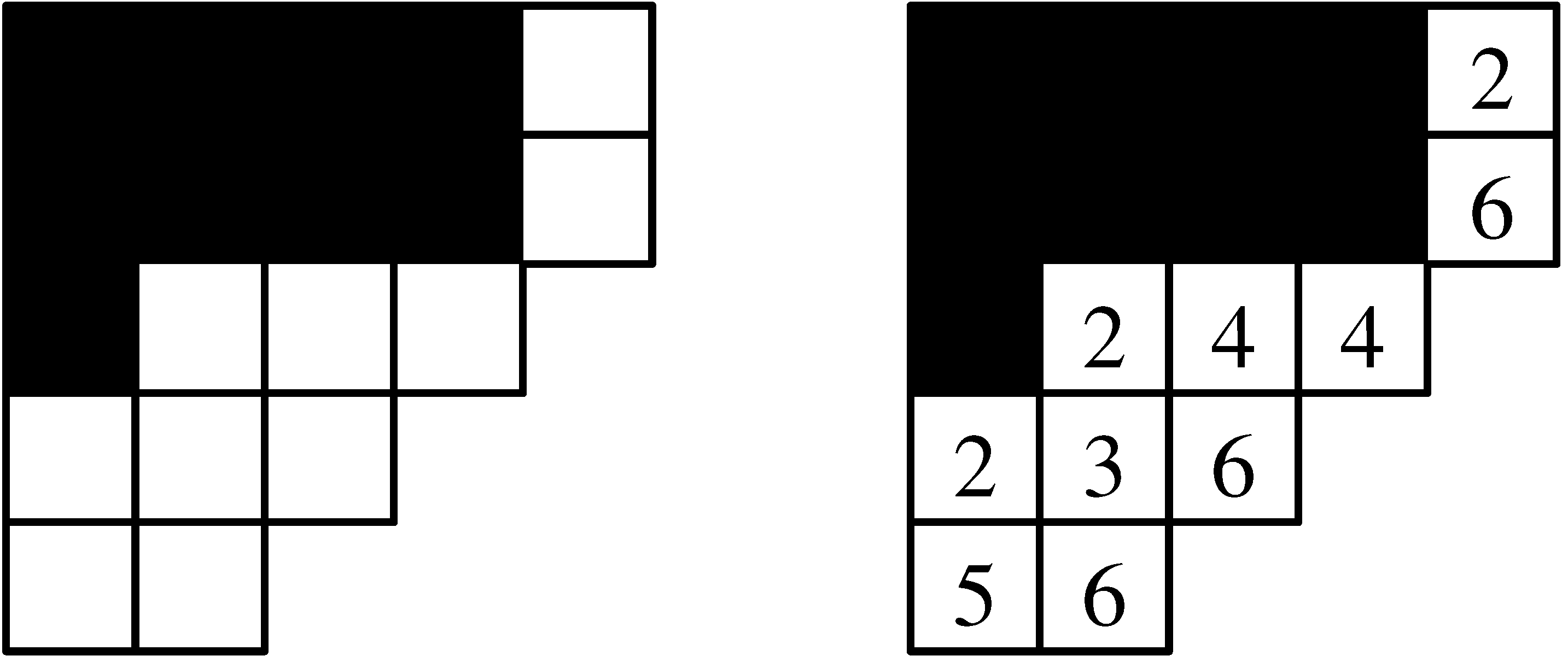
13. ábra
Az ![]() diagram celláit úgy rendezzük, hogy először felsoroljuk a legfelső sorban a cellákat jobbról balra, utána a második sorban a cellákat jobbról balra és így tovább. A
diagram celláit úgy rendezzük, hogy először felsoroljuk a legfelső sorban a cellákat jobbról balra, utána a második sorban a cellákat jobbról balra és így tovább. A ![]() alakú ferde diagram
alakú ferde diagram ![]() tartalmú, ha a diagramot
tartalmú, ha a diagramot ![]() 1-gyel,
1-gyel, ![]() 2-vel,
2-vel, ![]()
![]() -nel töltjük ki úgy, hogy teljesüljön a következő tulajdonság: Minden
-nel töltjük ki úgy, hogy teljesüljön a következő tulajdonság: Minden ![]() -re,
-re, ![]() , és minden
, és minden ![]() -re,
-re, ![]() , az a szám, ahányszor
, az a szám, ahányszor ![]() előfordul a rendezés szerinti első
előfordul a rendezés szerinti első ![]() cellában, legalább akkora, mint ahányszor az
cellában, legalább akkora, mint ahányszor az ![]() előfordul ebben az első
előfordul ebben az első ![]() cellában. Az így kitöltött táblázatot nevezzük Littlewood-Richardson ferde táblázatnak
cellában. Az így kitöltött táblázatot nevezzük Littlewood-Richardson ferde táblázatnak ![]() alakkal és
alakkal és ![]() tartalommal. Például: Ha
tartalommal. Például: Ha ![]() ,
, ![]() , és
, és ![]() rendre
rendre ![]() ,
, ![]() ,
, ![]() akkor a 14. ábrán látható Littlewood-Richardson ferde táblázatokat kapjuk:
akkor a 14. ábrán látható Littlewood-Richardson ferde táblázatokat kapjuk:
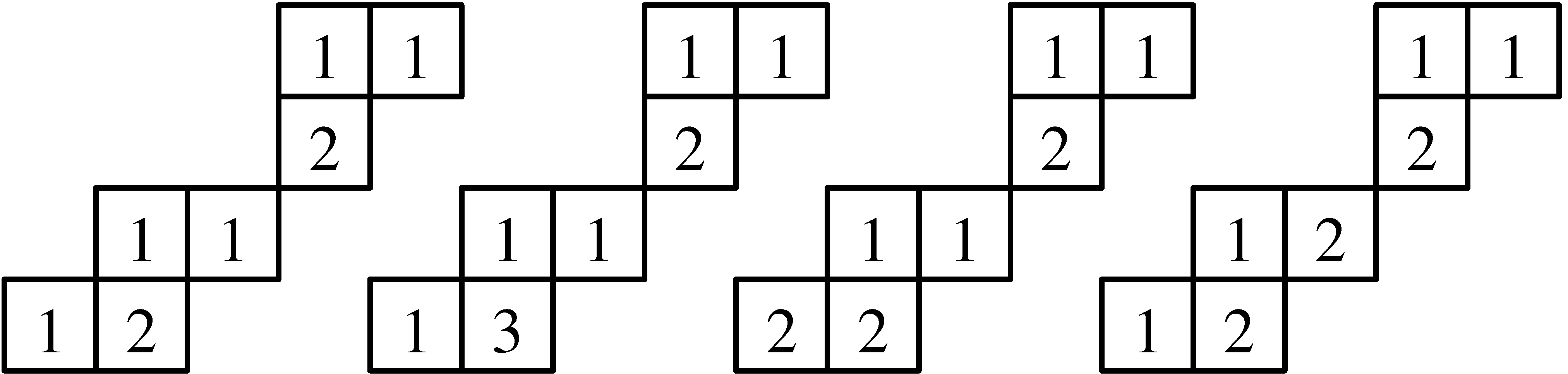
14. ábra
Az (5) reláció kvantum analógja
akkor áll fenn, ha létezik legalább egy Littlewood-Richardson ferde táblázat ![]() alakkal és
alakkal és ![]() tartalommal.
tartalommal.
Látható, hogy a ![]() feltétel, amely az (1) nyomfeltétel, szükséges ahhoz, hogy létezzen Littlewood-Richardson ferde táblázat
feltétel, amely az (1) nyomfeltétel, szükséges ahhoz, hogy létezzen Littlewood-Richardson ferde táblázat ![]() alakkal és
alakkal és ![]() tartalommal. A kapcsolat a klasszikus és a kvantum reláció között a következő:
tartalommal. A kapcsolat a klasszikus és a kvantum reláció között a következő:
3. tétel: Legyenek ![]() ,
, ![]() ,
, ![]() egész számok monoton csökkenő
egész számok monoton csökkenő ![]() -esei.
-esei.
1. Ha (7) teljesül, akkor teljesül (5).
2. Fordítva, ha (5) teljesül, akkor létezik egy ![]() egész szám úgy, hogy
egész szám úgy, hogy ![]() , ahol
, ahol ![]() .
.
Továbbá teljesül a következő állítás:
4. állítás: A fenti tételben ![]() -nek vehető, azaz (5) és (7) ekvivalens egész
-nek vehető, azaz (5) és (7) ekvivalens egész ![]() ,
, ![]() ,
, ![]()
![]() -esekre.
-esekre.
A 4. állítás saturation-sejtésként volt ismert, és az első bizonyítását A. Knutson és T. Tao adták [4]-ben.
Az 1. tétel kvantum analógjának megfogalmazásához megadjuk az egész méhkaptár definicióját.
Egy méhkaptárt egész méhkaptárnak nevezzük, ha csúcspontjai (amelyekből legalább két él indul ki) egész koordinátájúak, azaz ![]() -beliek.
-beliek.
Egy egész méhkaptár határél-koordinátái szükségszerűen egészek.
5. tétel: A (7) reláció pontosan akkor teljesül, ha létezik egy egész méhkaptár ![]() határél-koordinátákkal.
határél-koordinátákkal.
A 5. és a 3. tételekből következik az 1. és a 2. tétel. A. Knutson és T. Tao leredukálták [4]-ben a saturation-sejtést a következő méhkaptárral kapcsolatos problémára, amelyet [4]-ben be is bizonyítottak.
6. tétel: Legyen ![]() egy valós értékű méhkaptár egész határél-koordinátákkal. Ekkor létezik egy
egy valós értékű méhkaptár egész határél-koordinátákkal. Ekkor létezik egy ![]() egész méhkaptár ugyanazokkal a határél-koordinátákkal, mint
egész méhkaptár ugyanazokkal a határél-koordinátákkal, mint ![]() .
.
Ezzel megadták a saturation-sejtés első bizonyítását. Most újra fogalmazzuk a Horn sejtést, felhasználva A. A. Klyachko eredményét (lásd. [3]). Horn bebizonyította [2]-ben, hogy az (5) reláció megoldáshalmaza megadható az (1) által, és véges számú
alakú egyenlőtlenség által, ahol ![]() , és
, és ![]() ,
, ![]() ,
, ![]() egész számok monoton csökkenő sorozatai 0 és
egész számok monoton csökkenő sorozatai 0 és ![]() között inkluzívan. Egy ilyen formájú
között inkluzívan. Egy ilyen formájú ![]() hármast megengedettnek nevezünk. Például (2) a
hármast megengedettnek nevezünk. Például (2) a ![]() megengedett hármassal (8) alakú. Indukcióval megmutatható, hogy a Horn-sejtés ekvivalens a következővel:
megengedett hármassal (8) alakú. Indukcióval megmutatható, hogy a Horn-sejtés ekvivalens a következővel:
7. sejtés: Legyenek ![]() ,
, ![]() ,
, ![]() valós számok monoton csökkenő sorozatai. Ekkor az (5) reláció akkor és csak akkor teljesül, ha (1) fennáll és (8) teljesül mindannyiszor, amikor
valós számok monoton csökkenő sorozatai. Ekkor az (5) reláció akkor és csak akkor teljesül, ha (1) fennáll és (8) teljesül mindannyiszor, amikor ![]() ,
, ![]() ,
, ![]() megengedett és
megengedett és ![]() .
.
A. A. Klyachko a [3]-ban megmutatta, hogy a Horn-sejtés igaz, ha a klasszikus ![]() relációt a kvantum
relációt a kvantum ![]() relációval helyettesítjük
relációval helyettesítjük ![]() -n:
-n:
8. tétel: Legyenek ![]() ,
, ![]() ,
, ![]() valós számok monoton csökkenő sorozatai, amelyek teljesítik (1)-et.
valós számok monoton csökkenő sorozatai, amelyek teljesítik (1)-et.
1. Ha (5) reláció teljesül, akkor (8) mindannyiszor teljesül, amikor ![]() ,
, ![]() ,
, ![]() megengedett és
megengedett és ![]() .
.
2. Fordítva, ha (8) teljesül mindannyiszor, amikor ![]() ,
, ![]() ,
, ![]() megengedett és
megengedett és ![]() , akkor teljesül az (5) reláció.
, akkor teljesül az (5) reláció.
Így az dimenziós kvantumprobléma megoldhatósága meghatározza a Weyl-feladat megoldhatóságát a klasszikus
![]() -dimenziós problémára ((
-dimenziós problémára (( ![]() )-es hermitikus mátrixok összegére). A saturation-tétel bizonyítása, amely azt mondja, hogy minden ilyen kvantumprobléma pontosan akkor megoldható, ha a hozzá tartozó klasszikus probléma (ugyanabban a dimenzióban) megoldható, rekurzív módot ad a Horn-sejtés bizonyítására.
)-es hermitikus mátrixok összegére). A saturation-tétel bizonyítása, amely azt mondja, hogy minden ilyen kvantumprobléma pontosan akkor megoldható, ha a hozzá tartozó klasszikus probléma (ugyanabban a dimenzióban) megoldható, rekurzív módot ad a Horn-sejtés bizonyítására.
A [6] cikkben A. Knutson, T. Tao és C. Woodward megadták a 8. tételnek egy tisztán méhkaptár-elméleti bizonyítását , ezzel a Horn-sejtésnek egy bizonyítását, direkt módon a saturation-sejtésből. Az [5] cikket szeretném ajánlani mindazoknak, akik szeretnének megismerkedni ezen gondolatkör bizonyításának az ötleteivel.
Appendix
A ![]() kvantumreláció az
kvantumreláció az ![]() unitér csoport irreducibilis reprezentációival vagy ami ezzel ekvivalens, a
unitér csoport irreducibilis reprezentációival vagy ami ezzel ekvivalens, a ![]() véges dimenziós irreducibilis holomorf reprezentációival áll szoros kapcsolatban. Minden ilyen reprezentációnak van egy legnagyobb súlya, amely egy monoton csökkenő
véges dimenziós irreducibilis holomorf reprezentációival áll szoros kapcsolatban. Minden ilyen reprezentációnak van egy legnagyobb súlya, amely egy monoton csökkenő ![]() egész számokból álló
egész számokból álló ![]() -es.
-es. ![]() irreducibilis polinomiális reprezentációi a következőképpen adhatók meg (lásd [1], Section 8, Representations of the general linear group): A konstrukcióhoz szükségünk lesz a korábban definiált Young -diagramra. A
irreducibilis polinomiális reprezentációi a következőképpen adhatók meg (lásd [1], Section 8, Representations of the general linear group): A konstrukcióhoz szükségünk lesz a korábban definiált Young -diagramra. A ![]() , ahol
, ahol ![]() egy
egy ![]() -dimenziós komplex vektortér, irreducibilis polinomiális reprezentációi a
-dimenziós komplex vektortér, irreducibilis polinomiális reprezentációi a ![]() maximálisan
maximálisan ![]() sorból álló Young-diagramjai által paraméterezhetők, és bázisaik a
sorból álló Young-diagramjai által paraméterezhetők, és bázisaik a ![]() Young-táblázataihoz rendelhetők, amelynek elemei
Young-táblázataihoz rendelhetők, amelynek elemei ![]() -beliek. Ha
-beliek. Ha ![]() , (azaz a
, (azaz a ![]() Young-diagramja egy sorban levő
Young-diagramja egy sorban levő ![]() cellából áll) akkor a
cellából áll) akkor a ![]() reprezentáció (Schur- vagy Weyl-modul) a
reprezentáció (Schur- vagy Weyl-modul) a ![]()
![]() -edik szimmetrikus hatványa
-edik szimmetrikus hatványa ![]() -nek. Ha
-nek. Ha ![]() , (azaz a
, (azaz a ![]() Young-diagramja egy oszlopban levő
Young-diagramja egy oszlopban levő ![]() cellából áll) akkor a
cellából áll) akkor a ![]() reprezentáció az
reprezentáció az ![]() -eddik
-eddik ![]() külső hatványtér.
külső hatványtér.
A további reprezentációk megkonstruálásához szükséges a kicserélés fogalma. Ez egy ![]() Young-diagram két oszlopának és a két oszlopban ugyanannyi számú cellának a kiválasztásától függ. A
Young-diagram két oszlopának és a két oszlopban ugyanannyi számú cellának a kiválasztásától függ. A ![]() diagram minden
diagram minden ![]() kitöltését megengedjük (tetszőlegesen rendezhetjük el a cellákban az elemeket). A
kitöltését megengedjük (tetszőlegesen rendezhetjük el a cellákban az elemeket). A ![]() kitöltött diagramból a kicserélés után úgy kapjuk
kitöltött diagramból a kicserélés után úgy kapjuk ![]() -et, hogy a kiválasztott két oszlopban felcseréljük a két kiválasztott cellahalmazban levő elemeket, megtartva mindkettő merőleges rendezését, és a többi elemet változatlanul hagyjuk. Például: Ha
-et, hogy a kiválasztott két oszlopban felcseréljük a két kiválasztott cellahalmazban levő elemeket, megtartva mindkettő merőleges rendezését, és a többi elemet változatlanul hagyjuk. Például: Ha ![]() és a harmadik oszlopból a felső két cellát, a második oszlopból a második és a negyedik cellát választjuk, akkor a kicserélés eredményéül a
és a harmadik oszlopból a felső két cellát, a második oszlopból a második és a negyedik cellát választjuk, akkor a kicserélés eredményéül a ![]() kitöltött diagramból az
kitöltött diagramból az ![]() -t kapjuk (lásd 15. ábrát).
-t kapjuk (lásd 15. ábrát).

15. ábra
Jelölje ![]() a
a ![]() vektortér
vektortér ![]() másolatának a Descartes-szorzatát, amely a
másolatának a Descartes-szorzatát, amely a ![]() Young-diagramjának
Young-diagramjának ![]() cellája szerint van számozva. Így egy
cellája szerint van számozva. Így egy ![]() elem megadható
elem megadható ![]() minden cellájára
minden cellájára ![]() egy speciális eleme által. Legyen
egy speciális eleme által. Legyen ![]() egy komplex vektortér. Tekintsük a
egy komplex vektortér. Tekintsük a ![]() leképezéseket, amelyek teljesítik a következő tulajdonságokat:
leképezéseket, amelyek teljesítik a következő tulajdonságokat:
(1) ![]()
![]() -multilineáris,
-multilineáris,
(2) ![]() alternáló
alternáló ![]() minden oszlopának elemeiben, azaz
minden oszlopának elemeiben, azaz ![]() eltűnik, ha két elem ugyanabban az oszlopban megegyezik. Az (1)-gyel együtt ebből az következik, hogy
eltűnik, ha két elem ugyanabban az oszlopban megegyezik. Az (1)-gyel együtt ebből az következik, hogy ![]() , ha
, ha ![]() -t úgy kapjuk
-t úgy kapjuk ![]() -ből, hogy felcserélünk két elemet egy oszlopban.
-ből, hogy felcserélünk két elemet egy oszlopban.
(3) Minden ![]() -ra
-ra ![]() , ahol az összegzés az összes olyan
, ahol az összegzés az összes olyan ![]() -re történik, amelyet
-re történik, amelyet ![]() -ből kapunk úgy, hogy két adott oszlop között kicseréljük a jobb oldali választott oszlop egy adott cellahalmazát. Például: Ha
-ből kapunk úgy, hogy két adott oszlop között kicseréljük a jobb oldali választott oszlop egy adott cellahalmazát. Például: Ha ![]() és a második oszlopban a felső cellát választjuk, akkor a 16. ábrán levő egyenletet kapjuk.
és a második oszlopban a felső cellát választjuk, akkor a 16. ábrán levő egyenletet kapjuk.
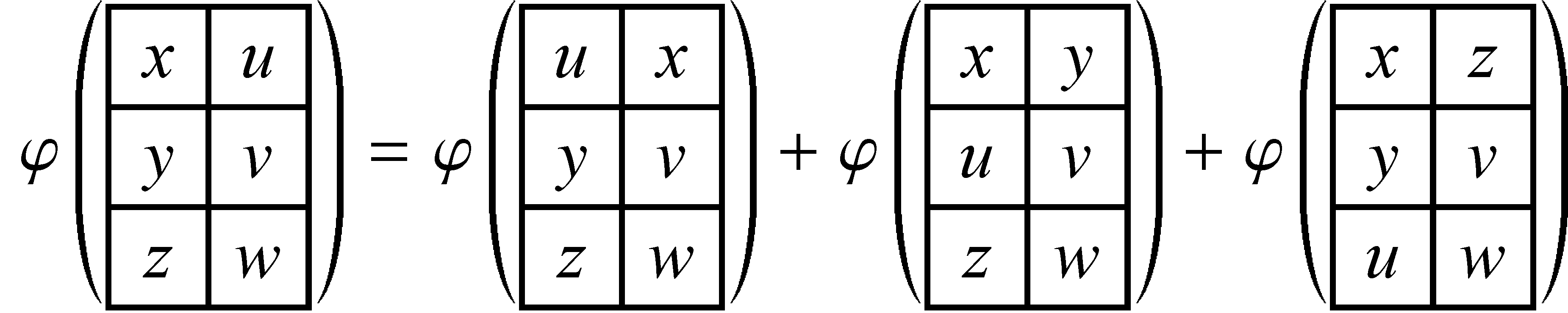
16. ábra
A ![]() Schur-modul egy
Schur-modul egy ![]() -vektortér úgy, hogy létezik egy
-vektortér úgy, hogy létezik egy ![]() leképezés, amely teljesíti (1)–(3)-t, és minden
leképezés, amely teljesíti (1)–(3)-t, és minden ![]() leképezésre, amely teljesíti (1)–(3)-t létezik egy egyértelmű
leképezésre, amely teljesíti (1)–(3)-t létezik egy egyértelmű ![]() homomorfizmus, amelyre
homomorfizmus, amelyre ![]() teljesül minden
teljesül minden ![]() esetén.
esetén. ![]() megkonstruálásához először vegyük észre, hogy az (1) tulajdonságú univerzális modul a
megkonstruálásához először vegyük észre, hogy az (1) tulajdonságú univerzális modul a ![]() tenzorszorzata
tenzorszorzata ![]()
![]() másolatának, ahol a faktorok
másolatának, ahol a faktorok ![]() cellái szerint vannak indexelve. Az (1) és (2) tulajdonságú univerzális modul a hányados modulja
cellái szerint vannak indexelve. Az (1) és (2) tulajdonságú univerzális modul a hányados modulja ![]() -nak azzal a részmodullal, amelyet
-nak azzal a részmodullal, amelyet ![]() elemeiből képzett olyan tenzorok generálnak, amelyeknek van két egyező eleme ugyanabban az oszlopban. Az ebben a lépésben kapott modul azonosítható a
elemeiből képzett olyan tenzorok generálnak, amelyeknek van két egyező eleme ugyanabban az oszlopban. Az ebben a lépésben kapott modul azonosítható a ![]() modullal, ahol
modullal, ahol ![]() a Young diagram
a Young diagram ![]() -dik oszlopának hossza, azaz
-dik oszlopának hossza, azaz ![]() . Például: a 17. ábra esetén
. Például: a 17. ábra esetén ![]() egy
egy ![]() diagram, a konjugáltja
diagram, a konjugáltja ![]() egy
egy ![]() diagram.
diagram.
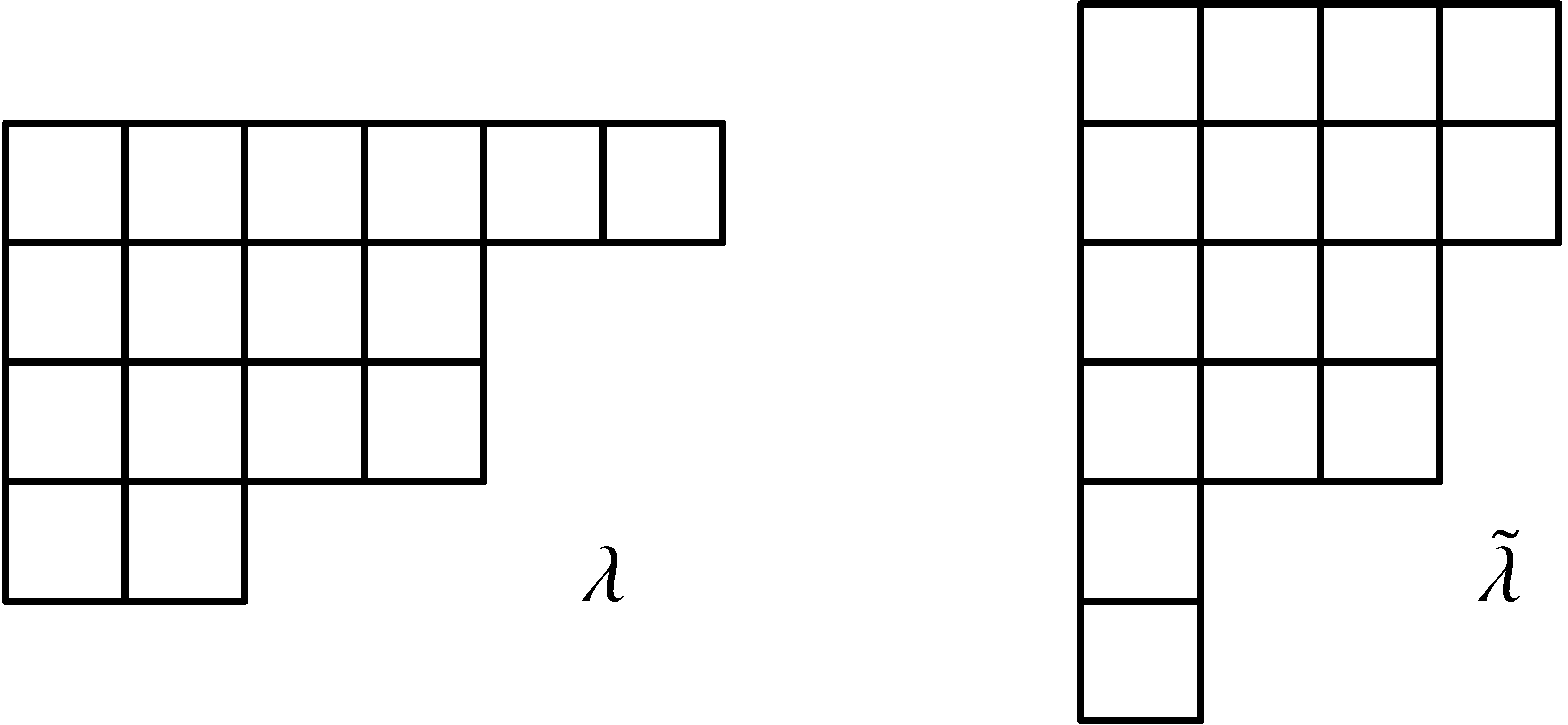
17. ábra
Ha adott egy vektor ![]() -ban, akkor tekintsük minden oszlopban az elemek külső szorzatát az oszlop tetejétől az aljáig, és vegyük ezeknek az osztályoknak a tenzorszorzatát (lásd a 18. ábrát)
-ban, akkor tekintsük minden oszlopban az elemek külső szorzatát az oszlop tetejétől az aljáig, és vegyük ezeknek az osztályoknak a tenzorszorzatát (lásd a 18. ábrát)
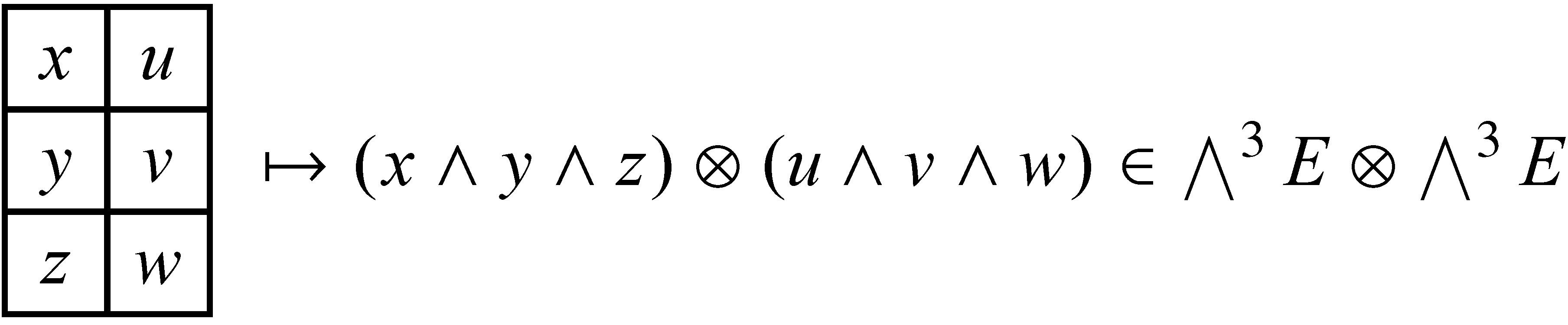
18. ábra
Jelöljük ezt a ![]() leképezést
leképezést ![]() -vel. Ekkor
-vel. Ekkor ![]() a
a ![]() hányadosmodul, ahol
hányadosmodul, ahol ![]() az a részmodul, amely az összes
az a részmodul, amely az összes ![]() alakú elem által van generálva, ahol az összegzés az összes olyan
alakú elem által van generálva, ahol az összegzés az összes olyan ![]() elemre megy, amelyet
elemre megy, amelyet ![]() -ből a (3)-ban leírt kicseréléssel kapunk. Például:
-ből a (3)-ban leírt kicseréléssel kapunk. Például: ![]() a hányadosa
a hányadosa ![]() -nek az összes
-nek az összes ![]() alakú vektorok által generált részmodullal.
alakú vektorok által generált részmodullal.
Tegyük fel, hogy van egy rendezett ![]() , ...,
, ..., ![]() halmaza
halmaza ![]() elemeinek. Ekkor minden
elemeinek. Ekkor minden ![]() kitöltésére a
kitöltésére a ![]() diagramnak
diagramnak ![]() elemeivel, megkapunk
elemeivel, megkapunk ![]() -nek egy elemét, ha helyettesítjük a
-nek egy elemét, ha helyettesítjük a ![]() celláiban minden
celláiban minden ![]() -t
-t ![]() -vel. Ennek az elemnek a képe
-vel. Ennek az elemnek a képe ![]() -ben legyen
-ben legyen ![]() . Legyen
. Legyen ![]() a diagonális mátrixok részcsoportja és jelöljük
a diagonális mátrixok részcsoportja és jelöljük ![]() -nel az
-nel az ![]() , ...,
, ..., ![]() elemű diagonális mátrixot
elemű diagonális mátrixot ![]() -ban. Egy
-ban. Egy ![]() vektort súlyvektornak nevezünk a
vektort súlyvektornak nevezünk a ![]() súllyal
súllyal ![]() , ha
, ha ![]() minden
minden ![]() esetén. Legyen
esetén. Legyen ![]() a felső trianguláris mátrixok Borel-részcsoportja. Egy
a felső trianguláris mátrixok Borel-részcsoportja. Egy ![]() súlyvektort legnagyobb súlyú vektornak nevezzük, ha
súlyvektort legnagyobb súlyú vektornak nevezzük, ha ![]() . Egy nemnulla skalárszorzás erejéig az egyetlen legnagyobb súlyú vektor a
. Egy nemnulla skalárszorzás erejéig az egyetlen legnagyobb súlyú vektor a ![]() reprezentációban az
reprezentációban az ![]() vektor, ahol
vektor, ahol ![]() a
a ![]() -nek az a táblázata, amelynek
-nek az a táblázata, amelynek ![]() -dik sora csak az
-dik sora csak az ![]() egész számot tartalmazza. Például:
egész számot tartalmazza. Például: ![]() esetén a 19. ábra mutatja a
esetén a 19. ábra mutatja a ![]() táblázatot.
táblázatot.
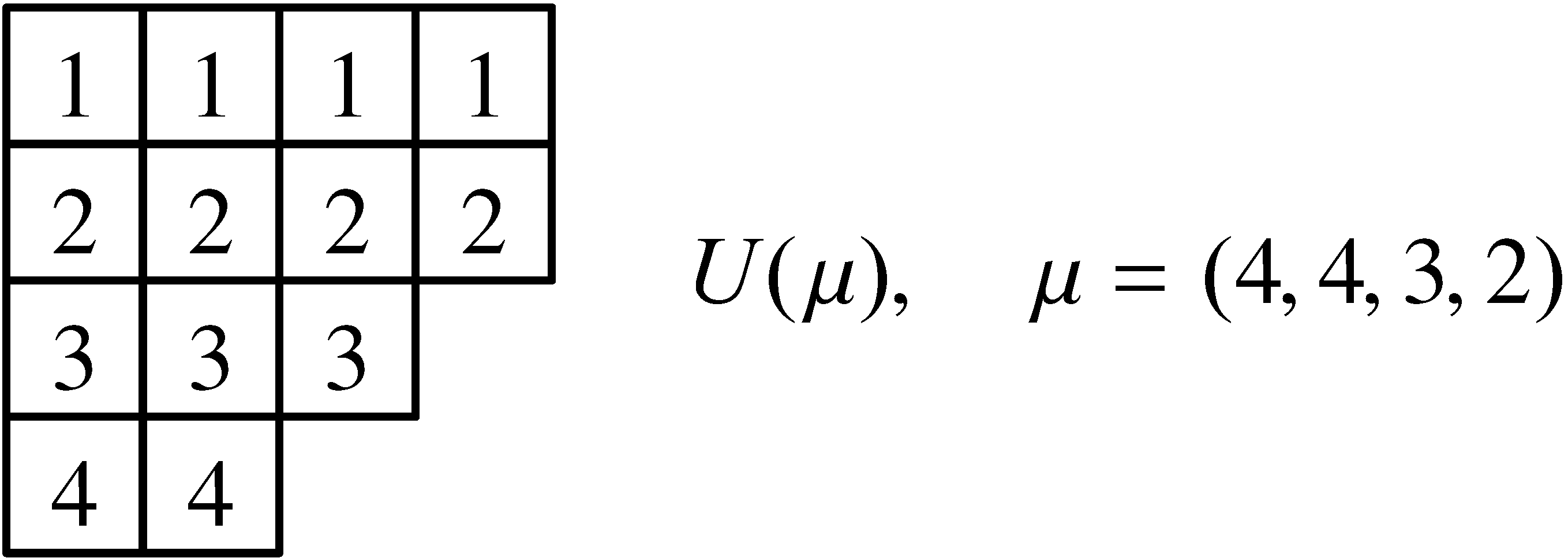
19. ábra
![]() minden véges dimenziós irreducibilis reprezentációjának egyetlen legnagyobb súlyvektora van. Két reprezentáció pontosan akkor izomorf, ha a legnagyobb súlyvektoruk súlya megegyezik. Ha
minden véges dimenziós irreducibilis reprezentációjának egyetlen legnagyobb súlyvektora van. Két reprezentáció pontosan akkor izomorf, ha a legnagyobb súlyvektoruk súlya megegyezik. Ha ![]() maximálisan
maximálisan ![]() sorból áll, akkor
sorból áll, akkor ![]() -nek minden
-nek minden ![]() reprezentációja egy irreducibilis reprezentáció a
reprezentációja egy irreducibilis reprezentáció a ![]() legnagyobb súllyal. Ezek
legnagyobb súllyal. Ezek ![]() összes irreducibilis polinomiális reprezentációi. Minden
összes irreducibilis polinomiális reprezentációi. Minden ![]() ,
, ![]() , esetén egyetlen
, esetén egyetlen ![]() legnagyobb súlyú irreducibilis reprezentációja létezik
legnagyobb súlyú irreducibilis reprezentációja létezik ![]() -nek, ez a
-nek, ez a ![]() tenzorszorzattal adható meg, ahol
tenzorszorzattal adható meg, ahol ![]() úgy, hogy
úgy, hogy ![]() minden
minden ![]() -re. Itt
-re. Itt ![]() és
és ![]() a
a ![]() ,
, ![]() 1-dimenziós reprezentáció.
1-dimenziós reprezentáció.
Ha adott két ![]() ,
, ![]() irreducibilis reprezentációja
irreducibilis reprezentációja ![]() -nek a
-nek a ![]() és
és ![]() ,
, ![]() , legnagyobb súllyal, akkor a
, legnagyobb súllyal, akkor a ![]() tenzorszorzat egy másik véges dimenziós holomorf reprezentációja
tenzorszorzat egy másik véges dimenziós holomorf reprezentációja ![]() -nek. A
-nek. A ![]() tenzorszorzat felbomlik irreducibilis reprezentációk direkt összegére, és az a szám
tenzorszorzat felbomlik irreducibilis reprezentációk direkt összegére, és az a szám ![]() , hogy egy adott
, hogy egy adott ![]() irreducibilis reprezentáció hányszor fordul elő ebben az összegben, független a felbontás választásától. Ezt nevezzük Littlewood-Richardson együtthatónak. Ez éppen a
irreducibilis reprezentáció hányszor fordul elő ebben az összegben, független a felbontás választásától. Ezt nevezzük Littlewood-Richardson együtthatónak. Ez éppen a ![]() alakú és
alakú és ![]() tartalmú Littlewood-Richardson ferde táblázatok száma. A (7) kvantumrelációt úgy definiáljuk, hogy akkor áll fenn, ha a
tartalmú Littlewood-Richardson ferde táblázatok száma. A (7) kvantumrelációt úgy definiáljuk, hogy akkor áll fenn, ha a ![]() irreducibilis reprezentáció egy másolata legalább egyszer előfordul a
irreducibilis reprezentáció egy másolata legalább egyszer előfordul a ![]() tenzorszorzatban, azaz ha
tenzorszorzatban, azaz ha ![]() .
.
A (7) reláció szimmetrikus alakját pedig úgy definiáljuk, hogy a
reláció akkor teljesül, ha ![]() tenzor szorzat tartalmaz egy nemtriviális
tenzor szorzat tartalmaz egy nemtriviális ![]() invariáns vektort.
invariáns vektort.
A saturation-sejtés a 4. állítás formájában a ![]() csoportra igaz.
csoportra igaz.
Irodalomjegyzék
- [1] W. Fulton, Young Tableaux, Cambridge Univ. Press, 1997.
- [2] A. Horn, Eingenvalues of sums of Hermitian matrices, Pacific J. Math. 12 (1962), 225–241.
- [3] A. A. Klyachko, Stable vector bundles and Hermitian operators, Selecta Math. (N.S.) 4 (1998), 419–445.
- [4] A. Knutson and T. Tao, The honeycomb model of
 tensor products I: Proof of the saturation conjecture, J. Amer. Math. Soc. 12 (1999), 1055–1090.
tensor products I: Proof of the saturation conjecture, J. Amer. Math. Soc. 12 (1999), 1055–1090. - [5] A. Knutson and T. Tao, Honeycombs and Sums of Hermitian Matrices, Notices in AMS, (2001), 175–186.
- [6] A. Knutson, T. Tao and C. Woodward, The honeycomb model of
 tensor products II: Facets of the Littlewood-Richardson cone, J. Amer. Math. Soc. 17 (2004), 19–48.
tensor products II: Facets of the Littlewood-Richardson cone, J. Amer. Math. Soc. 17 (2004), 19–48.









