Információk

 Aktuális szám: 8. szám 2018. június 

Mi is egy ... Higgs-nyaláb?

Mi is egy ... Higgs-nyaláb?

Egy Higgs-nyaláb nem más, mint egy holomorf vektornyaláb és egy ún. Higgs-mező együttese. Ezek a fogalmak Nigel Hitchin Riemann-felületek feletti önduális egyenletekről írt tanulmányában, illetve Carlos Simpson doktori értekezésében és egy későbbi, nem-abeli Hodge-elméleti munkájában tűntek fel először. A mérceelmélet egyenleteiben fellépő hasonló objektumok elnevezése nyomán Hitchin bevezette a Higgs-mező fogalmát. Ebben az összefüggésben a Higgs-mező olyan fizikai részecskéket ír le, mint például a Higgs-bozon. Simpson javaslatára a „Higgs-nyaláb” elnevezés együtt utal egy nyalábra és egy Higgs-mezőre.

A Higgs-nyalábok gazdag struktúrát hordoznak, ami olyan területeken játszik szerepet mint a mérceelmélet, a Kähler- és hiperkähler-geometria, felületek fundamentális csoportjainak ábrázolásai, az integrálható rendszerek elmélete, a nem-abeli Hodge-elmélet, a mátrixszorzatok Deligne—Simpson-problémája és újabban a tükörszimmetria és a Langlands-dualitás. Néhány területet ebben az írásban is érinteni fogunk.

Kezdjük a definícióval! A Higgs-nyaláb egy olyan $ (E,\phi)$ pár, ahol $ E$ holomorf vektornyaláb, a $ \phi$-vel jelölt Higgs-mező pedig olyan holomorf $ 1$-forma, ami az $ E$ endomorfizmusnyalábjából veszi fel az értékeit, továbbá kielégíti a $ \phi \wedge \phi=0$ összefüggést.

A legegyszerűbb esetekben a szóban forgó vektornyaláb komplex vonalnyaláb, míg a Higgs-mező holomorf 1-forma. Tekintsünk egy nem-abeli példát! Legyen $ E=K^{1/2} \oplus K^{-1/2}$, ahol $ K^{1/2}$ az a komplex vonalnyaláb, amelynek a négyzete éppen a Riemann-felület fölötti $ K$ kanonikus nyaláb (vagyis a holomorf $ 1$-formák nyalábja). Az $ E$ vektornyalábon lévő Higgs-mező ekvivalens egy $ \phi\colon E \longrightarrow E \otimes K$ nyalábleképezéssel. Így ezzel Higgs-mezők egy, kvadratikus differenciálok által paraméterezett családját kapjuk $ E$ felett, vagyis:


$\displaystyle \phi = \begin{pmatrix}0 & \sigma \\ 1 & 0 \end{pmatrix},$ (1)

 

ahol $ \sigma$ a $ K^2 \cong \operatorname{Hom}\left(K^{-1/2}, K^{1/2} \otimes K \right)$ vonalnyaláb szelése és $ 1$ pedig a $ \operatorname{Hom}\left(K^{1/2}, K^{-1/2} \otimes K \right)$ triviális nyaláb identitás szelése.

A Hodge-elméletben egy Riemann-sokaság de Rham kohomológiaosztályainak reprezentálására harmonikus differenciálformákat használunk, míg egy Hermite-féle sokaság (jelölje $ X$) Dolbeault kohomológia osztályait a $ \bar{\partial}$-harmonikus formák reprezentálják. Ha az $ X$-en létezik Kähler-metrika, akkor a valós és a komplex elmélet kompatibilis. Ez összekapcsolja a topologikus és a holomorf adatokat az$ X$sokaságon, és feltár egy további struktúrát a topologikus oldalon, pontosabban a $ H^k(X,\mathbb{C})$ kohomológiacsoportokon. Például $ k=1$-re azt kapjuk, hogy:

$\displaystyle H^1(X;\mathbb{C}) \cong H^{0,1}(X) \oplus H^{1,0} (X). $

Holomorf tekintetben $ H^{0,1}(X)$ leírja az $ X$ feletti holomorf vonalnyalábok deformációját, míg $ H^{1,0} (X)$ a holomorf $ 1$-formák tere. Így a holomorf adat egy $ (E, \phi$) párból jön, ahol $ E$vonalnyaláb $ \phi \in H^{1,0} (X)$ pedig Higgs-mező, vagyis együtt egy abeli Higgs-nyalábot határoznak meg. Topologikus szemszögből $ H^1(X;\mathbb{C})$ modellezi a $ \pi_1(X)$-ből $ \mathbb{C}^{*}$-ba menő homomorfizmusok terének érintőterét, ami ugyanaz, mint az $ X$ feletti lapos komplex vonalnyalábok tere.

A nem-abeli elméletben kicseréljük $ \mathbb{C}^{*}$-ot egy nemkommutatív Lie-csoportra, egészen pontosan valamely $ \operatorname{SL}(n,\mathbb{C})$ csoportra. A Hodge-elmélet topologikus vonatkozásában a $ \pi_1(X)$ fundamentális csoport $ \operatorname{SL}(n,\mathbb{C})$-reprezentációit kapjuk, vagy ekvivalens módon: az $ X$ feletti lapos vektornyalábokat. Corlette és Donaldson tétele az elmélet harmonikus aspektusáról ad számot: ha $ \pi_1(X)$ reprezentációja teljesen reducibilis, akkor a megfelelő lapos nyaláb (jelölje $ E$) ellátható harmonikus metrikák egy családjával (ehhez a Laplace-egyenlet egy megfelelő általánosítását kell megoldani). A másik oldalon, a holomorf interpretáció azt a tényt használja fel, hogy egy nyalábon a lapos struktúrák zérus görbületű konnexiókkal vannak definiálva. A harmonikus metrika két részre vágja a lapos konnexiókat: egy ferdén önadjungált (unitér) és egy önadjungált részre. Az előbbi antiholomorf komponense egy holomorf struktúrát ad meg $ E$-n, míg utóbbi egy holomorf, endomorfizmus értékű $ 1$-formát definiál, vagyis egy $ \phi$ Higgs-mezőt. Így az $ (E,\phi)$ holomorf adatok egy Higgs-nyalábot határoznak meg.

A következőkben áttekintjük a Higgs-nyalábok néhány jellemzőjét. Kezdjük Hitchin és Simpson tételével, amely kimondja, hogy amennyiben egy Higgs-nyalábhoz a fentiek szerint egy harmonikus metrikát rendelünk, akkor a nyalábnak ki kell elégítenie egy bizonyos stabilitási feltételt. Mindez, Corlette iménti tételével együtt, az $ X$ Kähler-sokaság feletti stabil Higgs-nyalábok és $ \pi_1(X)$ irreducibilis $ \operatorname{SL}(n,\mathbb{C})$-reprezentációi között ad egy megfeleltetést. Ez az állítás Narasimhan és Seshadri vektornyalábokra vonatkozó híres tételének, illetve annak Donaldson, Uhlenbeck és Yau általi általánosításának Higgs-nyalábos változata.

A Higgs-nyalábok fontos jellemzője egy $ \mathbb{C}^{*}$-hatás létezése, melyet a $ \lambda(E,\phi):=(E,\lambda \phi)$ módon definiálunk. A Higgs-nyalábok e hatás által fixen hagyott izomorfizmusosztályai a Hodge-struktúra komplex variációi (ez áll Simpson doktori értekezésének középpontjában). Utóbbiakon keresztül a Higgs-nyalábok erős megszorításokat adnak kompakt Kähler-sokaságok lehetséges fundamentális csoportjaira.

A Higgs-nyalábok másik központi tulajdonsága, hogy folytonos paramétereik vannak, vagyis olyan családokat alkotnak, amelyeket egy geometriai tér (valójában egy kvázi-projektív varietás) pontjai paramétereznek. Ez a jelenség akként ismert, hogy a Higgs-nyalábok egy modulusteret alkotnak. Bizonyos stabilitási tulajdonságtól függően, az ilyen terek konstruálásának egyik módját Mumford geometriai invariánselmélete (GIT) adja. Ha $ X$  Riemann-felület (amit mostantól végig felteszünk), akkor a korábban említett stabilitási tulajdonság pontosan megfelel a GIT-beli stabilitási fogalomnak. A nem-abeli Hodge-elmélet lényege, hogy így az $ X$ Riemann-felület fölötti stabil Higgs-nyalábok modulustere és $ \pi_1(X)$ irreducibilis $ \operatorname{SL}(n,\mathbb{C})$-reprezentációinak modulustere azonosítható. A megfelelő abeli elméletben minden Higgs-nyaláb stabil, és a holomorf $ 1$-formák tere a vonalnyalábok infinitezimális deformációs terének duálisa. Így a modulustér az $ X$ Jacobi-varietás koérintőnyalábja lesz ($ \operatorname{Jac}(X)=\left\{E\mid 0\mbox{~fokú vonalnyalábok}\right\}/\left\{\mbox{izo.}\right\} \simeq T^{2g}$ — a ford.). Az ennek megfelelő reprezentációk modulustere pedig a $ \operatorname{Hom}(\pi_1(X), \mathbb{C}^{*}) \cong (\mathbb{C}^{*})^{2g}$ karaktervarietással lesz egyenlő.

A modulustérnek egy harmadik leírása is adható, amikor elemeire a Hitchin-egyenletek megoldásaiként gondolunk. A Hitchin-egyenletek a $ \phi$ Higgs-mezőre és egy, az $ E$ nyaláb holomorf struktúrájával kompatibilis $ A$ $ \operatorname{SU}(n)$-konnexióra vonatkozó mérceelméleti egyenletek:

\begin{equation*}\begin{aligned} F_A + \left[ \phi,\phi^{*} \right] &=0, \\ \mathsf{d}_A'' \phi &=0. \end{aligned} \end{equation*}

Az egyenletekben $ F_A$ az $ A$ konnexió görbülete, $ \mathsf{d}_A'' \phi$ pedig a $ \phi$ kovariáns deriváltjának antiholomorf része. Hitchin olyan instantonok (anti-önduális egyenletek megoldásai) vizsgálatával jutott ezekhez az egyenletekhez, amelyek egy négydimenziós tér kétdimenziós szimmetriacsoportjával való hatására invariánsak. Az egyenletek egyszerre fejezik ki az $ A+\phi+\phi^{*}$ formulával megadott $ \operatorname{SL}(n,\mathbb{C})$-konnexió laposságát és a kapott lapos nyalábon adott metrika harmonikusságát, összekapcsolva a lapos nyalábokat és a Higgs-nyalábokat a fenti értelemben.

A négydimenziós eredet és az egyenletek szerkezete megmagyarázza a modulustér hiperkähler- struktúráját. Utóbbi egy olyan Riemann-metrika, ami Kähler-metrika három különböző komplex struktúrával is, amelyeket a kvaternió-azonosságokat kielégítő $ I$, $ J$ és $ K$ operátorok definiálnak. A Riemann-felület feletti Higgs-nyalábok modulustere (jelölje $ M$) egy nemkompakt hiperkähler-sokaság. A $ \mathbb{C}^{*}$-hatás megszorítása az -ra valamelyik Kähler-formára vonatkozó Hamilton-féle hatás lesz a modulustéren, a hozzá tartozó szimplektikus momentumleképezés pedig a Higgs-mező $ L^2$-normájából jön. Utóbbi leképezés egy perfekt Bott—Morse-függvényt határoz meg a modulustéren, és erős eszközt ad a modulustér topológiájának tanulmányozására.

Amellett, hogy a Higgs-mező egy kitüntetett Morse-függvényt biztosít, felelős a modulustér egy lényeges jellemzőjéért: a Hitchin-fibrálás létezéséért. Mivel $ \phi$ egy nyaláb fibrumainak endomorfizmusaiból veszi az értékeit, ezért kiszámítható a $ \det(\phi-\lambda I)$ kifejezés. Ennek a karakterisztikus polinomnak az együtthatói definiálják a Hitchin-fibrálást:

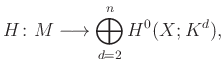
$\displaystyle H\colon M \longrightarrow \bigoplus_{d=2}^n H^0 (X; K^d), $

ahol $ K$ a kanonikus nyaláb $ X$-en. A Hitchin-fibrálás képhalmaza egy $ (\dim M)/2$ dimenziójú vektortér, generikus fibruma egy Abel-varietás, pontosabban egy ún. spektrál görbe Jacobi-varietása. Ez egy algebrai teljesen integrálható rendszerre szolgáltat példát.

A Hitchin-fibrálás egy kitüntetett szelése, melynek képe a $ \pi_1(X)$ csoport -beli reprezentációinak modulusterének egy komponensét adja, egy $ (n^2-1)(g-1)$ dimenziós komplex cellát alkot, ami $ n=2$-re a felület Teichmüller-terének felel meg. A Higgs-nyalábok pedig éppen a korábban tárgyalt $ 2$ rangú példák. Az (1) képletben a $ \sigma=0$ feltevéssel élve, majd a Hitchin-egyenletek egzisztenciatételét alkalmazva, a Riemann-felületek uniformizációs tételének új bizonyítását nyerjük.

Gyakorlatilag minden fent leírt eszköz alkalmazható, ha az $ \operatorname{SL}(n,\mathbb{C})$ csoportot kicseréljük egy $ G$ komplex, féligegyszerű Lie-csoportra. Az így nyert $ G$-Higgs-nyaláb elmélet holomorf eszközöket nyújt a $ \pi_1(X)$ csoport $ G$-beli, illetve $ G$ valós formáiba való reprezentációinak tanulmányozásához. Ez annak a jele, hogy még sokat tanulhatunk a Higgs-nyalábok elméletéből. Például Higgs-nyalábok, a topologikus mezőelméleten keresztül, szerepet játszanak a geometriai Langlands-program Kapustin—Witten interpretációjában. Végül megjegyezzük, hogy a Hitchin-egyenletek itt egy kétdimenziós szimmetriát indukálnak, épp úgy, amint Hitchin eredetileg származtatta az egyenleteit.

Irodalomjegyzék

[1] Az első két úttörő munka: N. J. HITCHIN, The self-duality equations on a Riemann surface, Proc. London Math. Soc. (3), 55 (1987) 59—126; és C. T. SIMPSON, Higgs bundles and local systems, Publ. Math. I. H. E. S. 75 (1992) 5—95.

 

[2] A későbbi eredményekhez lásd: S. BRADLOW, O. GARCíA-PRADA és P. B. GOTHEN, Surface group representations and $ U(p,q)$-Higgs bundles, J. Diff. Geom. 64 (2003) 111—170; és R. DONAGI és T. PANTEV, Langlands duality for Hitchin systems, Invent. Math. (3) 189 (2012) 653—735.

 

Steven B. Bradlow, Oscar Gracía-Prada, Peter B. Gothen

A cikk eredetileg a Notices of the American Mathematical Society folyóirat What is... rovatában jelent meg 2007-ben. Ez a fordítás a szerzők és az AMS engedélyével jelenik meg. A fordítást készítette: Ivanics Péter.

Steven B. Bradlow, Oscar García-Prada, and Peter B. Gothen,   WHAT IS...a Higgs Bundle? Notices Amer. Math. Soc. Vol.54 Num. 8. (2007 Sept) 980-981 ©2007 American Mathematical Society. http://www.ams.org/notices/200708/tx070800980p.pdf