A Gibbons—Hawking konstrukció
1. Bevezetés
Ebben az írásban a G. Gibbons és S. Hawking által megtalált aszimptotikusan lokálisan lapos gravitációs (anti-)insztanton-családot ismertetjük, és leírjuk ezek aszimptotikus viselkedését a sokaság végtelen távoli részén. A második szakaszban a differenciálgeometriában kevéssé járatos olvasó számára bevezetjük ezen egyenletek természetes nyelvezetét, az úgynevezett Riemann-sokaságok és ezek Riemann-féle görbületi tenzorának fogalmát. A harmadik szakaszban megadjuk a ![]() -sokaságok görbületi tenzorának felbontását, és bevezetjük a gravitációs anti-insztanton fogalmát. A negyedik szakaszban gravitációs anti-insztantonok két konstrukcióját mutatjuk meg, és leírjuk a kapott megoldások aszimptotikus viselkedését.
-sokaságok görbületi tenzorának felbontását, és bevezetjük a gravitációs anti-insztanton fogalmát. A negyedik szakaszban gravitációs anti-insztantonok két konstrukcióját mutatjuk meg, és leírjuk a kapott megoldások aszimptotikus viselkedését.
2. Riemann-sokaságok, Levi-Cività-konnexió, görbület
Legyen ![]() összefüggő szeparábilis Hausdorff-tér és
összefüggő szeparábilis Hausdorff-tér és ![]() . Azt mondjuk, hogy
. Azt mondjuk, hogy ![]() -en adott egy
-en adott egy ![]() -dimenziós differenciálható sokaság struktúra, ha létezik
-dimenziós differenciálható sokaság struktúra, ha létezik ![]() -beli nyílt halmazok olyan
-beli nyílt halmazok olyan ![]() családja, amelyre
családja, amelyre
és minden ![]() esetén létezik
esetén létezik
homeomorfizmus valamely nyílt ![]() halmazra, valamint minden
halmazra, valamint minden ![]() esetén a
esetén a
leképezés inverzével együtt differenciálható.
Legyen ![]()
![]() -dimenziós differenciálható sokaság és
-dimenziós differenciálható sokaság és ![]() . Ekkor
. Ekkor ![]() -nek az
-nek az ![]() -beli értintőtere az összes
-beli értintőtere az összes ![]() görbe halmaza valamely
görbe halmaza valamely ![]() esetén, amelyre
esetén, amelyre ![]() és valamely (ekvivalens módon, bármely)
és valamely (ekvivalens módon, bármely) ![]() -re
-re ![]() sima, a következő ekvivalenciareláció erejéig: két ilyen
sima, a következő ekvivalenciareláció erejéig: két ilyen ![]() görbe akkor és csak akkor ekvivalens egymással, ha valamely olyan
görbe akkor és csak akkor ekvivalens egymással, ha valamely olyan ![]() esetén, amelyre
esetén, amelyre ![]() , teljesül
, teljesül
Az ![]() -dimenziós
-dimenziós ![]() differenciálható sokaság
differenciálható sokaság ![]() -beli értintőtere egy
-beli értintőtere egy ![]() -dimenziós vektortér, amelyet
-dimenziós vektortér, amelyet ![]() -mel jelölünk. Egy sima vektormező
-mel jelölünk. Egy sima vektormező ![]() -en egy szelése az értintőnyalábnak, azaz egy
-en egy szelése az értintőnyalábnak, azaz egy
hozzárendelés, amelyre ![]() sima
sima ![]() -ban. Egy
-ban. Egy ![]() függvény deriváltja egy
függvény deriváltja egy ![]() vektormező mentén az az
vektormező mentén az az ![]() függvény, amelyre
függvény, amelyre
bármely ![]() -et reprezentáló
-et reprezentáló ![]() görbe esetén.
görbe esetén.
Egy konnexió ![]() -en egy olyan eljárás, ami két
-en egy olyan eljárás, ami két ![]() sima vektormezőhöz egy
sima vektormezőhöz egy ![]() vektormezőt rendel, teljesítve a következő feltételeket:
vektormezőt rendel, teljesítve a következő feltételeket:
- additivitás
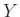 -ban: bármely
-ban: bármely 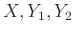 vektormezőkre
vektormezőkre

- linearitás
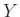 -ban skalármezők felett: bármely
-ban skalármezők felett: bármely 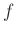 sima függvényre
sima függvényre 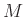 -en
-en
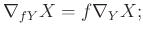
- additivitás
 -ben: bármely
-ben: bármely  vektormezőkre
vektormezőkre
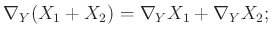
- Leibniz-szabály: bármely
 sima függvényre
sima függvényre  -en
-en
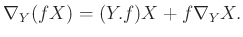
Legyenek ![]() sima vektormezők egy
sima vektormezők egy ![]() differenciálható sokaságon. Ekkor létezik egy olyan
differenciálható sokaságon. Ekkor létezik egy olyan ![]() sima vektormező
sima vektormező ![]() -en, hogy bármely
-en, hogy bármely ![]() sima függvényre
sima függvényre ![]() -en
-en
A ![]() vektormezőt
vektormezőt ![]() és
és ![]() Lie-zárójelének nevezzük. Egy
Lie-zárójelének nevezzük. Egy ![]() konnexió torziója az
konnexió torziója az ![]() irányokban a
irányokban a
mennyiség. Egy ![]() konnexiót torziómentesnek hívunk, ha minden
konnexiót torziómentesnek hívunk, ha minden ![]() sima vektormezők esetén
sima vektormezők esetén ![]() .
.
Egy Riemann-metrika egy ![]() -dimenziós
-dimenziós ![]() differenciálható sokaságon az
differenciálható sokaságon az ![]() értintőterein adott
értintőterein adott ![]() szimmetrikus pozitív definit bilineáris formák olyan
szimmetrikus pozitív definit bilineáris formák olyan
családja, hogy bármely ![]() sima vektormezők esetén
sima vektormezők esetén
sima függvény ![]() -ban. Egy Riemann-sokaság egy
-ban. Egy Riemann-sokaság egy ![]() páros, ahol
páros, ahol ![]() egy
egy ![]() -dimenziós differenciálható sokaság és
-dimenziós differenciálható sokaság és ![]() egy Riemann-metrika
egy Riemann-metrika ![]() -en. Legyen adott egy
-en. Legyen adott egy ![]() Riemann-sokaság. Ekkor bármely
Riemann-sokaság. Ekkor bármely ![]() sima görbének definiálhatjuk a hosszát az
sima görbének definiálhatjuk a hosszát az
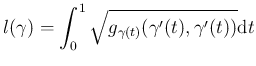
képlettel. Továbbá, bármely ![]() esetén definiálhatjuk az
esetén definiálhatjuk az ![]() és
és ![]() közötti távolságot a
közötti távolságot a
képlettel, ahol az infimumot az összes olyan ![]() sima görbére vesszük, amelyre
sima görbére vesszük, amelyre ![]() és
és ![]() . Ekkor
. Ekkor ![]() egy metrika
egy metrika ![]() -en; innen ered a „Riemann-metrika” elnevezés is. Innentől feltesszük, hogy az
-en; innen ered a „Riemann-metrika” elnevezés is. Innentől feltesszük, hogy az ![]() Riemann-sokaságból ezzel az eljárással nyert
Riemann-sokaságból ezzel az eljárással nyert ![]() metrikus tér teljes.
metrikus tér teljes.
Egy ![]() konnexiót kompatibilisnek mondunk egy
konnexiót kompatibilisnek mondunk egy ![]() Riemann-metrikával, ha bármely
Riemann-metrikával, ha bármely ![]() vektormező esetén teljesül, hogy
vektormező esetén teljesül, hogy
A Riemann-geometria főtétele szerint minden ![]() Riemann-sokaságon létezik pontosan egy torziómentes konnexió, amely kompatibilis
Riemann-sokaságon létezik pontosan egy torziómentes konnexió, amely kompatibilis ![]() -vel. Ezt a konnexiót az
-vel. Ezt a konnexiót az ![]() Riemann-sokaság Levi-Cività-konnexiójának nevezzük, és
Riemann-sokaság Levi-Cività-konnexiójának nevezzük, és ![]() -vel jelöljük. A Levi-Cività-konnexióból származtatható egy
-vel jelöljük. A Levi-Cività-konnexióból származtatható egy ![]() -tipusú
-tipusú ![]() tenzormező a
tenzormező a
szimmetrikus lineáris transzformációként. Végül, a Riemann-féle görbületi tenzorból származtatható a
Ricci-féle görbületi tenzormező a
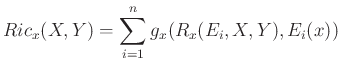
képlettel, ahol ![]() a
a ![]() euklideszi tér egy tetszőleges ortonormált bázisa. A Ricci-görbület tehát a Riemann-görbület nyoma az első és utolsó változójában. Az általános relativitás-elmélet (Riemann-féle) vákuum Einstein-egyenlete az eddigi jelölésekkel felírható a
euklideszi tér egy tetszőleges ortonormált bázisa. A Ricci-görbület tehát a Riemann-görbület nyoma az első és utolsó változójában. Az általános relativitás-elmélet (Riemann-féle) vákuum Einstein-egyenlete az eddigi jelölésekkel felírható a
alakban, ahol ![]() (a
(a ![]() metrika úgynevezett Einstein-állandója).
metrika úgynevezett Einstein-állandója).
3. Gravitációs anti-insztantonok
Az Einstein-egyenlet a ![]() -dimenziós téridő fizikai modelljéből származó matematikai egyenlet, amelynek ismertek érdekes megoldásai. Ezek ismertetésétől azonban most eltekintünk, mert cikkünk szorosabban vett témája egy ehhez kapcsolódó, ám matematikailag jobban kezelhető egyenlet felírása és megoldásainak vizsgálata. Ebben a szakaszban az
-dimenziós téridő fizikai modelljéből származó matematikai egyenlet, amelynek ismertek érdekes megoldásai. Ezek ismertetésétől azonban most eltekintünk, mert cikkünk szorosabban vett témája egy ehhez kapcsolódó, ám matematikailag jobban kezelhető egyenlet felírása és megoldásainak vizsgálata. Ebben a szakaszban az ![]() Riemann-sokaság dimenziója
Riemann-sokaság dimenziója ![]() .
.
Legyen adott egy ![]() Riemann-sokaság. Ekkor, minden
Riemann-sokaság. Ekkor, minden ![]() érintőtéren kapunk egy
érintőtéren kapunk egy ![]() térfogati formát, azaz egy alternáló
térfogati formát, azaz egy alternáló
multilineáris leképezést: egy ![]() ortonormált bázisra
ortonormált bázisra
Továbbá, minden ![]() pároshoz hozzárendelhetünk egy
pároshoz hozzárendelhetünk egy ![]() térfogati formát a
térfogati formát a
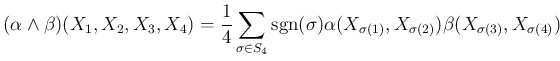
képlet által. A Hodge-operátor egy ![]() -dimenziós
-dimenziós ![]() Riemann-sokaságon az a
Riemann-sokaságon az a
leképezés, amelyre minden ![]() esetén
esetén
Könnyen látható, hogy ![]() , tehát
, tehát ![]() felbomlik
felbomlik
alakban, ahol
a Hodge-operátor ![]() -sajátértékhez tartozó altere. Az
-sajátértékhez tartozó altere. Az ![]() alterek egyenként
alterek egyenként ![]() -dimenziósak, és elemeiket rendre önduális illetve anti-önduális
-dimenziósak, és elemeiket rendre önduális illetve anti-önduális ![]() -formáknak nevezzük.
-formáknak nevezzük.
Bontsuk fel a Riemann-féle görbületi tenzort ezen felbontás szerinti tömb-mátrixokra. Ehhez előbb írjuk fel a Ricci-görbületet a nyoma és nyom-nélküli része összegeként:
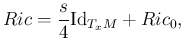
ahol
az ![]() skalár-görbülete,
skalár-görbülete, ![]() pedig a nyom-nélküli Ricci-görbület. Kiderül, hogy
pedig a nyom-nélküli Ricci-görbület. Kiderül, hogy ![]() felcseréli az
felcseréli az ![]() altereket, és
altereket, és ![]() alakja erre a felbontásra nézve a következő:
alakja erre a felbontásra nézve a következő:

Az itt bevezetett ![]() tenzorokat
tenzorokat ![]() pozitív illetve negatív Weyl-tenzorának nevezzük. Azt mondjuk, hogy egy
pozitív illetve negatív Weyl-tenzorának nevezzük. Azt mondjuk, hogy egy ![]() Riemann-féle
Riemann-féle ![]() -sokaság gravitációs anti-insztanton, ha teljesül
-sokaság gravitációs anti-insztanton, ha teljesül
Az első egyenlet éppen az Einstein-egyenlet ![]() állandóval, a második pedig a görbület anti-öndualitását írja elő. Az egyenletrendszer elnevezése is ezt tükrözi: a gravitációs jelző arra utal, hogy az Einstein-egyenlet a gravitációt írja le, míg az anti-insztanton általános elnevezés anti-öndualitási egyenletek megoldásaira. Itt tehát e két egyenletrendszer csatolásából álló rendszert vizsgáljuk. A gravitációs insztanton fogalma teljesen hasonló a gravitációs anti-insztantonéhoz, azzal a különbséggel hogy ekkor
állandóval, a második pedig a görbület anti-öndualitását írja elő. Az egyenletrendszer elnevezése is ezt tükrözi: a gravitációs jelző arra utal, hogy az Einstein-egyenlet a gravitációt írja le, míg az anti-insztanton általános elnevezés anti-öndualitási egyenletek megoldásaira. Itt tehát e két egyenletrendszer csatolásából álló rendszert vizsgáljuk. A gravitációs insztanton fogalma teljesen hasonló a gravitációs anti-insztantonéhoz, azzal a különbséggel hogy ekkor ![]() -ról követeljük meg ugyanazt mint fent
-ról követeljük meg ugyanazt mint fent ![]() -ról; e két egyenlet kicserlélődik egymással a sokaság irányításának megfordítása esetén, ezért az előjelnek ebben az elméletben nincs fontos szerepe.
-ról; e két egyenlet kicserlélődik egymással a sokaság irányításának megfordítása esetén, ezért az előjelnek ebben az elméletben nincs fontos szerepe.
Amennyiben ![]() teljesít egy egyszeresen összefüggőségnek nevezett globális topológiai tulajdonságot, akkor kiderül, hogy
teljesít egy egyszeresen összefüggőségnek nevezett globális topológiai tulajdonságot, akkor kiderül, hogy ![]() akkor és csak akkor gravitációs anti-insztanton, ha
akkor és csak akkor gravitációs anti-insztanton, ha ![]() -nak létezik egy globális
-nak létezik egy globális ![]() -párhuzamos bázisa — az ezzel a tulajdonsággal rendelkező Riemann-féle
-párhuzamos bázisa — az ezzel a tulajdonsággal rendelkező Riemann-féle ![]() -sokaságokat hiperkähler
-sokaságokat hiperkähler ![]() -sokaságoknak nevezzük.
-sokaságoknak nevezzük.
4. Gravitációs anti-insztantonok konstrukciói: tegez-varietások, Eguchi—Hanson és Gibbons—Hawking terek
M. Atiyah, V. Drinfeld, N. Hitchin és Y. Manin egy 1978-as konstrukciója, az úgynevezett ADHM-konstrukció [1], illetve annak P. Kronheimer és H. Nakajima általi továbbfejlesztése [5] egy általános módszert ad hiperkähler-sokaságok konstruálására. Az így kapott sokaságok általános neve tegez-varietás. A tegez-varietások konstrukciójának kiinduló adata egy véges ![]() gráf,
gráf, ![]() csúcspont- és
csúcspont- és ![]() élhalmazzal, egy
élhalmazzal, egy
függvény (az úgynevezett dimenzió-vektor), valamint egy rá merőleges
vektor. Minden véges ![]() gráfhoz,
gráfhoz, ![]() dimenzió-vektorhoz és
dimenzió-vektorhoz és ![]() vektorhoz tartozik tehát egy
vektorhoz tartozik tehát egy ![]() tegez-varietás egy Riemann-metrikával, amely kellően általános
tegez-varietás egy Riemann-metrikával, amely kellően általános ![]() esetén egy sima hiperkähler-sokaság. Speciálisan, legyen
esetén egy sima hiperkähler-sokaság. Speciálisan, legyen ![]() egy
egy ![]() -hosszú ciklus és a
-hosszú ciklus és a ![]() dimenzió-vektor rendeljen
dimenzió-vektor rendeljen ![]() minden csúcsához
minden csúcsához ![]() -et (ahogy az ábra is mutatja), valamint legyen
-et (ahogy az ábra is mutatja), valamint legyen ![]() kellően általános.
kellően általános.
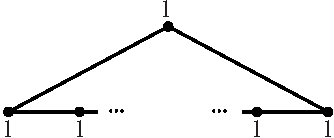
1. ábra: A ciklikus ![]() gráf
gráf
Kiderül, hogy az ezekkel a választásokkal kapott ![]() tegez-varietás egy olyan
tegez-varietás egy olyan ![]() -dimenziós gravitációs anti-insztanton, amelynek alaptere diffeomorf az
-dimenziós gravitációs anti-insztanton, amelynek alaptere diffeomorf az
egyenlettel definiált ![]() egyszerű komplex felület-szingularitás kisimításával. Az így kapott
egyszerű komplex felület-szingularitás kisimításával. Az így kapott ![]() -dimenziós gravitációs anti-insztantonokat Eguchi—Hanson tereknek nevezzük.
-dimenziós gravitációs anti-insztantonokat Eguchi—Hanson tereknek nevezzük.
A tegez-varietások egyik alapvető tulajdonsága, hogy nem kompaktak, azonban a ![]() metrika viselkedése valamely
metrika viselkedése valamely ![]() kompakt halmazon kívül jól behatárolt, úgynevezett aszimptotikusan lokálisan euklideszi (ALE). Ennek a fogalomnak a megértéséhez vegyük észre, hogy a
kompakt halmazon kívül jól behatárolt, úgynevezett aszimptotikusan lokálisan euklideszi (ALE). Ennek a fogalomnak a megértéséhez vegyük észre, hogy a ![]() -dimenziós euklideszi tér metrikája az origón kívül előáll
-dimenziós euklideszi tér metrikája az origón kívül előáll
alakban, ahol ![]() az origótól mért távolság,
az origótól mért távolság, ![]() pedig
pedig ![]() megszorítása az
megszorítása az ![]() egységgömbre. Ez az azonosság azt a szemléletesen nyilvánvaló tényt fejezi ki, hogy az
egységgömbre. Ez az azonosság azt a szemléletesen nyilvánvaló tényt fejezi ki, hogy az ![]() -sugarú gömbfelület metrikája
-sugarú gömbfelület metrikája ![]() -szerese az egység-sugarú gömbének. Ezt általánosítva azt mondjuk, hogy egy
-szerese az egység-sugarú gömbének. Ezt általánosítva azt mondjuk, hogy egy ![]() nem-kompakt Riemann-féle
nem-kompakt Riemann-féle ![]() -sokaság aszimptotikusan lokálisan euklideszi, ha valamely
-sokaság aszimptotikusan lokálisan euklideszi, ha valamely ![]() kompakt halmazra
kompakt halmazra
valamely ![]() -dimenziós
-dimenziós ![]() Riemann-sokaságra, és a metrikák között áll a
Riemann-sokaságra, és a metrikák között áll a
aszimptotikus egyenlőség. Az Eguchi—Hanson terek metrikája tehát teljesíti ezt a feltételt, ![]() választással.
választással.
Analitikus szempontból az aszimptotikusan lokálisan euklideszi terek a végtelenben nagyon természetes viselkedésűek, mert hasonlítanak az euklideszi terekre. Léteznek azonban másfajta aszimptotikus viselkedésű gravitációs anti-insztantonok is. Ezek közül több szempontból az úgynevezett aszimptotikusan lokálisan lapos (ALF) terek lényegesek. Ezen terek aszimptotikus viselkedése a következő: valamely ![]() kompakt halmazra
kompakt halmazra
valamely ![]() -dimenziós
-dimenziós ![]() Riemann-sokaságra, továbbá
Riemann-sokaságra, továbbá ![]() fibrálódik egy
fibrálódik egy ![]() Riemann-felület felett
Riemann-felület felett ![]() körvonal-fibrumokkal, a metrika pedig valamely
körvonal-fibrumokkal, a metrika pedig valamely ![]() skalárra teljesíti a
skalárra teljesíti a
aszimptotikus egyenlőséget. Szemléletesen ez azt jelenti, hogy ha tekintjük az ![]() távolságra levő
távolságra levő ![]() sokaságot, akkor nem a teljes
sokaságot, akkor nem a teljes ![]() metrikája szorzódik meg
metrikája szorzódik meg ![]() -tel, hanem annak csak egy rögzített
-tel, hanem annak csak egy rögzített ![]() -dimenziós irányba eső része, a maradék
-dimenziós irányba eső része, a maradék ![]() -dimenziós rész átmérője pedig tart
-dimenziós rész átmérője pedig tart ![]() -hoz ahogy
-hoz ahogy ![]() tart a végtelenbe. Fizikailag ezen
tart a végtelenbe. Fizikailag ezen ![]() érték (egy állandó erejéig) a megoldás hőmérsékletének inverzeként interpretálható.
érték (egy állandó erejéig) a megoldás hőmérsékletének inverzeként interpretálható.
Aszimptotikusan lokálisan lapos gravitációs anti-insztantonokat konstruálni bonyolultabb, mint aszimptotikusan lokálisan euklideszieket. Az első ilyen konstrukciót G. Gibbons és S. Hawking írta le [3,4]. A konstrukció a következő: legyen ![]() véges sok, egymástól különböző
véges sok, egymástól különböző ![]() pont komplementere és
pont komplementere és ![]() egy harmonikus függvény, amelyre
egy harmonikus függvény, amelyre
![$\displaystyle \left[ \frac{*{\operatorname{d}}V}{2\pi} \right] \in H^2(U, \mathbb{Z})
$](/images/stories/latex/javitasszaboszilardhawking/img27.png)
egész kohomológia-osztály. (A képletben szereplő ![]() a
a ![]() -dimenziós Hodge-operátor.) Ez a feltétel felfogható egy kvantálási feltételként. A Chern—Weil elmélet szerint létezik egy
-dimenziós Hodge-operátor.) Ez a feltétel felfogható egy kvantálási feltételként. A Chern—Weil elmélet szerint létezik egy ![]() -nyaláb
-nyaláb ![]() felett valamely
felett valamely ![]() totális térrel, valamint egy
totális térrel, valamint egy ![]() konnexió-forma
konnexió-forma ![]() -en, amelyre
-en, amelyre
Ekkor, ![]() -en a
-en a
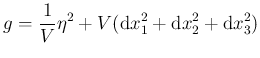
metrika gravitációs anti-insztanton, amely kiterjed a ![]() pontokra. Ezen konstrukció
pontokra. Ezen konstrukció
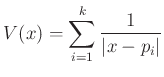
választással visszaadja a ![]() véges csoporthoz (pontosabban, az
véges csoporthoz (pontosabban, az ![]() szingularitáshoz) tartozó Eguchi—Hanson tereket. Minden
szingularitáshoz) tartozó Eguchi—Hanson tereket. Minden ![]() esetén a
esetén a
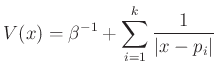
választás azonban aszimptotikusan lokálisan lapos teret eredményez ugyanezen sima sokaságon.
Ilyen értelemben, a Gibbons—Hawking terek általánosításai a már korábbról ismert és aszimptotikusan egyszerűbb viselkedésű aszimptotikusan lokálisan euklideszi gravitációs anti-insztantonoknak. Számos azóta született matematikai-fizikai eredmény (például [2,6]) azt mutatja, hogy ezek a megoldások sok szempotból alapvetőbb jelentőségűek aszimptotikusan lokálisan euklideszi társaiknál. Ezen elméletek leírása azonban már túlmutat jelen cikk keretein.
Irodalomjegyzék
- [1] M. Atiyah, V. Drinfeld, N. Hitchin, Y. Manin Construction of Instantons, Physics Letters, 65A (1978), 185—187.
- [2] A. Braverman, M. Finkelberg, H. Nakajima Towards a mathematical definition of Coulomb branches of
 -dimensional
-dimensional 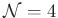 gauge theories, II., https://arxiv.org/abs/1601.03586
gauge theories, II., https://arxiv.org/abs/1601.03586 - [3] G. Gibbons, S. Hawking Graviational multi-instantons, Physics Letters B 78 (1978), 430—432.
- [4] G. Gibbons, S. Hawking Classification of Gravitational Instanton symmetries, Comm. Math. Phys. 66 (1979), 291—310.
- [5] P. Kronheimer, H. Nakajima Yang—Mills instantons on ALE graviational instantons, Math. Ann. 288 (1990), 263—307.
- [6] E. Witten Geometric Langlands From Six Dimensions, https://arxiv.org/abs/0905.2720
Szabó Szilárd
BME Matematikai Intézet, Geometria Tanszék
https://geometria.math.bme.hu/szabo-szilard









