Információk

 Aktuális szám: 4. szám 2017. június 

Diofantosz és a diofantikus egyenletek

Diofantosz és a diofantikus egyenletek

A 2016-os Abel díjas Andrew Wiles számos jelentős eredménnyel gazdagította a matematikát, de a világhírt a nagy Fermat-tétel bizonyítása hozta meg számára: ha $ n>2$, akkor az $ x^n+y^n=z^n$ egyenletnek nincsen olyan megoldása, ahol $ x,y,z$ zérustól különböző egészek.

Fermat ezt az állítást Diofantosz Aritmetikájának olvasása közben jegyezte fel. Az állítás, hogy az $ x^n+y^n=z^n$ egyenletnek nincs pozitív egész megoldása, könnyen érthető, de a bizonyítás évszázadokba telt.

Az Aritmetika Fermat jegyzeteivel ellátott kiadásából. A híres bejegyzés: “Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.” Avagy Bródy Ferenc míves fordításában: „Nincsen mód viszont felosztani köböt két köbre, sem négyzetes négyzetet két négyzetes négyzetre, és általában a négyzeten túl a végtelenig semmiféle hatványt két ugyanolyan nevezetűre; mely dolognak igazán csudálatos bizonyítását találtam. Szűkebb a margó, semhogy befogadná.”

De ki volt Diofantosz? Miről szólt az Aritmetika, és mi motiválta Fermat-t a híres megjegyzésre?

Az első kérdésre nincs kielégítő válaszunk. Sem Diofantoszról, sem tanárairól, sem tanítványairól nincsenek adataink. Ami biztos, hogy az i.e. 2. század és az i.sz. 4 sz. között élt, valószínűleg az i. sz. 2-3. században.

Diofantoszról a következő rejtvény maradt fenn. Az olvasóra bízzuk, hogy megfejtse, hány évet élt a nagy matematikus, ha az alábbiakat tudjuk róla:

Itt porlad Diofantosz mester, sírköve rajta.
Olvasd, közli veled, mily nagy a kor mit elért.
Élete egyhatodában gyermek volt, s a kamaszkor épp a tizenketted része az éveinek.
Számold rá a hetedrészt, ekkor házasodott meg.
Erre öt esztendőt, s megszületett a fia.
Ó jaj, szörnyű csapás ha fiunk megelőz a halálban!
Csak felennyi időt mért a fiúnak a sors mint neki.
Végül hogy négy év eltelt a magányban, várta a révész már, s átevezett vele is.

Diofantosz fő műve, az Aritmetika, témájában, eszközeiben és kifejezésmódjában is teljesen eltér az általunk ismert klasszikus görög matematikától. Az eredetileg 13 kötetből csupán 6 maradt fenn görögül, további példányok arab nyelven kerültek elő 1968-ban. Az arab könyvek feladatai más számozásúak, alkalmanként különböznek is. A görög nyelvű kötetek nagy valószínűséggel Hüpátia kommentárjai az eredetiről. (Heath: A history of Greek mathematics.)

Hüpátia Raffaello vatikáni freskóján. (Vagy nem.) Hüpátia (i.sz. 360 körül-415). Egy kortársa, Konstantinápolyi Szókratész egyháztörténeti leírása szerint „élt ebben az időben Alexandriában egy hölgy, Hüpátia, Theon filozófus lánya, aki oly sikereket ért el az irodalom és a tudományok terén, hogy jóval előtte járt minden kortárs filozófusnak. Platón és Plótinosz iskoláját kijárva, a filozófia alapelveit tanította diákjainak, akik közül sokan messze földről érkeztek.” Az egyik ilyen diákja, Kürénei Szünésziusz, későbbi püspök, így írt egy levelében neki: „Legnagyobb veszteségem, hogy nem lehetek az ön isteni szellemének közelében”. Hüpátia munkái is elvesztek, csak az Aritmetika átdolgozása maradt fenn.

A közhiedelemmel ellentétben Diofantosz elfogadott racionális számokat is megoldásként, mint a II. könyv híres 8. feladatában is, ami Fermat-t a híres margójegyzetre sarkallta. Habár megoldásként csak pozitív számokat fogadott el, számolás közben minden fenntartás nélkül használt negatív számokat is, tehát az elsők között ismerte fel a racionális számtest technikai előnyeit.

Amikor a XVI. században Európában újra felfedezték Diofantosz munkáit, az egyik első olvasója Bombelli olasz matematikus volt. Ő az Aritmetikában szereplő problémák jelentős részét beépítette Algebra című könyvébe, de a negatív számok használatából inspirációt merítve komplex számokat is használt harmadfokú egyenletek megoldására. Például az $ x^3=15x+4$ egyenlet megoldására a Cardano-féle képlet az $ x=\sqrt[3]{2+11i}+\sqrt[3]{2-11i}$ komplex számot adja. Bombelli megmutatta, hogy ez értelmezhető 4-ként (ami egy nyilvánvaló megoldás).

Diofantosz egy mai szemmel ugyan kezdetlegesnek tűnő algebrai jelölésrendszert használt, ám ez jelentős előrelépés volt a hagyományos körmondatokban leírt algebrai konstrukciókhoz képest. Pl. a változót $ \zeta$-val, a négyzetét $ \Delta^\nu$-vel jelölte. A negatív előjelre a $ \psi$ megfordítottját, vagyis $ \pitchfork$-t használta. Ugyanakkor ezzel a jelöléssel csak egy változó hatványait tudta jelölni, ezért ha további paraméterek jelentek meg, azokat mindig konkrét számnak választotta.

Így a XIX. században már sok olvasó számára tűnthetett úgy, hogy a könyv ad hoc trükkök gyűjteménye, és a többség egyetértett Hankel szavaival, aki szerint „100 probléma tanulmányozása után sem fogja tudni megoldani a 101-edik problémát”. Pedig ez távolról sincs így, a jelölésrendszeren és a racionális számtest használatán túlmutatóan is alapvető módszerek jelentek meg az Aritmetikában, amit alább két fontos példával is illusztrálunk.

Az első példa a fent említett II. könyv 8. feladata, ami Fermat-t híres sejtése megfogalmazására sarkalta. „Propositum quadratum dividere in duos quadratos...” azaz „Osszunk egy négyzetet két négyzet összegére”. Diofantosz megoldása (a fenti képen látható latin szövegben az $ N$ szám négyzetét $ Q$ jelöli, mi ehelyett a mai $ N^2$ jelölést alkalmazuk) a következő.

Legyen a négyzet 16. Legyen az egyik oldal $ N^2$, tehát a másik $ 16-N^2$. Ez utóbbinak négyzetnek kell lennie. Egy olyan négyzetet képezek, amelynek oldala az $ N$ tetszőleges többszöröse a(z eredeti) négyzet oldalával csökkentve. Ez $ 2N-4$1. Így ez a négyzet $ 4N^2+16-16N$. Ezt egyenlővé teszem $ 16-N^2$-tel. Mindkét oldalhoz hozzáadok $ N^2+16N$-t és kivonok $ 16$-t. Így $ 5N^2=16N$ adódik, amiből tehát $ N=16/5$ következik. Tehát az egyik szám $ \frac{256}{25}$, a másik pedig $ \frac{144}{25}$. A két szám összege 16 és mindkettő négyzet.

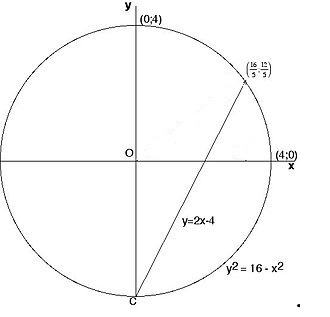
Diofantosz szelő módszere

A megoldás a koordináta-geometria nyelvén jobban megérthető. Az $ x^2+y^2=16$ körön keresünk olyan pontot amelynek mindkét koordinátája (pozitív) racionális szám. A nyilvánvaló $ (0,-4)$ ponton át indítsunk egyenest, pl. Diofantoszt követve legyen ez az egyenes az $ y=2x-4$ egyenlettel megadva. Ez az egyenes két pontban metszi a kört, a $ (0,-4)$ pontban, és a $ (16/5,12/5)$ pontban.

A módszer tetszőleges racionális meredekségű egyenesre ad egy új pontot. Ha $ y=\frac{m}{n}x-4$ akkor a másik metszéspont koordinátái egyszerűen kifejezhetők $ m,n$ segítségével. Az érdeklődő olvasó $ 16$ helyett $ 1$-et véve jobb oldalnak, az $ x^2+y^2=1$ megoldásait kifejezheti a $ (0,-1)$ ponton átmenő $ \frac{m}{n}$ meredekségű egyenest használva. Ily módon megadhatja az összes pitagoraszi számhármast, hiszen $ a^2+b^2=c^2$ esetén $ x=a/c$ és $ y=b/c$ racionális megoldásai az $ x^2+y^2=1$ egyenletnek.

A következő feladat megoldásának geometriai tartalma még érdekesebb.

IV. Könyv. 24. feladat. Bontsunk egy számot két részre, hogy a szorzatuk egy köb mínusz az oldal2. Diofantosz az „egy számot” 6-nak választja, így az

$\displaystyle y(6-y)=x^3-x $

 

egyenletet kapja.

 

Ennek nyilvánvaló megoldása $ x=-1$, $ y=0$. Nem véletlen tehát, hogy Diofantosz megint így gondolkodik: Az $ x$ szám legyen az $ y$ egy többszöröse eggyel csökkentve, azaz $ x=ay-1$. Ezután megkeresi $ a$ azon értékét amikor $ (ay-1)^3-(ay-1)$-ben $ y$ együtthatója $ 6$. Ez akkor áll fenn, ha $ a=3$. Ekkor $ 6y-y^2=(3y-1)(3y-2)3y$, azaz

$\displaystyle -y^2=27y^3-27y^2. $

 Tehát $ y=26/27$ és $ x=17/9$.

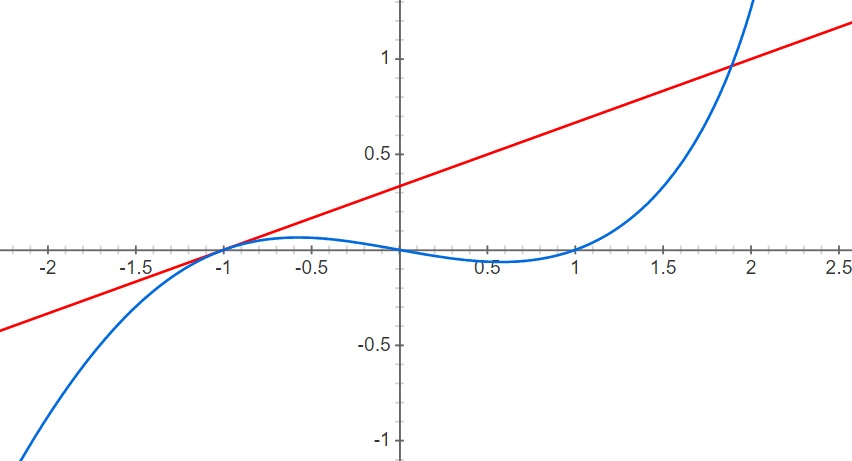
Diofantosz érintő módszere

Talán az a legmeglepőbb az algebrai konstrukció ábráján, hogy Diofantosz itt egy görbe érintőjét konstruálja meg tisztán algebrai eszközökkel.

Az érintő-egyenes és a harmadfokú görbe metszéspontjai olyan racionális együtthatós harmadfokú polinomra vezetnek, aminek $ y=0$ kétszeres gyöke, így a harmadik gyöknek is racionálisnak kell lennie. Ez ismét csak egy általános módszer, aminek mélységét csak a XX. században, az elliptikus görbék tanulmányozásával értettük meg. Ezek a görbék (lásd lejjebb) megkerülhetetlen szerepet játszottak Fermat sejtésének megoldásában.

Érdekes módon Fermat (aki Descartes mellett a koordináta-geometria egyik megalkotója is volt), Diofantoszt olvasva vezette be a „közelítőleg egyenlő” fogalmát. Fermat a következő okoskodást használta maximumszámításhoz. Ha az $ f(x)$ függvénynek maximuma van $ x$-ben, akkor $ f(x)\simeq f(x+e)$ közelítőleg egyenlő. Például, ha $ f(x)=bx-x^2$, akkor az $ f(x+e)-f(x)=(b+2x)e+e^2\simeq 0$ közelítő egyenlőség akkor állhat fenn, ha $ b+2x=0$. Fermat „levezetése” komoly ellenállásba ütközött. A pontosítás kísérlete, a végtelenül kicsiny mennyiségek bevezetése, ugyan nem oldotta meg a logikai problémákat, de megfelelő nyelvet teremtett a dinamikusan változó mennyiségek leírására, és több mint 200 évig dominálta az analízist.

Visszatérve a harmadfokú egyenletekkel megadható görbékre, már Newton belátta, hogy ha egy ilyen egyenletknek van legalább egy racionális pontja (azaz egy olyan pont aminek mindkét koordinátája racionális szám, és „rajta van a görbén”, azaz kielégíti az egyenletet), akkor az a változók egyszerű helyettesítése után, megfelelő $ A,B$ konstansokkal

$\displaystyle y^2=x^3+Ax+B $

alakra hozható. Például a fenti IV. 28. feladat esetén, $ y$ helyére $ y-3$-at, $ x$ helyére $ -x$-et írva az

$\displaystyle y^2=x^3-x+9 $

egyenletet kapjuk.

Az ilyen típusú egyenletek által megadott görbét elliptikus görbének nevezzük, ha az $ x^3+Ax+B$ harmadfokú polinom gyökei különbözőek, mert Weierstrass megmutatta, hogy ezek a görbék az Euler és Abel által tanulmányozott ú.n. elliptikus függvényekkel paraméterezhetők.

A XX. század derekán Poincaré észrevette, hogy a Diofantosz által használt szelő-érintő konstrukció az elliptikus görbe pontjain csoport struktúrát eredményez. Ehhez ki kell egészíteni a görbét egy $ [0]$ végetelen távoli ponttal; a függőleges egyenesek (és csak ezek) ugyanis csak két pontban metszenék a görbét, és a projektív geometria elvei alapján ezeknek a párhuzamos egyeneseknek a végtelen távoli közös metszéspontját adjuk a görbéhez.

Ezzel a kiterjesztéssel a következő műveletet képezhetjük. Legyen $ P_1(x_1,y_1)$ és $ P_2(x_2,y_2)$ két pont a görbén. Vegyük a $ P_1$ és $ P_2$ pontokon átmenő szelőt, vagy ha $ P_1=P_2$, akkor a pontbeli érintőt. Ha az így kapott egyenes a $ P_3(x_3,y_3)$ pontban metszi újra a görbét, legyen

$\displaystyle P_1\boxplus P_2=(x_3,-y_3). $

 

(Vegyük észre, hogy ez épp a $ P_3$ pont tükörképe az $ x$-tengelyre nézve.) Ha pedig a kapott egyenes függőleges, azt mondjuk majd, hogy $ P_1\boxplus P_2=[0]$. Az eredményül kapott $ \boxplus$ egy kommutatív, asszociatív művelet, amire nézve a görbe pontjai a végtelen távoli ponttal kiegészítve csoportot alkotnak. Az $ y^2=x^3-x+9$ példán illusztrálva a diofantoszi konstrukció a $ P(0,3)$ pontra a $ P\boxplus P$ pontot számítaná ki.

Ennek a csoportnak a vizsgálata jelentős szerepet játszott a XX. század számelméletében. Ez a konstrukció, Diofantosz szellemében, bármely test (akár véges test) felett is megvalósítható. Egy talán váratlan meglepetésként, ezek a véges elliptikus görbék komoly szerepet játszanak modern kriptográfiai (vagyis titkosírás) alkalmazásokban.

Elliptikus görbék hozták meg a Fermat sejtés bizonyítását is. Frey (illetve korábban Helleougarch) javasolta, hogy a Fermat egyenlet egy hipotetikus $ A^n+B^n=C^n$ megoldása esetén az

$\displaystyle y^2=x(x-A^n)(x-B^n) $

 elliptikus görbe nem lehetne moduláris. Ennek a gondolatnak a kifejtése külön cikket igényel, ami a következő számunkban jelenik majd meg.

 A debreceni egyetem algebra és számelmélet tanszékének munkatársai

Végezetül pár szóban meg kell említenünk a diofantikus egyenletek hazai fellegvárát, a debreceni egyetem számelméleti kutatócsoportját. Ezt az iskolát Győry Kálmán teremtette meg, aki Alan Baker Fields-díjas matematikus módszerét fejleszette tovább. Megemlítendő, hogy Győry Kálmánon kívül, a csoport több más tagja, Pintér Ákos, Hajdu Lajos, Bérczes Attila is használták a Wiles-féle modularitási megközelítést, pl. az

$\displaystyle Ax^n-By^n=z^n $

egyenletcsaládra, ahol $ AB=2^\alpha q^\beta$, $ q=3,5,7,11,13$.

Tóth Árpád

ELTE, TTK Matematikai Intézet

Irodalomjegyzék

1. http://www.abelprize.no/nyheter/vis.html?tid=67106

2. Bashmakova, Isabella G., and Joseph H. Silverman. Diophantus and Diophantine equations. No. 20. Cambridge University Press, 1997.

3. Heath, Thomas Little, and Leonhard Euler. Diophantus of Alexandria: A study in the history of Greek algebra. CUP Archive, 1964.

 

4. Hellegouarch, Yves. Invitation to the mathematics of Fermat-Wiles. Academic Press, 2001.

 

5. Koblitz, Neal. “Elliptic curve cryptosystems.” Mathematics of computation 48.177 (1987): 203-209.

6. Liptai, Kriptográfia. http://www.tankonyvtar.hu/hu/tartalom/tamop425/0038_matematika_Liptai_Kalman-Kriptografia/ch10s06.html#id538428

7. NSA. The case for Elliptic Curve Cryptography https://web.archive.org/web/20090117023500/http://www.nsa.gov/business/programs/elliptic_curve.shtml

8. Rónyai Lajos. Fermat utolsó tétele http://db.komal.hu/KomalHU/cikk.phtml?id=199401

9. Simon Singh: A nagy Fermat-sejtés (Park Könyvkiadó, Budapest, 1998

10. Stopple, Jeffrey. A primer of analytic number theory: from Pythagoras to Riemann. Cambridge University Press, 2003.

11. http://mta.hu/kozgyules2017/akademiai-elismereseket-adtak-at-az-mta-188-kozgyulesen-107676

 

Lábjegyzetek

1 Itt Diofantosz a jelölésrendszer hiányosságai miatt, tetszőleges többszörös helyett egy konkrét számot, 2-t, választ.

2 Ez mutatja, hogy Diofantosz nem hagyományosan gondolkodott, hiszen a megjelenő mennyiségeknek más dimenziójuk van, így egyenlőségük geometriailag értelmezhetlen.