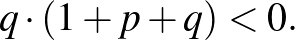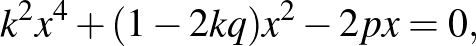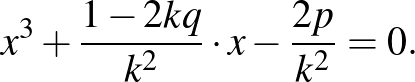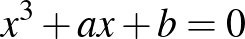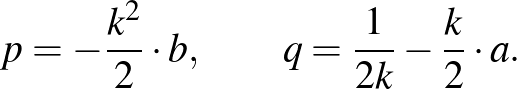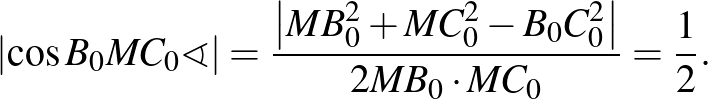Bevezetés
Éppen 130 éve, hogy Arany Dániel győri főreáliskolai tanár szerkesztésében először megjelent a Középiskolai Matematikai Lapok, vagy ahogy ma gyakran hívjuk, a KöMaL.
A folyóirat nagy szerepet töltött be a matematikai tehetségek felismerése és gondozása terén azzal, hogy izgalmas és érdekes problémákat tűzött ki, pontversenyt indított a feladatok megoldására és ezzel felkeltette, táplálta a matematika iránt fogékony, tehetséges tanulókban a versenyszellemet. A KöMaL ezt a szerepet minden bizonnyal ma is betölti.
Jelen írásnak nem célja a KöMaL történetének ismertetése vagy elemzése, az tanulmányozható például a felhasznált irodalomban szereplő [1] internetes oldalon is.
Meg kell említeni azonban a KöMaL történetének egy fontos dátumát, 1993-at, amikor is a 100 éves jubileum alkalmából megjelent egy dupla CD. Ez a két CD a KöMaL 1893-tól 1993-ig megjelent teljes anyagát tartalmazta ([2]).
A Bolyai János Matematikai Társulat 2022-ben Egerben rendezte a matematikát oktató tanítók és tanárok 61. Rátz László Vándorgyűlését. Ezen a vándorgyűlésen szerencsém és alkalmam volt a középiskolai szekcióban feladatmegoldó szemináriumot tartani.
Somfai Zsuzsa ( ) ötletének megfelelően a „Nagyjaink KöMaL-megoldásai a múltban” címet adtam ennek a szemináriumnak. A szeminárium alapjául az szolgált, hogy a két CD tanulmányozása során egyrészt nagyon sok szép feladatot találtam, másrészt a megoldók között olyan nevekkel találkoztam, akiknek a középiskolás évek után a választott pályája a matematika lett, és abban az igazán nagyok közé emelkedtek.
) ötletének megfelelően a „Nagyjaink KöMaL-megoldásai a múltban” címet adtam ennek a szemináriumnak. A szeminárium alapjául az szolgált, hogy a két CD tanulmányozása során egyrészt nagyon sok szép feladatot találtam, másrészt a megoldók között olyan nevekkel találkoztam, akiknek a középiskolás évek után a választott pályája a matematika lett, és abban az igazán nagyok közé emelkedtek.
Horváth Eszter, az Érintő Rátz Tanár Úr Életműdíjas szerkesztője vetette föl, hogy erről érdemes volna egy cikkben is megemlékezni. Így született meg az a gondolat, hogy 1900-tól 2000-ig a KöMaL csodálatos kincsestárából 10 évenként kiválasztok egy-egy feladatot, mégpedig olyanokat, amelyek megoldói pályájuk során híres matematikusok lettek.
Szép és izgalmas munka volt ez, különösen azért, mert 1900 és 2000 között minden évben találhattam ennek a feltételnek megfelelő feladatot és megoldókat.
A KöMaL 100 évének 10 feladata
Az alább következő tíz feladatot a Bevezetésben említett szempont alapján a KöMaL-ban 1900 és 2000 között megjelent sok-sok szép feladat közül válogattam, lényegében a bőség zavarával küszködve. Minden esetben ragaszkodtam a feladat eredeti szövegéhez. Az egyes feladatokhoz a versenyzők arcképét is mellékeltük. A képek legnagyobb része a KöMaL-archívum arcképcsarnokából származik, ahol ilyet nem sikerült találni, ott más internetes oldalról származó, nem diákkori képek kerültek beillesztésre.
Jelen válogatás nyilván nem mutathatja be, hogy a két időpont között eltelt 100 évben hogyan változott a KöMaL, milyen típusú és nehézségű feladatokat tűzött ki az éppen aktuális szerkesztőség. Csupán arra szeretnék kísérletet tenni a feladatokon és azok megoldásán keresztül, hogy érzékeltessem a nyilvánvalót, a KöMaL fontos szerepét a magyar matematikai tehetségek felismerésében és fejlődésében, a magyar matematika történetében.
A feladat után zárójelben szerepel a feladat szerzőjének neve (ahol az ismert), a megoldás közlésének éve és hónapja, a feladat sorszáma, végül pedig a feladat megoldóinak neve.
1. Legyenek 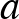 ,
, 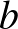 ,
, 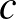 ,
,  és
és 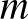 oly egész számok, hogy
oly egész számok, hogy
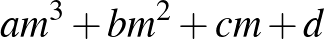
osztható 5-tel, de  nem osztható 5-tel. Bebizonyítandó, hogy ekkor mindig található oly
nem osztható 5-tel. Bebizonyítandó, hogy ekkor mindig található oly 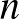 egész szám, hogy
egész szám, hogy
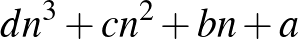
szintén osztható 5-tel.
(A Mathematikai és Phys. Társulat VII. tanulóversenyének tétele, 1901/2, 873., Kőnig Dénes, Haar Alfréd, Riesz Marcell)


2. Ha az 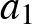 ,
, 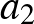 ,
, 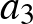 ,
,  ,
, 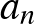 számok között vannak egymástól különbözők, akkor mutassuk meg, hogy
számok között vannak egymástól különbözők, akkor mutassuk meg, hogy
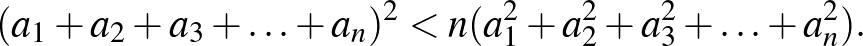
(1911/6, 2029., Szegő Gábor)
3. Szerkesztendő a kör, mely 3 adott egyenesen egyenlő szeleteket vág ki.
(1925/9, 38., Hajós György, Klein Eszter)


4. Bizonyítsuk be, hogy ha az
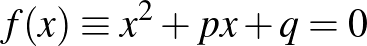
egyenletnek egyik gyöke 0 és 1 között van, akkor a
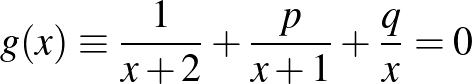
egyenletnek egy és csakis egy pozitív gyöke van.
(Vitéz Berend Iván tanár, Szeged, 1930/1, 526., Erdős Pál)
5. Egy halom pénz közt egy súlyban különbözik a többitől. Mennyi a legkevesebb mérés, amivel egy egyenlőkarú mérlegen eldönthetjük, hogy a rossz pénz könnyebb-e, vagy nehezebb a többinél?
(Kővári Tamás, Bp.-i ev.gimn.,VIII.o., 1948/9, 143., Fried Ervin, Gehér László)


6. Szerkesszünk  háromszöget, ha adva van a körülírt kör sugara
háromszöget, ha adva van a körülírt kör sugara 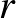 , továbbá az
, továbbá az 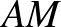 és
és 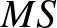 szakaszok hossza, ahol
szakaszok hossza, ahol  és
és 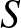 a háromszög magasság-, ill. súlypontja.
a háromszög magasság-, ill. súlypontja.
(Papp Éva, Bp., VIII., Ságvári lg., 1958/1, Győry Kálmán)
7. Adott az 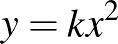 parabola. Határozzuk meg az
parabola. Határozzuk meg az 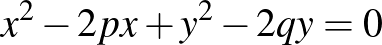 kör középpontját úgy, hogy az adott parabolával való metszéspontjainak abszcisszái az
kör középpontját úgy, hogy az adott parabolával való metszéspontjainak abszcisszái az 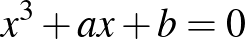 egyenlet gyökeit adják.
egyenlet gyökeit adják.
(Elemente der Mathematik, 1966/4, 1388., Recski András, Elekes György, Surányi László)

8. Adott egy különböző oldalú háromszög. Húzzuk meg egyik csúcsából a belső és külső szögfelezőt a szemben fekvő oldal egyeneséig és írjunk kört a végpontok közti szakasz mint átmérő fölé. Ismételjük meg szerkesztésünket egy másik csúcsból kiindulva és bizonyítsuk be, hogy a két körhöz a közös pontjukban húzott érintők közti hegyes szög 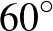 .
.
(1970/11, 1686., Frankl Péter, Komornik Vilmos)

9. A számegyenesen színezzük pirosra azokat a számokat, amelyek előállnak 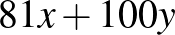 alakban, ahol
alakban, ahol 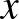 és
és 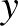 pozitív egészek, a többi egész számot pedig színezzük kékre. Bizonyítsuk be, hogy van olyan szám, hogy az erre szimmetrikusan elhelyezkedő számok színe különböző.
pozitív egészek, a többi egész számot pedig színezzük kékre. Bizonyítsuk be, hogy van olyan szám, hogy az erre szimmetrikusan elhelyezkedő számok színe különböző.
(1984/1, 2127. Bóna Miklós, Hraskó András, Kós Géza, Megyesi Gábor)


10. Egy paralelepipedonba beírt tetraéder lapsíkjai a paralelepipedonból négy tetraédert metszenek le. A paralelepipedon térfogatának hányad része annak a tetraédernek a térfogata, amelynek csúcsai a levágott tetraéderek súlypontjai?
(Fitos László, Esztergom, 1992/10, 2901., Csörnyei Marianna)
A feladatok megoldásai
A feladatok megoldásaiban is ragaszkodtam a KöMaL-ban közölt eredeti megoldáshoz, annak szövegéhez, a geometriai feladatok esetében az eredeti ábrához is. Csak ahhoz a feladathoz készítettem saját ábrát, amelyikhez a megoldás közlésekor nem tartozott. Mindezeknek a célja nyilván az volt, hogy ne csak egy-egy szép feladatról, hanem a megoldók egyedi ötleteiről, ismereteiről, széles látóköréről, végső soron magukról a megoldók személyéről is szóljunk. Az érdeklődő olvasó persze megpróbálkozhat egy-egy feladatnak az eredetihez képest eltérő, más ötleten alapuló, más eszközöket használó megoldásával.
Egy-egy feladat után az eredeti közlésben szereplő megjegyzéseket is leírtam, néhol saját megjegyzést fűztem hozzá.
1. Legyenek 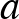 ,
, 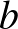 ,
, 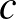 ,
,  és
és 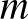 oly egész számok, hogy
oly egész számok, hogy
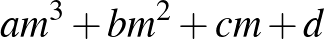
osztható 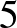 -tel, de
-tel, de  nem osztható
nem osztható 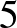 -tel. Bebizonyítandó, hogy ekkor mindig található oly
-tel. Bebizonyítandó, hogy ekkor mindig található oly 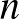 egész szám, hogy
egész szám, hogy
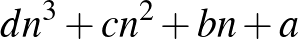
szintén osztható 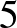 -tel.
-tel.
Megoldás. Minthogy 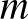 nem osztható 5-tel (ha ugyanis osztható volna, akkor az
nem osztható 5-tel (ha ugyanis osztható volna, akkor az 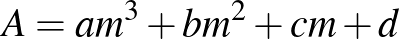 kifejezés csak úgy lenne osztható 5-tel, ha
kifejezés csak úgy lenne osztható 5-tel, ha  is osztható volna vele, de ez a feltétel szerint nem lehetséges), ezért
is osztható volna vele, de ez a feltétel szerint nem lehetséges), ezért 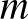 csakis
csakis

alakú lehet, ahol 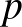 egész szám. Ha most
egész szám. Ha most 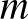 ezen értékeit helyettesítjük az
ezen értékeit helyettesítjük az 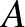 kifejezésbe és az 5-tel osztható tagokat elhagyjuk, akkor a következő kifejezéseket nyerjük:
kifejezésbe és az 5-tel osztható tagokat elhagyjuk, akkor a következő kifejezéseket nyerjük:
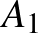 |
 |
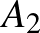 |
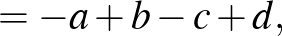 |
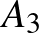 |
 |
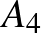 |
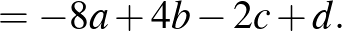 |
Most már bebizonyítandó, hogy ha ezen kifejezések bármelyike osztható 5-tel, akkor található oly 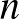 szám, hogy
szám, hogy 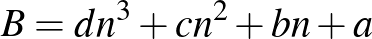 is osztható 5-tel, vagyis
is osztható 5-tel, vagyis 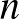 helyébe is hasonlóan, mint előbb az
helyébe is hasonlóan, mint előbb az 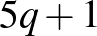 ;
; 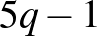 ;
; 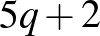 ;
; 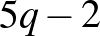 ;
;  értékeket helyettesítve
értékeket helyettesítve
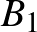 |
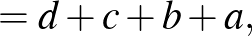 |
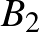 |
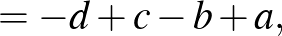 |
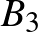 |
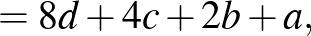 |
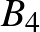 |
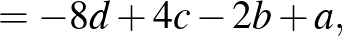 |
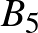 |
 |
kifejezések egyike is osztható.
Vegyük sorra az eseteket. Ha 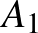 osztható, akkor a vele egyenlő
osztható, akkor a vele egyenlő  , ha pedig
, ha pedig 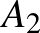 , akkor negatív értéke:
, akkor negatív értéke:  osztható. Továbbá, minthogy
osztható. Továbbá, minthogy 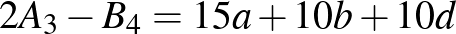 és
és 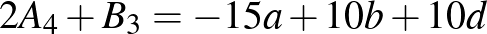 oszthatók 5-tel, ezért látjuk, hogy ha
oszthatók 5-tel, ezért látjuk, hogy ha 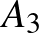 osztható
osztható 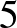 -tel, akkor
-tel, akkor  , ha pedig
, ha pedig 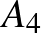 , akkor
, akkor 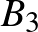 is osztható.
is osztható.
Bármily értéket teszünk is tehát 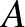 -ban
-ban 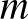 helyébe, hogy
helyébe, hogy 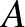 osztható legyen
osztható legyen 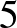 -tel, mindig találtunk olyan
-tel, mindig találtunk olyan 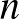 -t, hogy
-t, hogy 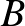 is
is 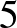 többszöröse lett.
többszöröse lett.
2. Ha az 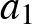 ,
, 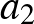 ,
, 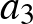 ,
,  ,
, 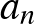 számok között vannak egymástól különbözők, akkor mutassuk meg, hogy
számok között vannak egymástól különbözők, akkor mutassuk meg, hogy
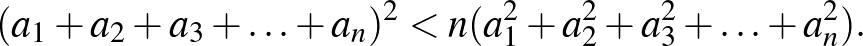
Megoldás. Ha az adott számok között vannak különbözők, akkor nem minden 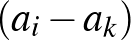 különbség értéke 0, tehát
különbség értéke 0, tehát
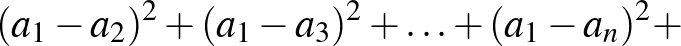 |
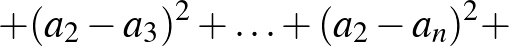 |
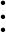 |
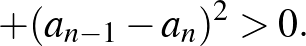 |
Mivel bármily 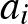 szám
szám 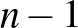 tagban fordul elő, azért a műveleteket végrehajtva ezt kapjuk:
tagban fordul elő, azért a műveleteket végrehajtva ezt kapjuk:
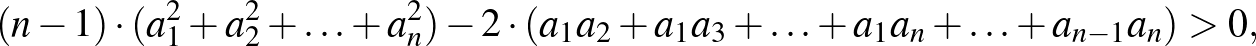
azaz
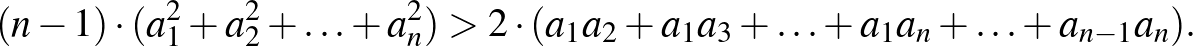
Adjuk az egyenlőtlenség mindkét oldalához az
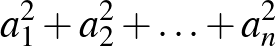
összeget, akkor
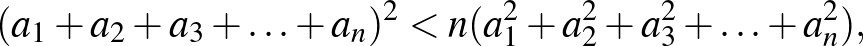
és éppen ezt akartuk bizonyítani.
3. Szerkesztendő a kör, mely 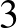 adott egyenesen egyenlő szeleteket vág ki.
adott egyenesen egyenlő szeleteket vág ki.
Megoldás. Az egyenesekből kivágott szeletek a kör húrjai; egyenlő húrok a kör középpontjától egyenlő távolságra vannak. Tehát oly pontot kell keresnünk, amely mindhárom egyenestől egyenlő távolságban van; ilyen pont, ha a három egyenes (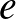 ,
, 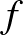 ,
, 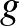 ) közül kettő-kettő metszi egymást,
) közül kettő-kettő metszi egymást, 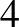 van, tudniillik az egyenesek metszéspontjaiként előálló
van, tudniillik az egyenesek metszéspontjaiként előálló  háromszöget belülről érintő kör és a három kívülről érintő kör középpontja. Ha ezen pontokból oly köröket rajzolunk, melyek rádiuszai nagyobbak, mint a beírt, illetve kívülről érintő (hozzáírt) körök sugarai, akkor ezek egyenlő szeleteket vágnak ki a három egyenesből.
háromszöget belülről érintő kör és a három kívülről érintő kör középpontja. Ha ezen pontokból oly köröket rajzolunk, melyek rádiuszai nagyobbak, mint a beírt, illetve kívülről érintő (hozzáírt) körök sugarai, akkor ezek egyenlő szeleteket vágnak ki a három egyenesből.
Ha a három egyenes közül kettő párhuzamos (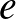 és
és 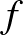 ), akkor az
), akkor az 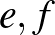 egyenesek
egyenesek 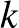 középpárhuzamosán két olyan pont lesz (
középpárhuzamosán két olyan pont lesz (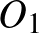 ,
, 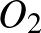 ), amely a kívánt tulajdonsággal rendelkező körök középpontja. Ezt a két esetet láthatjuk az alábbi ábrán.
), amely a kívánt tulajdonsággal rendelkező körök középpontja. Ezt a két esetet láthatjuk az alábbi ábrán.
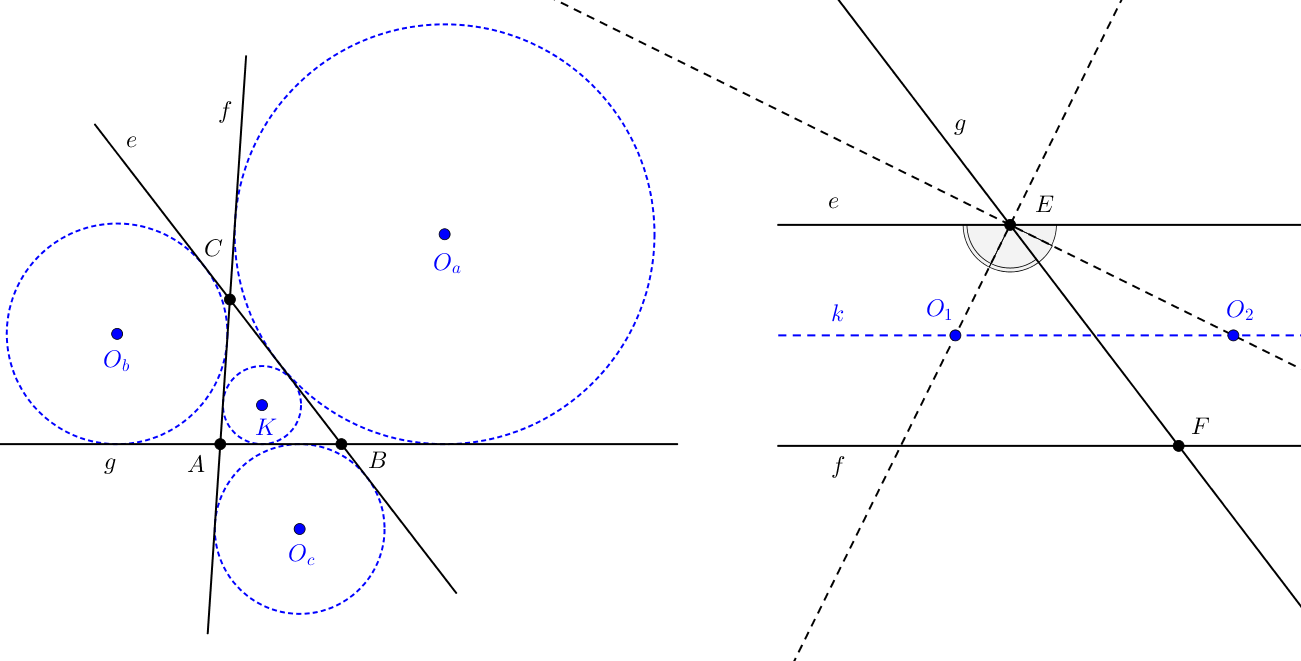
Ha mindhárom egyenes párhuzamos, akkor a feladat nem oldható meg (a keresett kör középpontja a végtelenben van).
Végül, ha a három egyenes egy pontban metszi egymást, ez a pont egyszersmind a keresett körök középpontja (minden szelet egyenlő az átmérővel).
4. Bizonyítsuk be, hogy ha az
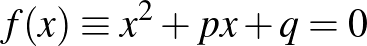
egyenletnek egyik gyöke 0 és 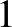 között van, akkor a
között van, akkor a
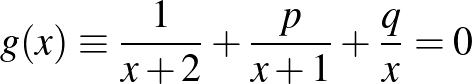
egyenletnek egy és csakis egy pozitív gyöke van.
Megoldás. Ha az 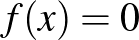 egyenletnek egyik gyöke 0 és 1 között van, akkor
egyenletnek egyik gyöke 0 és 1 között van, akkor  és
és 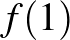 ellenkező előjelűek:
ellenkező előjelűek:
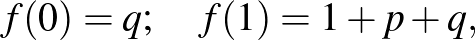
tehát
A 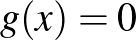 egyenlet gyökeit megadja az
egyenlet gyökeit megadja az
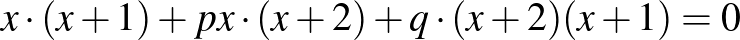
egyenlet, melyet rendezve:
A (2) egyenlet gyökeinek szorzata:
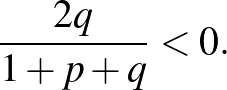
mert (1) szerint 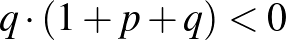 .
.
Ebből következik, hogy a (2) egyenlet gyökei valósak, és ellenkező előjelűek, tehát a 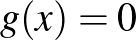 egyenletnek egy és csakis egy pozitív gyöke van.
egyenletnek egy és csakis egy pozitív gyöke van.
5. Egy halom pénz közt egy súlyban különbözik a többitől. Mennyi a legkevesebb mérés, amivel egy egyenlőkarú mérlegen eldönthetjük, hogy a rossz pénz könnyebb-e, vagy nehezebb a többinél?
Megoldás. Osszuk a pénzeket három csoportba. Az egyikben a felénél kevesebb pénzdarab legyen, a másik kettőben egyenlő számú.
a) Tegyük mérlegre az utolsó két csoportot. Egyensúly esetén a harmadik csoportban van a hamis, tehát azt, ugyanannyi jónak bizonyult pénzdarabbal mérve meg, megkapjuk a választ kérdésünkre.
b) Ha a mérleg félrebillen, akkor vegyük pl. a nehezebb csoportot, tegyünk hozzá a félretett (tehát jónak bizonyult) pénzdarabok közül úgy, hogy összesen páros számú pénzdarab legyen és tegyük a két felét a mérlegre.
Egyensúly esetén a másik részben van, tehát könnyebb a rossz pénz a jóknál, ha pedig ismét megbillen a mérleg, akkor nehezebb a többinél.
A módszer csak 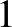 és
és 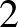 darab pénznél nem használható, de akkor nem is eldönthető a kérdés.
darab pénznél nem használható, de akkor nem is eldönthető a kérdés.
6. Szerkesszünk  háromszöget, ha adva van a körülírt kör sugara
háromszöget, ha adva van a körülírt kör sugara 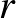 , továbbá az
, továbbá az 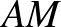 és
és 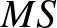 szakaszok hossza, ahol
szakaszok hossza, ahol  és
és 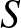 a háromszög magasság-, ill. súlypontja.
a háromszög magasság-, ill. súlypontja.
Megoldás. A háromszög Feuerbach-körének tulajdonságait fogjuk felhasználni a szerkesztéshez.
Ismeretes, hogy az  magasságpont, a Feuerbach-kör
magasságpont, a Feuerbach-kör 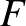 középpontja és az
középpontja és az 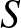 súlypont egy egyenesen vannak, mégpedig úgy, hogy
súlypont egy egyenesen vannak, mégpedig úgy, hogy
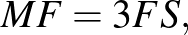
azonkívül a Feuerbach-kör sugara a körülírt kör sugarának a fele. A Feuerbach-kör átmegy a magasságok talppontjain és az 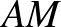 távolság
távolság 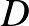 felezőpontján (2. ábra).
felezőpontján (2. ábra).
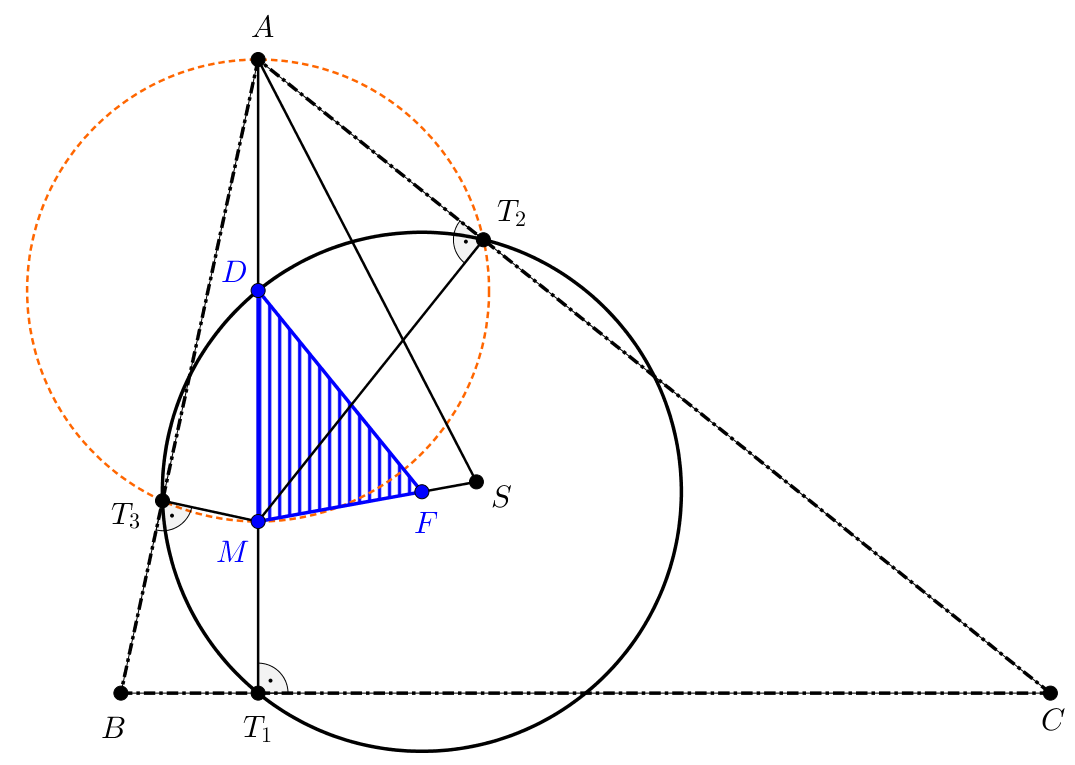
Ilyenformán az 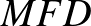 háromszög szerkeszthető: oldalai ismertek. A háromszög megszerkesztése után megrajzoljuk az
háromszög szerkeszthető: oldalai ismertek. A háromszög megszerkesztése után megrajzoljuk az 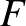 középpontú,
középpontú, 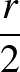 sugarú Feuerbach-kört. Az
sugarú Feuerbach-kört. Az 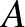 csúcsot megkapjuk, ha
csúcsot megkapjuk, ha  -et tükrözzük
-et tükrözzük 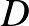 -re. Az
-re. Az 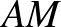 egyenesnek a Feuerbach-körrel való másik metszéspontja az
egyenesnek a Feuerbach-körrel való másik metszéspontja az 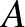 -ból húzott magasság talppontja, az erre a
-ból húzott magasság talppontja, az erre a 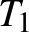 pontban állított merőleges a
pontban állított merőleges a 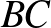 oldal irányát adja.
oldal irányát adja.
Az 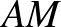 fölé rajzolt Thales-kör kimetszi a Feuerbach-féle körből a másik két magasságtalppontot, s az
fölé rajzolt Thales-kör kimetszi a Feuerbach-féle körből a másik két magasságtalppontot, s az 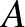 pontot a
pontot a 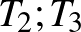 pontokkal összekötve megkapjuk a
pontokkal összekötve megkapjuk a  és
és 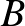 pontokat.
pontokat.
Van megoldása a feladatnak, ha egyrészt az 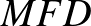 háromszög szerkeszthető, másrészt pedig, ha a
háromszög szerkeszthető, másrészt pedig, ha a 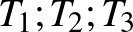 talppontok léteznek.
talppontok léteznek.
Megjegyzések.
1. A feladatra a KöMaL 1958/1 száma több megoldást is közölt.
A fenti (a nyomtatott számban a II.) megoldásba egy apró nyomdai hiba került bele, éspedig a helyes 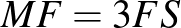 összefüggés
összefüggés 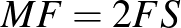 alakban jelent meg. Ez azonban a megoldás menetét nem befolyásolta.
alakban jelent meg. Ez azonban a megoldás menetét nem befolyásolta.
2. Egyik megoldás sem említette a feladat megoldhatóságát abból a szempontból, hogy az  háromszög hegyesszögű, tompaszögű vagy derékszögű.
háromszög hegyesszögű, tompaszögű vagy derékszögű.
7. Adott az 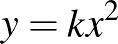 parabola. Határozzuk meg az
parabola. Határozzuk meg az 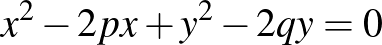 kör középpontját úgy, hogy az adott parabolával való metszéspontjainak abszcisszái az
kör középpontját úgy, hogy az adott parabolával való metszéspontjainak abszcisszái az 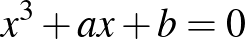 egyenlet gyökeit adják.
egyenlet gyökeit adják.
Megoldás. Az előírt kör 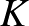 középpontjának koordinátái
középpontjának koordinátái  . Ezek ismerete elegendő a kör megrajzolásához, mert a körnek át kell mennie az
. Ezek ismerete elegendő a kör megrajzolásához, mert a körnek át kell mennie az 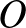 origón, hiszen az
origón, hiszen az  értékpár kielégíti az egyenletet.
értékpár kielégíti az egyenletet.
A parabolának és a körnek legfeljebb 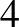 közös pontja lehet. Ugyanis a két egyenletből
közös pontja lehet. Ugyanis a két egyenletből 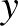 -t kiküszöbölve
-t kiküszöbölve 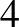 -edfokú egyenletet kapunk:
-edfokú egyenletet kapunk:
így legfeljebb 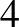 valós szám szerepelhet közös pont abszcisszájaként, és a parabolának minden abszcisszán csak egy pontja van. Egy közös pontjuk az origó, további közös pontjaik abszcisszái azt az egyenletet elégítik ki, amelyet (3)-ból az ismert
valós szám szerepelhet közös pont abszcisszájaként, és a parabolának minden abszcisszán csak egy pontja van. Egy közös pontjuk az origó, további közös pontjaik abszcisszái azt az egyenletet elégítik ki, amelyet (3)-ból az ismert 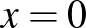 gyökhöz tartozó
gyökhöz tartozó  gyöktényező leválasztásával kapunk:
gyöktényező leválasztásával kapunk:

Itt 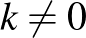 – különben parabola helyett az
– különben parabola helyett az 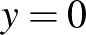 egyenessel állnánk szemben –, ezért az egyenlet ekvivalens az alábbival:
egyenessel állnánk szemben –, ezért az egyenlet ekvivalens az alábbival:
A parabolának és a körnek az origótól különböző metszéspontjaihoz tartozó abszcisszák adják meg az
egyenlet gyökeit – azaz minden valós gyökét –, ha (4) ekvivalens (5)-tel, vagyis ha további két együtthatójuk rendre egyenlő:
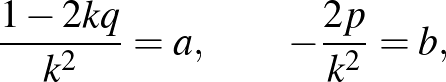
és innen
Ezek szerint az (5) egyenlet gyökeit leolvashatjuk mint az adott 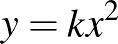 parabola és a (6) kifejezésekkel meghatározott
parabola és a (6) kifejezésekkel meghatározott  középpontú,
középpontú,  sugarú kör közös pontjainak abszcisszáit. Pl.
sugarú kör közös pontjainak abszcisszáit. Pl. 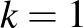 -et választva a
-et választva a
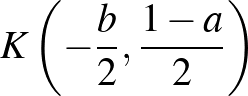
középpont körüli, az  -n átmenő körrel kell metszenünk a normálparabolát.
-n átmenő körrel kell metszenünk a normálparabolát.
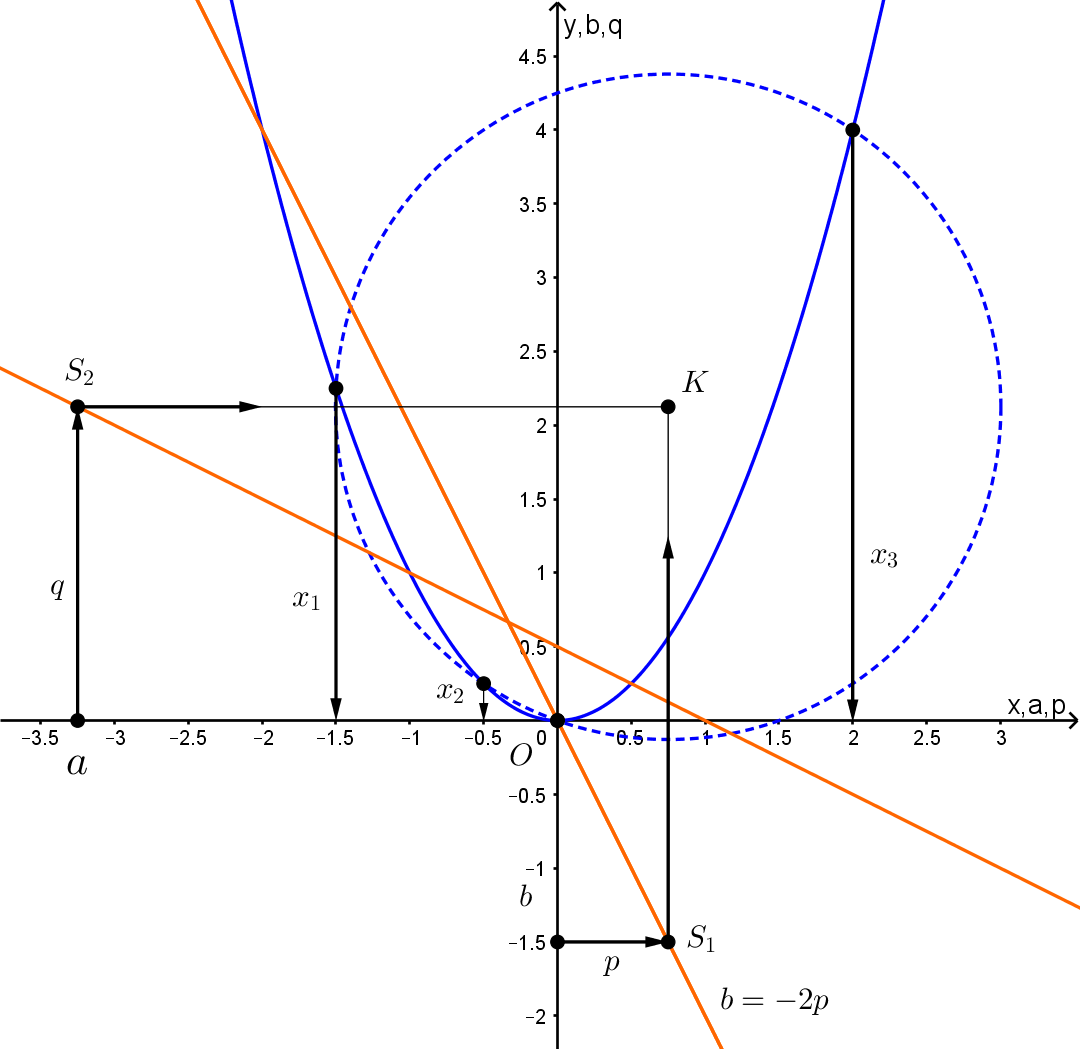
A 3. ábrán a 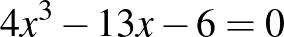 egyenlet megoldása látható, itt
egyenlet megoldása látható, itt  ,
, 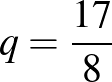 , továbbá
, továbbá 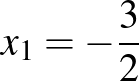 ,
, 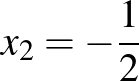 és
és 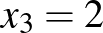 .
.
Megjegyzés. Kézenfekvő, hogy a harmadfokú egyenlet grafikus megoldásában a  koordinátákat is grafikusan állítsuk elő. Erre valók (továbbra is
koordinátákat is grafikusan állítsuk elő. Erre valók (továbbra is 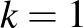 esetében) az ábra segédegyenesei, melyeknek egyenlete:
esetében) az ábra segédegyenesei, melyeknek egyenlete:

Az elsőnek 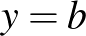 ordinátájú
ordinátájú  pontjához
pontjához 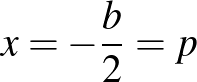 abszcissza tartozik, tehát
abszcissza tartozik, tehát  az
az  segédponton átmenő, az
segédponton átmenő, az 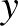 -tengellyel párhuzamos egyenesen lesz. A második segédegyenes
-tengellyel párhuzamos egyenesen lesz. A második segédegyenes 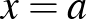 abszcisszájú
abszcisszájú 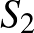 pontjához tartozó ordináta
pontjához tartozó ordináta 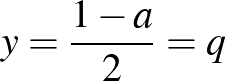 , tehát
, tehát 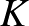 -t a legutóbbi egyenesből az
-t a legutóbbi egyenesből az 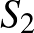 -n átmenő, az
-n átmenő, az 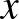 -tengellyel párhuzamos egyenes metszi ki.
-tengellyel párhuzamos egyenes metszi ki.
8. Adott egy különböző oldalú háromszög. Húzzuk meg egyik csúcsából a belső és külső szögfelezőt a szemben fekvő oldal egyeneséig és írjunk kört a végpontok közti szakasz mint átmérő fölé. Ismételjük meg szerkesztésünket egy másik csúcsból kiindulva és bizonyítsuk be, hogy a két körhöz a közös pontjukban húzott érintők közti hegyes szög 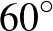 .
.
Megoldás. Válasszuk úgy az  háromszög betűzését, hogy a szokásos jelölésekkel
háromszög betűzését, hogy a szokásos jelölésekkel 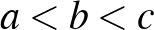 teljesüljön. Az állítást a
teljesüljön. Az állítást a  és
és  csúcsokból kiindulva kapott körökre bizonyítjuk, ennek mintájára végezhető a bizonyítás a további két körpár esetére is.
csúcsokból kiindulva kapott körökre bizonyítjuk, ennek mintájára végezhető a bizonyítás a további két körpár esetére is.
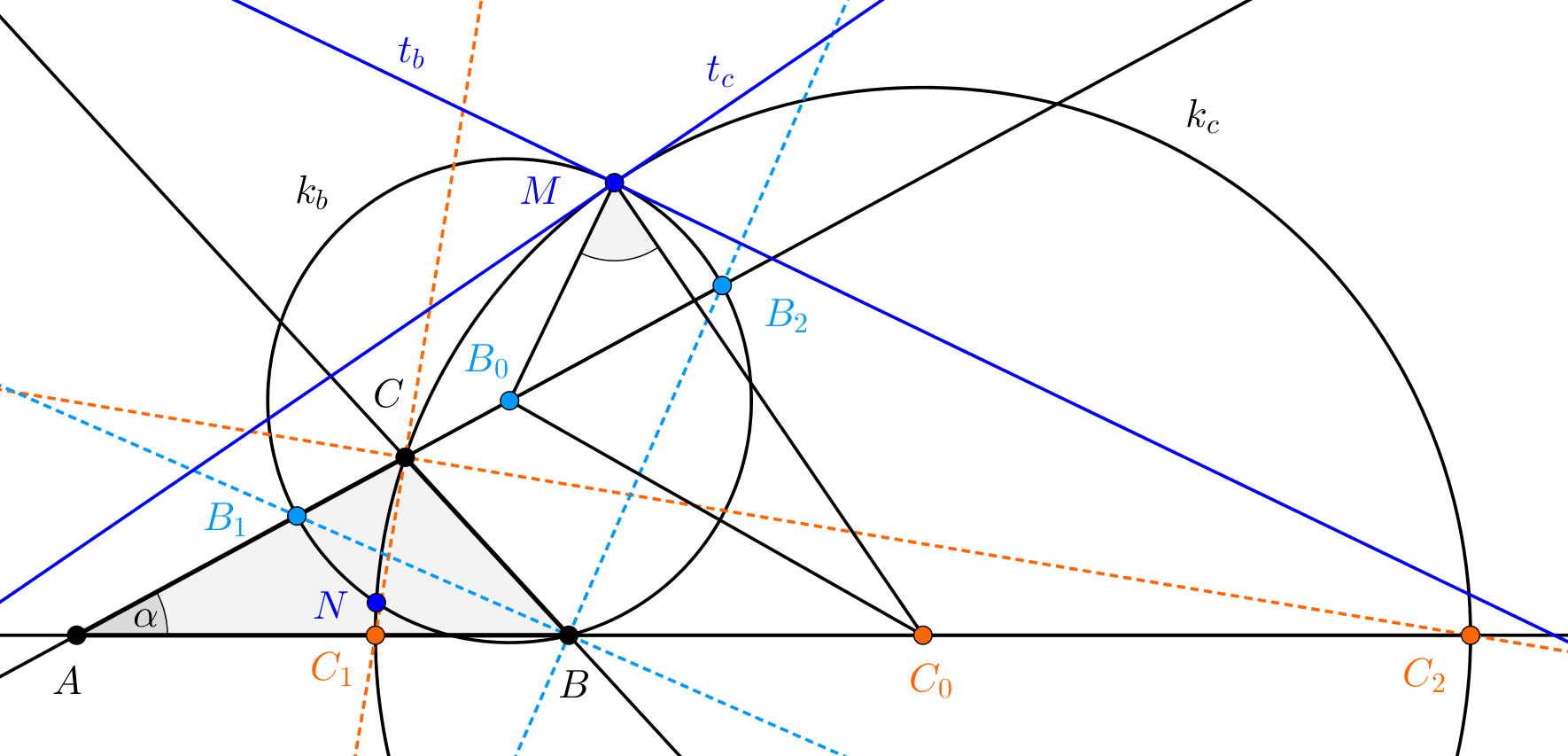
Legyen a  -ből induló belső és külső szögfelezőnek az
-ből induló belső és külső szögfelezőnek az  egyenessel való metszéspontja
egyenessel való metszéspontja 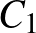 , illetve
, illetve  , a
, a 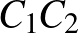 szakasz fölötti
szakasz fölötti  Thalész-kör középpontja
Thalész-kör középpontja 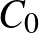 , a
, a 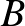 -ből kiindulva ugyanígy kapott pontok és kör rendre
-ből kiindulva ugyanígy kapott pontok és kör rendre 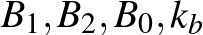 , végül
, végül 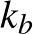 és
és  egyik metszéspontja
egyik metszéspontja  .
.
A körök  -beli
-beli 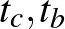 érintőit
érintőit  körül
körül 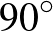 -kal elforgatva a megfelelő sugarak
-kal elforgatva a megfelelő sugarak 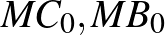 egyenesét kapjuk, így elegendő azt belátni, hogy
egyenesét kapjuk, így elegendő azt belátni, hogy  értéke
értéke 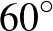 vagy
vagy 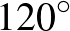 , azaz, hogy
, azaz, hogy
Az 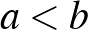 feltétel miatt
feltétel miatt 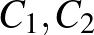 az
az 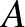 -nak ugyanazon oldalán vannak, mint
-nak ugyanazon oldalán vannak, mint 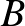 és így
és így 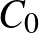 is ezen az oldalon van, ennélfogva a szögfelezők osztásarányának tétele alapján
is ezen az oldalon van, ennélfogva a szögfelezők osztásarányának tétele alapján
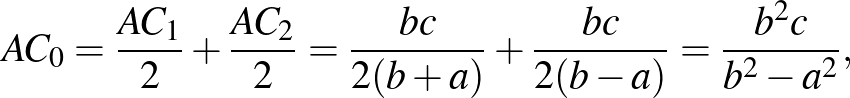
és ugyanezekkel a szakaszokkal
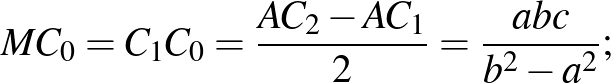
továbbá hasonlóan
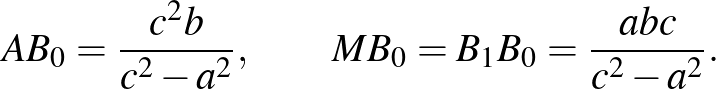
Ezekkel a (7)-beli számláló, a koszinusztételt az 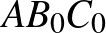 és az
és az  háromszögre alkalmazva:
háromszögre alkalmazva:
 |
 |
tehát (7) valóban fennáll. Ezt akartuk bizonyítani.
Megjegyzés.
A fentiekhez hasonlóan igazolható, hogy a két kör másik metszéspontjában, tehát a 4. ábra 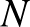 pontjában is
pontjában is 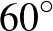 -ot zárnak be az érintők.
-ot zárnak be az érintők.
9. A számegyenesen színezzük pirosra azokat a számokat, amelyek előállnak 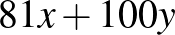 alakban, ahol
alakban, ahol 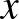 és
és 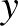 pozitív egészek, a többi egész számot pedig színezzük kékre. Bizonyítsuk be, hogy van olyan szám, hogy az erre szimmetrikusan elhelyezkedő számok színe különböző.
pozitív egészek, a többi egész számot pedig színezzük kékre. Bizonyítsuk be, hogy van olyan szám, hogy az erre szimmetrikusan elhelyezkedő számok színe különböző.
Megoldás. A legkisebb piros szám nyilván a 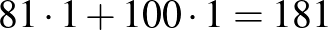 .
.
Megmutatjuk, hogy 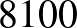 kék. Ha ugyanis
kék. Ha ugyanis 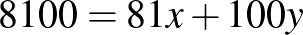 volna, ahol
volna, ahol 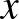 és
és 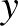 pozitív egészek, akkor
pozitív egészek, akkor 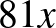 osztható volna
osztható volna 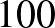 -zal. Mivel
-zal. Mivel 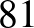 -nek és
-nek és 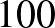 -nak nincs
-nak nincs 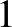 -nél nagyobb közös osztója, ezért
-nél nagyobb közös osztója, ezért 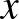 is osztható volna
is osztható volna 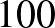 -zal, vagyis
-zal, vagyis 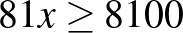 lenne. Ekkor viszont
lenne. Ekkor viszont 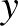 nem lehet pozitív.
nem lehet pozitív.
Belátjuk, hogy 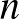 és
és  közül az egyik piros, a másik kék. Ez egyúttal a feladat állítását is adja, hiszen ez éppen azt jelenti, hogy a
közül az egyik piros, a másik kék. Ez egyúttal a feladat állítását is adja, hiszen ez éppen azt jelenti, hogy a 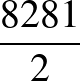 -re szimmetrikusan elhelyezkedő számok különböző színűek.
-re szimmetrikusan elhelyezkedő számok különböző színűek.
Először is nem lehet 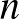 és
és  egyaránt piros. Ha mégis így volna, akkor pozitív egész
egyaránt piros. Ha mégis így volna, akkor pozitív egész  -vel
-vel
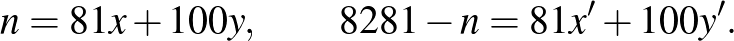
Ezeket összeadva kapjuk, hogy
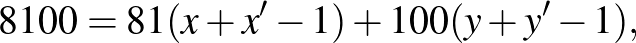
és itt 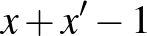 , valamint
, valamint 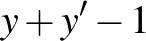 pozitív egészek. Így
pozitív egészek. Így 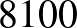 piros lenne, noha láttuk, hogy kék.
piros lenne, noha láttuk, hogy kék.
Így tehát 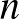 és
és  közül legalább az egyik kék.
közül legalább az egyik kék.
Másodszor megmutatjuk, hogy ha 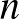 kék, akkor
kék, akkor  piros, azaz e két szám közül legfeljebb az egyik lehet kék.
piros, azaz e két szám közül legfeljebb az egyik lehet kék.
Mivel  , azért
, azért
Válasszuk meg a 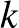 egész számot úgy, hogy
egész számot úgy, hogy
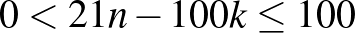
legyen, ekkor az 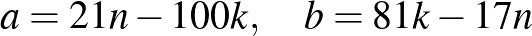 kifejezéseket (8)-ba írva
kifejezéseket (8)-ba írva
Itt 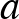 pozitív egész,
pozitív egész, 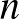 pedig kék, tehát
pedig kék, tehát 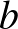 nem lehet pozitív, vagyis
nem lehet pozitív, vagyis 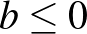 .
.
A (9) összefüggésből
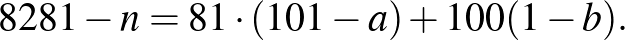
Ebben az előállításban 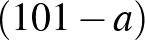 és
és 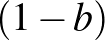 is pozitív egész, ezért
is pozitív egész, ezért 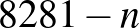 piros.
piros.
Így 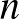 és
és  legalább és legfeljebb az egyik, vagyis pontosan az egyik kék, a másik piros.
legalább és legfeljebb az egyik, vagyis pontosan az egyik kék, a másik piros.
Tehát 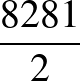 az állításnak megfelelő szám.
az állításnak megfelelő szám.
Megjegyzések.
1. A feladat szoros kapcsolatban áll az 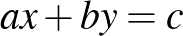 alakú, úgynevezett diofantikus egyenletek vizsgálatával. Ebben az egyenletben
alakú, úgynevezett diofantikus egyenletek vizsgálatával. Ebben az egyenletben 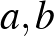 és
és 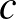 egészek, és a megoldásokat is az egész számok között keressük. Könnyen igazolható, hogy ennek az egyenletnek akkor és csak akkor van megoldása, ha
egészek, és a megoldásokat is az egész számok között keressük. Könnyen igazolható, hogy ennek az egyenletnek akkor és csak akkor van megoldása, ha 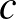 többszöröse
többszöröse 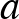 és
és 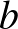 legnagyobb közös osztójának.
legnagyobb közös osztójának.
2. Ha 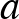 és
és 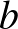 pozitív egészek, továbbá
pozitív egészek, továbbá 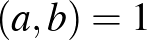 , akkor az
, akkor az 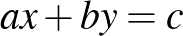 egyenlet
egyenlet  -re a pozitív számok körében mindig megoldható. Másfelől az
-re a pozitív számok körében mindig megoldható. Másfelől az 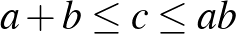 esetekben az
esetekben az ![$[a+b,ab]$](/images/stories/latexuj/2023-06/2023-06-100ev10komalfeladat/img203.png) intervallum felezőpontjára szimmetrikusan elhelyezkedő számok közül pontosan az egyikre oldható meg az egyenlet.
intervallum felezőpontjára szimmetrikusan elhelyezkedő számok közül pontosan az egyikre oldható meg az egyenlet.
10. Egy paralelepipedonba írt tetraéder lapsíkjai a paralelepipedonból négy tetraédert metszenek le. A paralelepipedon térfogatának hányad része annak a tetraédernek a térfogata, amelynek csúcsai a levágott tetraéderek súlypontjai?
Megoldás. Használjuk az 5. ábra jelöléseit.
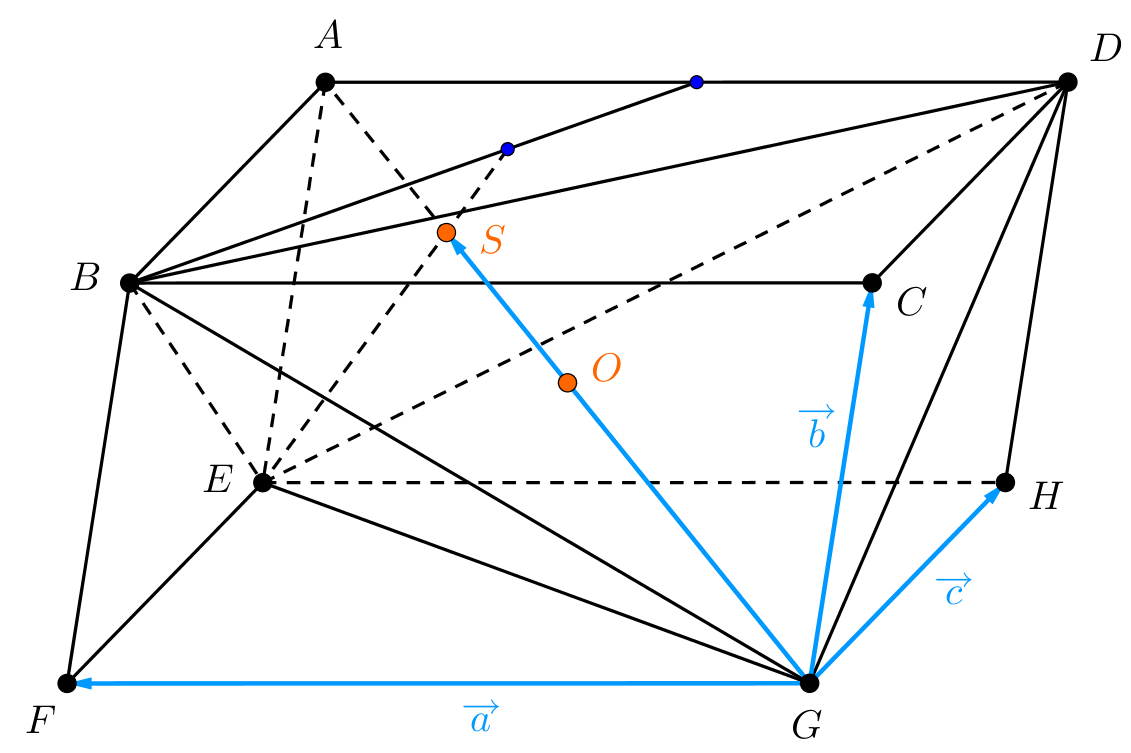
Ismeretes, hogy minden paralelepipedonba két tetraédert lehet írni, amelyek a paralelepipedon  középpontjára tükrösek, és bármelyiknek a térfogata a paralelepipedonénak
középpontjára tükrösek, és bármelyiknek a térfogata a paralelepipedonénak  -ad része.
-ad része.
Látni fogjuk, hogy a feladat megoldása szempontjából mindegy, hogy melyik tetraédert választjuk.
Az ábrán a 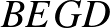 tetraédert rajzoltuk meg. Belátjuk, hogy ennek a térfogata a a paralelepipedonénak
tetraédert rajzoltuk meg. Belátjuk, hogy ennek a térfogata a a paralelepipedonénak  -a.
-a.
Mivel pl. az 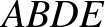 levágott tetraéder
levágott tetraéder  lapjának területe a paralelepipedon
lapjának területe a paralelepipedon 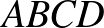 lapja területének a fele, az ezekhez a lapokhoz tartozó magasság pedig ugyanaz, ezért egy levágott tetraéder térfogata a paralelepipedon térfogatának
lapja területének a fele, az ezekhez a lapokhoz tartozó magasság pedig ugyanaz, ezért egy levágott tetraéder térfogata a paralelepipedon térfogatának  -od része. A négy levágott tetraéder térfogatának összege
-od része. A négy levágott tetraéder térfogatának összege 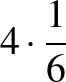 rész, így a beírt tetraéder köbtartalma valóban
rész, így a beírt tetraéder köbtartalma valóban  -a a paralelepipedon térfogatának.
-a a paralelepipedon térfogatának.
Legyen az 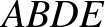 tetraéder súlypontja
tetraéder súlypontja 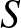 . Írjuk föl a
. Írjuk föl a 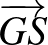 vektort. Tekintve, hogy
vektort. Tekintve, hogy  ,
,  ,
,  és
és 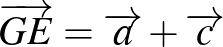 , az
, az 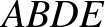 tetraéder súlypontjának helyvektora így kapható meg:
tetraéder súlypontjának helyvektora így kapható meg:
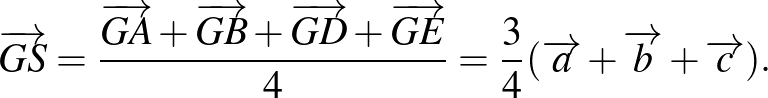
Ezért

Ebből láthatjuk, hogy 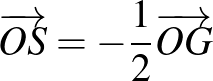 , ami azt jelenti, hogy az
, ami azt jelenti, hogy az 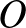 centrumú,
centrumú, 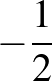 arányú középpontos hasonlóságban
arányú középpontos hasonlóságban 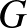 képe
képe 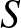 .
.
Ugyanígy a másik három levágott tetraéder súlypontja a beírt tetraéder egy-egy további csúcsának képe az említett középpontos hasonlóságban. Ezért a súlypontok meghatározta tetraéder térfogata a beírt tetraéder térfogatának 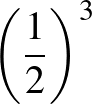 -szerese, tehát a paralelepipedon köbtartalmának
-szerese, tehát a paralelepipedon köbtartalmának 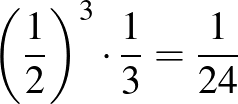 része.
része.
Megjegyzések.
1. Néhány megoldó elemi geometriai eszközökkel (paralelogramma tulajdonságok, súlyvonalak osztási aránya) találta meg az előzőekben leírt 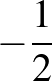 arányú középpontos hasonlóságot. Ezek az egyébként szép megoldások valamivel hosszabbak, mint a fenti vektoros megoldás.
arányú középpontos hasonlóságot. Ezek az egyébként szép megoldások valamivel hosszabbak, mint a fenti vektoros megoldás.
2. Csörnyei Marianna 2. megoldásában felhasználta, hogy a paralelepipedon affinitással kockába vihető át. Mivel az affinitás aránytartó, elegendő a feladatot kockára megoldani. Ezután kiszámította a súlypontok által meghatározott (szabályos) tetraéder élét, majd a térfogatát.
A feladatok megoldóiról
A fenti tíz feladat megoldói a KöMaL pontversenyén, a különféle országos versenyeken, a Nemzetközi Matematikai Diákolimpián olyan sok szép eredményt értek el, hogy ennek teljes felsorolására jelen írás terjedelmi okokból nem vállalkozhat. Ezért ebben a fejezetben a feladatok megoldóinak matematikusi pályáját szeretnénk röviden ismertetni.
1. feladat
Kőnig Dénes (1884–1944): Matematikus, egyetemi tanár, Kőnig Gyula matematikus fia. Matematikusként a gráfelmélet világhírű úttörője és kutatója. Első gráfelméleti munkája a Középiskolai Matematikai Lapok 1926 májusi számában jelent meg A graphokról címmel. Nevét viseli például a gráfelméletben Kőnig-tételként ismert fontos eredmény.
Haar Alfréd (1885–1933): Matematikus, egyetemi tanár, a Magyar Tudományos Akadémia tagja. Kutatási területei közé tartoztak az ortogonális függvénysorok, a parciális differenciálegyenletek, a többváltozós variációproblémák, illetve a szinguláris integrálok. 1929-ben Hamburgban vendégtanárként mutatta be a variációszámításban elért eredményeit. Az invariáns csoportmértékek (Haar-mérték) létezésének bizonyításával a modern matematikai kutatások elindítója lett.
Riesz Marcell: (1886–1969): Matematikus, egyetemi tanár, Riesz Frigyes matematikus testvére. Kutatásai kezdetben a trigonometrikus sorok vizsgálatára irányultak, ezen a területen nemzetközi hírnevet szerzett. A trigonometrikus polinomokra vonatkozó interpolációs képlete ma is e tudományág standard anyagát képezi. Érdeklődése később a potenciálelmélet, a hullámterjedés és a kvantummechanika matematikai problémái felé fordult, ezeken a területeken érte el legfontosabb eredményeit.
2. feladat
Szegő Gábor (1895–1985): Matematikus, a Magyar Tudományos Akadémia tagja, több külföldi egyetem tanára volt. Legjelentősebb matematikai eredményeit a komplex függvénytan, a Fourier-sorok, a potenciálelmélet területén érte el, de nevéhez fűződik az ortogonális polinomok általános elméletének kidolgozása is.
3. feladat
Hajós György (1912–1972): Matematikus, egyetemi tanár, a Magyar Tudományos Akadémia tagja. Fontos eredményeket ért el a diszkrét geometria, a rácspont-geometria, a Bolyai–Lobacsevszkij-féle geometria, a geometriai szerkesztések elmélete, a gráfelmélet, a nomográfia, és a numerikus analízis területén. Legjelentősebb, nemzetközi hírnevet is szerzett felfedezése Minkowskinak egy, az 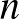 dimenziós tér egységkockákkal történő rácsszerű lefedésével kapcsolatos sejtésének bizonyítása volt. Egyetemi tanárként sok tankönyvet, jegyzetet írt, egyik alapvető egyetemi tankönyve a Bevezetés a geometriába című, ezt az egyetemeken ma is használják.
dimenziós tér egységkockákkal történő rácsszerű lefedésével kapcsolatos sejtésének bizonyítása volt. Egyetemi tanárként sok tankönyvet, jegyzetet írt, egyik alapvető egyetemi tankönyve a Bevezetés a geometriába című, ezt az egyetemeken ma is használják.
Klein Eszter (1910–2005): Matematikus. Már budapesti gimnazistaként is a matematika iránt érdeklődőket tömörítő Anonymus-csoport tagja volt, Erdős Pállal, Turán Pállal, Szekeres Györggyel együtt. Klein Eszter nevéhez fűződik a ma Happy End-problémaként ismert kombinatorikus geometriai feladat felvetése és első megoldása: bárhogyan veszünk fel a síkban öt általános helyzetű pontot, mindig kiválasztható belőlük egy konvex négyszög négy csúcsa. Ez ma a kombinatorikus geometria egyik alapvető eredménye. A problémát Erdős Pál és Szekeres György később közös dolgozatban általánosította. Klein Eszter és Szekeres György 1937-ben összeházasodtak (innen a probléma elnevezése), később Ausztráliában telepedtek le, életük végéig tanítottak Adelaide és Sydney egyetemein.
4. feladat
Erdős Pál (1913–1996): A 20. század egyik legnagyobb matematikusa, a Magyar Tudományos Akadémia tagja, az Akadémia Matematikai Intézete külső tudományos főmunkatársa, számtalan külföldi egyetem doktora, a londoni székhelyű Royal Society tagja. Munkássága a halmazelméletben, a kombinatorikában és a számelmélet több területén alapvetően meghatározta a matematika fejlődésének irányait. Rényi Alfréddal a véletlen gráfok elméletének kidolgozója. Több matematikai tétel névadója, de sejtései is világhírűvé váltak, mint például az elsőként L.J. Mordell által bizonyított Erdős–Mordell-egyenlőtlenség. Ez a nevezetes első megoldás a KöMaL-ban jelent meg 1935-ben. Erdős Pál sok díj és elismerés birtokosa volt, 1984-ben Wolf-díjat kapott.
5. feladat
Fried Ervin (1929–2013): Matematikus, az ELTE Algebra és Számelmélet Tanszékének professzora. Fő kutatási területe az algebra volt. Publikációi mellett több, az egyetemeken ma is használatos algebra tankönyv szerzője volt, megjelentek a modern algebrát népszerűsítő könyvei, mint például az Absztrakt algebra elemi úton, de középiskolai tankönyet is írt a speciális matematika tagozatos osztályok számára Lineáris algebra címmel.
Gehér László (1929–2011): Matematikus, középiskolai tanár. Nyugdíjazásáig a Szegedi Tudományegyetem Geometria tanszékének oktatója, 2002-től egyetemi docense. Doktori dolgozatát Szőkefalvi-Nagy Béla vezetésével 1985-ben fejezte be. Több tudományos cikket is publikált, de főként kiváló egyetemi előadó, emellett középiskolásoknak tartott olimpiai előkészítő szakkörök vezetője volt. Munkáját a Bolyai János Matematikai Társulat Grünwald Géza Díjjal ismerte el.
6. feladat
Győry Kálmán (1940–): Széchenyi-díjas matematikus, egyetemi tanár, a Magyar Tudományos Akadémia tagja, a számelmélet nemzetközi hírű kutatója. Akadémiai disszertációjának címe: Diofantikus problémákra vonatkozó effektív végességi tételek és alkalmazásaik. Számtalan publikációja jelent meg magyar, angol és francia nyelven,  külföldi egyetem vendégprofesszora volt tudományos munkája során. Jelenleg is a a debreceni Számelméleti Kutatócsoport vezetője.
külföldi egyetem vendégprofesszora volt tudományos munkája során. Jelenleg is a a debreceni Számelméleti Kutatócsoport vezetője.
7. feladat
Recski András (1948–): Matematikus, a Budapesti Műszaki Egyetem tanszékvezető professzora. A Magyar Tudományos Akadémia Matematikai Bizottságának, Számítógéptudományi Bizottságának és Tudományetikai Bizottságának tagja, a Rényi Alfréd Matematikai Kutatóintézet külső tagja. Kutatási területe a diszkrét matematika, elsősorban a matroidelmélet és kombinatorikus optimalizáció, valamint ezek alkalmazásai a villamos hálózatok elméletében, a nagybonyolultságú integrált áramkörök tervezésében és a statikában, kutatásaival kapcsolatosan nagyszámú publikációt jelentetett meg. Emellett számos külföldi egyetemen vendégoktatóként dolgozott. A Bolyai János Matematikai Társulat elnökségi tagja volt.
Elekes György (1949–2008): Matematikus, 2001-től a Magyar Tudományos Akadémia doktora, 2005-től az ELTE egyetemi tanára, alapítója az ELTE Számítógéptudományi Tanszékének. Kutatási területei közé tartozott a kombinatorikus geometria, a számelmélet és a halmazelmélet. Erdős Pállal és Hajnal Andrással a kombinatorikus halmazelmélet egy új ágát fejlesztették ki. A geometriai algoritmusok területén alapvető eredmény kapcsolódik a nevéhez, amelyet angol nyelven A geometric inequality and the complexity of computing volume címmel publikált. Kiváló oktató volt, több egyetemi tankönyv szerzője.
Surányi László (1949–): Matematikus, 10 évig a Magyar Tudományos Akadémia Matematikai Kutatóintézetének munkatársa, majd középiskolai vezető tanár a Budapesti Fazekas Mihály Gimnáziumban. Kutatási területei közé tartozik a metaaxiomatika, a művészetek és a matematika kapcsolata. Számos angol és magyar nyelvű gráfelméleti publikáció szerzője illetve társszerzője, segédtankönyvet írt Algebra-testek, gyűrűk, polinomok címmel, tanulmányokat jelentetett meg Középiskolai Matematikai Lapokban, feladatgyűjtemények összeállításában vett részt. Szívesen publikál a matematika oktatásának általános kérdéseiről, rendszeres előadója a matematikatanárok Rátz László Vándorgyűlésének, de foglalkozik filozófiai kérdések széles körével is. Munkásságáért 2008-ban Rátz Tanár Úr Életműdíjban részesült.
8. feladat
Frankl Péter (1953–): Matematikus, a Tokioi egyetem tanára, a Magyar Tudományos Akadémia külső tagja. Kombinatorikával, illetve extremális hipergráf-problémákkal foglalkozik, ehhez a területhez jelentős eredményei fűződnek. A japán diákolimpiai csapat egyik felkészítője. Babai Lászlóval közösen írt egy könyvet a lineáris algebrai módszerek kombinatorikai alkalmazásáról. 1978-ban artistavizsgát tett.
Komornik Vilmos (1954–): Matematikus, a matematikai tudományok doktora, a Magyar Tudományos Akadémia külső tagja. Kutatási területei közé tartozik az analízis, a parciális differenciálegyenletek, a kontrollelmélet, és a kombinatorikus számelmélet. Publikációiban, szerzőként vagy társszerzőként írt könyveiben főként ezen területek problémáit elemzi.
9. feladat
Bóna Miklós (1967–): Az ELTE-n végzett matematikus szakon. Doktori dolgozatát az USA-ban a világhírű Massachusetts Institute of Technology intézetben készítette. Egy évet töltött Princetonban az Institute for Advanced Study tagjaként. A kombinatorika, ezen belül a permutációk elmélete, a számelmélet és a kommutatív algebra kutatója. 2010 óta az Electronic Journal of Combinatorics egyik főszerkesztője.
Hraskó András (1966–): Matematikus, 2006-ban az ELTE-n készítette doktori dolgozatát Geometriai tételek a harmadrendű görbe csoporttulajdonságával összefüggésben címmel. Dolgozott a speciális matematika tagozatos osztályok tanáraként a budapesti Fazekas Mihály Gimnáziumban, munkatársa volt az ELTE Matematikatanítási és Módszertani Központjának. Több, a matematikai tehetséggondozást segítő feladatgyűjtemény, interneten elérhető szakköri anyag [9] készítője, illetve a matematikát népszerűsítő kiadvány szerzője, vagy társszerzője: Bergengóc példatár, Új matematikai mozaik. Néhány éve a The London School of Mathematics and Programming munkatársa. 2000-ben a svájci Elemente der Mathematik folyóirat közölte egy angol nyelvű dolgozatát Poncelet-type Problems, an Elementary Approach címmel.
Kós Géza (1967–): Az ELTE matematikus szakán végzett 1991-ben. Az egyik kutatócsoportban a geometria informatikai kérdéseivel foglalkozott, az Informatika Karon ebből a témából szerezte meg doktori fokozatát 2002-ben. Több angol nyelvű tudományos dolgozat szerzője illetve társszerzője, az ELTE Analízis tanszékének adjunktusa. A Nemzetközi Matematikai Diákolimpia problémakiválasztó bizottságának tagja, a magyar diákolimpiai csapat egyik felkészítője, korábbi csapatvezetője. A KöMaL matematikai szerkesztőbizottságának tagja, internetes megjelenésének, az úgynevezett Munkafüzet-nek a felelőse illetve internetes fórumának létrehozója.
Megyesi Gábor (1966–): Egyetemi matematikai tanulmányait Szegeden kezdte, később a cambridge-i Trinity College ösztöndíjas hallgatója lett. Doktori fokozatát is itt szerezte. Vendégoktatója volt a Max Planck Intézetnek (Németország) és az Utah Egyetemnek (USA). Jelenleg a Manchesteri Egyetem tanára, ahol kombinatorikát, gráfelméletet, matematikai kommunikációt és algebrai geometriát tanít. Kutatóként a szinguláris felületekre vonatkozó egyenlőtlenségek általánosításával foglalkozik.
10. feladat
Csörnyei Marianna (1975–): Matematikus szakon végzett az ELTE-n 1999-ben, ugyanebben az évben PhD fokozatot szerzett. Egy tanévet a Princeton Egyetemen töltött az Institute for Advanced Study kutatójaként. Jelenleg a Chicagói Egyetem professzora. A London Mathematical Society folyóiratainak szerkesztője. A Magyar Tudományos Akadémiának 2019-től külső tagja. A valós analízis, a geometriai mértékelmélet és a geometriai nemlineáris funkcionálanalízis kutatója, ezeken a területeken nemzetközileg elismert eredményekkel rendelkezik.
Összegzés
Nyilvánvaló, hogy a fenti írás nem adhatott teljes áttekintést a KöMaL 100 évéről. Ugyanakkor remélhető, hogy a kiválasztott feladatok önmagukban is érdekesek voltak, és a megoldási módjukban megnyilvánuló ötletek, módszerek tanulságul szolgáltak.
A KöMaL szerkesztőségi tagjaként (és a pontverseny valamikori résztvevőjeként) úgy vélem, hogy a feladatok rendszeres beküldése az egyik legjobb feladat-és problémamegoldó iskola. Ezt akartam érzékeltetni a feladatok egykori megoldóinak matematikusi pályáját ismertetve (ha mégoly röviden is).
Az írás tehát valójában a KöMaL pontversenyein való, az eddiginél is szélesebb körű és eredményesebb részvételre szeretne ösztönözni.
Felhasznált irodalom
- [1] http://db.komal.hu/KomalHU/tortenet.phtml
- [2] KöMaL-CD 1893.-1993.(szkennelt oldalak)
- [3] http://db.komal.hu/KomalHU/ (KöMaL-archívum)
- [4] https://www.nevpont.hu/foglalkozasok/matematikus
- [5] https://www.arcanum.com/hu/adt/
- [6] https://edu.ek.szte.hu/szegedi-tudosok-a-halozatban/a-szegedi-matematikai-iskola/kislexikon/
- [7] https://math.unideb.hu/hu/oneletrajz
- [8] https://m2.mtmt.hu/gui2/
- [9] https://matek.fazekas.hu/
Bíró Bálint