Bevezető
Tapasztalataink szerint sokan elvesztegetett időnek tartják a matematikaórák játékkal töltött perceit. Ám vannak, akik – velünk együtt – lehetőséget látnak a játékokban. 2019-ben, a Varga Tamás Módszertani Napokon mutatta be például Antal Zoltán az érdeklődőknek, kollégáknak, fiataloknak, ő hogyan alkalmazza a játékokat a matematikatanításban. Előadása és az ehhez kapcsolódó játékos foglalkozás sokunkat megfogott.
2010-ben, a Varga Tamás Tanítványainak Emlékalapítvány támogatásával, Pálfalvi Józsefné és Oláh Vera szervezésében indult el egy pályázat keretében a „Játéktól a kutatásig” program évi 3 alkalommal matematikai és természettudományi témájú ingyenes foglalkozásokkal.
A pályázat lejárta után, 2013-tól kezdve a program csökkentett – elsősorban matematikai – tartalommal az évente megrendezett Varga Tamás Napok keretében élt tovább Pálfalvi Józsefné szervezésében és szakmai irányításával. A szerzők rendszeres szervezési munkája mellett több jeles oktató is közreműködött, sőt, tanár szakos hallgatóinkat is bevontunk a foglalkozások szervezésébe, levezetésébe, az ötletek kidolgozásába.
A programok során igyekeztünk olyan játékokat, játékos feladatokat bemutatni, amelyek alkalmasak az érdeklődés felkeltésére, matematikai tanulsággal bírnak és továbbgondolásra is érdemesek. Követtük azt az elvet, amelyeket a felfedeztető matematikatanítás, valamint a Varga Tamás vezette matematika kísérlet is fontosnak tart: a matematikai játékok alkalmazása a gondolkodás „nem verbális” (háttérben történő) fejlesztése.
Az iskolai tanítás során is színesebbé, érdekesebbé tehetjük óráinkat egy-egy játék vagy játékos feladat beillesztésével. Ehhez felhasználhatjuk már ismert játékok, rejtvénytípusok vagy televíziós és interneten könnyen szerkeszthető vetélkedők alapötletét (pl. dominó, memory, puzzle, Libajáték, Ne nevess korán, kincskeresés, akadályverseny, kártyajátékok stb.) a matematikai tartalomnak megfelelően elkészített eszközökkel. Idesoroljuk az egyre inkább elérhető informatikai eszközöket is; a vetélkedőt például valamely telefonos applikáció segítségével szervezhetjük meg. Az alkalmasan megválasztott játékok az érdeklődés felkeltése, kedvcsinálás mellett alkalmasak lehetnek gondolkodási módszerek (pl. indukció, analógia, invariánsok) felismertetésére, felfedeztetésére, bemutatására, szemléltetésére, tudatosítására, alkalmazására és gyakorlására. Felfedeztethetünk, bevezethetünk, gyakorolhatunk új fogalmakat, fejleszthetjük a matematikai kompetenciákat. A játék egy áttekinthető szituációban, mindenki által ismert kifejezőeszközökkel zajlik, ahol a rámutatás, utánozás, elmozdítás stb. megengedett és így épít a nem verbális elemekre is.
A játék során a tanár, a „játékvezető” csak szervező, irányító, a kipróbálás során nem avatkozik bele a játékba. Ilyenkor lehetősége van arra, hogy megfigyelje, miként alakítják ki a gyerekek a stratégiáikat saját és egymás gondolataira alapozva. Érdemes a gyerekeket arra bíztatni, hogy maguk is alkossanak szabályokat, új játékokat.
Az itt következő játékok egy része a „Játéktól a kutatásig” vagy valamelyik Varga Tamás Módszertani Napok diákprogramjában szerepelt. A felhasznált ötletek részben Pósa Lajostól származnak, mások közismert játékokból.
Őszintén reméljük, hogy cikkünkkel ezúton is felkeltjük Olvasóink érdeklődését és figyelmét a játékos foglalkozások mellett a Varga Tamás Módszertani Napokra is, amely egyedülálló módon ingyenes, színvonalas előadásokat és workshopokat kínáló, tanároknak, hallgatóknak és diákoknak szóló konferencia. Sok szeretettel várjuk kollégáinkat, az érdeklődőket és diákjaikat a minden év november 3-adika és 9-edike közé eső pénteki és szombati napon megrendezendő konferenciára. Külön kiemeljük, hogy a diákok számára olyan élmény lehet a játékos programon való részvétel, amelyet az iskolai órákon nincs lehetőségük megélni, így rájuk különösen számítunk.
(Tájékozódni – és a korábbi konferenciák anyagát megtekinteni – a http://mathdid.elte.hu/html/vtn.html honlapon lehet. Játékaink – és sok más játék és matematikai háttérrel rendelkező, különböző életkorú és képzettségű tanulók oktatásában felhasználható ötlet – szintén megtalálhatók a mathdid.elte.hu honlapon, az „Elemi matematika tanároknak” című elektronikus jegyzetben.)
Számlétra és variációi
1. Számlétra
1.1. Ketten játszanak egymás ellen, „Első” és „Második”. Első mond egy 1 és 10 közötti számot (beleértve a határokat). Második ehhez hozzáad egy 1 és 10 közötti számot, és közli az eredményt. Ezek után mindig az aktuális eredményhez adnak hozzá felváltva egy 1 és 10 közötti számot. Az nyer, aki végül kimondja a 100-at. Kinek van „nyerő stratégiája”? Kinek van esélye a nyerésre? Hogyan játsszon?
Stratégia. Könnyű rájönni, hogy aki 89-et mond, az megnyerheti a játékot (az ellenfél erre nem tud 100-at mondani, de akármit mond, utána a soron következő tud). Új cél tehát a 89. Ezt (hasonló alapon) akkor tudjuk elérni, ha előtte 78-at tudunk mondani. Így folytatva, ha nyerni akarunk, nekünk kell mondanunk a 67, 56, 45, 34, 23, 12, 1 számokat, vagyis Első tud nyerni, ha 1-gyel kezd (és jól játszik). Kezdő stratégiáját úgy is megfogalmazhatjuk, hogy első lépésre 1-et mond, ezután az ellenfél lépését mindig kiegészíti 11-re.
A játék szervezése. Érdemes tanulói párokban kipróbálni a játékot. Aki már úgy gondolja, hogy van nyerő stratégiája, az játszhat a tanár ellen úgy, hogy megválaszthatja, hogy Első vagy Második akar-e lenni. Tanárként nem érdemes kezdettől „jól játszani”, mert könnyű ellesni a „jó számokat” azoknak is, akik nem találták meg a nyerő stratégiát. „Rossz játékkal” ellenőrizhetjük, hogy tényleg megfejtette-e a diák a dolog nyitját.
Ellenőrizhetjük, hogy a megbeszélt stratégiát ki értette meg, ha újra játsszuk a játékot 100 helyett más végső számmal, és/vagy más lépéshosszokkal.
A játékot úgy is játszhatjuk, hogy egy sorban megszámozott mezőkből álló pályán (esetleg a számegyenesen) kell a játékosoknak egy bábuval felváltva lépniük.

Megjegyzések: A játék egyik elterjedt változatában (Fejben 21) a cél a 21 elérése, a „lépésköz” pedig 1, 2 vagy 3 lehet. Kisebb gyerekekkel, illetve egyéb módszertani meggondolások alapján kezdhetünk ezzel az egyszerűbb feladattal.
A játék során szerzett tapasztalatok segíthetnek a maradékosztályok mélyebb megértésében.
A Számlétrának nagyon sok variációját lehet megmutatni, ezek közül ismertetünk néhányat, amelyeket mi is szoktunk játszani.
1.2. Nem az nyer, aki kimondja a 100-at, hanem az veszít, aki kénytelen a 100-at kimondani (vagy átlépni).
Stratégia: Ha sikerül 99-et mondanunk, nyertünk. Innentől az eredeti játék, avval a változással, hogy cél a 99. Ilyenkor Második nyerhet.
Megjegyzés: Érdemes különböző célok vagy lépéshosszok esetén tisztázni, hogy mikor kinek van „nyerő stratégiája”, hiszen a nyerő-vesztő cél cseréje nem automatikusan jár együtt azzal, hogy a kezdő, vagy a másik nyerhet-e.
1.3. Az eredeti játék során egyszer lehet passzolni (a két játékosnak összesen egyszer, vagyis ha valamelyikük passzolt, akkor a másik már nem teheti ezt meg).
Stratégia: Mondjunk az alapjáték „jó számainál” eggyel kisebb számokat, amíg az ellenfél nem passzol. Ha az ellenfél mond egy, az eredetiben ilyen „jó” számot, akkor passzoljunk. A másodiknak van nyerő stratégiája.
Megjegyzés: Meggondolható, hogy mi a helyzet (összesen, tehát nem fejenként) két, három, ... megengedett passz esetén.
1.4. Számozott mezők esetén úgy is játszhatjuk a játékot, hogy Első az 1 előtt, Második a 100 (vagy az aktuális utolsó szám) mögött helyezi el a bábuját, visszafelé haladva indul, vagyis egymással szembe mennek. Egymást átugrani nem szabad, az veszít, aki nem tud lépni.
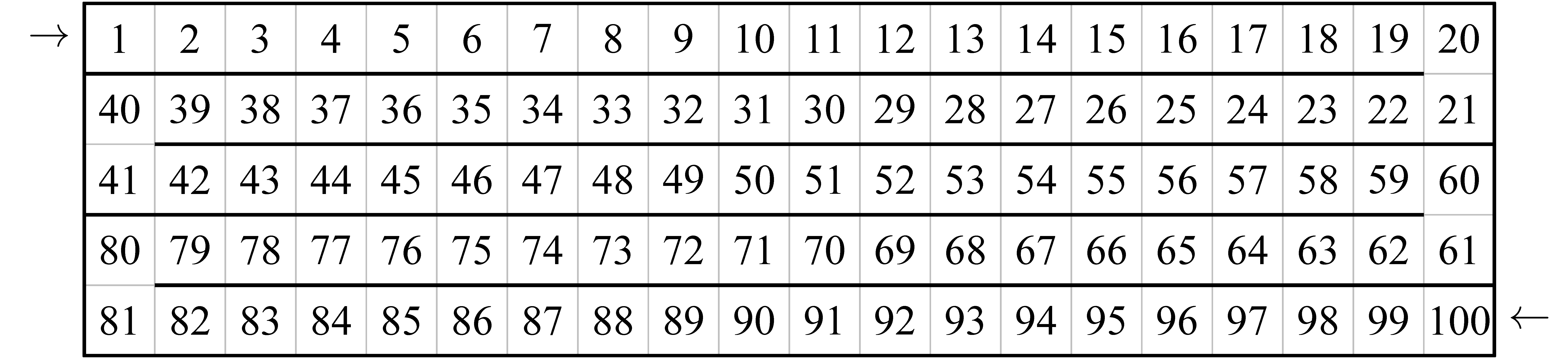
Stratégia: Ha úgy képzelnénk el az eredeti játékot, hogy „visszafelé” haladnak, 100-ból kell kivonniuk a játékosoknak felváltva 1 és 10 közötti számokat, akkor a cél a 0 lenne. Ha egymással szemben mennek, akkor a távolságukat szeretnék 1-re csökkenteni.
Érdekes megfigyelni, mikor veszik észre a gyerekek a kétféle játék közti szoros kapcsolatot.
1.5. Egy 10-szer 10-es négyzetrácson a jobb fölső mezőből akarunk eljutni a bal alsó mezőre balra vagy lefelé lépéssel úgy, hogy a lépés hossza 1 és 10 mező közé essen (beleértve a határokat), és a lépés közben egyszer megváltoztathatjuk az irányt. Az nyer, aki a bal alsó mezőre lép.
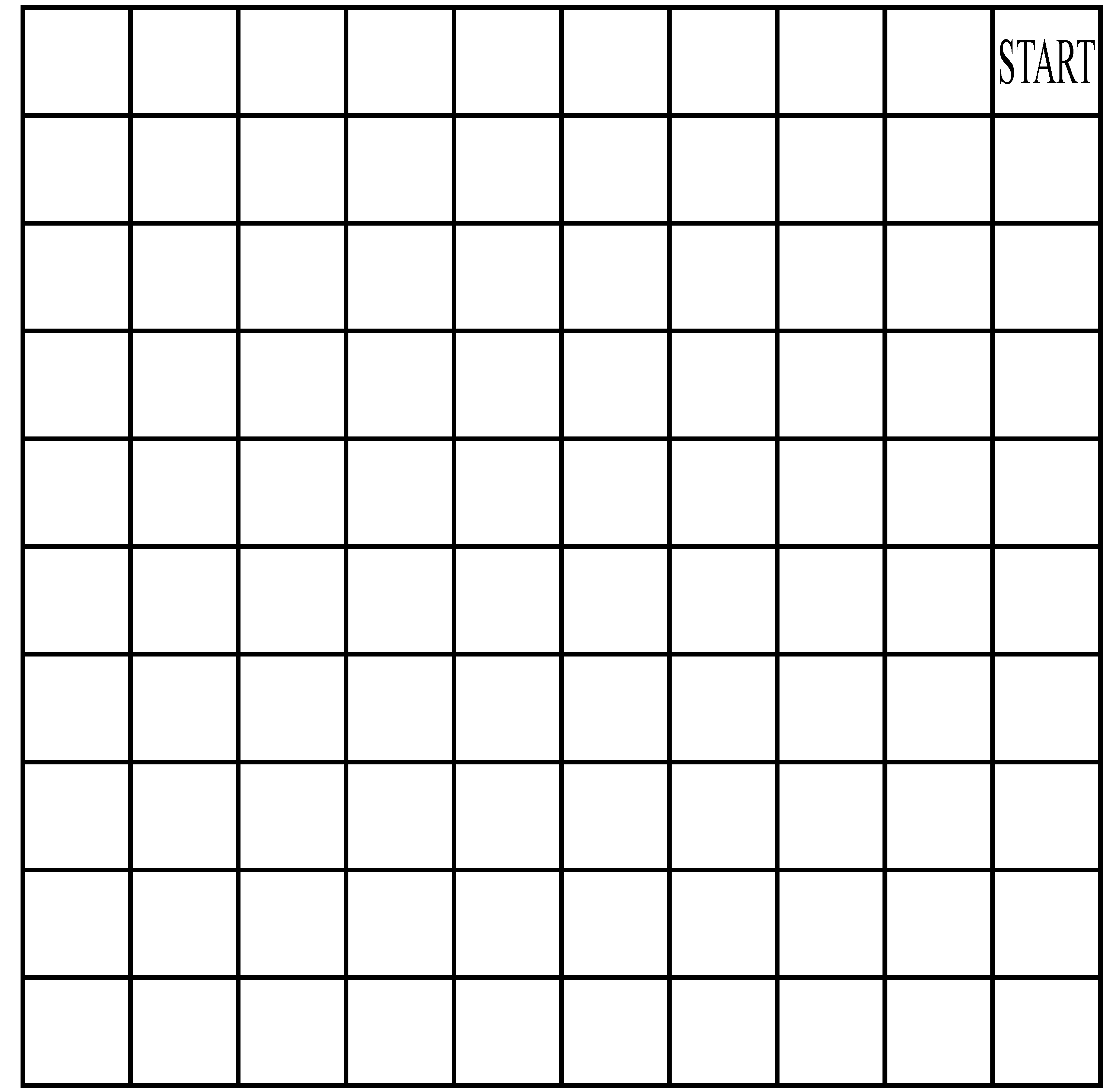
Stratégia: Jelöljük a mezőket két koordinátával. Az induló mező legyen a (0,0), az utolsó mező a 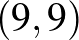 (a koordináták balra, illetve lefelé növekednek). Vegyük észre, hogy mindegy, hányszor váltunk irány a lépés során, egy-egy lépésben a kiindulási mezőhöz képest az érkezési mező koordinátái összege egy 1 és 10 közé eső számmal nő (beleértve 1-et és 10-et is). Az utolsó mező koordinátáinak összege 18, így ha olyan mezőre lép a kezdő, amelynek koordinátái összege eléri a 8-at, biztosan veszít. Ezért a kezdőnek olyan mezőn kell kezdenie, amelynek koordinátái összege legfeljebb 6. Második innen csak olyan mezőre léphet, amely koordinátái összege 7 és 17 közé esik, azaz Első innen egy lépésben eljuthat a
(a koordináták balra, illetve lefelé növekednek). Vegyük észre, hogy mindegy, hányszor váltunk irány a lépés során, egy-egy lépésben a kiindulási mezőhöz képest az érkezési mező koordinátái összege egy 1 és 10 közé eső számmal nő (beleértve 1-et és 10-et is). Az utolsó mező koordinátáinak összege 18, így ha olyan mezőre lép a kezdő, amelynek koordinátái összege eléri a 8-at, biztosan veszít. Ezért a kezdőnek olyan mezőn kell kezdenie, amelynek koordinátái összege legfeljebb 6. Második innen csak olyan mezőre léphet, amely koordinátái összege 7 és 17 közé esik, azaz Első innen egy lépésben eljuthat a 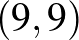 koordinátájú mezőre, és nyer.
koordinátájú mezőre, és nyer.
A számlétra játékot és a változatait más eszközökkel is lehet játszani, nem csak számokkal fejben vagy „számegyenesen”, hanem például kupacokban elhelyezett kavicsokkal.
2. Kavicskupacok
2.1. Egy 100 kavicsból álló kupacból 2 játékos felváltva vehet el 1 és 10 közötti darabszámú kavicsot. Az nyer, aki az utolsót elveszi.
Megjegyzés: Ez nyilván ugyanaz a játék, mint a számlétra, csak éppen visszafelé haladva. Jól látszik, hogy szembe haladás esetén ugyanezt a játékot kapjuk, hiszen mindegy, hogy a kavicskupac „melyik széléből” veszünk el kavicsokat.
2.2. Egy nehezebben megfejthető játék: Egy (legalább két kavicsból álló) kavicskupacból felváltva vesznek el a játékosok, a következő szabály szerint: Első elvehet akármennyit (legalább egyet), csak az összeset nem. A továbbiakban mindenki elvesz legalább egyet és legfeljebb kétszer annyit, mint előtte az ellenfele. Az nyer, aki az utolsó kavicsot elveszi.
Tapasztalatszerzés: Mivel ennek a játéknak a stratégiáját az eddigi játékokénál nehezebb megtalálni, érdemes kevés számú kaviccsal kezdeni. Feltételezzük, hogy mindkét játékos igyekszik nyerni, és ennek érdekében mindig a lehető legjobb lépést teszi meg.
Azt nem nehéz meggondolni, hogy 2, 3 kavics esetén Első veszít, mert akárhány kavicsot vesz is el (az összeset nem lehet), Második elveheti a maradékot.
Ha a kavicsok száma 4, akkor Első csak úgy nyerhet, ha 1-et vesz el, ekkor ugyanis Másodiknak 3 kavics marad, és – mint láttuk – abból akárhányat vesz is el, Első elveheti a maradékot.
Ebből az is látszik, hogy ha egy játékos 3 kavicsot hagy, akkor csak abban az esetben nyeri meg a játékot, ha előzőleg legfeljebb 1 kavicsot vett el – mert ekkor Második csak 1-et vagy 2-t tud elvenni –, vagyis ha előzőleg 4 kavics volt. Ebből az is következik, hogy 4 kavicsos kupaccal a kezdő tud nyerni.
4 kavics esetén a kezdő nyerhet.
Ha 5 kavics van, akkor amennyiben Első 1-et vesz el, Másodikat hozza nyerő helyzetbe az előző meggondolás szerint, míg ha 2-t vagy annál többet, akkor Második közvetlen nyerő lépést tehet.
5 kavics esetén a kezdő veszít.
Ezért 5 kavics mellett elérhető, hogy a soron következő veszítsen, de csak abban az esetben, ha az elvett kavicsok száma 1 vagy 2 (hogy ne tudja egyből elvenni az összes maradék kavicsot). Azaz 6 vagy 7 kavics esetén Első tud nyerni.
Ha 8 kavics van a kupacban: Első nyilván nem fog 3 vagy annál több kavicsot elvenni, mert akkor Második közvetlen nyer; ha viszont csak 1-et vagy 2-t vesz el, akkor is veszít, hiszen – mint láttuk – 6 vagy 7 kavics esetén a soron következő nyer.
8 kavics esetén a kezdő veszít.
Előbb-utóbb megsejthető, hogy ha kezdetben a kavicsok darabszáma Fibonacci-szám, akkor – mindkét játékos jó játéka esetén – Második nyerhet, minden más esetben Első tud nyerni.
Magyarázat: Indukcióval vázlatosan megmutatjuk, hogy Fibonacci-szám darabszámú kavicskupac esetén Második nyer, minden más esetben Első. (A Fibonacci-számokat 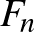 -nel jelöljük,
-nel jelöljük, 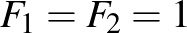 ,
, 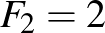 , ... és
, ... és 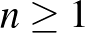 -re
-re 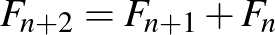 .)
.)
Tegyük fel, hogy 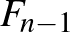 -ig beláttuk az állítást.
-ig beláttuk az állítást.
1. Először tegyük fel, hogy a kavicsok száma 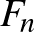 .
.
a) Ha 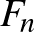 kavics van és Első legalább
kavics van és Első legalább 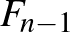 kavicsot vesz el, akkor
kavicsot vesz el, akkor 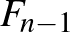 -nél kevesebb kavics marad (
-nél kevesebb kavics marad (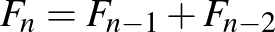 és
és 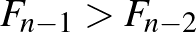 ), így Második az összes megmaradt kavicsot el tudja venni, és nyer.
), így Második az összes megmaradt kavicsot el tudja venni, és nyer.
b) Ha Első kevesebbet vesz el, mint 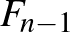 , akkor
, akkor 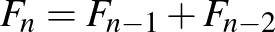 miatt legfeljebb
miatt legfeljebb 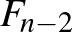 -t vett el. Második gondolatban kétfelé osztja a kavicskupacot, egy
-t vett el. Második gondolatban kétfelé osztja a kavicskupacot, egy 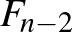 és egy
és egy 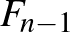 darabszámúra. Mivel az
darabszámúra. Mivel az 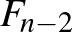 darabszámú kupacos játékban ő második, az indukciós feltevés miatt megnyerheti, és az utoljára elvett kavicsok száma legfeljebb
darabszámú kupacos játékban ő második, az indukciós feltevés miatt megnyerheti, és az utoljára elvett kavicsok száma legfeljebb 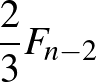 . Ezért az
. Ezért az 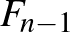 darabszámú kupacból először Első vesz, legfeljebb
darabszámú kupacból először Első vesz, legfeljebb 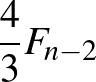 darabot, ami kisebb, mint
darabot, ami kisebb, mint 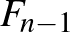 , hiszen
, hiszen 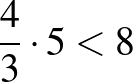 ,
, 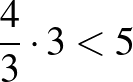 ,
, 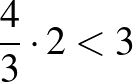 ,
, 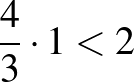 , illetve
, illetve 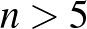 -re:
-re:
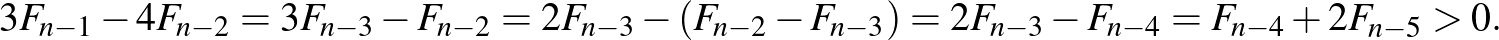
Így az 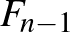 kavicsos kupacban Első nem tud minden kavicsot egyszerre elvenni, ezért (az indukció szerint) abban a játékban is nyerhet Második.
kavicsos kupacban Első nem tud minden kavicsot egyszerre elvenni, ezért (az indukció szerint) abban a játékban is nyerhet Második.
Ebből következik, hogy aki Fibonacci-szám számosságú kavicskupacból elsőként vesz el (akármennyit, de nem az összeset), az veszít.
2. Most tegyük fel, hogy a kavicsok száma nem Fibonacci-szám. A továbbiakhoz több ötletet is felhasználunk.
1. Két szomszédos Fibonacci-szám összege Fibonacci szám.
2. Két másodszomszédos Fibonacci-szám közül a nagyobbik több, mint kétszerese a kisebbiknek: 1 és 2 nem csak másodszomszédos, hanem szomszédos is; míg 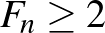 -re
-re 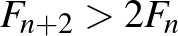 , hiszen
, hiszen 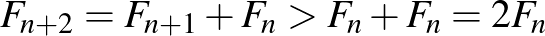 .
.
3. Bármely pozitív egész szám felírható különböző Fibonacci-számok (esetleg egytagú) összegeként. A bizonyítás indukciós gondolata: Az adott számból levonjuk a lehető legnagyobb Fibonacci-számot, és ha van maradék (azaz nem Fibonacci-számból indultunk ki), akkor tovább folytatható az eljárás, mert minden természetes számhoz van nála nem nagyobb Fibonacci-szám. Sőt, ami a levonás után megmarad, az biztosan kisebb, mint az éppen levont számot közvetlenül megelőző Fibonacci-szám, különben két szomszédos Fibonacci-számot vonnánk le, amelyek összege egy nagyobb Fibonacci-szám, így azt előbb megtaláltuk volna. A szám tehát a levont Fibonacci-számok összege, és a felírásban nagyság szerint szomszédosak közül a nagyobbik minden esetben több, mint kétszerese a kisebbiknek.
A stratégia: Tegyük fel, hogy a kavicsok száma 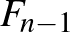 és
és 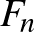 közé esik (de nem egyenlő egyikkel sem). Írjuk fel a kavicsok számát csökkenő Fibonacci-számok összegeként a fenti módon (nyilván
közé esik (de nem egyenlő egyikkel sem). Írjuk fel a kavicsok számát csökkenő Fibonacci-számok összegeként a fenti módon (nyilván 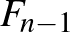 a legnagyobb), és bontsuk szét gondolatban a kavicskupacot ilyen számosságú részekre. Első vegye el a legkisebb tagnak megfelelő darabszámú kavicsot. Mivel Második nem tudja a felírásban következő tagnak megfelelő számú kavicsot elvenni (mert az az elvett kavicsok számának több mint kétszerese), Első úgy tekinti, mintha Második a soron következő Fibonacci-szám számosságú kavicskupacot bontaná meg, és az ehhez a Fibonacci-számhoz tartozó indukciós stratégiát követi: ebben a kupacban ő veszi el az utolsó darabot, és az utoljára elvett kavicsok számának kétszerese kisebb, mint a következő kupacban lévő kavicsok száma. Második a soron következő lépésével új (Fibonacci-szám darabszámú kavicsból álló) kupacot bont, de nem veheti el az összes kavicsot benne.
a legnagyobb), és bontsuk szét gondolatban a kavicskupacot ilyen számosságú részekre. Első vegye el a legkisebb tagnak megfelelő darabszámú kavicsot. Mivel Második nem tudja a felírásban következő tagnak megfelelő számú kavicsot elvenni (mert az az elvett kavicsok számának több mint kétszerese), Első úgy tekinti, mintha Második a soron következő Fibonacci-szám számosságú kavicskupacot bontaná meg, és az ehhez a Fibonacci-számhoz tartozó indukciós stratégiát követi: ebben a kupacban ő veszi el az utolsó darabot, és az utoljára elvett kavicsok számának kétszerese kisebb, mint a következő kupacban lévő kavicsok száma. Második a soron következő lépésével új (Fibonacci-szám darabszámú kavicsból álló) kupacot bont, de nem veheti el az összes kavicsot benne.
Mivel Elsőnek az indukciós feltevés szerint 1-től 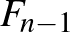 -ig minden Fibonacci-számra van nyerő stratégiája Második ellenében, Első nyer.
-ig minden Fibonacci-számra van nyerő stratégiája Második ellenében, Első nyer.
Az állítást igazoltuk minden számra 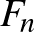 -ig, ezért az indukció elve alapján minden természetes számra igaz az állítás.
-ig, ezért az indukció elve alapján minden természetes számra igaz az állítás.
2.3. Két kupac kavics (kétkupacos NIM játék)
A kavicsok két kupacban vannak. Két játékos felváltva vehet el tetszőleges darabszámú kavicsot abból a kupacból, amelyikből akar. Az nyer, aki az utolsó kavicsot elveszi.
Stratégia: Ha egyforma darabszámú kavics van a két kupacban, akkor Második nyerhet, ha mindig úgy lép, hogy kiegyenlítse a két kupac darabszámát. Ha a kavicsok darabszáma a két kupacban különböző, akkor a kezdő minden lépésével ki tudja egyenlíteni a két kupac darabszámát.
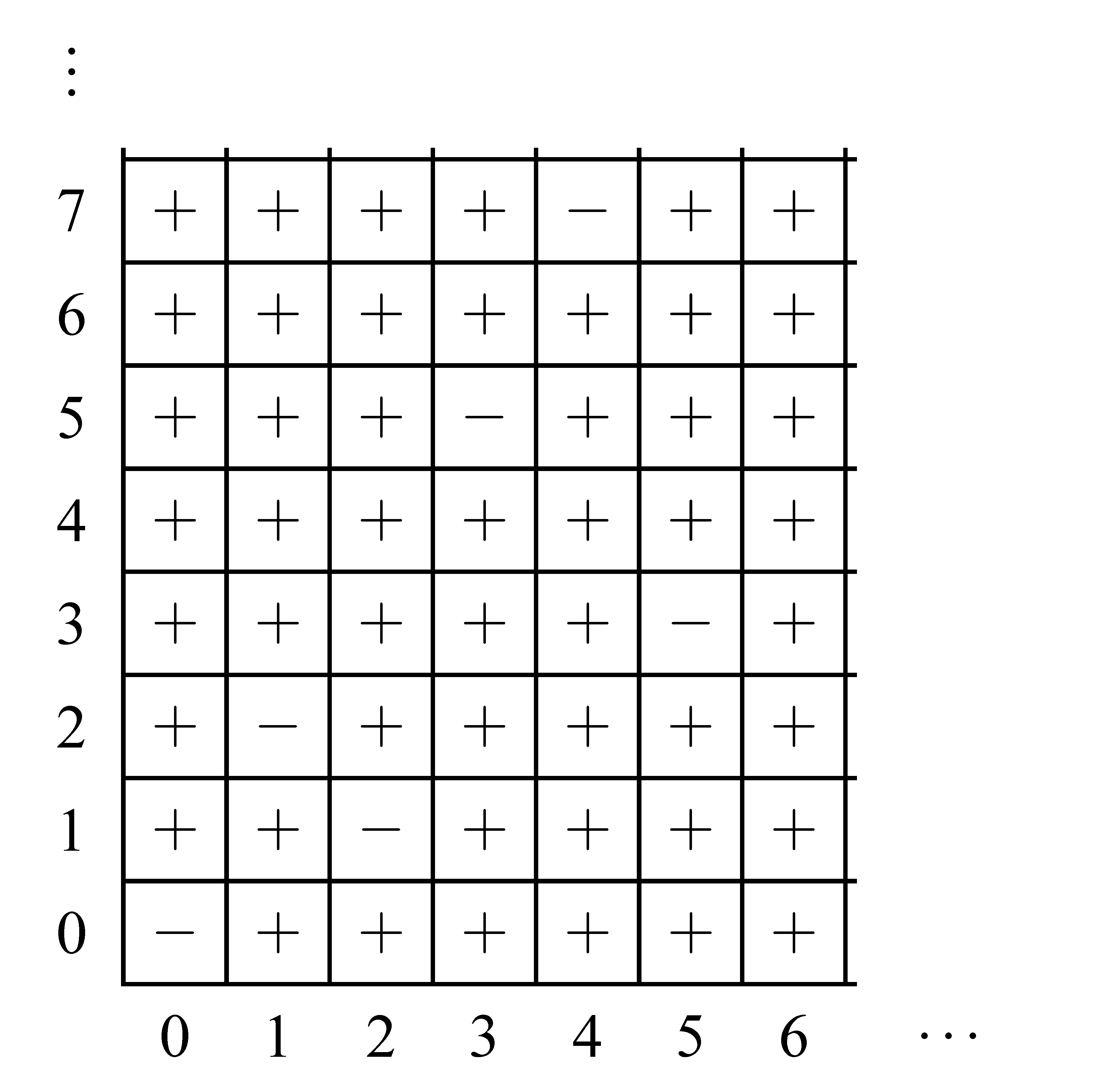
Megjegyzés: A játék úgy is játszható, hogy kavicsok helyett egy rácstéglalapot veszünk. Ennek jobb felső mezőjén áll egy bábu. Ezzel a bábuval lehet balra és lefelé lépni. Az nyer, aki a bal alsó sarokban lévő mezőre lép. (A két játékot összevetve: annyit lép egy játékos a rácstéglalapon, ahány kavicsot elvett volna egy kupacból, mégpedig az egyik kupac esetén lefelé, a másiknál balra.)
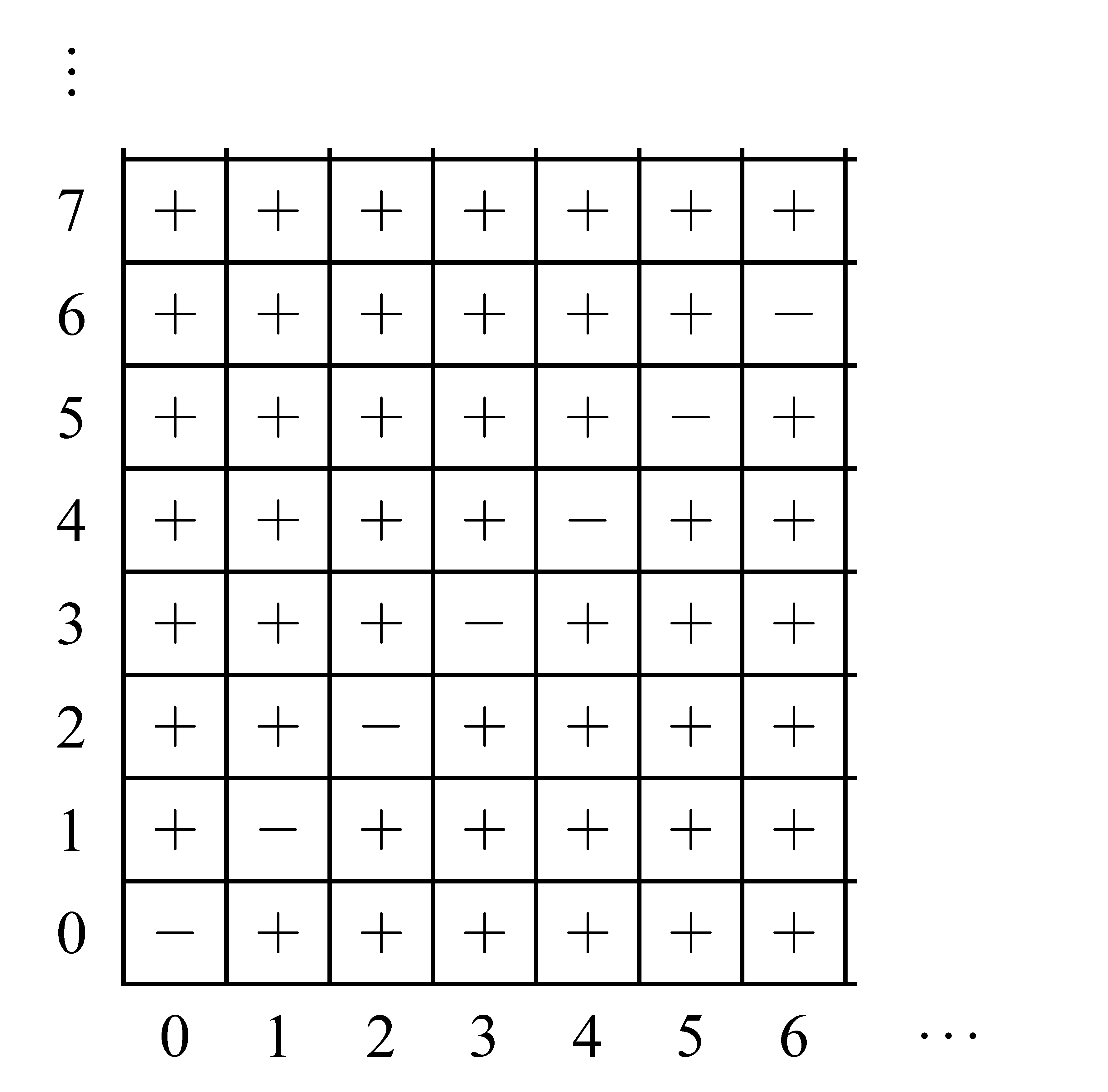
 ) és a vesztő (–) pozíciók jelölését az éppen lépésre következő játékos szempontjából.
) és a vesztő (–) pozíciók jelölését az éppen lépésre következő játékos szempontjából. mező), akkor a másik nyert (–). Minden olyan mező, ahonnan a
mező), akkor a másik nyert (–). Minden olyan mező, ahonnan a 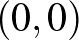 -ra lehet lépni, nyerő (
-ra lehet lépni, nyerő (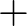 ). A továbbiakban ahonnan csak
). A továbbiakban ahonnan csak 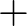 jelű mezőre lehet lépni, az – jelet kap. Ahonnan pedig lehet –ra lépni, az nyerő,
jelű mezőre lehet lépni, az – jelet kap. Ahonnan pedig lehet –ra lépni, az nyerő, 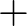 jelet kap stb.
jelet kap stb.Látható, hogy egyenlő számú kavics esetén, vagyis ha a tábla négyzetes, a kezdő veszít (ellenfele jó játéka esetén).
Ezt a játékot is játszhatjuk úgy, hogy az veszít, aki az utolsó kavicsot veszi el. A nyerő stratégiát a táblás módszerrel egyszerű megtalálni.
A kavicskupacos játékot három vagy több kupaccal is játszhatjuk. A három kupacos játék NIM néven is ismert, amelynek kiterjedt irodalma van. A játék részletes elemzése olvasható például Lánczi Ivánné munkájában (Szórakozás számrendszerekkel, Matematikai érdekességek, szerkesztő Hódi Endre, 91–109. oldal, Gondolat kiadó, 1969).
2.4. Két kupac kavics van, amelyekből a következő szabály szerint vehet el felváltva a két játékos: bármelyik kupacból lehet elvenni akármennyit, vagy szabad elvenni mindkét kupacból ugyanannyit.
Stratégia: Ennek a játéknak a stratégiáját a táblás analógia nélkül nehezebb megtalálni. A táblán, rajzban, egyszerűen megjelölhető a nyerő pozíciók helye.
ELTE TTK Matematikai Intézet, Matematikatanítási és Módszertani Központ









