1. Bevezető
A 2019/20-as tanév második féléve és a 2020. májusi érettségi időszak hosszú ideig emlékezetes lesz minden diák, tanár és szülő számára. A COVID-19 vírus[1] terjedése miatt elrendelt iskolaépület-bezárások, a tanítás napok alatt történő átállítása digitális távoktatásra, majd az írásbeli érettségi vizsgák lebonyolítása mindenkitől extra erőfeszítést, nagyfokú rugalmasságot és magas fokú alkalmazkodóképességet igényelt. Utólag visszatekintve összefoglalva azt mondhatjuk, hogy mindenki igyekezett a lehető legjobban teljesíteni ebben a helyzetben, a tanévet le lehetett zárni, az érettségi vizsgák rendben lezajlottak. Ugyanakkor pár dolgot nyilvánvalóvá tett ez a két-három hónap: ezek közül talán a legfontosabb, hogy iskolára (mint fizikai térre) és pedagógusra szükség van a 21. században is.
Az alábbi cikkben a 2020. évi matematika érettségi vizsga rövid elemzését végezzük el. Tesszük ezt azért (is), mert az idei Rátz László Vándorgyűlés elmaradása miatt a megszokott elemzésünket nem tárhattuk szóban az érdeklődők elé. Szeretnénk a legfontosabb eredményességi statisztikákat és néhány érdekesebbnek bizonyuló feladatot részletesebben is bemutatni, mindezt külön közép- és emelt szinten, a magyar nyelvű feladatsorokat tekintve.
Mielőtt a részletesebb elemzésnek nekifogunk, fontosnak tartunk eloszlatni egy „városi legendát”: az idei írásbeli feladatsorok összeállítását semmilyen módon nem befolyásolta a vírushelyzet. A feladatsorok még március előtt elkészültek, a minden évben megszokott tartalommal és szerkezetben. A tételek összeállítását végző bizottság azt sem tudta figyelembe venni, hogy az emelt szintű vizsgázók idén szóbeli vizsga nélkül tehetik le a vizsgát, hiszen erről csak pár héttel a vizsga előtt született döntés. (Egyébként sem világos, hogy – ha lett volna erre mód – ezt hogyan lehetett/kellett volna figyelembe venni a feladatsorok elkészítésénél.) Ezen túl is megalapozatlan minden olyan, időnként szárnyra kapó feltételezés, mely szerint az aktuális feladatsor „biztosan szándékosan ilyen vagy olyan” (pl. a szokásosnál könnyebb vagy nehezebb) volt, hiszen a vizsgázók elé kerülő feladatsort nem sokkal a vizsga előtt sorsolják ki általában három feladatsor közül.
2. Megoldottsági adatok, érdekesebb eredmények
Az alábbi elemzésben szereplő adatok jelentős részben az iskolák által évek óta végzett önkéntes adatszolgáltatásból származnak, amit ezúton is köszönünk! Ilyen módon idén a középszintű vizsgák 36,1, az emelt szintű vizsgák 26,4%-áról van részletesebb információnk. Az elmúlt évek hasonló mérései alapján elmondható, hogy a teljes vizsgázói populáció eredményei általában 3-4 százalékponttal elmaradnak az önkéntes adatszolgáltatásból származó eredményektől.
2.1. Középszint[2]
A középszintű matematika érettségi vizsgát érintette talán a legkevésbé az idei járványügyi helyzet, hiszen a „nagy” tárgyak közül ez az egyetlen, amiből normál körülmények között sincs szóbeli vizsga. (Ez alól természetesen kivételt képeznek azok a diákok, akik az írásbeli vizsgán 12 és 25% közötti eredményt értek el, nekik idén is volt lehetőségük szóbeli vizsgát tenni.)
Idén végül 64 239-en kísérelték meg a vizsgát középszinten, közülük magyar nyelven 62 356-an vizsgáztak. Ez a szám több okból is alacsonyabb a korábbi években mért adatnál. Egyfelől közismert, hogy ezúttal hátrányos következmények nélkül vissza lehetett lépni az érvényes vizsgajelentkezéstől. Másfelől a korábbinál többen tettek idén emelt szintű vizsgát matematikából. (Egy harmadik ok a végzős diákok számának folyamatos, demográfiai hátterű csökkenése.)
A 2020. évi magyar nyelvű feladatsor megoldottsága – az önkéntes visszajelzés alapján – 53,4% volt. Ez az adatgyűjtés 2012-es kezdete óta mért legmagasabb érték: a megelőző 8 évben az eredményesség mindig 44,6 és 53% közé esett. Mint említettük, ezek az értékek néhány százalékponttal mindig meghaladják a teljes populációra vonatkozó adatokat: idén az összes magyar nyelven vizsgázó írásbeli eredményének átlaga 50,2% volt, ami a 2017-es 50,4% után a második legmagasabb érték.
Eredményesség vizsgarészenként, feladatonként, alfeladatonként
Középszint, I. rész
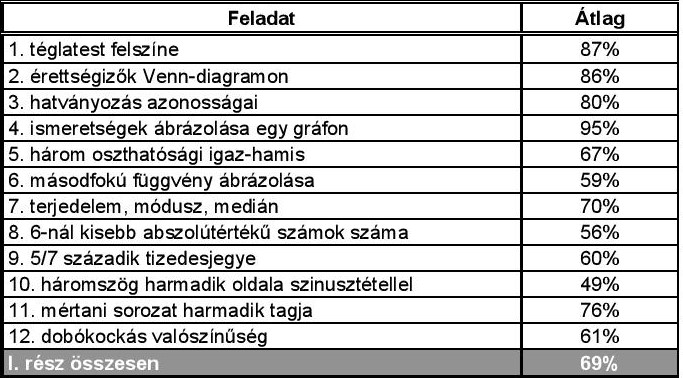
– A középszintű feladatsor I. részéről összességében az mondható el, hogy az átlagosnál jobban sikerült (2012 óta ennek a vizsgarésznek az átlaga 63% volt), sőt, az egyik legjobb eredményt hozta az elmúlt 10 évben (csak 2014-ben és 2018-ban volt ennél magasabb e vizsgarész megoldottsága).
– Az első négy feladat jó indítás volt: ezek a feladatok megnyugtathatták a diákokat, hiszen 80% feletti megoldottságot eredményeztek. Ezen belül is kiemelkedő a 4. feladat, amely minden idők második legjobb eredményét hozta (az első helyen a 2019. évi feladatsor 8. feladata áll, 97%-os megoldottsággal).
– Érdemes még kiemelni a 7. feladat megoldottságát. Egy nem szokványos, sem korábbi érettségi feladatsorokban, sem tankönyvekben nem szereplő feladatot kellett megoldani: egy kördiagram alapján egy adatsokaság különböző statisztikai jellemzőit leolvasni.
– A kevésbé jó megoldottságot mutató 8-as feladat egy korábbi hasonló példa (2017-ben 40%-os megoldottsága lett annak a feladatnak, amelyben a 3-nál kisebb abszolútértékű számokat kellett ábrázolni egy számegyenesen) alapján nem jelentett meglepetést, mint ahogy a 10. feladat alacsony eredményessége sem váratlan.
Középszint, II. A rész

– A feladatsor II. részének három feladatáról (és benne a kilenc alfeladatról) elmondható, hogy általában közepes nehézségűnek bizonyultak; felfelé lógott ki – nem meglepő módon – a 14. feladat a) része, lefelé – mértékét tekintve talán meglepő módon – a 15/c alfeladat.
– Talán meglepőnek mondható a 15. feladat c) részének alacsony megoldottsága. Ez alapján úgy tűnik, hogy egy egyszerű modellezési helyzet is komoly nehézséget jelent a diákok nagy része számára. Biztosak lehetünk benne, hogy nem a felírt egyenlet megoldása okozza a problémát, hiszen a 13/a alfeladatban ennél nehezebb egyenletet oldanak meg jóval eredményesebben a diákok.
– Végül megemlítjük, hogy a (valós eredményekre épülő) 14-es feladat nagy sikert aratott a közösségi médiában, a benne szereplő Márton Anita büszkén írta, hogy érettségi tananyag lett[3]. Ha nem maradt volna el idén az olimpia, talán még érdekesebb lett volna a feladat a nagyközönség számára.
Középszint, II.B rész
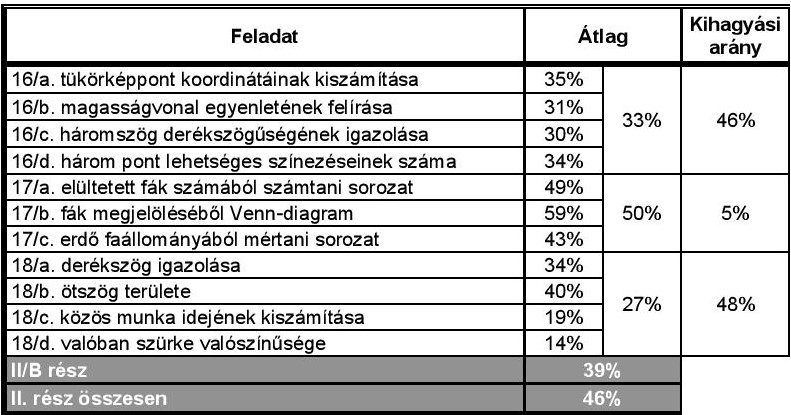
– A feladatsor II.B részének érdekessége abból a jelenségből fakad, hogy a 17. feladatot a vizsgázók 95%-a választotta. Ez 2012 óta a második legmagasabb arány (2012-ben a 16-os feladatot 97% választotta). Lehet azon vitatkozni, hogy mennyire helyénvaló egy olyan „választható” feladat, ami tulajdonképpen nem az, hiszen majdnem mindenki tetszését elnyeri. Azonban az a jelenség, amikor egy feladatot sokan választanak, de a másik két feladat között nagyjából egyenlő arányban oszlanak meg a vizsgázók, mindenképpen örömtelibb, mint amikor a feladatsorban egy nagyon elutasított feladat szerepel, és így valójában nagyon leszűkül a választás lehetősége a diákok számára (2012-ben ez volt a helyzet a 18. feladattal, melyet a vizsgázók 76%-a kihagyott).
– A 17. feladat népszerűsége mögött a benne szereplő témakörök (sorozatok, logikai szita formula) kedveltsége és az ilyen típusú feladatok viszonylag gyakori megjelenése állhat.
– Meglepően alacsonynak mondható a 16/a alfeladat megoldottsága, ehhez ugyanis nagyon minimális matematikai ismeret szükséges. A 18/c alfeladat esetében is talán jobb eredményt vártunk: annak ellenére, hogy a feladat nem csak egyenlettel, hanem következtetéssel is megoldható, kevés jó megoldás született.
– Nem nevezhető meglepően alacsonynak a 18/d alfeladat eredményessége, a binomiális eloszlás alkalmazása továbbra sem megy a diákoknak, pedig az utóbbi időben minden évben volt ilyen feladat a középszintű feladatsorban. Igaz, rendre a mostanihoz hasonló megoldottsággal (pl. 2018. május 18/c feladat: 10%).
2.2. Emelt szint[4]
A megelőző évekhez képest 2020-ban két olyan meghatározó új momentum volt az emelt szintű matematika vizsgán, amely befolyásolta a vizsga átlageredményét.
A felsőoktatási felvételihez előírt legalább egy kötelező emelt szintű vizsga számottevően megnövelte az emelt szinten jelentkezők számát: 2020-ban (a jelentkezésüket a járvány miatt visszavonók nélkül) összesen 4801-en jelentkeztek emelt szintű vizsgára, ami 36%-kal több az elmúlt öt év átlagánál, és a kétszintű vizsgarendszer bevezetése óta messze a legmagasabb érték. Jogos a feltételezés, hogy a pluszban megjelent jelentkezők jelentős része olyan vizsgázó, akiket csak a kényszer terelt ebbe az irányba, és így az emelt szinten vizsgázók „átlagos felkészültsége” valamivel csökkent az előző évekhez képest. (Ők ugyanekkor eltűntek a középszinten vizsgázók közül, de a középszinten vizsgázók jóval nagyobb száma miatt az eltűnésük hatása nem vagy csak alig érzékelhető.)
A másik tényező a szóbeli vizsga elmaradása. Bizonyára sokan nem bánták, hogy elhagyhatták az ehhez szükséges hosszadalmas, alapos elméleti felkészülést. Másrészt viszont a szóbeli nélküli érettséginek az volt az ára, hogy a vizsgaeredmények átlaga bizonyosan alacsonyabb lett, mint szóbeli vizsgával együtt lett volna.
A szóbeli vizsgák átlageredménye igen erős stabilitást mutat: az elmúlt 10 évben 75,2 és 77,6% között ingadozott. Ugyanebben a periódusban a legjobban sikerült írásbeli átlag 69,4% volt, a 10 év írásbeli átlaga pedig 65,7%. Az elmúlt évtizedben a matematika szóbeli vizsgák átlaga kb. 10 százalékponttal haladta meg az írásbeli vizsgákét. A szóbeli vizsga kisebb súlya miatt ez annyit jelent, hogy a vizsgák átlageredménye kb. 2,5 százalékponttal jobb, mint az írásbeli átlageredmény. Ez a hatás tehát idén a vírus miatt elmaradt.
A szóbeli elmaradásának még egy érdekes hatása lett. Elég közismertek a középszintű tárgyak pontszámeloszlásának „tüskés” diagramjai, ahol az egyes osztályzatok alsó határán kiemelkedően sok, az alatt 1-2 ponttal pedig nagyon kevés dolgozat található. Ez talán nem meglepő azoknál a tárgyaknál, ahol van szóbeli vizsga, hiszen minden vizsgáztató tudja feleltetéskor, hogy n pont kell a négyeshez, és ilyenkor csak nagyon kevesen adnak n – 1 vagy n – 2 pontot, annál többen n-et vagy n + 1-et. (Igaz ez annak ellenére, hogy az érettségin az osztályzatnak csak szimbolikus jelentősége van.) Kicsit már meglepőbb, hogy ugyanezt a képet látjuk évről évre a matematika középszintű vizsga pontszámeloszlásánál is, pedig ez (a viszonylag kevés szóbeliző kivételével) egy (objektívebbnek tartott) írásbeli vizsgából származik. De őszintén: tegye fel a kezét közülünk az, aki nem talál bármelyik dolgozatban még 1-2 pontot, ha nagyon kell… Idén az egyes osztályzatok (illetve a szóbelihez szükséges érték) alsó határán 5613, 1 ponttal alatta 728 dolgozat volt.
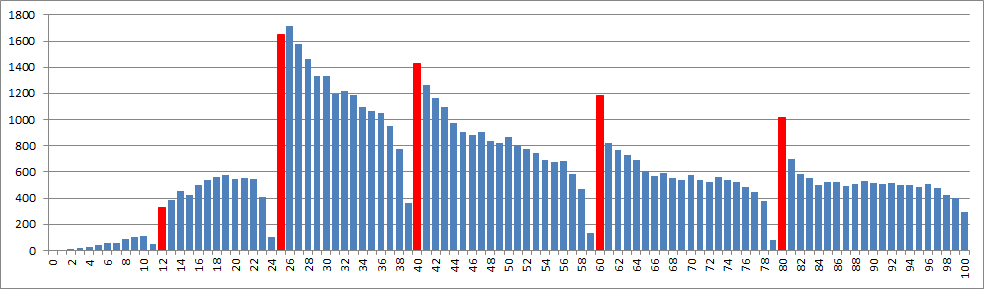
1. ábra. A 2020. évi magyar nyelvű középszintű matematika érettségi vizsga írásbeli részén elért pontszámok eloszlása a vizsgázók körében
A szóbeli elmaradása miatt felmerülhetett, hogy ez a jelenség idén emelt szinten is láthatóvá válik. De az emelt szintű dolgozatok javítása intézménytől függetlenül történik: mondjuk Kovács Piroskának (saját tanítványunknak) nyilván motiváltabban keresünk még egy pontot (ha ennyi hiányzik az ötöshöz), mint a 01/K04M//6918/15 jelű vizsgázónak, másrészt a 115 pontos maximum, és 33, illetve 47%-os határok miatt a ponthatárok sem magától értetődőek. Kiderült azonban, hogy a javítók még így is odafigyeltek az osztályzatok ponthatáraira: az egyes osztályzatok alsó határán 289, egy ponttal alatta 114 dolgozat volt. Nem meglepő, hogy leginkább a jeles és az elégséges határán figyelhető meg a jelenség: 69 pontos dolgozat 106, 68 pontos 36; 29 pontos dolgozat 49, 28 pontos pedig 4 darab volt.
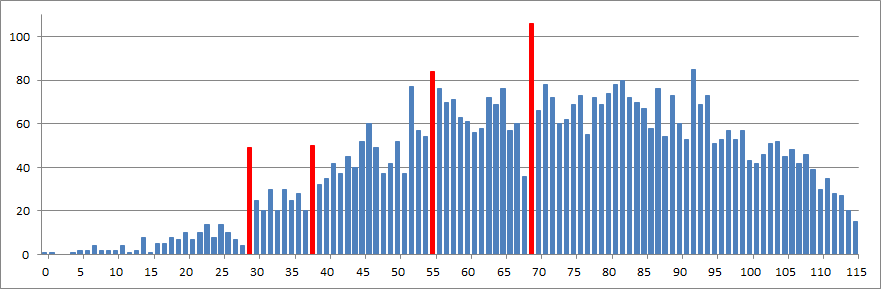
2. ábra: A 2020. évi magyar nyelvű emelt szintű matematika érettségi vizsga írásbeli részén elért pontszámok eloszlása a vizsgázók körében
Idén magyar nyelven 4722-en vizsgáztak. A 2020. évi magyar nyelvű feladatsor megoldottsága – az önkéntes visszajelzés alapján – 66,8% volt. Ez az adatgyűjtés 2012-es kezdete óta (a 2013-as 61,9% után) a második legalacsonyabb érték, és kb. 3-4 százalékponttal marad el a 8 év átlagától. Ezt a különbséget talán éppen betudhatjuk az idén megjelent 36%-nyi plusz vizsgázónak[5]. Adataink emelt szinten is néhány százalékponttal meghaladják a teljes populációra vonatkozó adatokat: idén az összes magyar nyelven vizsgázó írásbeli eredményének átlaga 62,1% volt.
Vizsgarészenként, feladatonként, itemenként
Emelt szint, I. rész

Az I. rész átlagos megoldottsága 71% lett, ami csak kevéssel marad el a 2012 óta mért 75%-os átlagtól. Az első négy feladat a számok alapján egyenletesen nehezedett. Az 1. feladat jó „bemelegítő” volt, 86%-os megoldottságánál csak két jobbat mértünk az elmúlt 8 évben (2012/1. 92%, 2014/1. 88%). Még ezen belül is kiemelkedik az a) feladat 97%-os eredményessége: erre a vizsgázók 92%-a megkapta a maximális 5 pontot.
Ennek ellenpontja a 4. feladat: a másodfokú témakörből feltett viszonylag száraz, elméleti kérdések az elmúlt években némileg visszaszorultak a tanítási gyakorlatban, és talán ez tükröződik a feladat relatíve alacsony megoldottságában (csak a 7. feladat sikerült ennél rosszabbul). A 4/c feladat az egész feladatsornak (a 7/c után) a második leggyengébben sikerült iteme lett, pedig nemcsak „ötletesen”, de „mechanikusan” is meg lehetett (volna) oldani. Ennek ellenére a vizsgázók 45%-a 0 pontot kapott rá.
Emelt szint II. rész
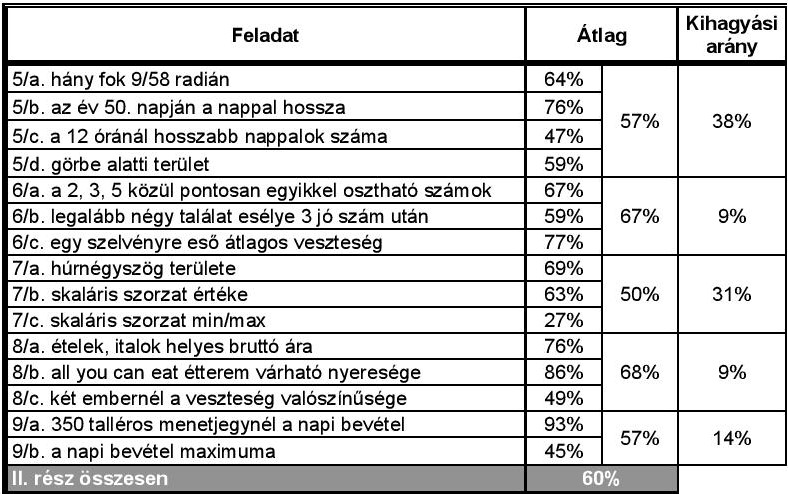
Nem volt könnyű a II. rész nyitánya, és megszokott sem volt, bár ez a két jellemző valószínűleg összefügg: a nehézség jelentős részben éppen a szokatlanságból következik. Noha az a) és a b) kérdés próbálta felvezetni a c)-t, már a felvezetőnek szánt 5/a feladat megoldottsága is csak 64%-os lett. Radiánban ilyen módon érettségin, de még tanórán is csak ritkán kell számolni – viszont itt derül ki igazán, hogy ki az, aki valóban érti is az ívmértéket. A vizsgázók 38%-ának az volt erre a helyzetre a válasza, hogy ezt a feladatot hagyta ki. Talán jobb helyen lett volna ez a feladat kicsit hátrébb a feladatsorban.
A másik népszerűtlen feladat a 7. volt (31%-os kihagyási arány), ennek is a c) részével gyűlt meg a baja a legtöbb vizsgázónak. Ha nem csak kiszámítani kell, akkor a skaláris szorzattal sem könnyű dolgozni, pláne ha a szélsőértékét kell meghatározni. Az item megoldottsága 27%-os lett, a vizsgázók 13%-a kapott maximális (7), 54%-a 0 pontot a feladatra.
A 6. és a 8. feladat ehhez képest nem okozott problémát, és utolsó feladatként a 9.-ben elért 60% is elfogadhatónak számít, bár itt elég markáns különbség volt a két alfeladat megoldottsága között (93, illetve 45%).
Mi várható ősszel?
Ahogy említettük, a járvány miatt idén hátrányos következmények nélkül vissza lehetett vonni az érvényes vizsgajelentkezéseket. Ezzel a lehetőséggel matematikából középszinten 2676-an (az összes jelentkező 4%-a), emelt szinten 281-en (az összes jelentkező 5,5%-a) éltek. Feltételezhető, hogy közülük sokan úgy tervezték, hogy a soron következő őszi vizsgaidőszakban teszik le az elmaradt vizsgát. Amióta ősszel nem lehet matematikából előrehozott vizsgát tenni (tehát 2014 óta), az őszi vizsgák jelentős részét (80%-át) a tavasszal valamilyen tárgyból év végén vagy az érettségin megbukók vizsgái teszik ki. Amennyiben a jelentkezéstől most visszalépők valóban nagy számban jelentkeznek ősszel, akkor egyrészt a vizsgázók száma a megszokott létszám 2-3-szorosára emelkedhet, másrészt a vizsgázók képességeloszlása is a szokásostól jelentősen eltérő képet fog mutatni: az előző évekhez képest magasabb átlageredményekre számíthatunk – feltéve természetesen, hogy a járványhelyzet az őszi vizsgaidőszak rendes megtartását nem befolyásolja.
3. Összefoglalás
Összefoglalásképpen elmondhatjuk, hogy a 2020. évi matematika érettségi vizsga a nehezített és különleges körülmények ellenére nem mutatott jelentősen eltérő képet, mint az előző években. Emelt szinten az írásbeli kicsit alacsonyabb eredménye valószínűleg a vizsgázók számának bővülése miatt következett be, ezt a hipotézist az elkövetkező – remélhetőleg vírus- és karanténmentes – évek eredményei támaszthatják alá. Abban is bízunk, hogy 2021-ben újra élőszóban tarthatjuk meg az Érettségiről érdekesen előadásunkat a matematikatanárok országos Rátz László Vándorgyűlésén.
4. További irodalom
A 2012. május-júniusi érettségi feladatsor és az egyes feladatok mérésmetodikai vizsgálata
http://www.oktatas.hu/pub_bin/dload/unios_projektek/tamop318/meresmetodika/Matematika.pdf
Érettségi vizsgatárgyak elemzése 2009-2012. tavaszi vizsgaidőszakok
A kétszintű érettségi rendszerrel kapcsolatos változtatási igények felmérése a gyakorlati tapasztalatok alapján
A közép- és emelt szintű értékelési skálák összehasonlítása
Az ellenőrzés problémaköre az érettségin http://matek.fazekas.hu/index.php?option=com_content&view=article&id=296:ellenorzes-es-valasz&catid=34&Itemid=223 (rövid kivonat:) KöMaL, 2015. október
A matematika érettségi vizsga 2017-től (RLV 2015) http://rlv.berzsenyi.hu/2015/Koncz_Csapodi.ppsx?attredirects=0&d=1
Eredményesség és számológép-használat az érettségi vizsgán (RLV 2016)
Amit tudtunk, amit sejtettünk, és amit nem gondoltunk volna a matematikaérettségiről (RLV 2017) http://rlv.berzsenyi.hu/2017/Csapodi-Koncz_Matematikaerettsegi_RLV17_KL.ppsx
Az érettségiről érdekesen (RLV 2018) http://www.bolyai.hu/RLV2018/Csapodi_Koncz.ppsx
Csaba Csapodi and Levente Koncz: The efficiency of written final exam questions in mathematics based on voluntary data reports, 2012–2015. Teaching Mathematics and Computer Science, 2016/14 p63-81) http://tmcs.math.unideb.hu/load_doc.php?p=306&t=abs
A matematika érettségi vizsga elemzése 2005-2015 (Csapodi Csaba doktori értekezése) https://dea.lib.unideb.hu/dea/handle/2437/236563
Hivatkozások
[1] Egy olyan cikkünkre hívjuk fel az olvasók figyelmét, amely egy pár évvel ezelőtti emelt szintű érettségi feladatsorban szereplő feladatról, és azon belül a pandémia során a gyakorlatban is felmerülő problémákról szól: https://index.hu/techtud/2020/05/08/a_2017-es_matekerettsegi_megjosolta_a_jarvanyt/
[2] A 2020. májusi magyar nyelvű középszintű feladatsor: http://dload.oktatas.educatio.hu/erettsegi/feladatok_2020tavasz_kozep/k_mat_20maj_fl.pdf
A javítási-értékelési útmutató: http://dload.oktatas.educatio.hu/erettsegi/feladatok_2020tavasz_kozep/k_mat_20maj_ut.pdf
[3] http://www.nemzetisport.hu/atletika/erettsegi-megoldottuk-marton-anitat-rioi-dontoje-szerepelt-a-tetelsorban-2760979
[4] A 2020. májusi magyar nyelvű emelt szintű feladatsor: https://www.oktatas.hu/bin/content/dload/erettsegi/feladatok_2020tavasz_emelt/e_mat_20maj_fl.pdf
A javítási-értékelési útmutató: https://www.oktatas.hu/bin/content/dload/erettsegi/feladatok_2020tavasz_emelt/e_mat_20maj_ut.pdf
[5] Megerősíti ezt a feltételezést, hogy ugyanez volt a helyzet valamennyi „nagy” vizsgatárgynál: az idei eredmények 2-13%-kal elmaradnak a megelőző évek átlagától.
Csapodi Csaba, ELTE TTK, Matematikai Intézet
Koncz Levente, Óbudai Árpád Gimnázium









