Információk

 Aktuális szám: 6. szám 2017. december 

Miért éppen LaTeX?

Miért éppen LaTeX?

Az elmúlt években, évtizedben rendszeresen fordultak hozzám ismerőseim LaTeX-et (ejtsd: léteh vagy magyarosan lateh) illető kérdésekkel. Szerettem volna segíteni nekik, és — bár bevallom, sokszor nem is tudtam a válaszokat — minden kérdésnek igyekeztem a végére járni. Közben sokat tanultam magam is, és az, hogy továbbra is szeretnék segíteni mindazoknak, akik kíváncsiak a LaTeX-re, nem változott.

Na, igen, persze ha az elején akarom kezdeni, akkor először idéznem kell a leggyakrabban hallott kérdéseket (amelyekre később igyekszem is válaszolni):

Mi az a LaTeX?
Mire jó a LaTeX?
Jó a LaTeX?
Érdemes-e LaTeX-et tanulni?
Kinek érdemes LaTeX-et tanulni?
Miért érdemes LaTeX-et tanulni?
Meg lehet-e tanulni a LaTeX-et?
Érdemes-e megtanulni a LaTeX-et?
Nehéz megtanulni a LaTeX-et?
Miért nehéz megtanulni a LaTeX-et?

Magamtól senkinek sem mondanám, hogy tanulja meg a LaTeX-et, legfeljebb tanácsolnám, ha például megkérdezné hogy „Matematikai szöveghez milyen tördelő programot érdemes használni?”. De ismerjük el, nagyon csekély az esélye annak, hogy valaki éppen ezzel a kérdéssel álljon elő.

Tény azonban, hogy egy matematikatanárnak nagy segítségére lehet. És mivel sajnos a LaTeX-et is lehet rosszul használni, szeretnék segíteni, hogy ez ne így legyen.

Én egy nap alatt tanultam meg az alapokat, és azóta is folyamatosan tanulok. Minden nap örömömet lelem abban, hogy szép dokumentumok kerülnek ki a kezem alól. Ennek az örömnek szeretném a kedves olvasókat is részesévé tenni.

Nyomdászat

Réges-régen, úgy 60-80 évvel ezelőtt a legtöbb nyomdai termék még kézzel készült. A szöveg nyomdai előállítása azt jelentette, hogy az ólombetűket sorba szedte a szedő, a sorokat egymás alá illesztette egy nagy keretbe, majd a keretből összeállt oldalról lenyomat készült. (Persze visszafelé, tükörírással kellett szedni, hogy a lenyomat megfelelően álljon.) Ez igen fárasztó és nagyon sok hibalehetőséget magában rejtő folyamat volt.

Nem csoda, hogy a nyomdákban már a számítógépek elterjedése előtt megjelentek a szedést könnyítő gépek. A fényszedőgépet két magyar mérnök, Szemző János és Uher Ödön találta fel 1928-ban.

A folyószöveg szedése ezzel jelentősen könnyebbé és gyorsabbá vált, valamint a hibalehetőség is jelentősen csökkent. Ám a képek beillesztése vagy a képletek tördelése továbbra is kézzel történt.

A számítógépek elterjedésével sokan felismerték, hogy a gép képes lehet helyettesíteni a nyomdai munkálatok egy részét. (Bár a sokszorosítást vagy a grafikát nem.) Donald E. Knuth 1962-ben kezdte írni a Számítógép programozás művészete című, többkötetes művét. 1976-ban nekilátott, hogy az addigra elkészült kötetek közül a másodikat újra nyomda alá rendezze, de technikai akadályokba ütközött. Ezek elhárítására — mintegy kilenc év alatt — megalkotta a TeX (ejtsd tech vagy teh) technikai (műszaki) szövegszedő programot. Nem ez volt az első kísérlet, hogy matematikai szövegszedő programot készítsenek, ám ez bizonyult a feladatra legalkalmasabbnak, ugyanis az Amerikai Matematikai Társulat (AMS) is elfogadta, és a továbbiakban ajánlotta is a használatát a matematikai kiadványok előállításához. Ezt elősegítendő egységes formátumokat, stílusokat, betűkészleteket adtak közre (AmS-TeX csomagok).

A professzionális megjelenés mellett hallatlan előnye volt a programnak a szabad fejleszthetőség. Ahogy terjedt a program, egyre többen és egyre jobb kiegészítőket írtak hozzá.

A legnagyobbat talán Leslie Lamport adta hozzá, aki LaTeX néven publikált programjában megvalósította azt a sokak által hiányolt készséget, hogy az automatikusan kezelje a matematikában oly gyakran előforduló számozott egyenletek, tételek, ábrák, táblázatok, hivatkozások stb. számát. Ez azt jelentette, hogy nemcsak hogy automatikusan kitette a számot, hanem azt is, hogy ezekre automatikusan (a számuk ismerete nélkül is) lehetett hivatkozni.

Utóbb az AmS csomagokat is integrálták a LaTeX-be, és mivel a TeX képezi az alapját, így ez az idők folyamán nagyon hatékony programmá fejlődött.

Bár amikor a LaTeX-hel találkoztam, a TeX-et már vagy 20 éve használtam (professzionális szinten), ezért nehezen szántam rá magamat a váltásra, de meggyőződésem, hogy a LaTeX megkerülhetetlen.

Manapság sokkal egyszerűbb publikálni (bármit is), mint a TeX születésekor, és sokan saját maguk készítenék el legszívesebben a kiadványukat, gondolván, hogy az alkalmas a publikációra. Ezeket rendszerint sem szerkesztő, sem tipográfus, sem nyomdász nem látja, ezért nagyon csúnya szövegeket (is) lehet látni nyomtatásban, de különösen az interneten. Ám akit ez zavar, annak érdemes megtanulnia, hogyan lehet szépen szedni. Ehhez nagy segítséget a nyújt LaTeX, én pedig a LaTeX-hez szeretnék segítséget nyújtani.

Kérdések és válaszok

Mi az a LaTeX? Mire jó a LaTeX?

A LaTeX olyan, bárki által ingyenesen hozzáférhető program, amelynek segítségével nyomdai minőségben lehet műszaki szöveget előállítani. Röviden: műszaki szöveg szedő program. Ma a piacon még csak hasonló más program sincs. Van, amelyik képes nyomdai minőséget előállítani, de nem kezeli jól a képleteket. Van, amelyik képletszerkesztővel készült képleteket képként befogad, de azok beillesztése meglehetősen macerás. Van olyan program, amelyiknek van beépített képletszerkesztője, de nem szövegszedő, csak szövegszerkesztő program. (A szövegszerkesztő nem képes sok, a nyomdai minőséghez elengedhetetlen beállítás automatikus alkalmazására.)

Ráadásul a piacon található szövegszedő programok általában nem tudják automatikusan „befolyatni” a szöveget, míg a TeX néhány vezérlőparancs beírása után szinte tévedhetetlenül és automatikusan állítja elő a nyomdai minőségű szöveget.

Az első élményünk (ha helyesen telepítettük a gépre a szükséges programokat) gyors, látványos és lenyűgöző lesz.

Jó a LaTeX?

A rövid válasz: jó. A hosszú válasz: nagyon jó. Az igazság azonban az, hogy nem mindig tökéletes, de javítható.

Érdemes-e LaTeX-et tanulni? Kinek érdemes LaTeX-et tanulni? Miért érdemes LaTeX-et tanulni?

Mindenképpen érdemes. Elsősorban érdemes azoknak, akik valaha az életben matematikát akarnak írni, illetve azoknak is, akik nyomdai minőségű kiadványt akarnak készíteni. Azért érdemes, mert nagyon sokszínű, és a műszaki tördelésen kívül egyéb kiadványok tördelésére is kiválóan alkalmas. Én magam is nagyon sokféle kiadványhoz használtam már TeX-et: szakácskönyv, szépirodalmi mű, társasjáték tábla, plakát, történelmi szemelvénykönyv, statisztikai kiadvány, matematikai cikkek, dolgozatok és természetesen rengeteg matematikakönyv.

Meg lehet-e tanulni a LaTeX-et? Érdemes-e megtanulni a LaTeX-et?

Tanulni lehet, megtanulni nem. És nem is érdemes. Ahogyan a nyelvet használjuk, de nem ismerjük minden szavát, helyesírási szabályát, úgy a LaTeX is megtanulhatatlan, de ettől még jól használható. Állandó rendelkezésünkre állnak az online „szótárak”, a „szabályok” leírása. Ráadásul állandóan fejlődik, mert a LaTeX közösségi fejlesztése nem áll le egy percre sem.

Nehéz „megtanulni” a LaTeX-et? Miért nehéz „megtanulni” a LaTeX-et?

Ezzel elérkeztünk a fekete leveshez. A LaTeX oly korban készült program, amikor még nem volt egér, ezért mindent a billentyűzetről kell elérni, és mindent, de tényleg mindent, amit a programtól kérni akarunk, parancs formájában be kell gépelnünk. Ezért egyrészt rengeteget kellett gépelni (a szövegen kívül), másrészt ismerni kellett azokat a parancsokat, amelyekkel rávehetjük a programot a szöveg megfelelő formázására (például arra, hogy zárjon középre egy szöveget vagy tegyen dőltbe egy szöveget). Régebben sokakat eltántorított ez a TeX használatától, de ma már sok szövegszerkesztő segíti ezt a munkát, és ez sok terhet levehet a vállunkról.

És még egy nagy hátránya van: mivel a formázásra szolgáló utasítások — amelyek maguk is szövegek — bele vannak írva a szövegbe, nem azt látjuk a képernyőn, amit valójában meg akarunk jeleníteni, hanem egyszerre szöveget és utasításokat, a programot időről-időre meg kell kérni, hogy legyen szíves mutassa meg, hogy mindez hogyan fog majd kinézni (állítsa össze a kiadványt). Ez a lépés kihagyhatatlan. Nincs olyan ember, aki hosszú oldalakon keresztül képes hibátlanul beírni az utasításokat, és közben fejben elképzelni, hogy az hogyan fog kinézni. Akinek ez nehézséget okoz, több olyan szövegszerkesztő is készült a LaTeX-hez, amely a beírással lényegében egyidőben mutatja is (gyakorlatilag folyamatosan befordítja), milyen lesz a kész dokumentum.

Ettől persze még tudnunk kell, mit csinálunk, hogyan szedjük a szöveget, vagyis a LaTeX-et csak ésszel lehet használni.

És akkor mégis miért?

Mert mindenért kárpótol minket az, hogy ami elkészül, az valami parádés lesz!

Akkor vágjunk bele!

Mint említettem, ha van egy jól telepített rendszerünk, akkor az első élményünk gyors, látványos és lenyűgöző lesz.

Mivel sokféle rendszer van, és más-más rendszerre más és más a telepítés módja, csak a legelterjedtebb rendszerre (windows) történő telepítést írom le részletesebben. (Más rendszerekben, például Linux alatt a TeXlive, Macintosh alatt a MacTeX programot lehet használni.)

Az általam alább javasolt programok mindegyike ingyenes, a telepítése meglehetősen egyszerű, de csak a hivatalos oldalról szabad telepíteni őket. A problémák elkerülése érdekében érdemes ezeket oda telepíteni, ahova a rendszer felkínálja. Szükségünk lesz egy PDF nézegető programra, egy TeX rendszerre és egy szövegszerkesztőre. Én csak egy-egy lehetőséget adok meg, mindegyik helyett lehet mást választani.

A telepítés részletei:

1. PDF nézegető program: Javaslom a Sumatra PDF®-et. A legelterjedtebb, az Acrobat Reader® beállításaival gondok lehetnek.

2. TeX rendszer: MikTeX®. A program telepítéskor rákérdez, hogy a későbbiekben telepítheti-e a hiányzó csomagokat. Ezt érdemes megengedni.

3. Szövegszerkesző: TeXnicCenter®. (Mást is választhatunk, de ez ingyenes, és nagyon sok szolgáltatása van. Az igazsághoz azonban hozzátartozik, hogy maga a MikTeX is tartalmaz egy szövegszerkesztőt, a TeXworksöt. Ez ugyan kevésbé felhasználóbarát, de a TeX rendszer hibáit automatikusan javítja.) A TeXnicCenter telepítés után rákérdez, hogy konfigurálja-e a szövegszerkesztőt. Érdemes ezt rögtön megtenni. Megkérdezi, hogy hol találja meg a ps nézegető programot. Itt meg kell adni a pdf nézegető program könyvtárát. Ezután a menük alatti sávban középtájt egy fehér hátterű mezőben megjelenik, hogy milyen fordítási opciókat lehet kérni. Válasszuk ki a LaTeX  $ \Rightarrow$ PDF opciót.

Teszt:

Mindennél fontosabb, hogy ellenőrizzük, jól működik-e a rendszer. Kezdjünk új üres TeX fájlt, és írjuk be a következő néhány sort:

\documentclass{article}
\begin{document}
x
\end{document}

Bizonyosodjunk meg róla, hogy egyetlen betűt sem írtunk el. (Az egész fájlban az egyetlen szöveg az x. Minden más csak a LaTeX-nek szóló utasítás, parancs.)

Mentsük le a fájlt, majd nyomjuk meg a Ctrl+F7 billentyűzetkombinációt.

Ha mindent jól csináltunk, alul egy kis ablakban üzen nekünk a program, és végül ezt írja:

LaTeX-Result: 0 Error(s), 0 Warning(s), 0 Bad Box(es), 1 Page(s)

BibTeX-Result: 0 Error(s), 0 Warning(s)

Ha hibátlanul írtuk be a szöveget, de mégsem ez történik, akkor hibás a MikTeX vagy a telepítés. Ha a telepítés hibás, azon csak egy újratelepítés segít, ha a MikTeX hibás, akkor keresni kell a honlapon egy korábbi verziót, és azt telepíteni.

Ezután megtekinthejük az alkotásunkat, az F5 gomb hatására megjelenik a PDF nézegető program. (Ha nem nyitja meg a PDF-et, akkor gond van. Lehet, hogy az AcroRd okozza a gondot. Ezen az a kényelmetlen, de áthidaló megoldás segíthet, ha a PDF-et kézzel megnyitjuk.)

A PDF-en egy x betűt és egy 1-es számot látunk. Az 1 oldalszám, ezt automatikusan tette bele a program. Az x helyére szinte bármit beírhatunk. Ha azonban ékezetes szöveget írunk be, kellemetlen meglepetésben lehet részünk.

Ékezetes betűk

A szövegszerkesztő alsó kék sávjában a közepétől jobbra ANSI vagy UTF-8 felirat látható. Ez azt mutatja meg, hogy milyen ékezetes kódolást használ a szövegszerkesztő. Ezzel összhangba kell hozni azt, hogy a LaTeX milyen kódolást használjon.

Érdemesebb az UTF-8 kódolást használni, mert sokoldalúbb, mint az ANSI.

Előrször adjuk meg a LaTeX-nek, hogy UTF-8 kódolást akarunk használni. Írjuk be az 1. és a 2. sor közé (új 2. sorba):

\usepackage[utf8]{inputenc}

Ha a szövegszerkesztő is UTF-8-ra van állítva, akkor azzal nincs más dolgunk. Ha azonban ANSI-ra van állítva, mentsük a fájlunkat másként (Save As), és a megnyíló párbeszédablakban a kódolást (Encoding) állítsuk át UTF-8-ra (igen, írjuk felül). Ezzel a szövegszerkesztőt összhangba hoztuk a LaTeX-hel.

Beírunk valamilyen ékezetes szöveget, és ismét befordítjuk a LaTeX-et PDF-be: Ctrl+F7, majd ha nem kaptunk hibajelzést, akkor F5-tel megnézzük a PDF-et.

Speciális karakterek

1. Mivel a programnak meg kell tudnia különböztetni a parancsokat a szövegtől, lefoglalt egy karaktert, amelyet arra használ, hogy a parancsok azzal kezdődjenek, ez pedig a \ karakter. Minden szó, ami ezzel kezdődik, a TeX-nek szóló parancs. Ez egyrészt azt jelenti, hogy ha ezt lefelejtjük, akkor nem a parancs, hanem az azt követő szöveg kerül bele, másrészt meg azt, hogy ezt a karaktert nem tudjuk a billentyűzetről karakterként beírni.

Arra is figyelnünk kell, hogy a parancs után szóközt (vagy más, nem betű karaktert) kell írni, hogy a TeX tudja, hogy véget ért a parancs. A TeX hibák jelentős része az ilyen parancsok hibás beírásából ered.

Ám más speciális karaktert is használ a TeX, amelyekről érdemes tudni.

2. A \ után a legfontosabb, { és } karaktereket (csoportosító vagy csoport vagy group karakterek) arra használja a TeX, hogy körülhatárolja azt a szöveget, amelyre a parancs vonatkozik. A használata kissé ellentmondásos, mert egyes esetekben a parancsot a kapcsos zárójeleken belülre kell írni, más esetekben pedig a nyitó kapcsos zárójel elé. Az a ritkább, hogy belülre kell írni, de érdemes odafigyelni, hogyan kell használni.

3. A szóköz és a soremelés nem különösebben speciális, de fontos megjegyezni néhány dolgot. Akárhány szóközt is írunk be, abból csak egyetlen szóköz lesz (amelynek a méretét a tördelés, vagyis a program határozza meg). Ráadásul matematikai képleten belül hiába írunk be szóközt, azt nem veszi tekintetbe a rendszer. A billentyűzet TAB karaktere is csak egy szóközt eredményez. De a TAB és a szóköz együtt is csak egyetlen szóközt ad. Ennél meglepőbb, hogy az a billentyű, amely arra szolgál, hogy új sort kezdjünk (soremelés billentyű, amelyre RETURN vagy ENTER van írva, vagy csak egy visszafelé — kocsi vissza — nyíl van rárajzolva) is csak egy szóközt fog eredményezni.

Jogosan merül fel tehát a kérdés, hogy akkor hogyan lehet új sort kezdeni.

Új sort nem kezdhetünk, csak új bekezdést. Ehhez két soremelést kell beírni. (Megjegyzem, hogy elvileg lehet új sort kezdeni, de el sem mondom, hogyan lehet elérni, mert tipográfiailag elképesztően súlyos hiba. El kell tudni dönteni, hogy új bekezdést akarunk-e kezdeni, vagy nem. Ha nem, akkor ne erőszakoskodjunk a TeX-hel.)

A soremelés billentyűvel is ugyanaz a helyzet, mint a szóközzel: akárhányszor nyomjuk is le (legalább kétszer), ugyanannyi lesz két bekezdés között a távolság.

Természetesen jól el tudom képzelni, hogy valakinek nem tetszik a TeX által felkínált formátum. De ne feledkezzünk meg róla, hogy a tipográfiának, a kiadványok előállításának szigorú szabályai vannak, és a TeX ezeknek — alapesetben — eleget tesz. Ezért addig, amíg nem ismerjük elég jól a tipográfiát és a TeX-et, ne állítsuk át az alapbeállításokat.

4. További speciális karakterek:

— Gondolatjel: beírása két kötőjellel történik: --.

% Ha egy sorba százalékjelet teszünk, akkor az azt követő karaktereket a TeX nem veszi tekintetbe. Így a sor végén álló (szóközként funkcionáló) soremelés karaktert sem.

$ A dollár jel segítségével matematikai képletet lehet beírni.

_ Az aláhúzás karakterrel indexet írhatunk. A TeX-nek meg kell mondani, hogy mi kerül az indexbe. Az indexben szereplő jeleket csoportosító karakterek közé kell tenni.

^ A kalap karakterrel kitevőt írhatunk. Meg kell mondani, hogy mi kerül a kitevőbe. A kitevőbe kerülő jeleket csoportosító karakterek közé kell tenni.

& A latin et jelét arra használhatjuk, hogy elválasszunk táblázatba vagy táblázatos elrendezésbe (mint például egy mátrix) kerülő objektumokat.

~ A hullám (tilde) karakter el nem törhető szóközt jelent a TeX-ben.

" A macskaköröm jelet ne használjuk.

Érdemes egy nagy levegőt venni, és kipróbálni az eddigieket

A dokumentum elejére írjuk be a következő sorokat (egyelőre magyarázat nélkül):

\documentclass[12pt]{article}
\usepackage[utf8]{inputenc}
\usepackage[magyar]{babel}
\usepackage{amsmath,amssymb,amsfonts,amsthm}
\frenchspacing

Ez a dokumentum bevezető része, ebben állítjuk be, hogy milyen csomagokat akarunk használni. Ezt a részt preambulumnak is szokás nevezni.

Ezután következik a tényleges dokumentum (ami messze nem jelenti azt, hogy többet nem üzenünk már semmit a LaTeX-nek). Az első sora \begin{document}, az utolsó \end{document}

Írjunk be egy tetszőleges szöveget — egyelőre olyat, amelyben nincsen matematika.

Játsszunk el kicsit a szöveg formátumával is!

Tegyünk bele kiemelés gyanánt dőlt betűs szövegeket, például \textit{dőlt}, illetve félkövér (ez egy nyomdai szakkifejezés, ami azt jelenti, hogy vastagabb betűs) szövegeket, például \textbf{félkövér}.

Arra azonban vigyázzunk, hogy a félkövér szöveg nagyon tolakodó, ezért ne írjunk vele hosszas szövegrészeket, kizárólag egy-egy szót, azt is csak indokolt esetben.

A \begin{center} és \end{center} parancsok közé írt sorokat a LaTeX középre zárja.

Például az alábbi mintaszöveg (amelyhez felhasználtuk a debreceni egyetem honlapján található ismertetőt):

Elindult az Érintő — Elektronikus Matematikai Lapok, a Bolyai János Matematikai Társulat kiadásában. A negyedévente megjelenő online folyóirat rovataiban ismeretterjesztő írások olvashatók a matematika tanításáról, tudományos eredményeiről, ipari és pénzügyi alkalmazásairól.

Az olvasáshoz jó szórakozást kívánunk!

így írható be:

Elindult az \textbf{Érintő} -- Elektronikus Matematikai Lapok, a Bolyai János Matematikai Társulat kiadásában.
A negyedévente megjelenő \textit{online} folyóirat rovataiban ismeretterjesztő írások olvashatók
a matematika tanításáról, tudományos eredményeiről, ipari és pénzügyi alkalmazásairól.

\begin{center}
Az olvasáshoz jó szórakozást kívánunk!
\end{center}

A matematika szöveg fontos része: a képlet

Azt tapasztaltam, hogy sokaknak nehéz eldönteni, hogy mi matematika és mi nem. Pedig ez a TeX használatához nagyon fontos, mert egészen másképp néz ki egy képlet, mint a folyószöveg.

Talán úgy lehetne legegyszerűbben megfogalmazni, hogy a képlet olyan matematikai kifejezés, amelyet szöveg vesz közre, és amelyben általában nincs szöveg.

Például abban a szövegben, hogy „Pitagorasz tétele szerint egy $ a,b,c$ oldalú derékszögű háromszögben, ahol $ c$ az átfogó, fennáll, hogy $ a^{2}+b^{2}=c^{2}$.” képlet az $ a,b,c$, a $ c$ és az $ a^{2}+b^{2}=c^{2}$ kifejezés.

Így írjuk be:

Pitagorasz tétele szerint egy $a,b,c$ oldalú derékszögű háromszögben, ahol $c$ az átfogó, fennáll, hogy $a^{2}+b^{2}=c^{2}$.

Képlet beírása TeX-ben

A TeX-ben a képletet két $ jel közé tesszük (LaTeX-ben lehet még másképp is, de az hosszasabb).

Például: $6+3=9$ eredménye $ 6+3=9$, $a+b=c$ eredménye $ a+b=c$.

Látható, hogy a képletben szereplő betűket a TeX automatikusan dőltté teszi. Nemcsak a betűket, hanem minden más karaktert a képlet tördelési szabályainak megfelelően ír.

Ahhoz, hogy megértsük, hogy miért úgy néz ki a képlet a TeX-ben, ahogy kinéz, meg kell ismernünk néhány alapvető tipográfiai szabályt.

A képlet részei:

Számok, változónevek, műveleti és relációs jelek, zárójelek, függvénynevek, operátornevek, egyéb matematikai jelek.

A pozíciójuk lehet normál, index, index indexe, kitevő, kitevő kitevője, index kitevője, kitevő indexe (stb.)

Az önmagukban álló számokat csak akkor kell képletként írni, ha azok matematikai tartalmat hordoznak ($ 14$ osztható $ 7$-tel). A nem matematikai tartalmú számokat soha. Például: 1962-ben. A helyesírás szabályai szerint a kis számokat — amennyiben nem hordoznak matematikai tartalmat — amúgy is betűkkel kell kiírni: Hófehérke és a hét törpe.

A számok betűtípusa szövegben és képletben (rendszerint) megegyezik.

A változónevek rendszerint dőlt betűsek, ám a szöveges dőlt betű típusa eltér a képlet dőlt betűjétől. Ezért a változóneveket csak képletként írhatjuk be, a TeX automatikusan dőltté teszi a változóneveket.

A vektorokat félkövér betűkkel kell beírni (a tipográfiai szabvány szerint). Például $ \mathbf{v}(1;2)$ írásmódja $\mathbf{v}(1;2)$

Itt is láthatjuk, hogy a képletben szereplő félkövér betűt (a vektor \mathbf) nem úgy kell beírni, mint a szövegben szereplőt (\textbf).

Műveleti és relációs jelek

Műveleti jelek pl. $ +$, $ -$, $ \cdot$ (írásmódja: \cdot), $ \pm$ (írásmódja: \pm)

A tört írásmódja: \frac{}{} (az első kapcsos zárójelbe a számlálót, a másodikba a nevezőt kell írni). Például: $\frac{2a}{b}$ eredménye $ \frac{2a}{b}$.

Relációs jelek pl. $ =$ $ \ne$ $ >$ $ <$ $ \ge$ $ \le$ $ \geqq$ $ \leqq$ $ \approx$
beírásuk: =, \ne, \neq > < \ge, \geq \le, \leq \geqq \leqq \approx

Zárójelek

A matematikában többféle zárójelet, zárójelpárt használunk: (, ), [, ], $ \{$, $ \}$. Ezek közül az első négyet el lehet érni a billentyűzetről. Ám a kapcsos zárójelek a TeX speciális karakterei, így ha a billentyűzetkaraktereket írjuk be, akkor azokból nem zárójelek lesznek, hanem a TeX-nek szóló üzenetek. A kapcsos zárójeleket így írhatjuk be: \{ és \} (és csak matematikai módban használjuk).

A zárójelek méretének a közrefogott képlet méretéhez kell igazodniuk. Ezt automatikusan úgy érhetjük el, hogy a bal oldali zárójel elé azt írjuk:\left, a jobb oldali elé azt:\right

Például 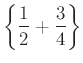$ \left\{\dfrac12+\dfrac34\right\}$ írásmódja: $\left\{\frac{1}{2}+\frac{3}{4}\right\}$.

A TeX függvénynevek használata

A tipográfia szabályai szerint a matematikai függvények betűje álló. Nem írhatjuk például azt, hogy $sin x$, mert az így jelenne meg: $ sin x$. (Még a szóköz is eltűnt!)

A függvényeket TeX parancsként kell beírni: \sin, \sin x.

Néhány gyakori függvény:

\max                  \min                  \lim                   
\sup                  \inf                  \limsup                  \liminf
\exp                  \log                  \lg                  \ln

tg és ctg nincs, azt definiálnunk kell. Érdemes a preambulumban, a \begin{document} elé:

\newcommand\tg{\operatorname{tg}}

\newcommand\ctg{\operatorname{ctg}}

A leggyakoribb TeX operátorok

$ \leq$      \leq $ \geq$      \geq $ \neq$      \neq
$ \approx$      \approx $ \times$      \times $ \vdots$      \vdots
$ \pm$, $ \mp$      \pm, \mp $ \cdot$      \cdot $ {}^{\circ}$      {}^{\circ}
$ \circ$      \circ $ {}^\prime$      ' $ \ldots$      \ldots
$ \infty$      \infty $ \neg$      \neg $ \wedge$      \wedge
$ \vee$      \vee $ \supset$      \supset $ \forall$      \forall
$ \in$      \in $ \rightarrow$      \rightarrow $ \subset$      \subset
$ \exists$      \exists $ \notin$      \notin $ \to$      \to
$ \Rightarrow$      \Rightarrow $ \Leftarrow$      \Leftarrow $ \mapsto$      \mapsto
$ \Leftrightarrow$      \Leftrightarrow $ \leftrightarrow$      \leftrightarrow $ \mid$      \mid
$ \cup$      \cup $ \cap$      \cap $ \setminus$      \setminus
$ \hat{}$      \hat{} $ \bar{}$      \bar{} $ \tilde{}$      \tilde{}

A $ \{\ \}$ azt jelenti, hogy argumentumot vesz fel, arra illeszti a TeX a megfelelő jelet.

A leggyakoribb görög betűk

$ \alpha$          \alpha                  $ \beta $          \beta                  $ \gamma$          \gamma
$ \delta$          \delta                  $ \epsilon$          \epsilon                  $ \varepsilon$          \varepsilon
$ \zeta$          \zeta                  $ \eta$          \eta                  $ \theta$          \theta
$ \vartheta$          \vartheta                  $ \iota$          \iota                  $ \kappa$          \kappa
$ \varkappa$          \varkappa                  $ \lambda$          \lambda                  $ \mu$          \mu
$ \nu$          \nu                  $ \xi$          \xi                  $ \pi$          \pi
$ \rho$          \rho                  $ \varrho$          \varrho                  $ \sigma$          \sigma
$ \tau$          \tau                  $ \upsilon$          \upsilon                  $ \phi$          \phi
$ \varphi$          \varphi                  $ \chi$          \chi                  $ \psi$          \psi
$ \omega$          \omega                  $ \Gamma$          \Gamma                  $ \Delta$          \Delta
$ \Theta$          \Theta                  $ \Lambda$          \Lambda                  $ \Xi$          \Xi
$ \Pi$          \Pi                  $ \Sigma$          \Sigma                  $ \Upsilon$          \Upsilon
$ \Phi$          \Phi                  $ \Psi$          \Psi                  $ \Omega$          \Omega

Néhány további fontos TeX parancs

Határérték \lim_{n\to \infty} $ \lim\nolimits_{n\to \infty}$
vagy \lim\limits_{n\to \infty} $ \lim\limits_{n\to \infty}$
szumma \sum_{k=1}^{n} $ \sum\nolimits_{k=1}^{n}$
vagy \sum\limits_{k=1}^{n} $ \sum\limits_{k=1}^{n}$
produktum \prod_{k=1}^{n} $ \prod\nolimits_{k=1}^{n}$
vagy \prod\limits_{k=1}^{n} $ \prod\limits_{k=1}^{n}$
integrál \int_{0}^{t}, \int\limits_{0}^{t} $ \int_0^t$, $ \int\limits_0^t$
négyzetgyök \sqrt{ } $ \sqrt{\quad}$
$ k$-adik gyök \root{k}\of{ }, \sqrt[k]{ } $ \root{k}\of{\quad}$, $ \sqrt[k]{\quad}$

Hasonló — mégis más, ne tévesszük össze!

$ \backslash$ ($ \backslash$backslash), nincs matematikai funkciója $ \setminus$ ($ \backslash$setminus), halmazkivonás, pl. $ A\setminus B$
$ \colon$ ($ \backslash$colon), függvénydefiníció, halmazdefiníció, pl. $ f\colon x\to 1$, $ \{x\colon x<0,x\in\mathbb{Z}\}$ $ :$ (:), osztás, arány, pl. $ a:b$
$ \vert$ ($ \backslash$vert vagy |), abszolút érték, pl. $ 2\vert x\vert y$ $ \mid$ ($ \backslash$mid), osztó, halmazelválasztó, pl. $ x\mid y$, $ \{x\mid x\in\mathbb{R}, x<0\}$
$ \Vert$ ($ \backslash$Vert vagy $ \backslash$|), norma, pl. $ \Vert A\Vert$ $ \parallel$ ($ \backslash$parallel), párhuzamos, pl. $ A\parallel B$
$ \Sigma$, görög betű $ \sum$, szumma jel
$ \Pi$, görög betű $ \prod$, produktum jel

Index és kitevő

Az index írása az _{ } jellel történik (a kapcsos zárójelbe az indexet kell írni). Például: $3a_{2k+1}$ eredménye $ 3a_{2k+1}$.

A kitevő írása a ^{ } jellel történik (a kapcsos zárójelbe a kitevőt kell írni). Például: $10^{10}$ eredménye $ 10^{10}$.

Példa: $3x_{5}^{12}+12y_{12}^{5}$ eredménye $ 3x_{5}^{12}+12y_{12}^{5}$.

Ha csak egy karakter van a kapcsos zárójeleken belül, akkor a zárójel elhagyható, de ez számos hiba forrása lehet.

A TeXnicCenter zölddel jelöli azokat a zárójeleket, amelyeknek megtalálja a párját, pirossal azokat, amelyeknek nem. Érdemes ezt is figyelni!

A tizedesvessző írása

A képletben beírt vesszőt a TeX úgy tekinti, hogy a felsorolás elválasztó karaktere, ezért helyet tesz utána. Ezt úgy lehet kiköszöbölni, hogy a tizedesvesszőt kapcsos zárójelek közé tesszük: $ 4{,}2$ írásmódja $4{,}2$. Ha lemarad a kapcsos zárójel, akkor $ 4,2$ lesz belőle, mintha felsorolás lenne.

Mivel a tizedestört matematikai kifejezés, mindig képletként kell beírni.

Nézzünk néhány példát

A másodfokú egyenlet megoldóképletét így írhatjuk be:

Az $ ax^2+bx+c=0$ ($ a\ne 0$) másodfokú egyenlet megoldásai $ x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.

Az $ax^2+bx+c=0$ ($a\ne 0$) másodfokú egyenlet megoldásai
$x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.

Vegyük észre, hogy mi került egy-egy képletbe. A kikötés egy új képlet, amelynek a nyitó és záró zárójele nem része a képletnek, tehát szöveges, maga a kikötés matematikai kifejezés.

A szinusztétel:

Ha egy háromszög három oldalát $ a$, $ b$ és $ c$ jelöli, a velük szemközti szögeket pedig rendre $ \alpha$, $ \beta $ és $ \gamma$, akkor fennáll, hogy $ a:b:c=\sin\alpha:\sin\beta:\sin\gamma$.

Ha egy háromszög három oldalát $a$, $b$ és $c$ jelöli,
a velük szemközti szögeket pedig rendre $\alpha$, $\beta$ és $\gamma$,
akkor fennáll, hogy $a:b:c=\sin\alpha:\sin\beta:\sin\gamma$.

Kiemelt, középrezárt képlet

Előfordulhat, hogy egy képletet kiemelve, középre zárva akarunk beírni. Ezt úgy tehetjük meg, hogy nem egy-egy, hanem két-két dollárjel közé zárjuk a képletet. Ez ugyan nem a legjobb megoldás (majd látunk rá sokkal jobbat), de egyelőre maradjunk ennyiben.

Például

Az $ ax^2+bx+c=0$ ($ a\ne 0$) másodfokú egyenlet megoldásai

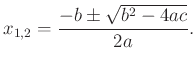
$\displaystyle x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}. $

 

Az $ax^2+bx+c=0$ ($a\ne 0$) másodfokú egyenlet megoldásai
$$
x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.
$$

Erről a következőkben sokkal több szót ejtünk.

Ismét vegyünk nagy levegőt, és tegyük próbára a TeX-et

Ezúttal válasszunk egy olyan szöveget, amely tartalmaz matematikát, és próbáljuk meg beírni.

Gyakorlati tanácsok:

1. Tartsuk magunk előtt (a képernyőn vagy kinyomtatva) a relációs jelek, a leggyakoribb TeX függvények, TeX operátorok, a leggyakoribb görög betűk, a további TeX parancsok és a Hasonló — mégis más táblázatokat.

2. Figyeljük, hogy fordításkor jelez-e hibát a program. Ha igen, azonnal keressük meg. Eleinte gyakran fordítsuk be a LaTeX-et PDF-re, hogy ha hibát jelez a program, akkor tudjuk, hol keressük.

A leggyakoribb hibák forrása: lemarad a $ \backslash$ a parancs elől, betűelírás a parancsban, lemarad egy nyitó vagy záró kapcsos zárójel, nem kapcsos zárójelet írunk oda, ahova azt kellett volna, lemarad egy $ jel.

3. A legelső hibát keressük meg, mert lehet, hogy az okoz további 50 hibát. A TeX a hibaüzeneteket a hibát tartalmazó sor számával együtt adja meg, így könnyen megtaláljuk a hibát tartalmazó sort. A szövegszerkesztő segít: a felső sorban található piros háromszög ikonra kattintva ráugrik a hibás sorra. (A View menüpontban állítsuk be, hogy a szövegszerkesztő jelezze a szövegben a sorszámot, Ctrl+Shift+F7 billentyűzetkombináció).

4. Ha nem találjuk meg a hibát, akkor zárjuk le a dokumentumot \end{document} egy korábbi sornál, ahol még — reményeink szerint — nem lehet hiba. Ezek után tegyük egyre hátrább és hátrább a dokumentum lezáró sorát. Ha még mindig nem találjuk a hibás sort, akkor egyesével tegyük % jel mögé a gyanús sort, sorokat.

5. Ha úgy tűnik, hogy minden rendben van, de mégis hibát jelez a program, akkor a fordítás során létrejövő állományok közül töröljük azokat, amelyekre nincs szükségünk, legfőképpen az aux kiterjesztésűt. Lehet ugyanis, hogy valamilyen hiba egy korábbi fordítás során ezekbe bekerülve továbbra is hibát eredményez.

6. Ha ez sem segít, akkor ellenőrizzük, hogy egy korábban jól működő TeX még mindig jól működik-e. Ha most hibás, akkor a rendszerrel történhetett valami. Ha a korábbi fájl hibátlan, akkor sajnos mégis hiba van a mostani fájlban. Ilyenkor csak a türelem segít, előbb-utóbb megtaláljuk a hibát.

 

FOLYT. KÖV.

 Fried Katalin

informatika TeX - LaTeX