A geometriában az egyik legtermészetesebb kérdés, hogy két pont között melyik a legrövidebb út. Igaz-e, hogy két pont között a legrövidebb az egyenes?
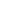
A válasz az euklideszi síkon vagy térben természetesen igen, ha úgy definiáljuk az „egyenest”, hogy az a távolságot minimalizáló görbe. Ekkor a minimalizáló „egyenes” tényleg az egyenes. De az is természetes, hogy vannak olyan esetek, amikor a távolságot minimalizáló görbe nem az egyenes. Például a gömbfelületen, ahol a minimalizáló görbék körívek lesznek. Nem is akármilyen körívek, hanem az úgynevezett főkörívek, amelyek sugara a gömb sugarával egyezik meg. Itt egyébként egy érdekes jelenséggel is találkozhatunk: az egy pontból kiinduló széttartó „egyenesek” széttartása lelassul és egy idő után elkezdenek összetartani. Ez egy jellemző tulajdonsága a pozitív görbületű felületeknek. Ez a viselkedés pontosan az ellentéte az úgynevezett negatív görbületű felületeknek, ahol az „egyenesek” széttartása növekszik:
Pozitív, nulla és negatív görbületű felületek [1]
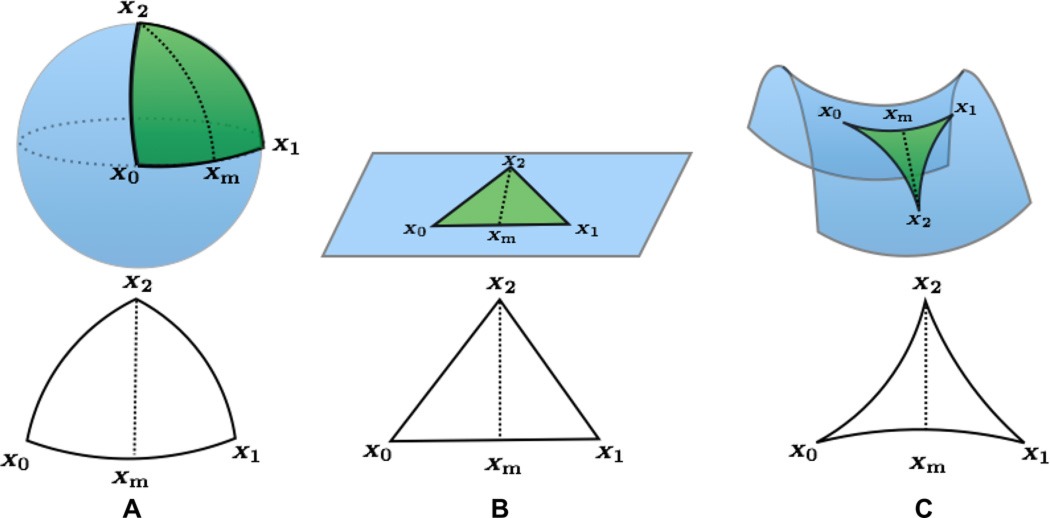
A fenti ábra A és C példájában az alapul vett felület eleve görbült volt, így a rajta haladó „egyeneseknek” is görbülniük kellett. De el tudunk-e képzelni egy olyan világot, ahol az alapul vett tér lapos, mégis az „egyenesek” nem egyenesek, hanem görbe vonalak? Képzeljük el, hogy a világegyetem egy lapos körlap! A körlap szélén rendkívül hideg van (abszolút nulla fok), a közepén viszont meleg. Jelentősen eltúlozva vegyük figyelembe a hőtágulást: a körlap széle felé haladva a testek mérete a lehűléssel tartson a nullához. Mi lesz az optimális stratégia, ha az A pontból át szeretnénk menni a B pontba?
 Természetesen az egyenes vonalon átmehetünk egyik pontból a másikba, de ez azzal jár, hogy végig a hideg területen gyalogolunk. Megmutatható, hogy hamarabb átérünk A-ból B-be, ha A-ból először a világunk melegebb belseje felé vesszük az irányt és így folyamatosan felmelegedve és kitágulva B pont felé kanyarodunk. Érdekességként megjegyezzük, hogy az egy pontból kiinduló „egyenesek” széttartása gyorsul, ami azt jelenti, hogy az így kapott tér görbülete negatív. A megfelelő hőtágulási viszonyokat beállítva ebben a térben a Bolyai János által felfedezett hiperbolikus geometria világa lesz érvényes.
Természetesen az egyenes vonalon átmehetünk egyik pontból a másikba, de ez azzal jár, hogy végig a hideg területen gyalogolunk. Megmutatható, hogy hamarabb átérünk A-ból B-be, ha A-ból először a világunk melegebb belseje felé vesszük az irányt és így folyamatosan felmelegedve és kitágulva B pont felé kanyarodunk. Érdekességként megjegyezzük, hogy az egy pontból kiinduló „egyenesek” széttartása gyorsul, ami azt jelenti, hogy az így kapott tér görbülete negatív. A megfelelő hőtágulási viszonyokat beállítva ebben a térben a Bolyai János által felfedezett hiperbolikus geometria világa lesz érvényes.
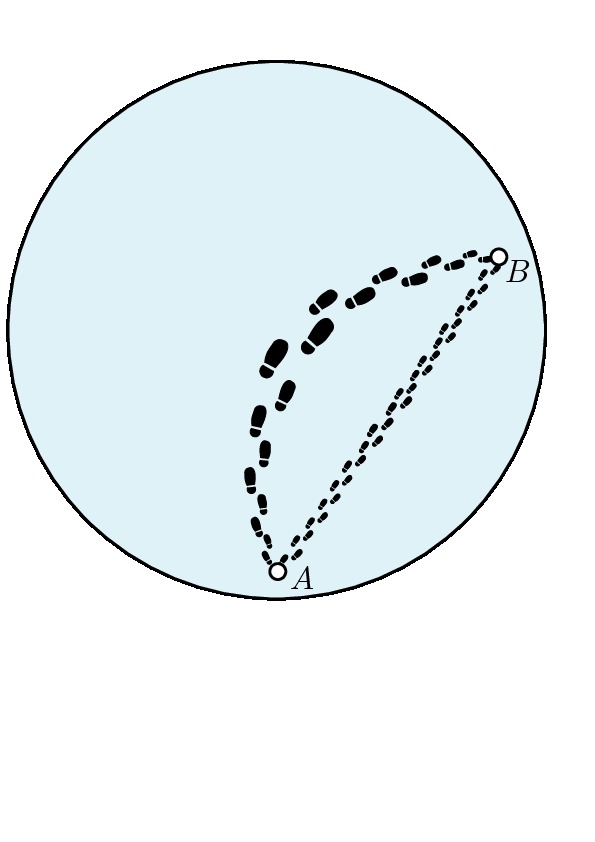
A fenti példa egy fontos tényre világít rá: az „egyenesek” viselkedése, és így a tér geometriai jellege (görbülete) megváltozhat azzal, ha a távolságmérés megváltozik. Az előző példában ugyanis pontosan ez történt: egységnyi idő alatt más-más távolságra juthatunk el attól függően, hogy milyen irányban indultunk. Ilyen jelenségre számos példát találhatunk a gyakorlati életben. A cikk apropója Fa Nándor kiváló sportteljesítménye a Vendée Globe földkerülő vitorlás versenyen. A rendkívül nehéz fizikai igénybevétel mellett a verseny nehézsége többek között abból áll, hogy meg kell tervezni az optimális útvonalat úgy, hogy a szél alapvetően befolyásolja a távolságmérést (adott pontokban az időegység alatt elérhető pontok halmazát), és így a tér geometriáját. Az eredmény egy igen bonyolult tér, amelynek azonban kiterjedt szakirodalma van (Zermelo navigációs probléma, Randers-típusú Finsler-terek elmélete).
Vendée Globe 2016–2017: Fa Nándor útvonala [2,3]
A geometriai görbület fogalmával érdekes módon a tudomány sok egyéb területén is találkozhatunk. Természetes módon jelenik meg a fizikában, csillagászatban, de találkozhatunk alkalmazásokkal a földrajz, biológia és a közgazdaságtan területén is.
Aki szeretne többet megtudni a cikkben szereplő geometriákról, annak ajánljuk Lánczos Kornél [4] könyvét, illetve az [5] és [6] cikkeket.
Muzsnay Zoltán
Irodalomjegyzék
- 1
- Sandhu, R. S., Georgiou, T. T., Tannenbaum, A. R.: Ricci curvature: An economic indicator for market fragility and systemic risk, Sci. Adv. 27, 2016: Vol. 2, no. 5, e1501495
- 2
- Fa Nándor honlapja: http://spiritofhungary.hu
- 3
- Vendée Globe földkerülő vitorlás verseny honlapja: http://www.vendeeglobe.org/
- 4
- Lánczos K.: A geometriai térfogalom fejlődése: A geometriai fogalmak fejlődése Püthagorasztól Hilbertig és Einsteinig, Budapest, Typotex, 2010
- 5
- Hiperbolikus geometria: https://hu.wikipedia.org/wiki/Hiperbolikus_geometria
- 6
- Zermelo navigációs problémája: https://en.wikipedia.org/wiki/Zermelo's_navigation_problem
A bevezető kép készítője Fa Nándor indulásáról a Vendée Globe versenyén Eric Houdas, forrása: https://commons.wikimedia.org/wiki/Category:N%C3%A1ndor_Fa#/media/File:Nandor_Fa_(8).jpg