A differenciaegyenletek csodálatos világa

Számtalan alkalommal tapasztalhatjuk, mind az oktatás, mind a tudományos kutatás területén, hogy a folytonos idejű modellek sokkal nagyobb hangsúllyal jelennek meg, mint a diszkrét rendszerek. Ennek oka alapvetően az, hogy általában az előbbiek segítségével szeretnénk a természet különféle jelenségeit leírni és megérteni. Azonban – ahogyan azt Kovács Sándor Differenciaegyenletek (Typotex, 2020) című könyvének előszavában is olvashatjuk – az alkalmazott és elméleti matematika bizonyos területein gyakran előbukkannak a differenciaegyenletek is. Ezért érdemes e rendszerek elméletében is elmélyülnie mindazoknak, akiknek tanulmányai vagy tudományos érdeklődése valamilyen módon kötődik a matematikához.

A könyv ismertetése előtt ízelítőként egy közismert példával szeretném illusztrálni, hogy mekkora különbségek lehetnek a differenciál- és a differenciaegyenletek, vagy alkalmazott szemlélettel fogalmazva, a folytonos és a diszkrét idejű modellek között. Tekintsük az

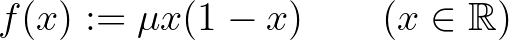
$\displaystyle f(x) := \mu x(1-x) \qquad (x \in \mathbb{R})$

logisztikus leképezést, valamint az 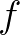$f$ jobb oldalú differenciál- illetve differenciaegyenletet:

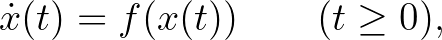
$\displaystyle \dot{x}(t) = f(x(t)) \qquad (t \geq 0),$

$\displaystyle (\Delta x)_{n} = f(x_n) \qquad (n \in \{0,1,\ldots\}),$

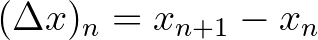$(\Delta x)_{n} =x_{n+1}-x_n$ az (előrefelé vett) differenciaoperátor. Ismeretes, hogy a folytonos idejű egyenlet megoldása valamely 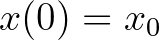$x(0)=x_0$ kezdeti feltétel mellett

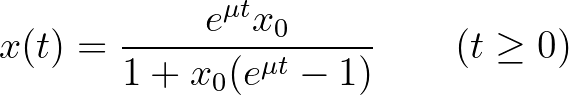
$\displaystyle x(t)= \displaystyle \frac{e^{\mu t} x_0}{1+x_0(e^{\mu t}-1)} \qquad (t \geq 0)$

és az egyenlet 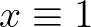$x \equiv 1$ egyensúlyi megoldása globálisan aszimptotikusan stabilis, így a differenciálegyenlet bizonyos értelemben „szép”, „jól kiszámítható”. Az egyenlet 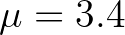$\mu=3.4$ paraméterérték és $x_0 \in [0,2]$ kezdeti feltételek melletti megoldásai az 1. ábrán láthatók.

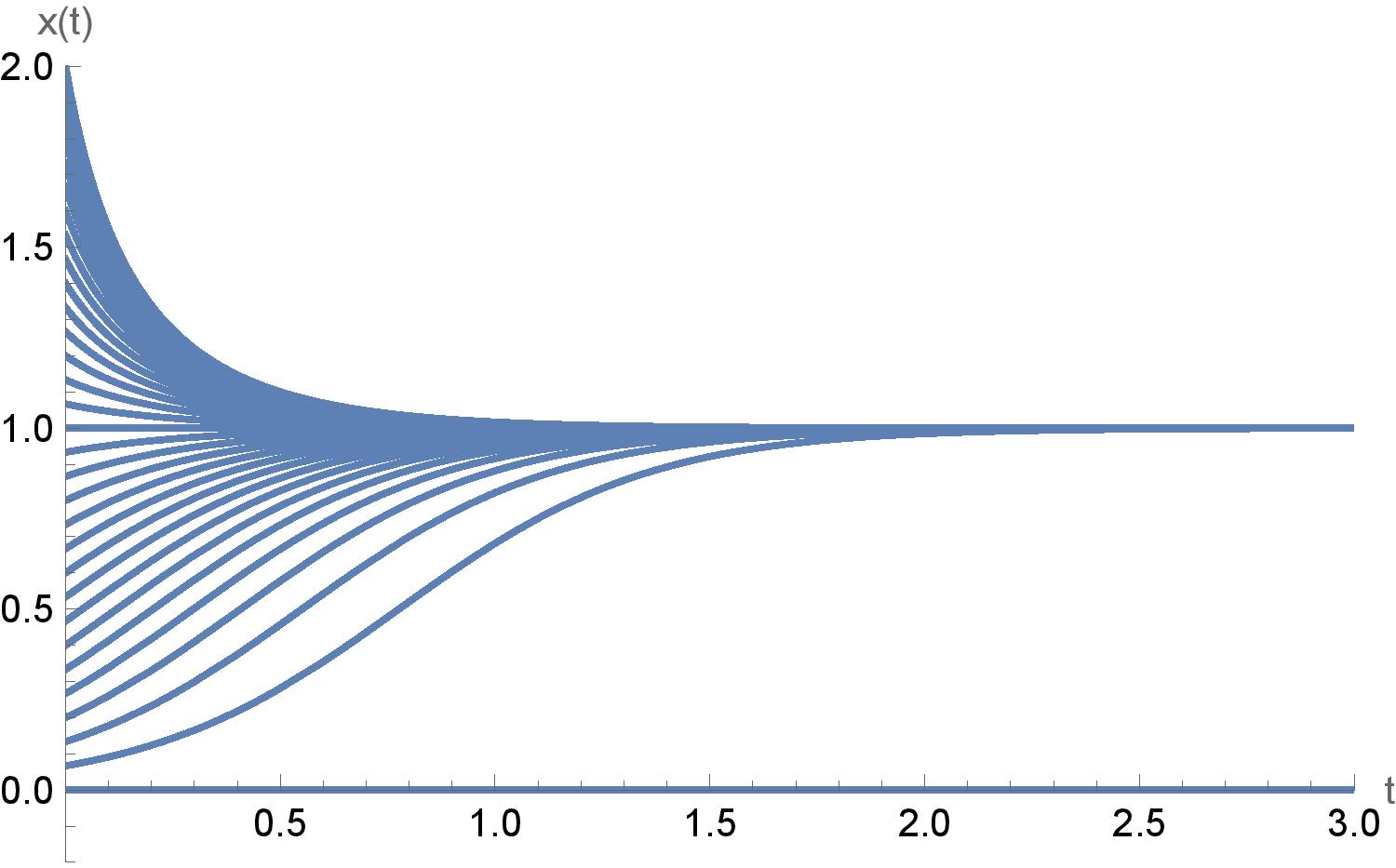
1. ábra. A folytonos idejű egyenlet megoldásai.

Ezzel szemben a diszkrét idejű egyenlet változatos viselkedést mutat. Kis paraméterértékek esetén itt is megfigyelhető a pozitív egyensúlyi helyzet globális stabilitása, de a paraméter értékének növelésével hosszú idő után periodikus pályák jelennek meg, sőt, a periódusok hossza a paraméter további növelésével megduplázódik, azaz először egy 2-periódusú pálya jelenik meg, mely aszimptotikusan stabilis elegendően nagy paraméterérték esetén, majd a stabilitást egy 4-periódusú pálya veszi át, ezt követően egy 8-periódusú aszimptotikusan stabilis pálya tűnik fel a színen, és így tovább. Ez az ún. perióduskettőződés jelensége, amely tulajdonképpen bifurkációk sorozata, és amelynek vizsgálatával az 1970-es években több híres kutató is foglalkozott (vö. [1], [2], [3], utóbbi magyar fordítása: [4]). Az egyenlet közismert bifurkációs diagramja látható a 2. ábrán.

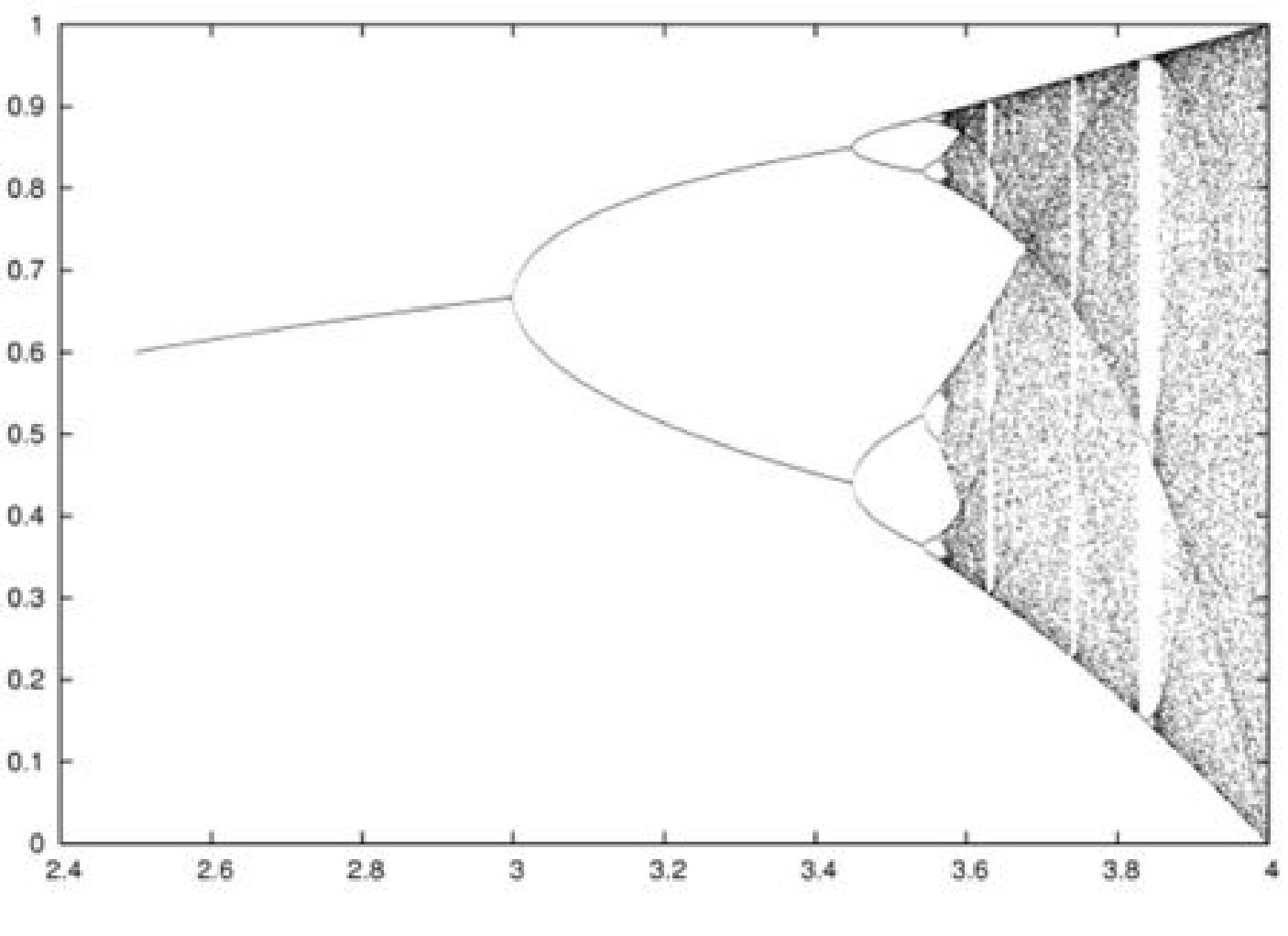
2. ábra. A diszkrét logisztikus egyenlet bifurkációs diagramja $\mu \in [0, 4]$ paraméterértékek esetén.

Ez már önmagában nagyon izgalmas és szembetűnő különbség a folytonos és diszkrét idejű egyenletek között, azonban a diszkrét változatban a 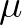$\mu$ paraméter értékének további növelésével az egyenlet kaotikussá válik, ami tulajdonképpen a folytonos idejű egyenletnél megfigyelt „rendezettség” ellentétének is tekinthető.

Természetesen a fenti, példaként felmerülő folytonos modellből kiindulva tévesen lehetne arra következtetni, hogy a differenciálegyenletek elmélete egyszerű és izgalmaktól mentes terület lenne, hiszen ezen típusú rendszerekben is rengeteg érdekes és figyelemreméltó viselkedést figyeltek már meg a kutatók, azt pedig nem is tudhatjuk, mit tartogatnak számunkra a még felfedezetlen tulajdonságok. Azt hiszem, hogy ezen a ponton meg kell emlékeznünk nemrég elhunyt kollégánkról, Besenyei Ádámról, aki rengeteg hallgatóval ismertette meg „A differenciálegyenletek csodálatos világát”.

Mindezek után térjünk át a Differenciaegyenletek című kötet rövid ismertetésére.

A jegyzet anyagán erőteljesen érződik, hogy a szerző aktív egyetemi oktató: Kovács Sándor nagymértékben épített több éves – a BME-n és az ELTE-n szerzett – gyakorlati tapasztalataira, amelyet a kötetben található feladatok (illetve a hozzájuk tartozó részletes megoldási útmutató) jelentős száma és a logikus, jól áttekinthető, mondhatjuk, „hallgatóbarát” felépítés is tükröz. Az olvasó számára nagy segítség továbbá a könyvhöz csatolt Függelék is, amelyben a szerző részletesen bemutatja az egyes fejezetekhez szükséges alapvető ismereteket, fogalmakat.

Az első fejezetben a diszkrét operátorkalkulus alapvető fogalmait és állításait mutatja be a szerző, amelyek ismerete szinte nélkülözhetetlen a továbbiak megértéséhez. Bár a képletek és matematikai formulák mennyisége elsőre ijesztő lehet a kevésbé elméleti irányultságú olvasónak, a kidolgozott példák és feladatok nagy segítséget nyújtanak a fejezetben tárgyalt ismeretek elsajátításához. A klasszikus analízis kedvelőinek külön figyelmébe ajánlható a „Klasszikus tételek diszkrét változata” című alfejezet, melyben többek között a közismert Rolle-tétel, valamint a Lagrange- és Cauchy-féle középértéktétel diszkrét változata is olvasható.

A könyv második szakaszában a szerző 13 példán keresztül illusztrálja, miként jelennek meg a diszkrét dinamikai rendszerek különböző alkalmazott és elméleti matematikai problémákban, jól oldva ezzel az első fejezet tömörségét (az elméleti alapok megértésében kevésbé motivált olvasónak lehet, hogy érdemes ezzel a fejezettel kezdeni a könyv tanulmányozását). Szó esik például a jól ismert „Hanoi tornyai” elnevezésű feladatról, de betekintést kapunk differenciálegyenletek megoldásának hatványsoros módszerébe is, mellyel kiszámíthatók például az ún. Airy-féle differenciálegyenlet megoldásai. A fejezet második felében a diszkrét dinamikai rendszerekhez kapcsolódó alapvető fogalmakat ismerhetjük meg.

3. ábra. A Hanoi tornyai elnevezésű játék 8 koronggal. A legenda szerint a játék feltalálása (64 koronggal) Buddha nevéhez fűződik. (Forrás: Wikipédia)

A harmadik fejezet a lineáris differenciaegyenletekkel foglalkozik, rendre bemutatja az első-, másod-, valamint magasabb rendű lineáris differenciaegyenleteket, végül a lineáris differenciaegyenlet-rendszereket is. Valamennyi rész esetében külön-külön vizsgálja a változó és állandó együtthatós egyenletek alakját és megoldási módszereit. Ebben a fejezetben is nagy hangsúlyt kapnak az alkalmazások: az első- és másodrendű egyenletek általános bevezetése után néhány, többnyire az alkalmazott matematikából származó problémán keresztül szemlélteti a szerző az adott típusú egyenletekkel kapcsolatos elméleti eredményeket. Például a kamatos kamat számításának klasszikus problémája mellett olvashatunk változó kamatlábat feltételező modellről, bepillantást nyerhetünk az áramkörök működésének elméletébe, végül az ún. tönkremenési probléma kapcsán felmerülő peremérték-feladatot is górcső alá vesszük. További hasznos segítség, hogy bizonyos feladatokhoz Mathematica nyelven írt kód is tartozik, amelyekkel az adott feladat megoldásai szemléltethetők.

A lineáris egyenletek után néhány speciális alakú nemlineáris differenciaegyenlet szerepel a könyv 4. fejezetében. Majd az ezt követő utolsó szakaszban a lineáris és nemlineáris egyenletekben fellépő stabilitási fogalmat boncolgatja a szerző, mellyel az egyenletek megoldásainak aszimptotikus viselkedését vizsgálhatjuk. A fent bemutatott logisztikus egyenletek kapcsán már láthattuk, hogy ezek a tulajdonságok mennyire izgalmasak és változatosak. Az előzőekhez hasonlóan itt is néhány alkalmazással zárja a sort a szerző, ahol többek között a könyv korábbi példáiban bemutatott egyenletek stabilitását vizsgálja.

Ahogy az a fent leírtakból is jól látható, a bemutatott mű teljes mértékben követi az egyetemi jegyzeteknél szokásos klasszikus felépítést (a tételek részletes bizonyítása, feladatok kitűzése, a megoldások leírása, valamint az elméleti tudnivalók illusztrálása példákon keresztül), ebből adódóan sok munkát vár el olvasójától. Ám e struktúra egyben rengeteg segítséget is nyújt a szerző vállalt céljának eléréséhez, vagyis ahhoz, hogy megismertesse és megértesse a differenciaegyenletek elméletének alapjait. Összefoglalva, a kötet remek választás mind hallgatók, mind kutatók és oktatók számára, hogy saját ismereteiket bővítsék, vagy éppen izgalmas diplomamunka-témák után kutakodjanak.

Irodalomjegyzék

: [1] Feigenbaum, M. J. Universality in complex discrete dynamics. Los Alamos Theoretical Division Annual Report 1975–1976 (1976).

[2] Metropolis, N., Stein, M. L., Stein, P. R. On Finite Limit Sets for Transformations on the Unit Interval. Journal of Combinatorial Theory (A) 15, 25–44 (1973).

[3] May, Robert M. Simple mathematical models with very complicated dynamics. Nature 261, 459-467 (1976).

[4] May, Robert M. Nagyon bonyolult dinamikájú egyszerű matematikai modellek. (fordította Turányi Tamás) Alkalmazott Matematikai Lapok 8, 427-446 (1982).

György Szilvia

ELTE Informatikai Kar