Bevezetés a valószínűségszámításba

David F. Anderson, Timo Seppäläinen, Benedek Valkó: Introduction to Probability

A címben szereplő bevezetés (introduction) szót nagyon komolyan kell venni. A könyv célja az, hogy bemutassa a valószínűségszámítás alapjait, és legfontosabb, nehéz matematikai apparátust nem igénylő eredményeit. A szerzők fontosnak tartották, hogy ne csak az eredmények bizonyítását ismertessék, hanem bőséges példaanyag segítségével érzékeltessék azok hasznosságát is, és egyben megtanítsák a valószínűségszámítás néhány fontos módszerének az alkalmazását.  Ez a könyv elsősorban az amerikai egyetemeken szereplő bevezető valószínűségi kurzusok számára készült. Különböző nehézségű feladatokat tartalmaz, jelezve közülük a nehezebb, több munkát igénylőket, lehetőséget adva arra, hogy az oktatók az általuk vezetett kurzus diákjainak a tudásához, képességeihez igazítsák az oktatást.

A könyv megértéséhez az olvasónak rendelkeznie kell alapvető analízisismeretekkel, viszont nem szükséges hozzá a mértékelmélet mélyebb eredményeinek az ismerete. A szerzők olyanokkal is meg akarták ismertetni a valószínűségszámítást, akik nem tanultak mértékelméletet. Itt egy komoly problémába ütközünk, aminek a megértéséhez érdemes egy kis történelmi utalást tenni.

Általában úgy tekintik, hogy a valószínűségszámítás a 17. század közepén alakult ki Blaise Pascal és Pierre de Fermat levelezése során. Ők ebben a levelezésben de Méré lovag szerencsejátékokkal kapcsolatos kérdéseit tárgyalták meg. Bár később is születtek fontos valószínűségszámítási eredmények, a modern, mai valószínűségszámítás elméletét Andrej Nyikolajevics Kolmogorov dolgozta ki Grundbegriffe der Wahrscheinlichkeitsrechnung (A valószínűségszámítás alapfogalmai) című 1933-ban megjelent könyvében. (Magyarul: Gondolat, 1982; Typotex, 2010.) A valószínűségszámítás megjelenése és annak precíz megalapozása között tehát majdnem 300 év telt el. Ennek az az oka, hogy bár a valószínűségszámítás problémáinak megértéséhez nem kellenek komoly matematikai ismeretek, azok precíz tárgyalásához a modern matematika egy fontos részének, a mértékelméletnek az alkalmazása szükséges. Ez komoly gondot jelent akkor, ha olyan majdani alkalmazóknak akarjuk elmagyarázni a valószínűségszámítás lényegét, akik nem tanultak mértékelméletet. Ezzel a nehézséggel szembesültek az itt ismertetett könyv szerzői is.

Ők úgy oldották meg ezt a problémát, hogy egyrészt kerülték az olyan túlságosan bonyolult és elvont fogalmak és kérdések tárgyalását, amilyenekkel a valószínűségszámítást gyakorlati problémák megoldásában alkalmazók nem fognak találkozni. Másrészt bizonyos eredményeket, amelyek bizonyítása komoly matematikai apparátust igényelt volna, bizonyítás nélkül közöltek. Jelen ismertetés írója egyetért ezzel a hozzáállással, de van néhány olyan pont, ahol vitatkozna a szerzőkkel. Erről az ismertetés későbbi részében lesz szó.

A könyv 10 fejezetből és egy appendixből áll. Az appendix a könyvben felhasznált legfontosabb analízisbeli és kombinatorikai eredményeket tárgyalja, valamint megadja néhány valószínűségi eloszlás táblázatát.

Az első fejezet ismerteti a valószínűségszámítás néhány alapvető fogalmát, a valószínűségi mérték (eloszlás), a véletlen esemény, valamint a valószínűségi változó definicióját, tárgyalja ezek legfontosabb tulajdonságait, és több példa megoldását ismerteti. Ezek segítik az itt bevezetett fogalmak jobb megértését.

E fejezetben a valószínűségi változó bevezetése érdemel külön figyelmet, ami eltér e fogalom hagyományos tárgyalásától. A szerzők először bevezetik a mintatér (sample space) fogalmát, és ezen definiálják a valószínűségi eloszlásokat és valószínűségi változókat. Mint a bevezetőben írják, ez fontos annak érdekében, hogy elkerüljék azt az érzést, hogy a valószínűségi változó egy homályos fogalom. Ezen ismertetés írója nem ért egyet ezzel a hozzáállással, mivel így néhány fontos kérdésnek hiányzik a megfelelő magyarázata. E probléma tárgyalása az ismertetés későbbi részeiben is meg fog jelenni.

A második fejezet néhány, a véletlen eseményekkel kapcsolatos fogalmat és eredményt tartalmaz. Bevezeti a feltételes eloszlást, események, majd valószínűségi változók függetlenségének a fogalmát, bebizonyít néhány ezekkel a fogalmakkal kapcsolatos eredményt, és tárgyalja a Bayes-formulát.

A harmadik fejezet témája a valószínűségi változók fogalma. Bevezeti az eloszlás és az eloszlásfüggvény fogalmát, (amit a könyv cumulative distribution function-nak nevez), majd tárgyalja a várható értéknek és szórásnégyzetnek a valószínűségszámításban rendkívül fontos fogalmát, illetve megmutatja, hogyan lehet ezeket kiszámolni. Csak a diszkrét eloszlású és a sűrűségfüggvénnyel rendelkező valószínűségi változók függvényeinek a kiszámítására ad a könyv képletet, de ez a megszorítás elfogadható, mert a gyakorlatban csak ilyen valószínűségi változókkal találkozunk. Bevezet néhány fontos eloszlást, így a binomiális, a geometriai eloszlásokat, a normális eloszlást, és kiszámítja az ilyen eloszlású valószínűségi változók várható értékét és szórásnégyzetét. Viszont hiányzik a várható érték egy rendkívül fontos tulajdonságának az említése. Nevezetesen az, hogy valószínűségi változók összegének a várható értéke egyenlő az egyes valószínűségi változók várható értékének az összegével. Pontosabban, ez az eredmény csak a könyv végén, a nyolcadik fejezetben jelenik meg, és ott is csak speciális esetekben bizonyítva.

Ez a hiány összefügg azzal, hogy a valószínűségi változók ebben a könyvben csak a mintatereken vannak definiálva. Ha általános terekben definiáljuk azokat, akkor a várható érték additivitása következik az integrálok jól ismert additivitásából. Természetesen a dolog nem ilyen egyszerű. Az általános (és a valószínűségszámítás legtöbb tárgyalása során bevezetett) várható érték definíciója esetén meg kell magyarázni, hogy az általános esetben miért és hogyan tudjuk a problémáinkat a mintatereken definiált valószínűségi változókkal és azok eloszlásaival való számolással megoldani. Ehhez ismertetni kell a mértékelmélet néhány alapvető eredményét. Mégis, véleményem szerint ez a helyes tárgyalásmód. Ugyanis ezeknek az eredményeknek a bemutatása nem annyira nehéz, viszont így érthetőbb és teljesebb képet kapunk a valószínűségszámítás néhány problémájáról.

A könyv egyik célja az, hogy az olvasó megismerje a legfontosabb valószínűségszámítási törvényeket. Először olyan speciális esetekben tárgyalja ezeket a törvényeket, amelyekben a bizonyítás egyszerűbb. Ez a negyedik fejezet fő témája. Ez a fejezet először a binomiális eloszlással foglalkozik, bebizonyítja erre a centrális hatéreloszlástételt a Stirling-formula segítségével, majd a nagy számok törvényét is, de ezt is csak a binomiális eloszlás esetében. Tárgyal néhány érdekes feladatot, például azt, hogy hogyan lehet bizonyos statisztikai problémákban konfidenciaintervallumot szerkeszteni a centrális határeloszlás-tétel segítségével. Ez a matematikai statisztika egyik fontos feladata.

Ezután a könyv bevezeti a Poisson-eloszlást, és megadja a binomiális eloszlás jó közelítését Poisson-eloszlás segítségével. A fejezet következő témája az exponenciális eloszlás, és annak legfontosabb tulajdonságai. Végül bevezeti a Poisson-folyamat definícióját, és definiálja segítségével a gamma-eloszlást. Hiányolom ebből a tárgyalásból annak a bizonyítását, hogy a Poisson-folyamat valóban létezik, azaz létezik olyan sztochasztikus folyamat, amely teljesíti a Poisson-folyamat definíciójában szereplő feltételeket.

Az ötödik fejezet ismert eloszlású valószínűségi változók függvényeit tekinti, és ezek várható értékének, illetve eloszlásának a kiszámolásával foglalkozik. Az úgynevezett momentumgeneráló függvénynek a kiszámolása és tulajdonságainak a vizsgálata e fejezet fő témája. Egy 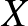valószínűségi változó momentumgeneráló függvénye az 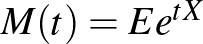függvény, ahol 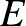várható értéket jelöl, és a 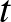paraméter egy valós szám. A fejezet megfogalmazza a momentumgeneráló függvény néhány fontos tulajdonságát. Például azt, hogy egy valószínűségi változó momentumgeneráló függvényének az értéke az origó egy kis környezetében meghatározza a valószínűségi változó eloszlását. A szerzők azért foglalkoznak a momentumgeneráló függvényekkel és azok tulajdonságaival, mert ezek segítségével fogják belátni a centrális határeloszlás-tételt.

A hatodik fejezet az ötödik fejezet természetes folytatása. Itt azt a problémát tárgyalják, hogy amennyiben ismerjük több valószínűségi változó együttes eloszlását, akkor hogyan tudjuk kiszámolni ezen valószínűségi változók valamely függvényének a várható értékét és eloszlását. Először azzal az esettel foglalkoznak, amikor a valószínűségi változók mindegyike diszkrét eloszlású. Ez viszonylag egyszerű probléma, a könyv korábbi fejezeteiben felhasznált módszerek segítségével tárgyalható. A könyv bemutatja az ezzel kapcsolatos legfontosabb eredményeket, és bevezeti az úgynevezett polinomiális eloszlásokat, amelyek természetes módon megjelennek e vizsgálatok során.

A következő vizsgálandó eset az, amikor az egyes valószínűségi változók folytonos eloszlásúak, azaz sűrűségfüggvénnyel rendelkeznek. A könyv módszerei csak azon speciális eset vizsgálatához elegendőek, ahol ezek a valószínűségi változók együttesen is folytonosak, azaz az együttes eloszlásuknak van (többváltozós) sűrűségfüggvénye. Ezekről bizonyít be a könyv eredményeket. Ezek közül a legfontosabb az, amelyik megadja sűrűségfüggvényekkel rendelkező valószínűségi változók függetlenségének a jellemzését a sűrűségfüggvények segítségével. A fejezet több példát is tartalmaz. Többek között bevezeti a kétváltozós standard normális eloszlást. (Ez olyan 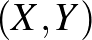véletlen vektor eloszlása, amelynek a koordinátái független, standard normális eloszlású valószínűségi változók.)

A hetedik fejezet fő témája a konvolúció. Ez egy olyan operátor, amelynek segítségével ki tudjuk számolni ismert eloszlású független valószínűségi változók összegének az eloszlásfüggvényét valamint sűrűségfüggvényét is, feltéve, hogy az utóbbi létezik. E fejezet több példát tárgyal a konvolúció alkalmazásáról. Például megmutatja, hogy független, normális eloszlású valószínűségi változók összege olyan normális eloszlású valószínűségi változó, amelynek várható értéke, illetve szórásnégyzete megegyezik az összeadandók várható értékének, illetve szórásnégyzetének az összegével. Ez tanulságos háttérinformáció a később tárgyalt centrális határeloszlás-tételhez.

Ezután ez a fejezet foglalkozik az úgynevezett felcserélhető valószínűségi változókkal, és megmutatja, hogy ezek néhány egyszerűen bizonyítható tulajdonsága nagy segítséget nyújt bizonyos feladatok megoldásában. Például tekinthetjük a következő feladatot. Egy urnában különböző színű golyók vannak, és minden szín esetén tudjuk, hogy hány ilyen színű golyó van az urnában. Visszatevés nélkül kihúzunk golyókat, mindegyik golyót egyforma valószínűséggel. Mi a valószínűsége, hogy bizonyos húzásoknál (például az ötödik, hetedik és tizedik húzásnál) előírt színű golyót húzunk? Ez a feladat nagyon egyszerűvé válik, ha ismerjük a szükséges eredményeket a felcserélhető valószínűségi változókról.

A hetedik fejezet utolsó témája a Poisson-folyamat egy fontos tulajdonságának az ismertetése, tudniillik annak, hogy egy Poisson-folyamat egymást követő pontjai közötti távolságok egymástól független exponenciális eloszlású valószínűségi változók.

A nyolcadik fejezet első eredménye a várható érték additivitásáról szól. Ezt bizonyítja bizonyos speciális esetekben. Erről az eredményről már volt szó a harmadik fejezetről szóló részben is. A könyv több olyan példát is tárgyal, ahol ez az állítás jól használható. A második fontos, ebben a fejezetben tárgyalt állítás, hogy független valószínűségi változók szorzatának a várható értéke megegyezik az egyes valószínűségi változók várható értékének a szorzatával. Fontos megjegyezni, hogy ez a szorzat várható értékéről szóló eredmény, ellentétben a megfelelő összegekről szólóval, csak független valószínűségi változók esetében érvényes. A könyv egyszerű bizonyítást ad erre abban az esetben, ha az egyes valószínűségi változók diszkrét eloszlásúak vagy sűrűségfüggvénnyel rendelkeznek. (A könyv csak ilyen eseteket tárgyal.) A bizonyítás azon alapszik, hogy valószínűségi változók függetlensége jó jellemezhető  sűrűségfüggvényeik segítségével.

A fejezet több példát is megad, ahol ezek az eredmények hasznos összefüggésekre mutatnak rá. Így például egyszerű képlet van arra, hogy független valószínűségi változók összegének ne csak a várható értékét, hanem a szórásnégyzetét is kiszámolhassuk. Ugyancsak hasznos alkalmazás bizonyos eloszlások, például a negatív binomiális eloszlás, a binomiális eloszlás várható értékének és szórásnégyzetének a kiszámítása. A fejezet külön tárgyalja ezek segítségével a híres kupongyűjtő problémát, ami a következőképp szól: Egy cég a termékeit egy dobozban árulja, és mindegyik dobozba betesz ráadásként egy játékdarabot. A játékdaraboknak összesen 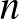különböző típusa van, és minden dobozba egymástól függetlenül ugyanolyan valószínűséggel helyezik el ezen játéktípusok valamelyikét. Ha valaki összegyűjti az összes játéktípust, akkor jutalmat kap. Hány dobozt kell vásárolnunk ahhoz, hogy elnyerjük ezt a jutalmat? A szerzők kiszámolják a nyeréshez szükséges dobozszám várható értékét és szórásnégyzetét. E feladat külön érdekessége, hogy ahhoz, hogy összegyűjtsük a játéktípusok felét, várhatólag kevesebb dobozt kell vásárolnunk, mint ahhoz, hogy megszerezzük azt az utolsó, még hiányzó játéktípust.

E fejezet megmutatja az előző eredmények segítségével, hogy független valószínűségi változók összegének a momentumgeneráló függvénye egyenlő az egyes függvények momentumgeneráló függvényének a szorzatával. Megmutatja ennek az állításnak az alkalmazását is néhány példában. De ez az eredmény igazán a következő fejezetben tárgyalt centrális határeloszlás-tétel bizonyításában bizonyul hasznosnak.

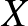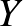Ezután ebben a fejezetben bevezetik a kovariancia és a korreláció fogalmát. Az és valószínűségi változó

kovarianciafüggvénye valamilyen értelemben ezen valószínűségi változók egymás közötti függését méri, és ennek ismeretében ki tudjuk számolni valószínűségi változók összegének a szórásnégyzetét akkor is, ha azok nem függetlenek. A korrelációfüggvény a kovarianciafüggvény alkalmas normalizáltja. A nyolcadik fejezet felsorolja a kovarianciafüggvény legfontosabb tulajdonságait. Végül ebben a fejezetben bevezetik először a kétváltozós majd az általánosabb többváltozós normális eloszlás fogalmát. Ezen ismertetés írója itt hiányolja néhány tény tárgyalását.

Helyesnek tartottam volna, ha a könyv ismertette volna a következő fejezetben a centrális határeloszlás-tétel mellett annak többdimenziós változatát is. Ez tette volna érthetőbbé, miért vezették be a többdimenziós normális eloszlásokat. Ezek a többdimenziós centrális határeloszlás limeszeként jelennek meg a valószínűségszámításban.

Ez magyarázatot adott volna arra is, hogy miért fontos definiálni a többdimenziós normális eloszlást abban az esetben is, ha annak nincs sűrűségfüggvénye. Vannak fontos példák, amikor a többdimenziós centrális határeloszlás-tétel limesze ilyen eloszlás. Mint a könyv megjegyzi, ilyen esetekben is lehet definiálni a többdimenziós normális eloszlást, például annak momentumgeneráló függvénye segítségével.

A kilencedik fejezet ismerteti a klasszikus valószínűségszámítás legfontosabb eredményeit. Először a Markov- és Csebisev-egyenlőtlenséget bizonyítja. A fejezet következő témája a nagy számok törvénye. Ez a következőt állítja: Vegyük független, egyforma eloszású 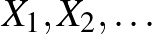valószínűségi változók 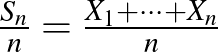átlagát minden 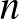számra. Ezek az átlagok nagyon enyhe és természetes feltételek mellett konvergálnak ezen valószínűségi változók 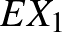várható értékéhez, ha az 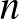szám tart a végtelenhez. A fenti állítás pontos megfogalmazásához szükséges tisztázni azt is, hogy hogyan definiáljuk ezen átlagok konvergenciáját, azaz be kell vezetni egy alkalmas konvergenciafogalmat a valószínűségi változók terében. Kétfajta konvergenciát szoktak tekinteni. Az egyik az úgynevezett sztochasztikus konvergencia. Ha az átlagok sztochaszikusan konvergálnak, akkor a nagy számok gyenge törvényéről beszélünk. Egy erősebb, úgynevezett majdnem mindenütt konvergencia teljesülését a nagy számok erős törvényének nevezik. A könyv mind a kétfajta konvergencia teljesülését bebizonyítja alkalmas feltételek mellett. Ugyanakkor ezek a feltételek lényegesen gyengíthetők, de ennek bizonyításához a könyvben nem tárgyalt módszerek szükségesek.

A kilencedik fejezet következő témája a valószínűségszámítás talán legfontosabb eredménye, a centrális határeloszlás-tétel. Ez a következő állítást fogalmazza meg. Tekintsük független valószínűségi változók egy végtelen sorozatát, és minden pozitív egész 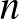számra vegyük e sorozat első 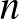tagjának az összegét, és annak normalizáltját. (A normalizálás során az összegből kivonjuk annak várható értékét, majd elosztjuk a szórásával.) Ezen normalizált összegeknek az eloszlása nagyon általános feltételek mellett konvergál a standard normális eloszláshoz, ha 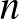tart végtelenhez.

A könyv csak független, egyforma eloszlású valószínűségi változók normalizált összegeivel foglalkozik. A momentumgeneráló függvények segítségével bizonyítja be ezt az eredményt, igaz a szükségesnél erősebb feltételek mellett.  A szerzők megfogalmazzák az éles változatot is, és megjegyzik, hogy ennek az éles változatnak a bizonyítása nagyon hasonló az általuk ismertetett bizonyításhoz. Ez azonban csak részben igaz. Az éles eredményt valóban a könyvben ismertetettekhez nagyon hasonló számolások segítségével kaphatjuk meg, ha a momentumgeneráló függvények helyett azok egy alkalmas módosításával, az úgynevezett karakterisztikus függvényekkel számolunk. De a bizonyításnak van egy másik része is. Meg kell indokolni, hogy az elvégzett számolásokból miért következik a centrális határeloszlás-tétel. És ez az indoklás ebben az új esetben már más módszereket igényel.

Ez a fejezet megemlíti a kapott eredmények néhány érdekes alkalmazását. Ezek egyike az úgynevezett Monte Carlo-módszer, ami lehetőséget ad bizonyos nehezen számolható mennyiségek (például bonyolult integrálok) viszonylag pontos kiszámítására megfelelő eloszlású véletlen minták segítségével. A könyv ismertet példákat, amikor ez a módszer jól alkalmazható.

A könyv utolsó, tizedik fejezete a feltételes valószínűség és feltételes várható érték fogalmát tárgyalja az általános esetben. Ez egy meglehetősen kényes téma, amitől sokan idegenkednek. Szemléletesen a feltételes várható érték jelentése a következő. Van egy véletlen, azaz valószínűségi változó. Ennek várható értéke azt fejezi ki, hogy mit várunk, ennek értéke (bizonyos hibával) körülbelül mekkora lesz. De ha vannak plusz ismereteink, amelyek befolyásolják e változó értékét, akkor azokat is figyelembe vesszük, amikor azt becsüljük meg, hogy mit várunk. Ezt próbáljuk kifejezni a feltételes várható érték bevezetésével. De ha a valószínűségi mező felbomlik kontinuum sok nulla valószínűségű diszjunkt esemény uniójára, és azt tudjuk, hogy ezen nulla valószínűségű események közül melyik következett be, akkor nehéz megmondani, hogy ezt az információt hogyan kell figyelembe venni.

Az általános esetben ezt a feltételes valószínűséget és várható értéket a mértékelmélet egy mély eredményének, az úgynevezett Radon–Nikodym-tételnek és az e tételben bevezetett Radon–Nikodym-deriváltnak a segítségével definiálják. Ezzel a Radon–Nikodym-deriválttal elég nehéz számolni, és ezért sokan igyekeznek ezt elkerülni.

A könyv szerzői úgy kerülik el ezt a nehézséget, hogy csak abban az esetben dolgoznak ezekkel a fogalmakkal, amikor a tekintett valószínűségi változók diszkrét eloszlásúak, vagy létezik együttes sűrűségfüggvényük. Mind a két esetben definiálják természetes módon a feltételes sűrűségfüggvényt, majd ezek segítségével definiálják, szintén természetes módon, a feltételes valószínűséget és feltételes várható értéket. Bebízonyítanak néhány eredményt a feltételes várható értékről. Ezek között van olyan, a feltételes várható érték bizonyos optimum tulajdonságát kifejező állítás is, ami jelzi, hogy miért játszik a feltételes várható érték fontos szerepet a statisztikai becslések elméletében.

Ez a tárgyalás segíthet a feltételes valószínűség és várható érték fogalmának a megértésében az általános esetben, amikor nulla mértékű feltételekkel is tudnunk kell dolgozni. A könyv ad néhány útmutatást arról, hogy mit kell tenni az általános esetben, de ez nem elegendő a felmerülő nehézségek leküzdéséhez.

Röviden összefoglalva, ezen ismertetés írójának a következő a véleménye: Ez a könyv hasznos lehet azok számára, akik a valószínűségszámítás alkalmazásával foglalkoznak, szeretnének valamilyen képet kapni arról, hogy mivel foglalkozik ez a tudomány, de nem kívánnak elmélyült tanulmányokat folytatni. Viszont azoknak, akik a valószínűségszámítás elméletét mélyebben meg kívánják ismerni, és hajlandóak több energiát fordítani arra, hogy megtanulják az ehhez szükséges elméletet, más könyveket érdemes tanulmányozni.