A tér alakja

Jeffrey R. Weeks: A tér alakja (Felületek és háromdimenziós alakzatok ábrázolása)

Mielőtt az említett könyv rövid ismertetésére rátérnék, megemlíteném, hogy Weeks professzorral személyesen is találkoztam, és egy nagytudású, több nyelven beszélő, a kultúra más területein is nagyon tájékozott, szerény embert ismertem meg benne. A 2002. évi Bolyai 200 Emlékkonferencia meghívott előadója volt. Emlékezetes előadást tartott, és cikket is írt az emlékkötetbe (Non-Euclidean Geometries, János Bolyai Memorial Volume, Editors: András Prékopa and Emil Molnár, Springer 2006). Munkásságával kapcsolatban itt csak azt említeném meg, hogy 1985-ben szerezte Ph.D. fokozatát a Princeton University-n William Thurston témavezetésével. Nevéhez fűződik a nevezetes Weeks-féle sokaság (Fomenko-Matveev-Weeks-sokaság), amely a legkisebb térfogatú zárt irányítható hiperbolikus háromsokaság.

A tér alakjában Jeffrey R. Weeks két- és háromdimenziós terek geometriáját és topológiáját vizsgálja; elsősorban a terek szerkezeteinek szemléletes képeit mutatja be. Nem követi a geometria és a topológia sok előtanulmányt megkövetelő szigorú felépítését, de alaposan körüljárja a terek megismeréséhez és leírásához kapcsolódó fogalmakat, és rendkívül intuitív módon, ábrák, példák és kitűzött gyakorlatok segítségével vezeti el az olvasót azok megismeréséhez.

A könyv nem sorolható be a „könnyű népszerüsítő munkák” közé, de nem is tankönyv, talán úgy fogalmazható meg legjobban, hogy kedvet csinál ahhoz, hogy a terek topológiáját és geometriai szerkezetét jobban megismerjük. De tekintsük át röviden a könyv felépítését:

1. Az I. rész (Felületek és háromsokaságok): A fejezet E. A. Abbott Síkföld című munkájának (amely angolul letölthető innen, magyarul meg innen, és amelyet mindenkinek ajánlok gondolatébresztőnek) alapgondolatával kezdődik, és annak továbbfejlesztésével eljut a felületek (kétdimenziós sokaságok), illetve analógia alapján a háromdimenziós sokaságok fogalmához. Majd következnek az ezek felépítéséhez, elemzéséhez és megértéséhez kapcsolódó kulcsfontosságú fogalmak: mi a geometria és topológia, mik a belső és külső tulajdonságok, melyek a globális és lokális tulajdonságok, mik a homogén és inhomogén geometriák, mitől zárt és nyílt egy sokaság, mi az irányíthatóság, mi az összefüggő egyesítés fogalma, mi a lapos sokaság szemléletes képe. A fejezet végén azt is megtudjuk, hogy mi is történhetett Alice-szel, amikor átlépett Tükörországba Lewis Caroll meseregényében. Lényegében a fogalmak megismerésén keresztül bejárjuk a felületek osztályozásához vezető út egy részét is.

    

2. A II. rész (Felületek geometriája): Háromféle homogén kétdimenziós geometria létezik, az elliptikus geometria (a gömbfelület geometriája), a hiperbolikus geometria (ne feledjük: Bolyai János teremtette ezt az „új más világot”) és az euklideszi geometria, amelyek mindegyike állandó görbületű. A fejezet első részében a szerző az elliptikus geometria és a hiperbolikus geometria alapfogalmaiba ad betekintést. A felületek lehetséges geometriáit vizsgálva kapjuk, hogy a felületek nagy részén hiperbolikus geometria érvényesül, leszámítva a gömbfelületet és a projektív síkot, amelyekhez az elliptikus geometria tartozik valamint a tóruszt és a Klein-kancsót, amelyeken euklideszi geometria érvényesül. A fejezet utolsó részében a felület globális topológiájának egyik karakterisztikus számáról, az Euler-számról, valamint a felület területének és görbületének az Euler-számmal való kapcsolatáról, azaz a Gauss-Bonnet-képletról van szó.

    

3. A III. rész (Háromsokaságok geometriája): A négydimenziós tér, majd ehhez kapcsolódva a 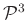projektív tér, valamint a hipergömb, a hiperbolikus tér és a nyalábok szemléletes bemutatása után tér rá a szerző a háromsokaságok geometriáinak ismertetésére. A háromdimenziós elliptikus 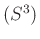, hiperbolikus és euklideszi 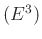geometriák mindegyikéhez találunk a könyvben háromsokaságra példákat, amelyek ezeket a geometriákat hordozzák. Azonban W. Thurston és munkatársai megmutatták, hogy további öt olyan homogén geometria létezik, amely előfordul háromsokaságokon. Ezek a 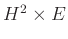, , 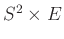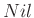(csavart euklideszi), 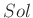, 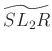(csavart 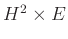) geometria. A tapasztalat azt mutatja, hogy a háromsokaságok nagy része hiperbolikus geomeriájú. A többi háromsokaság pedig a maradék hét geometria valamelyikét hordozza, vagy bizonyos vágásokkal olyan részekre vágható szét, amelyek geometriája az előbb felsorolt nyolc geometria (a Thurston-geometriák) közül kerül ki. (Megjegyzem, hogy könyv megírásakor ez még sejtés volt, a „Thurston Geometrization Conjecture” bitonyítása 2003-ból való, és Grigory Perelman nevéhez fűződik.)

    

4. IV. rész (A Világegyetem): Ebben a fejezetben a világegyetemünk lehetséges geometriai szerkezetének elemzésére kerül sor. A fizikai megfigyelések arra utalnak, hogy a világegyetem homogén és izotróp, így a lehetséges geometriák köre az elliptikus, hiperbolikus és euklideszi geometriákra szűkül. A viágegyetem megfigyelt tágulása pedig a hiperbolikus geometriát valószínűsíti. (Megjegyzem, hogy a világegyetem geometriájának meghatározására már a XIX. században C. F. Gauss és N. I. Lobacsevszkij is tett kísérletet, de természetesen a mérési pontatlanságok miatt esély sem mutatkozott helyes eredményekre.)

    

5. Függelék: Válogatott gyakorlatmegoldásokat és útmutatókat tartalmaz.

    

A könyvet Szilárd Ágnes és Stipsicz András remek fordításában olvashatjuk. Tudom javasolni mindenkinek, aki a téma iránt érdeklődik. Kiemeltem javaslom az érdeklődő középiskolás tanulóknak, akik bizonyos részeket önállóan is fel tudnak dolgozni, de megjegyzem, hogy számukra bizonyos fogalmakhoz és fejezetekhez tanári segítség szükséges. Leginkább mégis a matematikával és fizikával foglalkozó egyetemi hallgatóknak okozhat „heuréka” érzést a könyv tanulmányozása, mert a precíz topológiai és differenciálgeometriai tanulmányok közben megmutatja azok lényeges és szép hátterét, a vizsgált terek „vizualizálásának” lehetőségeit.

Javasolni szeretném még, hogy a téma iránt érdeklődők keressék fel a szerző honlapjait, ahol szinte az általános iskolásoktól (például: Torus Games) kezdve a kutatókig (például: SnapPea) találnak érdekes játékokat illetve programokat, amelyek a könyben leírtakhoz kapcsolódva további információkat tartalmaznak. Elérhetőségeik: http://geometrygames.org/ és http://www.geometrygames.org/SoS/.