A Springer kiadásában 2018-ban megjelent Mathematical Geosciences, Hybrid Symbolic-Numeric Methods c. könyv szerzői: Joseph Awange, Béla Paláncz, Robert H. Lewis és Lajos Völgyesi. A könyv hibrid szimbolikus-numerikus módszereket mutat be.
A könyv bevezetőjében a szerzők néhány példán keresztül mutatják be, hogy mit is jelent egy adott problémát numerikus, illetve szimbolikus módszerrel megoldani. A két módszer erősségeinek és gyengeségeinek összevetése után megmutatják, hogyan lehet a két módszer ötvözésével eredményre jutni.
Hogy bepillantást nyerjünk a hibrid módszerekbe, kövessük a szerzők által kitaposott utat, és lássunk néhány illusztratív példát.
Egy alapvető feladat az alábbi egyenletrendszer összes megoldását meghatározni:
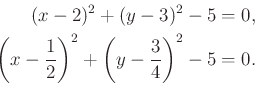
Egy vázlatos rajz után is már látszik, hogy a két kör két pontban metszi egymást, így ezek a metszéspontok az egyenletrendszer megoldásai.
Alapvetően két út áll előttünk, hogy a problémát megoldjuk. Az egyik lehetőség; szimbolikus módszer alkalmazása, vagyis algebrai átalakítások sorozatát végrehajtva kifejezzük az ![]() és
és ![]() ismeretleneket. Egy ilyen szimbolikus módszer lehet egészen egyszerű, mint például a teljes négyzetté alakítás egy másodfokú egyenlet esetében; vagy öszetettebb, mint a fenti példa esetében a Gröbner-bázisok alkalmazása. Az eredeti egyenletrendszer így átalakítható egy speciálalakú egyenletrendszerré, melynek megoldásai megegyeznek az eredeti rendszer megoldásaival:
ismeretleneket. Egy ilyen szimbolikus módszer lehet egészen egyszerű, mint például a teljes négyzetté alakítás egy másodfokú egyenlet esetében; vagy öszetettebb, mint a fenti példa esetében a Gröbner-bázisok alkalmazása. Az eredeti egyenletrendszer így átalakítható egy speciálalakú egyenletrendszerré, melynek megoldásai megegyeznek az eredeti rendszer megoldásaival:
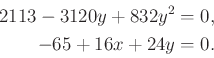
Az első egyenlet megoldásait behelyettesítve a második egyenletbe a metszéspontok egyszerűen meghatározhatók:
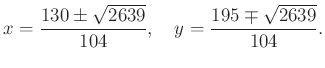
A másik lehetőség, hogy megpróbáljuk fokozatosan közelíteni a megoldásokat. Ez azt jelenti, hogy egy kezdeti ![]() pontból kiindulva aritmetikai műveletek alkalmazásával egy újabb
pontból kiindulva aritmetikai műveletek alkalmazásával egy újabb ![]() pontot kapunk, ezt ismételve egy
pontot kapunk, ezt ismételve egy ![]() pontsorozathoz jutunk. A numerikus módszer akkor sikeres, ha az általa előállított sorozat konvergál az egyik megoldáshoz, így remélhetőleg nem túl sok iteráció után meghatározhatjuk az egyik metszéspont numerikus közelítését.
pontsorozathoz jutunk. A numerikus módszer akkor sikeres, ha az általa előállított sorozat konvergál az egyik megoldáshoz, így remélhetőleg nem túl sok iteráció után meghatározhatjuk az egyik metszéspont numerikus közelítését.
A fenti példa esetében alkalmazhatjuk a Newton-módszert:
amely az alábbi rekurzióhoz vezet:
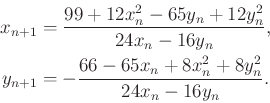
Kiindulva az ![]() és
és ![]() pontból, négy iteráció után az
pontból, négy iteráció után az ![]() és
és ![]() eredményt kapjuk, ami 5 tizedesjegyig megegyezik a pontos megoldással. Ha a másik megoldást is meg szeretnénk találni, egy másik kezdetiértéket kell választanunk. Például egy megfelelő választás az
eredményt kapjuk, ami 5 tizedesjegyig megegyezik a pontos megoldással. Ha a másik megoldást is meg szeretnénk találni, egy másik kezdetiértéket kell választanunk. Például egy megfelelő választás az ![]()
![]() kezdeti érték. Ugyanakkor a rekurzióból jól látható, hogy például a
kezdeti érték. Ugyanakkor a rekurzióból jól látható, hogy például a ![]() pontból nem indíthatjuk az algoritmust. Az algoritmus csak akkor működik megfelelően, ha egyik pont sem esik az
pontból nem indíthatjuk az algoritmust. Az algoritmus csak akkor működik megfelelően, ha egyik pont sem esik az ![]() egyenesre, sőt a numerikus értékek miatt már az is probléma lehet, ha valamelyik lépésben túlságosan megközelítjük ezt az egyenest.
egyenesre, sőt a numerikus értékek miatt már az is probléma lehet, ha valamelyik lépésben túlságosan megközelítjük ezt az egyenest.
Nagy általánosságban megállapítható, hogy egy numerikus módszer:
- Kezdeti értéket igényel, érzékeny a kerekítési hibákra és csak egyetlen megoldást ad.
- Összetett problémák megoldására is alkalmazható, a lépések aritmetikai műveleteket igényelnek, így gépközeli nyelven könnyen implementálható gyorsan futó algoritmus.
Ezzel szemben egy szimbolikus módszer:
- Nem igényel kezdeti értéket, nem érzékeny a kerekítési hibára és egyszerre több megoldást is ad.
- Komplex problémák megoldására kevésbé alkalmazható, a számítási lépések algebrai manipulációkat igényelnek, így az implementációhoz komputeralgebrai rendszer szükséges.
A hibrid módszer ötvözi a szimbolikus és numerikus módszereket. Egy példa lehet a gradiens módszer, amivel az ![]() többváltozós skalárértékű függvényt szeretnénk minimalizálni. A módszerből adódóan az alábbi alakú rekurziót kapjuk:
többváltozós skalárértékű függvényt szeretnénk minimalizálni. A módszerből adódóan az alábbi alakú rekurziót kapjuk:
Tisztán numerikus módszert használva, a gradiens érékét csak közelíteni tudjuk. Ha viszont a gradienst szimbolikusan meghatározzuk, akkor egyrészt megszabadulunk a gradiens közelítése okozta numerikus hibától, másrészt iterációnként jelentősen kevesebb műveletre van szükség a gradiens értékének kiszámításához.
Egy másik példa, a numerikus és szimbolikus módszerek ötvözésére az
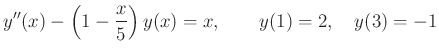
peremérték-feladat megoldása. Új változók bevezetésével a fenti másodrendű egyenlet átalakítható egy elsőrendű rendszerré:

az ![]() és
és ![]() peremfeltétellel. Alkalmazzuk a negyedrendű Runge–Kutta algoritmust az
peremfeltétellel. Alkalmazzuk a negyedrendű Runge–Kutta algoritmust az ![]()
![]() kezdetiérték-problémára. A Runge–Kutta módszer iterációs lépése nem csak numerikus értékek esetén, hanem szimbólumokat tartalmazó kifejezésekre is elvégezhető, bár nem árt hozzá egy olyan számítógépes algebrai rendszer, mint a Wolfram Mathematica. Tíz iterációt elvégezve
kezdetiérték-problémára. A Runge–Kutta módszer iterációs lépése nem csak numerikus értékek esetén, hanem szimbólumokat tartalmazó kifejezésekre is elvégezhető, bár nem árt hozzá egy olyan számítógépes algebrai rendszer, mint a Wolfram Mathematica. Tíz iterációt elvégezve ![]() lépésközzel kapjuk, hogy
lépésközzel kapjuk, hogy
vagyis egy olyan kifejezést, amely tartalmazza a kezdeti értékben szereplő ismeretlen ![]() paramétert. Fölhasználva a peremérték-feltételt,
paramétert. Fölhasználva a peremérték-feltételt, ![]() értéke, és így a megoldás közelítése is kiszámítható.
értéke, és így a megoldás közelítése is kiszámítható.
Miután sikerült megvilágítani hibrid módszerek mibenlétét és hasznosságát, a könyv három fő részre oszlik. Az első rész nemlineáris egyenletrendszerek megoldását tárgyalja, ezen belül is előbb polinomiális rendszerekkel, majd később általánosabb nemlineáris rendszerekkel, illetve túl- és alulhatározott rendszerekkel foglalkozik.
A második rész optimalizációs módszereket mutat be, ezen belül is a „soft computing” megközelítésekkel találkozhatunk, többek között szerepel a szimulált lehűtés, a genetikus algoritmusok és részecskeraj-optimalizáció is.
Végül a könyv harmadik és egyben utolsó része függvények közelítésével és adatok modellezésével foglalkozik. Itt találkozhatunk a radiális bázisfüggvényekkel való közelítéssel, illetve a gépi tanulás témaköréből jól ismert SVM-mel (Support Vector Machine). Szintén érdekes a szimbolikus regressziót tárgyaló fejezet, ahol genetikus algoritmus segítségével próbálnak meg olyan szimbolikus formulát kitalálni, ami aztán jól illeszthető az adatokra. A robusztus regresszió egy szintén fontos téma, ahol például a RANSAC (RANdom SAmple Consensus) algoritmus is szerepel. Ez az algoritmus képes a kiugró értékekkel terhelt adatokra robusztus módon függvényt illeszteni. A sztochasztikus modellezés fejezetben találkozhatunk többek között sztochasztikus differenciálegyenletek numerikus megoldásainak módszereivel és paraméterbecsléssel is. Az utolsó fejezet végül azzal foglalkozik, hogy a hibrid módszerek hogyan használhatják ki a párhuzamos számítást.
A fejezeteket mindig alkalmazások és gyakorló feladatok zárják. Különösen itt érhető tetten a könyv címét is adó földtudomány, hiszen több, a könyvben bemutatott alkalmazás is a földtudományhoz kapcsolódik.
A legtöbb számítást programkódok segítségével követhetjük nyomon. Pontosabban Wolfram Mathematica programkódokat láthatunk, amelyek rendkívül jól olvashatók, még talán a programozásban kevésbé jártasak számára is. Annak pedig, aki gyakorlott használója a Mathematica programnak, kifejezetten élvezetes lehet ezen számítások olvasása. Az ábrák kimagaslóan jó minőségűek, szépek és hasznosak.
Az egész könyv gyakorlati központú, rengeteg példát tartalmaz, ezért bátran ajánlom minden olyan érdeklődő számára, aki nem csak tanulni akar hibrid módszerekről, hanem alkalmazni is akarja azokat.
Csikja Rudolf a BME villamosmérnöki szakán végzett robotika szakterületen, majd a BME TTK doktori iskolában folyatatta tanulmányait matematika PhD képzésen, dinamikai rendszerek témában. A Wolfram Mathematicát több, mint 10 éve használja, a járműdinamika és szabályozás területén algoritmus fejlesztőként dolgozik a Thyssenkrupp Components Technology Hungary Kft-nél.









